3 признака равенства треугольников 7 класс теорема кратко

Треугольники. Признаки равенства треугольников

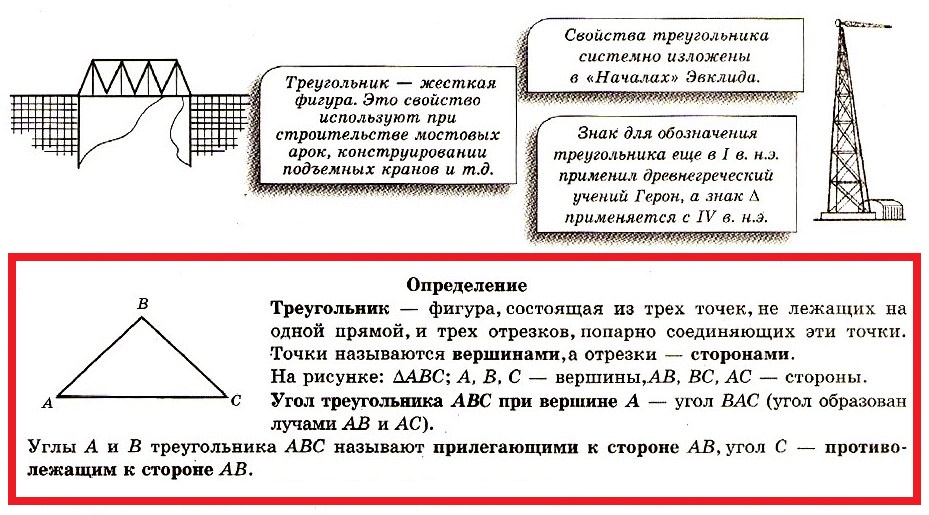
Треугольник − это геометрическая фигура, образованная соединением отрезками трех, не лежащих на одной прямой точек .

Эти точки называются вершинами треугольника. Отрезки, соединяющие эти точки называются сторонами треугольника.

Треугольник обозначается знаком ⊿. Например треугольник ABC обозначается так: ⊿ABC. Этот же треугольник можно обозначать так: ⊿BAC, ⊿CBA и т.д.

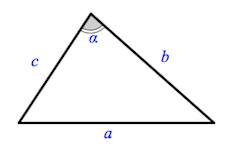
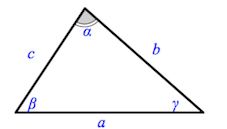
Углы треугольника обозначают так ∠BAC, ∠ABC, ∠BCA. Эти же углы коротко обозначают также ∠A, ∠B, ∠C, соответственно. Углы треугольника принято также обозначать греческими буквами α, β, γ и т.д. Стороны тркеугольника обозначают так AB, BC, AC. Принято также стороны обозначать одной строчной буквой, причем сторона напротив угла A ,обозначается буквой a, сторона напротив угла B− b, сторона напротив угла C− c. Сумма трех сторон треугольника называется периметром треугольника.

Как известно, две треугольники называются равными, если при наложении друг на друга их можно совместить. На Рис.2 представлены два треугольника ABC и A₁B₁C₁. Треугольник ABC можно наложить на треугольник A₁B₁C₁ так, чтобы вершины и стороны этих треугольников попарно совместились. Очевидно, что при этом совместятся и соответствующие углы.

Вышеизложенное можно сформулировать так:

Если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Равенство треугольников ABC и A₁B₁C₁ обозначается так:

Первый признак равенства треугольников

Теорема 1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.

Доказательство. Рассмотрим треугольники ABC и A₁B₁C₁ (Рис.3). Пусть AB=A₁B₁, AС=A₁С₁ и ∠A=∠A₁. Докажем, что .

Так как ∠A=∠A₁, то треугольник ABC можно наложить на треугольник A₁B₁C₁ так, чтобы вершины A и A₁ совпадали, а стороны AB и AС наложились на лучи A₁B₁ и A₁C₁, соответственно.

Так как по условию теоремы AB=A₁B₁, AС=A₁С₁, то сторона AB совместится со стороной A₁B₁, а сторона AС − со стороной A₁С₁.Тогда совместятся B и B₁, C и С₁. Следовательно сторона BC совместится со стороной B₁C₁. То есть треугольники ABC и A₁B₁C₁ полностью совместятся. Теорема доказана.

Второй признак равенства треугольников

Теорема 2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то эти треугольники равны.

Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁ (Рис.4). Пусть AB=A₁B₁, ∠A=∠A₁, ∠B=∠B₁. Докажем, что .

Наложим треугольник ABC на треугольник A₁B₁С₁ так, чтобы вершина A совмещалась с вершиной A₁, сторона AB − со стороной A₁B₁ (по условию теоремы AB=A₁B₁), а вершины C и С₁ оказались по одну сторону от прямой A₁B₁.

Так как ∠A=∠A₁ и ∠B=∠B₁, то сторона AС наложится на луч A₁C₁ а сторона BС − на луч B₁С₁. Тогда вершина C окажется на луче A₁C₁ и на луче B₁C₁. Т.е. она окажется на пересечении этих лучей и, следовательно, вершина C совместится с общей точкой лучей A₁C₁ и B₁C₁, т.е. с вершиной C₁. Таким образом совместятся стороны AC и A₁C₁, BC и B₁C₁. То есть треугольники ABC и A₁B₁С₁ полностью совместятся, поэтому они равны. Теорема доказана.

Третий признак равенства треугольников

Теорема 3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то эти треугольники равны.

Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁. Пусть AB=A₁B₁, AC=A₁C₁ и BC=B₁C₁. Докажем, что . Приложим треугольник ABC к треугольнику A₁B₁С₁ так, чтобы вершина A совмещалась с вершиной A₁, вершина B совмещалась с вершиной B₁, а вершины С и С₁ находились по разные стороны от прямой A₁B₁.

Возможны три варианта: луч CC₁ проходит внутри угла ACB(Рис.6); луч CC₁ совпадает с одной из сторон угла ACB (Рис.7); луч CC₁ проходит вне угла ACB(Рис.8). Рассмотрим эти три случая по отдельности.

Вариант 1 (Рис.6). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольники AСС₁ и BСС₁ равнобедренные. Тогда ∠1=∠2 и ∠3=∠4 и, следовательно:

Имеем AC=A₁C₁, BC=B₁C₁ ∠ACB=∠A₁C₁B₁ и по первому признаку равенства треугольников . Теорема доказана.

Вариант 2 (Рис.7). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольник BСС₁ равнобедренный. Тогда ∠1=∠2. Имеем: AC=A₁C₁, BC=B₁C₁, ∠1=∠2 и по первому признаку равенства треугольников . Теорема доказана.

Вариант 3 (Рис.8). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольники AСС₁ и BСС₁ равнобедренные. Тогда ∠1=∠2 и 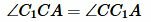и, следовательно:

Имеем AC=A₁C₁, BC=B₁C₁ 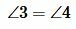и по первому признаку равенства треугольников . Теорема доказана.

Задачи и решения

Задача 1. На сторонах угла CAD отмечены точки B и E так, что точка B лежит на отрезке AC, а точка E − на отрезке AD, причем AC=AD и AB=AE. Докажите, что ∠CBD=∠DEC (Рис.9).

Доказательство. AC=AD, AE=AB, ∠CAD общий для треугольников CAE и DAB. Тогда, по первому признаку равенства треугольников (теорема 1) ⊿ACE=⊿ADB. Следовательно ∠DBA=∠AEC. Поскольку углы CBD и DBA смежные, то CBD=180°−∠DBA. Аналогично CED=180°-∠AEC. То есть ∠CBD=∠DEC. Конец доказательства.

Задача 2. По данным рисунка рис.10 докажите, что OP=OT, ∠P=∠T

Доказательство. OC=OB, ∠TCO=∠PBO=90°. Углы TOC и POB вертикальные (следовательно равны) тогда, повторому признаку равенства треугольников (теорема 2), ⊿TCO=⊿PBO. Конец доказательства.

Краткий конспект учебника по геометрии за 7 класс (А.Г.Мерзляк и др.) в 4-х частях. Цитаты из учебника помогут учащимся, которые сдали учебник в библиотеку при переходе в старший класс, быстро освежить знания, полученные в 7 классе. Часть 2-я.

Перейти к Главе 1
   Перейти к Главе 3
   Перейти к Главе 4

---

---

Глава 2. Треугольники

СОДЕРЖАНИЕ: 7) Равные треугольники. Высота, медиана, биссектриса треугольника. 8) Первый и второй признак равенства треугольников. 9) Равнобедренный треугольник и его свойства. 10) Признаки равнобедренного треугольника. 11) Третий признак равенства треугольников. 12) Теоремы.

§ 7. Равные треугольники. Высота, медиана, биссектриса треугольника

Рассмотрим три точки А, В, С, не лежащие на одной прямой. Соединим их отрезками АВ, ВС, СА. Полученная фигура ограничивает часть плоскости, выделенную на рисунке 108 зеленым цветом. Эту часть плоскости вместе с отрезками АВ, ВС и СА называют треугольником.

Точки А, В, С называют вершинами, а отрезки АВ, ВС, СА — сторонами треугольника. Треугольник называют и обозначают по его вершинам. Треугольник, изображённый на рисунке 108, обозначают так: ΔАВС, или ΔВСА, или ΔАСВ (читают: «треугольник АВС», «треугольник ВСА», «треугольник АСВ»).

Углы ВАС, АВС, ВСА (рис. 109) называют углами треугольника АВС. В треугольнике АВС (рис. 109), например, угол В называют , противолежащим стороне АС, углы А и С — углами, прилежащими к стороне АС, сторону АС — стороной, противолежащей углу В, стороны АВ и АС — сторонами, прилежащими к углу А.

§ 8.  Первый и второй признак равенства треугольников

§ 9. Равнобедренный треугольник и его свойства

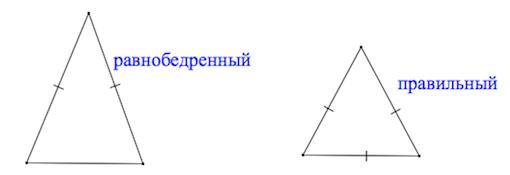
Определение. Треугольник, у которого две стороны равны, называют равнобедренным. 
Равные стороны треугольника называют боковыми сторонами, а третью сторону — основанием равнобедренного треугольника. Вершиной равнобедренного треугольника называют общую точку его боковых сторон. При этом угол В называют углом при вершине, а углы А и С — углами при основании равнобедренного треугольника.

Определение. Треугольник, у которого все стороны равны, называют равносторонним.
Равносторонний треугольник — частный случай равнобедренного треугольника.

§ 10. Признаки равнобедренного треугольника

§ 11. Третий признак равенства треугольников

§ 12. Теоремы

Формулировки всех теорем, которые мы доказали, состоят из двух частей. Первую часть теоремы (то, что дано) называют условием теоремы, вторую часть теоремы (то, что требуется доказать) — заключением.

Например, в теореме 8.1 (первый признак равенства треугольников) условием является то, что две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, а заключением — равенство
ников.

Все знакомые вам теоремы можно условно разделить на теоремы-свойства и теоремы-признаки. Например, теорема 1.1 устанавливает свойство пересекающихся прямых, теорема 9.1 — свойство равнобедренного треугольника.

Теоремы-признаки перечисляют свойства, по которым можно распознать фигуру, т. е. отнести её к тому или иному виду (классу). Так, теоремы-признаки равенства треугольников указывают требования, по которым два треугольника можно причислить к классу равных. Например, в теоремах 10.1-10.4 сформулированы свойства, по которым распознают равнобедренный треугольник.

Теоремы, которые следуют непосредственно из аксиом или теорем, называют теоремами-следствиями или следствиями. Например, свойство углов, противолежащих равным сторонам треугольника, является следствием из теоремы 9.1.
Если в теореме 8.2 о свойстве серединного перпендикуляра поменять местами условие и заключение, то получим теорему 11.2. Такие теоремы называют взаимно обратными. Если какую-то из этих теорем назвать прямой, то вторую теорему будем называть обратной.

Меняя местами условие и заключение теоремы, надо быть очень внимательными: не всегда можно получить истинное утверждение. Например, утверждение, обратное теореме 4.1 о сумме смежных углов, неверно. Действительно, если сумма каких-то двух углов равна 180°, то совершенно не обязательно, чтобы эти углы были смежными.

Вы знаете, что справедливость теоремы устанавливают путём логических рассуждений, т. е. доказательства. Теорема 1.1 была доказана методом от противного. Название этого метода фактически отражает его суть. Мы предположили, что заключение теоремы 1.1 неверно. На основании этого предположения с помощью логических рассуждений был получен факт, который противоречил основному свойству прямой.

Методом от противного также были доказаны и другие теоремы, например теоремы 5.1, 10.3. Очень важно, чтобы доказательство теоремы было полным, т. е. рассмотрены все возможные случаи. Так, полное доказательство теоремы 11.1 (третий признак равенства треугольников) потребовало рассмотрения всех трёх возможных случаев.

Умение видеть все тонкости и нюансы доказательства — важнейшее качество, формирующее математическую культуру. Если бы, например, при доказательстве теоремы 8.2 о свойстве серединного перпендикуляра мы не рассмотрели отдельно случай, когда точка X является серединой отрезка то обращение к треугольникам АХМ и ВХМ было бы не совсем «законным».

При доказательстве теоремы 10.4 (признак равнобедренного треугольника) мы использовали приём дополнительного построения: чертёж дополнили элементами, о которых не шла речь в условии теоремы. Этот метод является ключом к решению многих задач и доказательству ряда теорем. Поэтому очень важно научиться видеть «выгодное» (результативное) дополнительное построение.

ИТОГИ ГЛАВЫ 2.

Определение. Равные фигуры
Две фигуры называют равными, если их можно совместить наложением.

Основное свойство равенства треугольников
Для данного треугольника АВС и луча А₁М существует треугольник A₁B₁C₁ равный треугольнику АВС, такой, что АВ = А₁В₁, ВС = В₁С₁, АС = А₁С₁ и сторона A₁B₁ принадлежит лучу А₁М, а вершина С₁ лежит в заданной полуплоскости относительно прямой А₁М.

ТЕОРЕМА 7.1. О единственности прямой, перпендикулярной данной
Через точку, не принадлежащую данной прямой, проходит только одна прямая, перпендикулярная данной.

Высота треугольника
Перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону, называют высотой треугольника.

Медиана треугольника
Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны, называют медианой треугольника.

Биссектриса треугольника
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противолежащей стороны, называют биссектрисой треугольника.

ТЕОРЕМА 8.1. Первый признак равенства треугольников: по двум сторонам и углу между ними
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Серединный перпендикуляр отрезка
Прямую, перпендикулярную отрезку и проходящую через его середину, называют серединным перпендикуляром отрезка.

ТЕОРЕМА 8.2. 
Каждая точка серединного перпендикуляра отрезка равноудалена от концов этого отрезка.

ТЕОРЕМА 8.3. Второй признак равенства треугольников: по стороне и двум прилежащим к ней углам
Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Равнобедренный треугольник
Треугольник, у которого две стороны равны, называют равнобедренным.

Равносторонний треугольник
Треугольник, у которого все стороны равны, называют равносторонним.

ТЕОРЕМА 9.1. Свойства равнобедренного треугольника
В равнобедренном треугольнике: 1) углы при основании равны; 2) биссектриса треугольника, проведённая из угла при вершине, является медианой и высотой.

Свойства треугольников, следующие из свойств равнобедренного треугольника
• В треугольнике против равных сторон лежат равные углы.
• В равнобедренном треугольнике биссектриса, высота и медиана, проведённые из его вершины, совпадают.
• В равностороннем треугольнике все углы равны.
• В равностороннем треугольнике биссектриса, высота и медиана, проведённые из одной вершины, совпадают.

Признаки равнобедренного треугольника
• Если медиана треугольника является его высотой, то этот треугольник равнобедренный (Теорема 10.1)
• Если биссектриса треугольника является его высотой, то этот треугольник равнобедренный (Теорема 10.2)
• Если в треугольнике два угла равны, то этот треугольник равнобедренный (Теорема 10.3)
• Если медиана треугольника является его биссектрисой, то этот треугольник равнобедренный (Теорема 10.4)

ТЕОРЕМА 11.1.Третий признак равенства треугольников: по трём сторонам
Если три стороны одного треугольника равны соответственно трём сторонам другого треугольника, то такие треугольники равны.

---

Это конспект по теме «Мерзляк Геометрия 7 Глава 2». Выберите дальнейшие действия:

• Перейти Главе 1 «Простейшие геометрические фигуры»
• Перейти Главе 3 «Параллельные прямые. Сумма углов треугольника»
• Перейти Главе 4 «Окружность и круг. Геометрические построения»
• Вернуться к Списку конспектов по геометрии

Признаки равенства треугольников

• Первый признак равенства треугольников
• Второй признак равенства треугольников
• Третий признак равенства треугольников
• Признаки равенства прямоугольных треугольников

Два треугольника считаются равными, если их можно совместить наложением. Но, чтобы не выполнять каждый раз наложение, для доказательства равенства треугольников, установили три признака, по которым можно определить, совместятся треугольники или нет. Эти признаки называются признаками равенства треугольников.

Первый признак равенства треугольников

Теорема:

Два треугольника равны, если у них равны две стороны и угол, лежащий между этими сторонами.

Доказательство:

Рассмотрим два треугольника  ABC  и  A₁B₁C₁,  у которых:

 AB = A₁B₁,  AC = A₁C₁,  ∠A = ∠A₁.

Требуется доказать, что

ABC = A₁B₁C₁.

Если наложить  A₁B₁C₁  на  ABC  так, чтобы точка  A₁  совместилась с точкой  A  и сторона  A₁B₁  совместилась со стороной  AB,  то точка  B  совместится с точкой  B₁,  так как  A₁B₁ = AB.  Сторона  A₁C₁  совместится со стороной  AC,  так как  ∠A = ∠A₁.  Точка  C₁  совпадёт с точкой  C,  так как  A₁C₁ = AC.  Стороны  B₁C₁  и  BC  совместятся, так как совместились их концы. Таким образом, треугольники совместятся. Теорема доказана.

Второй признак равенства треугольников

Теорема:

Два треугольника равны, если у них равна одна из сторон и два прилежащих к ней угла.

Доказательство:

Рассмотрим два треугольника  ABC  и  A₁B₁C₁,  у которых:

 AC = A₁C₁,  ∠A = ∠A₁  и  ∠C = ∠C₁.

Требуется доказать, что

ABC = A₁B₁C₁.

Если наложить  A₁B₁C₁  на  ABC  так, чтобы точка  A₁  совместилась с точкой  A  и сторона  A₁C₁  совместилась со стороной  AC,  то точка  C₁  совпадёт с точкой  C,  так как  A₁C₁ = AC.  Сторона  A₁B₁  совпадёт со стороной  AB,  так как  ∠A = ∠A₁.  Сторона  C₁B₁  совпадёт со стороной  CB, так как  ∠C = ∠C₁.  Вершина  B₁  совпадёт с вершиной  B,  так как  B  и  B₁  будут служить точками пересечения одних и тех же отрезков. Таким образом, треугольники совместятся. Теорема доказана.

Третий признак равенства треугольников

Теорема:

Два треугольника равны, если три стороны одного треугольника равны трём сторонам другого.

Доказательство:

Рассмотрим два треугольника  ABC  и  A₁B₁C₁,  у которых:

AB = A₁B₁,  BC = B₁C₁,  AC = A₁C₁.

Требуется доказать, что

ABC = A₁B₁C₁.

Приложим треугольники  ABC  и  A₁B₁C₁  один к другому так, чтобы вершина  A  совместилась с  A₁,  вершина  C  — с  C₁, а вершины  B  и  B₁  оказались по разные стороны от прямой  AC.

Соединив точки  B  и  B₁,  получим два равнобедренных треугольника  BAB₁  и  BСB₁.

В треугольнике  BAB₁  ∠1 = ∠4,  в  BСB₁  ∠2 = ∠3  (как углы при основании). Следовательно,

∠1 + ∠2 = ∠4 + ∠3,  поэтому  ∠ABC = ∠AB₁C.

Итак,  AB = A₁B₁,  BC = B₁C₁,  ∠ABC = ∠A₁B₁C₁.

Из этого следует, что треугольники  ABC  и  A₁B₁C₁  равны по первому признаку равенства треугольников. Теорема доказана.

Признаки равенства прямоугольных треугольников

Для прямоугольных треугольников, кроме перечисленных трёх признаков равенства, имеются ещё дополнительные признаки, так как у них у всех есть прямой угол, а все прямые углы равны между собой.

Два прямоугольных треугольника будут равны в следующих четырёх случаях:

1. Если катеты одного треугольника равны катетам другого.
2. Если катет и прилежащий к нему острый угол одного треугольника равны катету и прилежащему к нему острому углу другого.
3. Если гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого.
4. Если гипотенуза и катет одного треугольника равны гипотенузе и катету другого.

Признаки равенства треугольников

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.

Давайте рассмотрим три признака равенства треугольников.

Теорема 1. Равенство треугольников по двум сторонам и углу между ними.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

При наложении △A₁B₁C₁ на △ABC вершина A₁ совмещается с вершиной A, и сторона A₁B₁ накладывается на сторону AB, AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

Второй признак равенства треугольников

Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Третий признак равенства треугольников

Теорема 3. Равенство треугольников по трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.

Источник

Что такое равенство треугольников

Треугольник — фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Точки называются вершинами, а отрезки — сторонами.

Треугoльник — жесткая фигура. Это свойство используют при строительстве мостовых арок, конструировании подъемных кранов и т.д. Свойства треугольника системно изложены в «Началах» Эвклида. Знак для обозначения треугольника еще в I в. н.э. применил древнегреческий учений Герон, а знак Δ применяется с IV в. н.э.

Медиана, биссектриса и высота треугольника

Равные треугольники

Аксиома существования треугольника, равного данному.
Каким бы ни был треугольник, существует треугольник, равный ему в заданном расположении относительно данной полупрямой.

Свойства равных треугольников
1. В равных треугольниках соответствующие стороны равны.
2. В равных треугольниках соответствующие углы равны.
3. Периметры равных треугольников равны.
4. Площади равных треугольников равны.
5. Против равных сторон лежат равные углы.
6. Против равных углов лежат равные стороны.

Признаки равенства треугольников

Дополнительные признаки равенства
• Если две стороны и медиана, проведенная к третьей стороне треугольника, соответственно равны двум сторонам и медиане, проведенной к третьей стороне другого треугольника, такие треугольники равны.
• Если два угла и высота,проведенная к стороне, к которой прилегают эти углы, одного треугольника, соответственно равны двум углам и высоте, проведенной к стороне, к которой прилегают эти углы, другого треугольника, то такие треугольники равны.
• Если сторона, высота и медиана, проведенные к стороне одного треугольника, соответственно равны стороне, высоте и медиане, проведенным к этой стороне другого треугольника, то эти треугольники равны.
• Если медиана и углы, на которые она делит угол, одного треугольника, соответственно равны медиане и углам,на которые она делит угол, другого треугольника, эти треугольники равны.

Это конспект по теме «Треугoльник. Равенство треугольников». Выберите дальнейшие действия:

Источник

Треугольник

Треугольник произвольный

Треугольник – это многоугольник с тремя сторонами (тремя углами).

Виды треугольников :+ показать

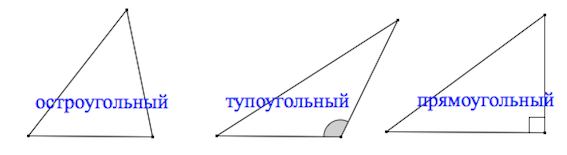
Остроугольный треугольник – треугольник, у которого все углы острые (то есть меньше 90˚).

Тупоугольный треугольник – треугольник, у которого один из углов тупой (больше 90˚).

Прямоугольный треугольник – треугольник, у которого один из углов прямой (равен 90˚).

Равносторонний (правильный) треугольник – треугольник, у которого все три стороны равны.

Свойства

1. Против большей стороны лежит больший угол, и наоборот.

2. Против равных сторон лежат равные углы, и наоборот.

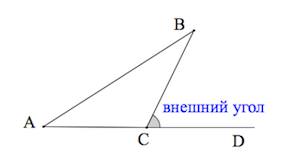
4. Внешний угол треугольника равен сумме внутренних углов,
не смежных с ним:

(Внешний угол образуется в результате продолжения одной из сторон треугольника).

5. Любая сторона треугольника меньше суммы двух других сторон.

Признаки равенства треугольников

1. Треугольники равны, если у них соответственно равны две стороны и угол между ними.

3. Треугольники равны, если у них соответственно равны три стороны.

Биссектриса, высота, медиана

Здесь подробно о биссектрисе, высоте, медиане треугольника.

Средняя линия треугольника

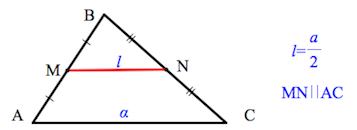
Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.

Средняя линия треугольника параллельна третьей стороне и равна ее половине.

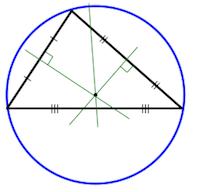
Вписанная окружность

Центр вписанной окружности – точка пересечения биссектрис треугольника.

Описанная окружность

Центр описанной окружности – точка пересечения серединных перпендикуляров.

Соотношение сторон в произвольном треугольнике

Теорема косинусов:

Теорема синусов:

Площадь треугольника

Через сторону и высоту

Через две стороны и угол между ними

Через радиус описанной окружности

Через радиус вписанной окружности

, где – полупериметр

, где – полупериметр

Смотрите также площадь треугольника здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Есть пара ошибок в формулах. В частности в формуле вычисления площади через 2 стороны и угол между ними, в теореме Синусов, в разделе “свойства”.
А вообще отличные статьи, очень выручают, всё понятно и доступно, премного благодарен 😉

Анатолий, спасибо!
В разделе “свойства” ошибок не нашла…
В теореме синусов, – да… не пропечаталась буква гамма. Подправила.
В формуле площади треугольника, вы правы – картинка не соответствовала формуле. Исправила.
К сожалению, ошибки сразу не всегда замечаются.
Благодарю еще раз!

В разделе свойства:

Да, не хватало значка «» у А. Спасибо! 😉

Здраствуйте! Мне нужна ваша помощь!
Задача: ВЕРШИНЫ ТРЕУГОЛЬНИКА ДЕЛЯТ ОПИСАННУЮ ОКОЛО НЕГО ОКРУЖНОСТЬ НА ТРИ ДУГИ, ДЛИНЫ КОТОРЫХ ОТНОСЯТСЯ КАК 6:7:33. НАЙДИТЕ РАДИУС ОКРУЖНОСТИ, ЕСЛИ МЕНЬШАЯ ИЗ СТОРОН РАВНА 11.

Подозреваю, у вас опечатка в условии…
Если длины дуг (а значит и их градусные меры) находятся в отношении , то выходим на уравнение Откуда Значит угол треугольника, что напротив меньшей стороны, есть
Применяем теорему синусов: , откуда

спасибо я так и думал а то не могу решить и всё
СПАСИБО!

Здравствуйте. Пожалуйста, объясните, как решить задачу:
Вписанная в теругольник ABC окружность касается сторон AB, BC и AC в точках K,L и М соответственно.Найдите KL, если AM=2, МС=3 и угол С=π/3

Очевидно,
Примите за .
Примените к треугольнику теорему косинусов:

Найдете , далее можно найти угол и из треугольника найти

Спасибо большое за ваш сайт. Очень радует, тот факт, что когда люди не понимают какую-нибудь задачу, вы помогаете решить. Спасибо. Побольше бы таких сайтов, всё понятно и доступно

Источник

Равные треугольники

Всего получено оценок: 302.

Всего получено оценок: 302.

Изучая тему треугольников, стоит обратить внимание на признаки равенства двух фигур. Их можно использовать во время решений различных заданий. О том, как определить признаки и свойства равенства треугольников – поговорим в этой статье.

Определение

Исходя из определения равных треугольников, в равных треугольниках все соотвествующие стороны равны и все соответствующие углы равны. Используем это свойство для доказательства признаков равенства треугольников способом наложения.

Математик Фалес, чтобы вычесть расстояние от корабля до суши построил треугольник на суше равный треугольнику на «море». Он, таким образом, узнал точное расстояние.

Признаки равенства

Выделяют три признака равенства треугольников:

1. Если две стороны и угол между ними одного треугольника равны соответствующим двум сторонам и углу между ними другого треугольника, то такие фигуры равны.

Рис. 1. Первый признак равенства

2. Если сторона и два прилегающих к ней угла одного треугольника равны соответствующей стороне и двум прилегающим к ней углам другого треугольника, то такие фигуры равны.

Рис. 2. Второй признак равенства

3. Если три стороны в одном треугольнике равны трем сторонам в другом треугольнике, то такие треугольники равны.

Кроме того, стоит выделить некоторые свойства:

Алгоритм доказательства равенства фигур

Порядок названия вершин одного треугольника должен быть одинаковым с порядком названия вершин другого треугольника.

Стойки стремянки могут свободно раздвигаться, до того момента, когда их не зафиксировали перемычкой. Жесткость такой конструкции основывается на третьем признаке равенства фигур.

Пример

Решение:
Стоит обратить внимание на рисунок

Рис. 3. Два треугольника

Что мы узнали?

Для того, чтобы доказать равенство фигур необходимо использовать один из трех признаков равенства треугольников. Треугольники могут быть равными по двум сторонами и углу между ними, по стороне и двум прилегающим к ней углам, а также по трем сторонам.

Источник

Геометрия. 7 класс

Конспект урока

Повторение. Треугольник. Равенство треугольников

Перечень вопросов, рассматриваемых в теме:

Треугольник – это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.

Сумма углов треугольника равна 180°.

Признаки равенства треугольников.

1 признак. Если две стороны и угол между ними одного
треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

2 признак. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

3 признак. Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.

1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Теоретический материал для самостоятельного изучения

Треугольник – это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.

В любом треугольнике:

Два треугольника называются равными, если их можно совместить наложением.

На рисунке изображены равные треугольники ABC и А₁В₁С₁. Каждый из этих треугольников можно наложить на другой так, что они полностью совместятся, т. е. попарно совместятся их вершины, стороны и углы.

Первый признак равенства треугольников:

По двум сторонам и угол между ними.

Второй признак равенства треугольников:

По стороне и двум прилежащим к ней углам.

Третий признак равенства треугольников:

Признаки равенства прямоугольных треугольников.

Свойства прямоугольных треугольников.

Разбор решения заданий тренировочного модуля.

Решение задач по теме: «Прямоугольный треугольник».

Дано: ∠C = 44°.Найдите: ∠ABD.

Помним, что сумма острых углов равна 90°. Равные углы отмечены на рисунке. ∠ABD = 44°.

Дано: AB = 6. Найдите: AC.

Указания к решению: помним, что против угла 30° лежит катет, равный половине гипотенузы. На рисунке найдите три треугольника, в каждом из которых, есть угол 30°.

В треугольнике ABC против угла С = 30°, лежит катет AB = ½AC. Значит, AC = 12.

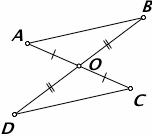
Задача 3. В ∆АВС: ∠А = 30°, ∠В = 80°. Биссектрисы углов А и С пересекаются в точке О. Найти величину ∠АОВ.

Сумма углов А и В равна 110°. Сумма их половинок равна 55°. Тогда: ∠АОВ = 180° – 55° = 125°.

Может ли существовать треугольник со сторонами: 14 см, 17 см, 10 см?

Источник