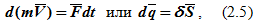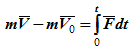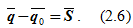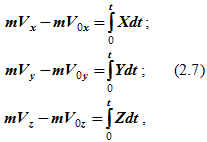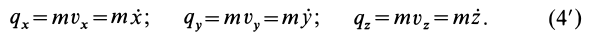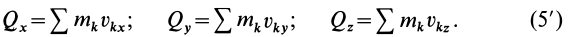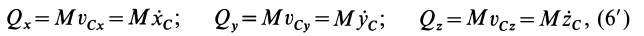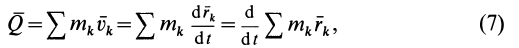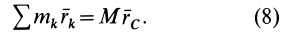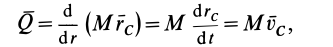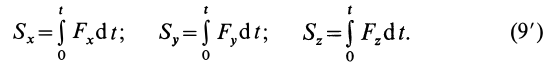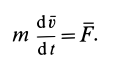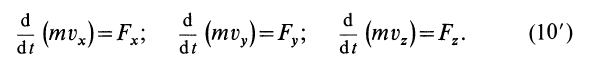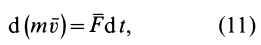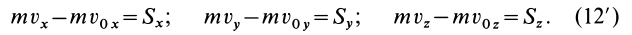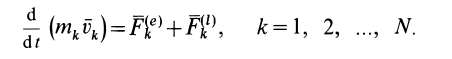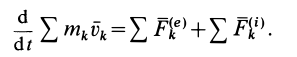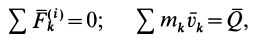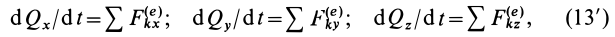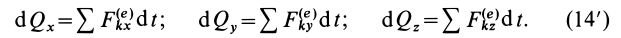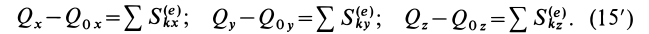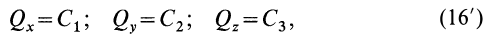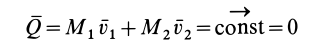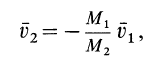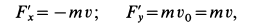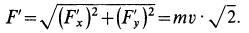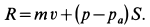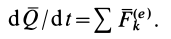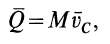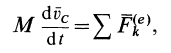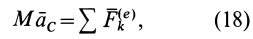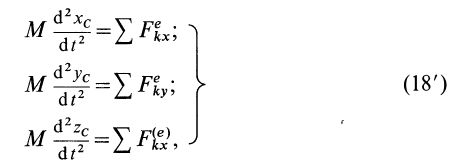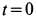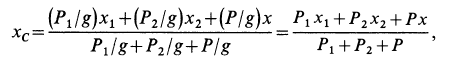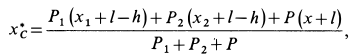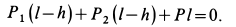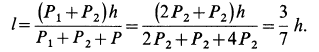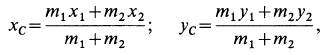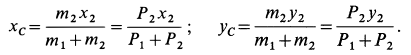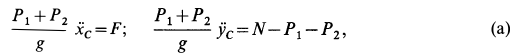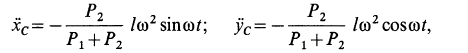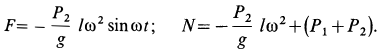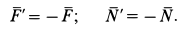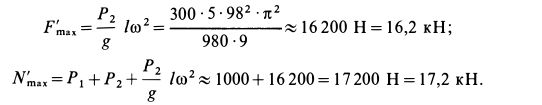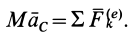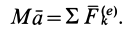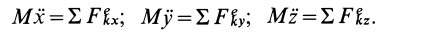1. Теорема в
дифференциальной форме.
Производная
по времени от количества движения
материальной точки равна геометрической
сумме сил, действующих на точку.
Доказательство.
Запишем
основной закон динамики в виде
,
;
(3.17)
2. Теорема в
интегральной (конечной) форме.
Изменение
количества движения материальной точки
за некоторый промежуток времени
равно геометрической сумме импульсов
сил, действующих на точку, за тот же
промежуток времени.
Доказательство.
(3.18)
Векторные
равенства (3.17) и (3.18) можно записать в
проекциях на оси декартовых координат:
,
,
(3.19)
,
(3.20)
При
решении
задач уравнения (3.19) следует применять
в тех случаях,
когда на точку кроме постоянных сил
действуют переменные
силы, зависящие от скорости точки.
П
ример
4.
Т
Рисунок 6
очка массы
движется горизонтально под действием
силы
в среде, сопротивление которой определяется
силой
,
где
.
Какую скорость приобретет точка за
время
,
если движение началось без начальной
скорости?
Решение.
Применим
теорему об
изменении материальной точки
в дифференциальной форме в
проекции на ось
.
Покажем
силы
и
(рис.
6).
;
.
Ответ.
Уравнения
(3.20) позволяют косвенным путем определить
импульс
сил, не зная ни сил, ни времени их действия,
если при
этом начальная и конечная скорости
точки известны.
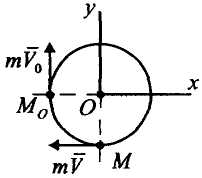
Пример
5.
М
атериальная
точка массы
движется по окружности
с постоянной скоростью
из точки
(рис. 7, а).
Определить
импульс сил, действующих
на точку, за время, в течение которого
точка пройдет — длины окружности.
Р
Рисунок 7, а, б
ешение. Применим
теорему об изменении
количества движения материальной
точки в интегральной форме
.
Найдем
проекции импульса
на оси
координат
(рис. 7, б):
;
.
Импульс
сил
.
Ответ.
.
3.5. Теорема об изменении главного вектора количества движения механической системы
1.
Теорема
в дифференциальной форме
Производная
по
времени от главного вектора количеств
движения
механической системы равна геометрической
сумме
внешних сил, действующих на эту систему.
Доказательство.
На
любую
точку механической системы
действуют силы
и
.
Для
этой точки в соответствии с
(3.17)
.
Для всей системы
,
(3.21)
где
;
.
В
проекциях на оси декартовых координат
(3.21) имеет вид
;
,
.
(3.22)
Следствия из
теоремы:
-
Если
,
то
. -
Если
проекция главного вектора на какую-либо
ось равна
нулю, то проекция количества движения
на эту ось есть
величина постоянная. Например,
,
то
.
2. Теорема в
интегральной (конечной) форме.
Изменение
количества
движения механической системы за
некоторый промежуток времени равно
геометрической сумме
импульсов всех внешних сил, действующих
на точки механической
системы, за тот же промежуток времени.
Доказательство.
(3.23)
где
— импульс
главного вектора внешних сил.
Векторному
равенству (3.23) соответствуют три равенства
в скалярной форме
,
,
(3.24)
Следствия из
теоремы.
-
Если
,
то
. -
Если
,
то
П
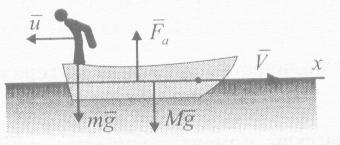
ример
6.
Л
Рисунок 8
одка массы
,
на корме которой стоял человек массы
,
двигалась со
скоростью
.
Затем человек
спрыгнул с
лодки со скоростью
против ее движения.
С какой скоростью
после этого
будет двигаться лодка?
Решение.
Внешними
силами являются вес лодки
,
вес
человека
и
выталкивающая сила
,
(рис. 8). Силой сопротивления
движению пренебрегаем. Все силы
перпендикулярны оси
.
Поэтому
.
.
Ответ.
3.6.
Момент количества движения материальной
точки
относительно
центра и оси
1.
Алгебраический момент
количества движения относительно
центра.
,
.
Правило
знаков:
— при движении точки против хода часовой
стрелки;
—
то же по ходу часовой стрелки.
Алгебраический
момент количества движения материальной
точки
относительно некоторого центра
— скалярная величина, взятая со знаком
или
и равная произведению модуля количества
движения
на расстояние
(перпендикуляр) от этого центра до линии,
вдоль которой направлен вектор
:
(3.25)
2
.
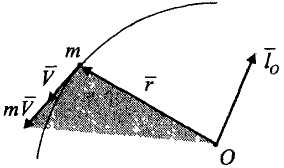
Векторный момент количества движения
относительно центра (рис.
9).
В
Рисунок 9
екторный момент количества движения
материальной точки относительно
некоторого центра
— вектор, приложенный в этом центре и
направленный перпендикулярно плоскости
векторов
и
в ту сторону, откуда движение точки
видно против хода часовой стрелки.
Это определение
удовлетворяет векторному равенству
(3.26)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Так как интеграл от 


Стоящие справа интегралы, как следует из формулы (30), представляют собой импульсы действующих сил. Поэтому окончательно будет

Уравнение (33) выражает теорему об изменении количества движения точки в конечном виде: изменение количества движения точки за некоторый промежуток времени равно сумме импульсов всех действующих на точку сил за тот же промежуток времени.
При решении задач вместо векторного уравнения (33) часто пользуются уравнениями в проекциях. Проектируя обе части равенства (33) на координатные оси, получим

В случае прямолинейного движения, происходящего вдоль оси 
Решение задач. Уравнения (33) или (34) позволяют, зная как при движении точки изменяется ее скорость, определить импульс действующих сил (первая задача динамики) или, зная импульсы действующих сил, определить, как изменяется при движении скорость точки (вторая задача динамики). При решении второй задачи, когда заданы силы, надо вычислить их импульсы, Как видно из равенств (30) или (31), это можно сделать лишь тогда, когда силы постоянны или зависят только от времени.
Таким образом, уравнения (33), (34) можно непосредственно использовать для решения второй задачи динамики, когда в задаче в число данных и искомых величин входят: действующие силы, время движения точки и ее начальная и конечная скорости (т. е. величины 
Задача 95. Точка, масса которой 


Решение. По теореме об изменении количества движения 

Но по условиям задачи 

Для аналитического подсчета можно, используя первые два из уравнений (34), найти

Задача 96. Грузу, имеющему массу 


Рис. 222

Рис. 223
Решение. По данным задачи видно, что для определения времени движения можно воспользоваться доказанной теоремой. Изображаем груз в произвольном положении (рис. 223). На него действуют сила тяжести Р, реакция плоскости N и тормозящая сила F. Направляя ось 

В данном случае 






Таким образом, время торможения растет пропорционально начальной скорости.
Решим эту же задачу, считая, что тормозящая сила равна Q и не постоянна, а с момента начала торможения растет пропорционально времени, т. е. 



Тогда уравнение (а) дает 


Следовательро, в этом случае время торможения удваивается,
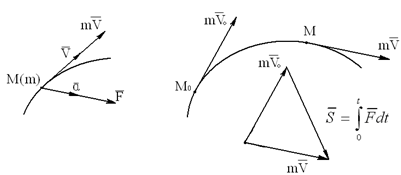
Рассмотрим теорему об изменении количества движения материальной точки в дифференциальной форме
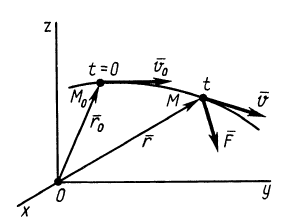
Пусть материальная точка M массы m движется под действием силы F, имея в данный момент скорость V (рисунок 2.1, а).
а б
Рисунок 2.1
Построим вектор количества движения q = m×v.
По второму закону динамики для свободной материальной точки имеем
m×a = F (2.1)
Так как масса материальной точки m – величина постоянная, а ускорение
a = dV/dt, (2.2)
то равенство (2.1) можно представить в виде
d(m×V)/dt = F (2.3)
Выражение (2.3) является формой основного закона динамики (2.1). Первоначально он был записан Ньютоном именно в подобной форме. Формула (2.3) представляет собой содержание теоремы об изменении количества движения материальной точки в дифференциальной форме (в векторном выражении): производная по времени от количества движения материальной точки равна силе, действующей на эту точку.
Проецируя векторное равенство (2.3) на декартовы оси координат, получаем равенства, определяющие содержание теоремы в скалярном виде:
d(m∙Vx)/dt = X;
d(m∙Vy)/dt = Y;
d(m∙Vz)/dt = Z, (2.4)
т.е. производная по времени от проекции количества движения материальной точки на какую-либо ось равна проекции на эту же ось действующей на точку силы.
Умножив обе части равенства (2.3) на элементарный промежуток времени dt, получим выражение теоремы об изменении количества движения материальной точки в другой дифференциальной форме:
где S — импульс силы,
т.е. дифференциал количества движения материальной точки равен элементарному импульсу силы, действующей на эту точку.
Пусть движущаяся материальная точка в начальный момент t=0 находилась в положении M0 и имела скорость V0, а в момент t приходит в положение M и имеет скорость V (рисунок 2.1, б). Тогда, проинтегрировав равенство (2.5) в пределах соответствующего перемещения точки (из положения M0 в положение M), получим
или
Полученное равенство (2.6) представляет собой теорему об изменении количества движения материальной точки в конечной (интегральной) форме (в векторном выражении): изменение количества движения материальной точки за конечный промежуток времени равно полному импульсу действующей на эту точку силы за тот же промежуток времени.
Теорема об изменении количества движения выражает, таким образом, тесную связь, которая имеет место между импульсом силы как меры ее действия во времени и количеством движения как меры механического движения.
Проецируя равенство (2.6) на декартовые оси координат:
получаем выражения (2.7) для теоремы об изменении проекции количества движения в конечной форме (в скалярном выражении): изменение проекции количества движения материальной точки на какую-либо ось за конечный промежуток времени равно проекции на эту же ось полного импульса действующей на точку силы за тот же промежуток времени.
Уравнения в проекциях (2.7) чаще всего применяются при решении задач динамики точки на изменение количества движения.
Рассмотрим следствия теоремы:
- если F=0, то m×V=C=const, или m×V=m×V0 — имеем закон сохранения количества движения.
- если X=0 (F≠0), то m∙Vx = C, или m∙Vx = m∙V0x — имеем закон сохранения проекции количества движения на ось.
То есть если на материальную точку не действует какая-либо сила (проекция действующей силы на какую-либо ось равна нулю), то вектор количества движения точки (проекция количества движения точки на эту же ось) со временем не изменяется.
Примеры решения задач >
Теорема об изменении количества движения механической системы >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Содержание:
Количество движения точки и системы:
Одной из мер движения точки или системы является количество их движения.
Количеством движения материальной точки
Количество движения точки в физике часто называют импульсом материальной точки.
Проекции количества движения точки на прямоугольные декартовы оси координат:
Размерность количества движений в СИ — 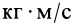
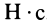
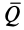
и, следовательно, проекции количества движения системы на прямоугольные декартовы оси координат
Вектор количества движения системы 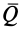
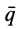
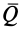
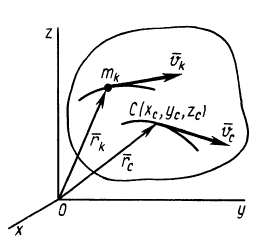
Вычисление количества движения системы
Количество движения системы можно выразить через массу системы 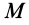
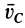
В проекциях на прямоугольные декартовы оси соответственно
где 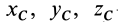
где 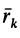
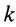
Рис. 40
По формуле для радиуса-вектора центра масс,
Подставляя значение статического момента массы (8) в (7), имеем
так как масса системы 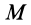
Элементарный и полный импульсы силы
Действие силы 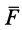
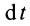
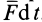
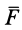
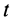
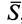
Проекции импульса силы на прямоугольные оси координат выражаются формулами
Единица импульса силы — 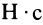
Теорема об изменении количества движения точки
Дифференциальное уравнение движения материальной точки под действием силы 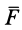
Так как масса точки 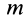
Формула (10) выражает теорему об изменении количества движения точки в дифференциальной форме: первая производная по времени от количества движения точки равна действующей на точку силе.
В проекциях на координатные оси (10) можно представить в виде
Рис. 41
Если обе части (10) умножить на 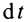
т. е. дифференциал от количества движения точки равен элементарному импульсу силы, действующей на точку.
Проецируя обе части (11) на координатные оси, получаем
Интегрируя обе части (11) в пределах от нуля до 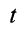
где 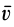
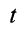
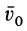
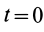
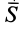
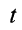
Выражение в форме (12) часто называют теоремой импульсов в конечной (или интегральной) форме: изменение количества движения точки за какой-либо промежуток времени равно импульсу силы за тот же промежуток времени. В проекциях на координатные оси эту теорему можно представить в следующем виде:
Для материальной точки теорема об изменении количества движения в любой из форм, по существу, не отличается от дифференциальных уравнений движения точки.
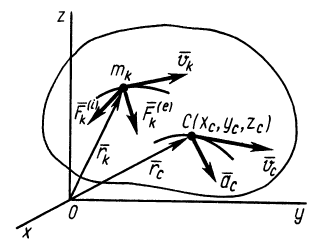
Теорема об изменении количества движения системы
Аналогично тому, как для одной материальной точки, выведем теорему об изменении количества движения для системы в различных формах. Пусть к точкам системы приложены внешняя и внутренняя силы. Тогда для каждой точки можно применить теорему об изменении количества движения, например в форме (10) (см. рис. 40):
Суммируя по всем точкам системы правые и левые части этих соотношений и учитывая, что сумма производных равна производной от суммы, получаем
Так как, по свойству внутренних сил и определению количества движения системы,
то приведенное соотношение можно представить в виде
Выражение (13) является теоремой об изменении количества движения системы в дифференциальной форме: производная по времени от количества движения системы равна векторной сумме всех внешних сил, действующих на систему. В проекциях на прямоугольные декартовы оси координат
т. е. производная по времени от проекции количества движения системы на какую-либо координатную ось равна сумме проекций всех внешних сил системы на ту же ось.
Умножая обе части (13) на 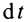
т. е. дифференциал количества движения системы равен векторной сумме элементарных импульсов всех внешних сил, действующих на систему. В проекциях на координатные оси эта теорема примет вид
Вычисляя интегралы от обеих частей (14) по времени- от нуля до получаем теорему импульсов для системы в конечной или интегральной форме:
где 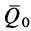
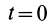
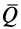
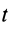
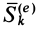
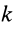
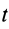
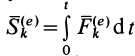
Теорема импульсов для системы в конечной форме формулируется так: изменение количества движения системы за какое-либо время равно векторной сумме всех импульсов внешних сил, действующих на систему за то же время. В проекциях на прямоугольные оси согласно (15) имеем:
Внутренние силы системы не входят явно в теорему об изменении количества движения системы в любой из форм и, следовательно, не влияют непосредственно на изменение количества движения системы. Они могут влиять на изменение количества движения только неявно через внешние силы.
Из теоремы об изменении количества движения для точки и системы при некоторых условиях для внешних сил можно получить так называемые первые интегралы системы дифференциальных уравнений точки и системы. Эти первые интегралы называют законами сохранения количества движения или проекции количества движения на ось. Рассмотрим эти законы сохранения для точки и системы одновременно, считая материальную точку механической системой, состоящей из одной точки.
Законы сохранения количества движения
Законы сохранения количества движения системы получаются как частные случаи теоремы об изменении количества движения для системы в зависимости от особенностей системы внешних сил, приложенных к рассматриваемой механической системе, а для одной точки — от особенностей сил, действующих на точку. Внутренние силы при этом могут быть любыми, так как они явно не влияют на изменение количества движения системы.
Возможны два частных случая.
1. Если векторная сумма всех внешних сил, приложенных к системе, равна нулю, т. е. 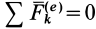
Этот закон (точнее, частный случай теоремы) формулируется так: если главный вектор внешних сил системы равен нулю, то количество движения системы постоянно по величине и направлению. В проекциях на координатные оси, по этому закону,
где 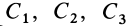
В соотношения (16) и (16′) входят производные от координат точек по времени не выше первого порядка и не входят вторые производные от этих координат. Следовательно, эти соотношения являются первыми интегралами дифференциальных уравнений системы (3).
2. Если равна нулю проекция главного вектора внешних сил на какую-либо координатную ось 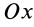
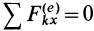
Выражение (17) является законом сохранения проекции количества движения системы: если проекция главного вектора всех внешних сил системы на какую-либо ось равна нулю, то проекция количества движения на ту же ось является постоянной величиной.
Применим закон сохранения количества движения системы для объяснения принципа реактивного движения. Пусть, например, система состоит из двух сочлененных твердых тел, находящихся в покое и свободных от действия внешних сил. Тогда для рассматриваемой системы количество движения все время постоянно и равно нулю. Допустим, что при взрыве пиропатрона (действие внутренних сил) первому телу массой 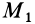
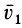
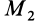
Следовательно,
т. е. второе тело движется в сторону, противоположную первому телу. Если его движению препятствует какая-либо связь, то рассматриваемое тело давит на эту связь с некоторой силой по направлению скорости 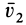
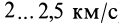
Теорему об изменении количества движения в той или другой форме удобно применять для решения задач именно в рассмотренных частных случаях, хотя в некоторых случаях ее применяют и в общем случае. Отметим, что внутренние силы не влияют на изменение количества движения в изолированных системах, т. е. в системах, которые не соприкасаются с другими телами, не принадлежащими к рассматриваемой системе, или окружающей систему материальной средой.
В неизолированных механических системах внутренние силы, вызывая движение отдельных частей системы вследствие взаимодействия с внешними телами или окружающей материальной средой, могут вызвать внешние силы в виде сил реакций связей или изменения активных сил, которые могут изменить количество движения системы.
Количество движения системы может зависеть от внутренних сил только неявно, через внешние силы.
Рис. 42
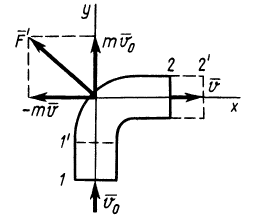
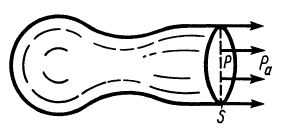
Пример №1
Через изогнутую под прямым углом трубу постоянного сечения за 1 с протекает жидкость массой 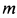
Решение:
Применим к объему жидкости, заключенному между стенками трубы и поперечными сечениями 1 и 2, теорему об изменении количества движения в форме теоремы импульсов за промежуток времени, равный 1 с. За секунду точки жидкости из сечения 1 сместятся на расстояние 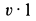
где 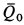
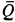
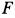
Так как в общей части объема жидкости количества движения, входящие в 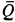
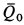
Сила давления жидкости 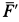
Проецируя (б) на оси координат, получаем
так как 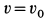
Направление силы давления жидкости 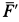
Рис. 43
Если бы через сечение 1 жидкость не поступала, а образовывалась внутри трубы, как в реактивном двигателе образуются газы после сгорания топлива, а через сечение 2 она выходила (рис. 43), то сила 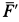
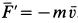
Эта сила 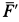
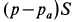
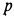
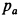
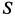
Полная реактивная сила двигателя
По направлению реактивная сила 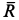
- Заказать решение задач по теоретической механике
Теорема о движении центра масс системы
Следствием теоремы об изменении количества движения системы является теорема о движении центра масс системы. По теореме об изменении количества движения системы (13),
Но количество движения системы можно вычислить по формуле (6):
где 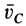
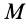
Подставляя (6) в (13) и учитывая, что масса системы постоянна, получаем теорему о движении центра масс в векторной форме:
или
где 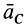
Рис. 44
Теорема о движении центра масс формулируется так: центр масс системы движется так же, как и материальная точка, масса которой равна массе всей системы, если на точку действуют все внешние силы, приложенные к рассматриваемой механической системе.
Проецируя (18) на прямоугольные декартовы оси координат (рис. 44), получаем дифференциальные уравнения движения центра масс:
где 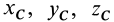
Из теоремы о движении центра масс можно получить следствия, аналогичные законам сохранения количества движения и проекции количества движения на ось.
1. Если главный вектор внешних сил, действующих на систему, равен нулю, т. е. 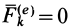
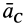
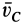
2. Если проекция, например на ось 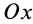
то из (18′) следует, что проекция ускорения 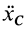
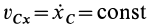
Рис. 45
Если дополнительно в начальный момент 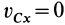
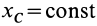
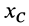
Внутренние силы не влияют явно на движение центра масс. Они могут влиять только неявно, через внешние силы. Следовательно, одними внутренними силами, без внешних, нельзя вывести из равновесия или изменить движение центра масс системы. Но внутренними силами для неизолированной механической системы можно создать движение отдельных частей системы и, следовательно, взаимодействие с внешними телами, вызывая этим внешние силы реакций связей или изменяя активные силы. Это может изменить движение центра масс или вывести его из равновесия.
Пусть человек стоит на абсолютно гладкой горизонтальной плоскости вблизи скрепленного с этой плоскостью тела. Так как на человека не действуют внешние силы в горизонтальном направлении, то внутренними силами он не может вывести из равновесия в этом направлении свой центр масс. Но человек может оттолкнуться рукой от препятствия, т. е. внутренними силами вызвать внешнюю силу реакций препятствия и таким образом вызвать движение своего центра масс в горизонтальном направлении. Все, что движется по Земле, летает в воздухе, плавает по воде, совершает это с помощью внутренних сил, создавая внешние силы трения на твердых поверхностях внешних тел, отталкиваясь от воздуха или воды.
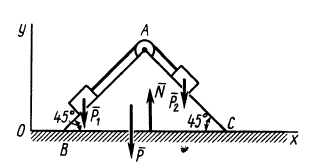
Пример №2
Два груза с силами тяжести 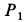
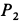
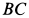
Найти перемещение клина по плоскости при опускании груза 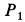
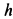
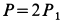
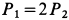
Решение:
Внешними силами, действующими на клин вместе с грузами, являются силы тяжести 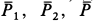
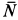
Учитывая, что в начальный момент система находится в покое, на основании второго следствия из теоремы о движении центра масс имеем 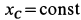
Вычислим 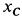
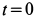
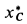
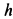
Для момента
где 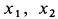
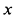
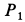
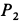
Пусть вся система вместе с клином переместилась в положительном направлении оси 
так как грузы вместе с клином передвинутся на 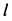
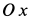
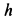
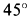
Так как 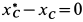
Отсюда
Так как величина 
Рис. 46
Пример №3
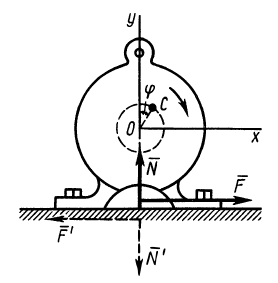
В электромоторе корпус (статор) имеет силу тяжести 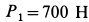
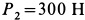
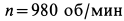
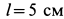
Определить горизонтальную силу, с которой действует мотор на болты, крепящие его к фундаменту, и вертикальное давление на пол.
Решение:
Предположим, что при 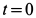
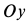
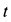
где
Для определения давления мотора на болты и пол рассмотрим в качестве механической системы весь мотор, для которого внешней силой в горизонтальном направлении является только сила действия болтов 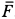
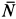
где 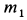
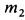
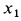
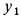
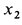
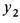
Центр масс корпуса закрепленного мотора является неподвижной точкой и находится в начале координат. Следовательно, 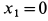
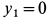
Используя дифференциальные уравнения движения центра масс всего мотора в проекциях на координатные оси, получим
где 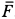
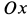
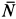
то из (а) следует
Сила действия мотора на болты 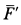
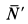
Наибольшие числовые значения этих сил
Если болтов нет, то корпус мотора может подпрыгивать в направлении оси 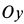
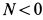
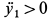
Дифференциальные уравнения поступательного движения твердого тела
Из теоремы о движении центра масс системы получаются дифференциальные уравнения поступательного движения твердого тела. Имеем
Но при поступательном движении твердого тела ускорения всех точек тела одинаковы по модулю и направлению, т. е. 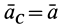
Проецируя на оси координат, имеем:
Это и есть дифференциальные уравнения поступательного движения твердого тела в проекциях на прямоугольные оси координат. В этих уравнениях х, у, z являются координатами произвольной точки тела, в частности могут быть координатами его центра масс. Тело, совершающее поступательное движение, имеет три степени свободы, и поэтому можно составить три дифференциальных уравнения его движения.
Дифференциальные уравнения поступательного движения твердого тела аналогичны дифференциальным уравнениям движения одной материальной точки. С помощью этих уравнений можно решать такие же задачи, как и для одной точки.
- Теорема об изменении кинетического момента
- Теорема об изменении кинетической энергии
- Потенциальное силовое поле
- Закон сохранения механической энергии
- Относительное движение материальной точки
- Геометрия масс
- Свойства внутренних сил системы
- Дифференциальное уравнение движения системы
Количество движения материальной точки – векторная величина, равная произведению массы точки на вектор ее скорости.
Единицей измерения количества движения является (кг м/с).
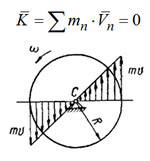
Количество движения механической системы – векторная величина, равная геометрической сумме (главному вектору) количества движения механической системы равняется произведению массы всей системы на скорость ее центра масс.
Когда тело (или система) движется так, что ее центр масс неподвижен, то количество движения тела равняется нулю (например, вращение тела вокруг неподвижной оси, проходящей через центр масс тела).
В случае сложного движения, количество движения системы не будет характеризовать вращательную часть движения при вращении вокруг центра масс. Т.е., количество движения характеризует только поступательное движение системы (вместе с центром масс).
Импульс силы
Импульс силы характеризует действие силы за некоторый промежуток времени.
Импульс силы за конечный промежуток времени определяется как интегральная сумма соответствующих элементарных импульсов.
Теорема об изменении количества движения материальной точки
(в дифференциальной форме):
Производная по времени от количества движения материальной точки равна геометрической сумме действующих на точки сил.
(в интегральной форме):
Изменение количества движения материальной точки за некоторый промежуток времени равняется геометрической сумме импульсов сил, приложенных к точке за этот промежуток времени.
Теорема об изменении количества движения механической системы
(в дифференциальной форме):
Производная по времени от количества движения системы равна геометрической сумме всех внешних сил, действующих на систему.
(в интегральной форме):
Изменение количества движения системы за некоторый промежуток времени равняется геометрической сумме импульсов внешних сил, действующих на систему за этот промежуток времени.
Теорема позволяет исключить из рассмотрения заведомо неизвестные внутренние силы.
Теорема об изменении количества движения механической системы и теорема о движении центра масс являются двумя разными формами одной теоремы.
Закон сохранения количества движения системы
- Если сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянным по направлению и по модулю.
- Если сумма проекций всех действующих внешних сил на любую произвольную ось равна нулю, то проекция количества движения на эту ось является величиной постоянной.
Выводы:
- Законы сохранения свидетельствуют, что внутренние силы не могут изменить суммарное количество движения системы.
- Теорема об изменении количества движения механической системы не характеризует вращательное движение механической системы, а только поступательное.
Приведен пример: Определить количество движения диска определенной массы, если известна его угловая скорость и размер.
Пример решения задачи на применение теоремы теоремы об изменении количества движения для определения скорости материальной точки
Теорема об изменении количества движения точки
Так как масса точки постоянна, а ее ускорение то уравнение, выражающее основной закон динамики, можно представить в виде
.
Уравнение выражает одновременно теорему об изменении количества движения точки в дифференциальной форме: производная по времениот количества движения точки равна геометрической сумме действующих на точку сил.
Проинтегрируем это уравнение. Пусть точка массы m, движущаяся под действием силы (рис.15), имеет в момент t=0 скорость
, а в момент t1-скорость
.
Рис.15
Умножим тогда обе части равенства на и возьмем от них определенные интегралы. При этом справа, где интегрирование идет по времени, пределами интегралов будут 0 и t1, а слева, где интегрируется скорость, пределами интеграла будут соответствующие значения скорости
и
. Так как интеграл от
равен
, то в результате получим:
.
Рекомендуемые материалы
Стоящие справа интегралы представляют собою импульсы действующих сил. Поэтому окончательно будем иметь:
.
Уравнение выражает теорему об изменении количества движения точки в конечном виде: изменение количества движения точки за некоторый промежуток времени равно геометрической сумме импульсов всех действующих на точку сил за тот же промежуток времени (рис. 15).
При решении задач вместо векторного уравнения часто пользуются уравнениями в проекциях.
В случае прямолинейного движения, происходящего вдоль оси Ох теорема выражается первым из этих уравнений.
Пример 9. Найти закон движения материальной точки массы m, движущейся вдоль оси х под действием постоянной по модулю силы F (рис. 16) при начальных условиях: ,
при
.
Рис.16
Решение. Составим дифференциальное уравнение движения точки в проекции на ось х: . Интегрируя это уравнение, находим:
. Постоянная
определяется из начального условия для скорости и равна
. Окончательно
.
Далее, учитывая, что v = dx/dt, приходим к дифференциальному уравнению: , интегрируя которое получаем
.
Постоянную определяем из начального условия для координаты точки. Она равна
. Следовательно, закон движения точки имеет вид
.
Пример 10. Груз веса Р (рис.17) начинает двигаться из состояния покоя вдоль гладкой горизонтальной плоскости под действием силы F = kt. Найти закон движения груза.
Рис.17
Решение. Выберем начало отсчета системы координат О в начальном положении груза и направим ось х в сторону движения (рис. 17). Тогда начальные условия имеют вид: x(t = 0) = 0,v(t = 0) = 0. На груз действуют силы F, P и сила реакции плоскости N. Проекции этих сил на ось х имеют значения Fx = F = kt, Рx = 0, Nx = 0, поэтому соответствующее уравнение движения можно записать так: . Разделяя переменные в этом дифференциальном уравнении и затем интегрируя, получим: v = gkt2/2P + C1. Подставляя начальные данные (v(0) = 0), находим, чтоC1 = 0, и получаем закон изменения скорости
.
Последнее выражение, в свою очередь, является дифференциальным уравнением, интегрируя которое найдем закон движения материальной точки: . Входящую сюда постоянную определяем из второго начального условия х(0) = 0. Легко убедиться, что
. Окончательно
.
Пример 11. На груз, находящийся в покое на горизонтальной гладкой плоскости (см. рис. 17) на расстоянии a от начала координат, начинает действовать в положительном направлении осиx сила F = k2(P/g)x,где Р – вес груза. Найти закон движения груза.
Решение. Уравнение движения рассматриваемого груза (материальной точки) в проекции на ось х
. (1)
Начальные условия уравнения (1) имеют вид: x(t = 0) = a, v(t = 0) = 0.
Входящую в уравнение (1) производную по времени от скорости представим так
.
Подставляя это выражение в уравнение (1) и сокращая на (P/g), получим
.
Разделяя переменные в последнем уравнении, находим, что . Интегрируя последнее, имеем:
. Используя начальные условия
, получаем
, и, следовательно,
,
. (2)
Поскольку сила действует на груз в положительном направлении оси х, то ясно, что в том же направлении он должен и двигаться. Поэтому в решении (2) следует выбрать знак «плюс». Заменяя дальше во втором выражении (2) на
, получаем дифференциальное уравнение для определения закона движения груза. Откуда, разделяя переменные, имеем
.
Интегрируя последнее, находим: . После нахождения постоянной
окончательно получаем
или
.
Пример 12. Шар M массы m (рис.18) падает без начальной скорости под действием силы тяжести. При падении шар испытывает сопротивление , где
–постоянный коэффициент сопротивления. Найти закон движения шара.
Рис.18
Решение. Введем систему координат с началом в точке местоположения шара при t = 0, направив ось у вертикально вниз (рис. 18). Дифференциальное уравнение движения шара в проекции на ось у имеет тогда вид
. (1)
Начальные условия для шара записываются так: y(t = 0) = 0, v(t = 0) = 0.
Разделяя переменные в уравнении (1)
и интегрируя, находим: , где
. Или после нахождения постоянной
или
. (2)
Отсюда следует, что предельная скорость, т.е. скорость при , равна
.
Чтобы найти закон движения, заменим в уравнении (2) v на dy/dt. Тогда, интегрируя полученное уравнение с учетом начального условия, окончательно находим
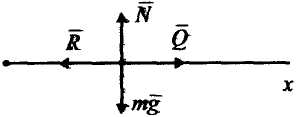
.
Пример 13. Научно-исследовательская подводная лодка шарообразной формы и массы m = = 1.5×105кг начинает погружаться с выключенными двигателями, имея горизонтальную скорость vх0 = 30 м/с и отрицательную плавучесть Р1 = 0.01mg, где – векторная сумма архимедовой выталкивающей силы Q и силы тяжести mg, действующих на лодку (рис. 20). Сила сопротивления воды
,
кг/с. Определить уравнения движения лодки и ее траекторию.
Рис.20
Решение. Начало координат выберем в начальном положении лодки, ось Ox направим горизонтально, а ось Oy – вертикально вниз (см. рис. 20). На лодку действуют три силы: P=mg – вес лодки, Q – архимедова выталкивающая сила, причем , и сила сопротивления R. Лодку примем за материальную точку M. Тогда второй закон Ньютона запишется так:
. В проекциях на оси Ox и Oy он будет иметь вид:
,
. Перепишем эти уравнения в форме системы уравнений первого порядка
,
.
Интегрируя их методом разделения переменных, получаем
,
.
После интегрирования и подстановки численных значений параметров и начальных данных находим
Закон движения находим из решения дифференциальных уравнений
,
.
Он описывается соотношениями
Если Вам понравилась эта лекция, то понравится и эта — Тема 15 — Организация и оказание первой медицинской помощи.
м.
В заключение найдем траекторию y (x). Для этого из первого уравнения выразим время t через координату х
.
Подставляя это выражение во второе уравнение, находим
.