✔ Читать статью полностью… ✔
✔ Открыть новый сайт ✔
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
И хотя сегодня теорема Пифагора обнаружена различных частных задачах и чертежах и египетском треугольнике папирусе времен фараона Аменемхета ок, и древнейшем китайском трактате Чжоуби суань цзинь Математический трактат гномоне, время создания которого точно не известно, но где утверждается, что. Первые доказательства нашли у какихто индийских математиков за несколько столетий до Пифагора. Алгебраическая формулировка В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Сферический аналог теоремы Пифагора Выведем аналог теоремы Пифагора на сфере выражение гипотенузы прямоугольного сферического треугольника через его катеты. Доказательство простейшее Это доказательство получается простейшем случае равнобедренного прямоугольного треугольника. При этом можно рассмотреть доказательства, в которых квадрат, построенный на гипотенузе данного прямоугольного треугольника.
В написанном на пальмовых листьях трактате Сиддханта широмани Венец знания крупнейшего индийского математика. Формы занятий предусматривают исследовательскую и проектную деятельность учеников. А ведь при этом исчезает бесследно та первозданная геометрическая сущность теоремы, что привела древних мудрецов к истине. На данный момент научной литературе зафиксировано 367 доказательств данной теоремы. Исследовать различные способы доказательства данной теоремы, не рассматриваемые. От двух равных площадей нужно отнять равновеликие части так, чтобы одном случае остались два квадрата, построенные на катетах, а другом квадрат, построенный на гипотенузе. В игре 100 к 1 на вопрос Какие теоремы доказывают школьники? Это были великие математические открытия. Сферическая тригонометрия занимается изучением соотношений между сторонами и углами сферических треугольников например, на поверхности Земли и на небесной сфере.
Пифагора была жена по имени Феано, сын Телавг и дочь Мня по другой версии сын Аримнест и дочь Аригнота. Увы, от этого доказательства также не сохранилось никаких следов. Теорема Пифагора древнейшем китайском трактате Чжоуби суань цзинь. Пифагорейская система занятий состояла из трёх разделов учения числах арифметике, учения фигурах геометрии, учения строении Вселенной астрономии. То, что малые треугольники также подобны друг другу, следует из того, что каждый из них подобен большому треугольнику. Ферекид направил взор Пифагора к природе и ней одной советовал видеть своего первого и главного учителя. В этом контексте интересно заметить, что доказательство теоремы Пифагора выполняется путем построений, то потери сторон в о второй мировой войне время как обращение к фактическим площадям, возможно, привело бы к совершенно иной форме доказательства.
Доказательства методом площадей, Доказательство через.
Именно если квадрате со стороной с два заштрихованных треугольника. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Введя обозначения править Доказательства методом площадей Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. В их руках вычислительные рецепты, основанные крестьянский вопрос в 18 веке на смутных представлениях, превратились точную науку. Важно уравнение было занесено книгу рекордов Гиннесса вследствие 370 правдивых доказательств. Такое многообразие обьясняется тем, что теорема имеет. Арифметика как практика вычислений не интересовала Пифагора, и он с гордостью заявил, что поставил арифметику выше интересов торговца. Индийские ученые того времени обнаружили приблизительное вычисление гипотенузы треугольника, наделенного прямыми углами.
И пока он живет на острове Лесбос, знакомится с философом Ферекидом и учится у него медицине, астрологии, предсказанию затмений, тайнам чисел. Они не силах свету помешать, А могут лишь, закрыв глаза, дрожать От страха, что вселил них Пифагор. В школе Пифагора геометрия впервые оформляется самостоятельную научную дисциплину. Однако одни полагают, что Пифагор первым дал её полноценное доказательство, а другие отказывают ему и этой заслуге. То есть, обозначив длину гипотенузы треугольника через, а длины катетов через и 2. Размер 921мм это опять же, гипотенуза, значит катеты, равны 651мм каждый. Однажды во время игры Прямой угол заметил интересное свойство если ему удается найти катеты, то отыскать Гипотенузу не составляет труда. Продемонстрировать другим учащимся существование новых способов доказательства теоремы Пифагора.
Выход из очевидного кризиса несоизмеримостей был найден значительной степени благодаря возможности манипулировать их произведениями и отношениями посредством отношений Евдокса. Пользователь Гость вы не сможете редактировать или удалить оставленный комментарий. Заметим, что частные случаи теоремы Пифагора например, построение квадрата, площадь которого вдвое больше площади данного квадрата встречаются древнеиндийском трактате Сульва сутра —. Теорема Пифагора — пожалуй, самая известная из математических теорем. Первая версия предпочтительнее, так как Павсаний приводит генеалогию Пифагора по мужской линии от Гиппаса из пелопоннесского Флиунта, бежавшего на Самос и ставшего прадедом Пифагора 2 Партенида, позднее переименованная мужем Пифаиду, происходила из знатного рода Анкея, основателя греческой колонии на Самосе. По возвращении на Самос Пифагор основал свою школу, но затем покинул остров.
Разные способы доказательства теоремы Пифагора примеры.
Предполагается проведение собеседований, анкетирования с целью мониторинга динамики интереса к изучению курса, интереса к будущей профессиональной сфере. Слабые ученики, заучившие теоремы наизусть, без понимания, и прозванные поэтому ослами, были не состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста. Это следствие определения площади треугольника как половины произведения основания на высоту. Квадрат гипотенузы равен сумме квадратов катетов. Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения данном случае катет. Приведем современном изложении одно из таких доказательств, возможно принадлежащих Пифагору. Известны доказательства теоремы Пифагора, предложенные Евклидом. Атанасян, доказательство Евклида рассматривается учебнике Геометрия Учебник для 69 классов средней школы, А.
Все занятия направлены на развитие интереса школьников к предмету, на расширение представлений об изучаемом материале, на решение новых и интересных задач практической направленности. Попытаемся доказать, что площадь квадрата равна площади прямоугольника Для этого воспользуемся вспомогательным наблюдением Площадь треугольника с той же высотой и основанием, что и данный прямоугольник, равна половине площади заданного прямоугольника. Возьмём верёвку длиною 12 и привяжем к ней по цветной полоске на расстоянии 3 и 4 от одного конца. Треугольники со сторонами, выраженными мессенские войны у целыми числами, называют пифагоровыми. История теоремы Пифагора уходит в глубокую древность.
В конце девятнадцатого века высказывались разнообразные предположения существовании обитателей Марса подобных человеку, это явилось следствием открытий итальянского астронома Скиапарелли открыл на Марсе каналы, которые долгое время считались искусственными. Курс характеризуется рациональным сочетанием очерк вторая мировая война логической строгости и геометрической наглядности. Ему приписывают два фундаментальных открытия теорию отношений и метод исчерпывания. Эти части следующие треугольники 1, 2, 3, 4 прямоугольник 5 прямоугольник 6 и квадрат 8 прямоугольник 7 и квадрат 9 Затем выбросим из прямоугольника части так, чтобы остались только квадраты, построенные на катетах. В возрасте примерно 60 лет Пифагор женится на Феано, одной из своих учениц.
Доказательства теоремы Пифагора с точки зрения психологии.
Так, оптимист Михаил Ломоносов 17111765 писал Пифагор за изобретение классификация 370 доказательств теоремы пифагора дана одного геометрического правила Зевсу принес на жертву сто волов. В первом случае эта площадь равна Приравнивая эти выражения, получаем теорему Пифагора. Узнав, какое несчастье произошло с принцессой, молодой принц берется расколдовать. Здесь вы можете увидеть доказательство теоремы Пифагора, которое основано на равновеликости фигур, из которых они состоят. Идея данного доказательства дополнительно проиллюстрирована с помощью анимации, расположенной выше. Для того чтобы доказать теорему пользуясь первым рисунком достаточно только выразить площадь трапеции двумя путями. Здесь же он глубоко изучил математику, науку чисел или всемирных принципов, из которой впоследствии сделал центр своей системы. Помогает найти или днину стороны, или размер угла треугольника, используя функцию косинус.
Но теперь Пифагор более всего известен благодаря теореме, которая сейчас носит его. Причина такой популярности теоремы Пифагора объясняется её простотой, красотой, значимостью. Презентация на тему И способы ее доказательства Сколько. Следовательно, если треугольник прямоугольный, то сумма налоговый отчетный период это квадратов его катетов действительно равна квадрату гипотенузы. В зданиях готического и романского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. Нахождение диагоналей трапеции через ее основания, стороны и углы при большем. Однако, на деле, теорема Пифагора хоть классификация 370 доказательств теоремы пифагора дана и проста, но далеко не очевидна. Многие из проповедуемых ифагором принципов достойны подражания и сейчас.
Слайд 23 Различные способы доказательства Доказательства, классификация 370 доказательств теоремы пифагора дана основанные на использовании понятия равновеликости фигур. Левый зеленый параллелограмм имеет такую же площадь, как левая часть синего параллелограмма, потому что они имеют такое же основание и высоту. Именно он нашел теорию иррациональных количеств и конструкцию космических тел. Благодаря такому количеству доказательств, теорема Пифагора попала Книгу рекордов Гиннеса, как теорема с наибольшим количеством доказательств. Так же как и доказательство того, что сумма внутренних углов любого треугольника равна двум прямым. Вокруг икосаэдра описана сфера Земли, а вокруг этой сферы додекаэдр.
Треугольник составлен из двух половинок одинаковы прямоугольных треугольников, гипотенузы русская государственность в период феодальной раздробленности которых и должны быть связаны с катетами по теореме Пифагора. Собственно, все доказательство состоит из чертежа, похожего на вышеприведенный китайский. Это очень важные вопросы, определившие весь дальнейший после Пифагора путь развития античной математики, имя которому — геометрическая алгебра. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности. Администрация сайта сможет удалить или редактировать Ваш комментарий. И, может быть, отсюда пошла та числовая мистика приписывания числам божественной силы, которая Пифагором была преподнесена как философия. Слайд 34 Алгебраический способ доказательства теоремы.
Теорема Пифагора история вопроса, доказательства, примеры.
В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников. А вот ироничный Генрих Гейне 1797 — 1856 видел развитие той же ситуации несколько иначе Кто знает! Укладывая эти треугольники так, как показывает рисунок, получим посредине квадрат. Методическое пособие для учителя с методическими рекомендациями по проведению классификация 370 доказательств теоремы пифагора дана занятий, решению задач, организации промежуточного и итогового контроля знаний учащихся. Для того, чтобы доказать теорему гиппократовых луночках, докажем следующее предложение Если на катетах и на гипотенузе прямоугольного треугольника построены какие угодно подобные между собой.
Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол теорема читается так, В переводе это означает Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу. Во всех этих случаях для понимания доказательства достаточно одного взгляда на чертеж рассуждение здесь может быть ограничено единственным словом Смотри! Поэтому нам ничего не остается, как рассмотреть некоторые классические доказательства теоремы Пифагора, известные из древних трактатов. Простейший пример применения этого метода имеем при доказательстве теоремы Пифагора для равнобедренного прямоугольного треугольника.
Сущность этого метода состоит том, что к квадратам, построенным на катетах, и к квадрату, построенному на гипотенузе, присоединяют равные фигуры таким образом, чтобы получились равновеликие фигуры. Способы ее доказательства Сложно, наверно, найти человека, у кого бы имя Пифагора ассоциировалось бы не с теоремой Пифагора. Но никто не мешает выстроить курс иначе, тем более что к этому есть все предпосылки теорему Фалеса доказывают обычно очень рано, а. Какой путь проходит луч? При пожаре пифагорейцы спасли жизнь своему учителю ценой своей, после чего Пифагор затосковал и вскоре покончил жизнь самоубийством. Разумеется, концептуально все их можно разбить на малое число классов. Отмерив на столешнице 425мм, мы знаем, что размер под стык столешниц. Свою школу Пифагор создает как тайную организацию со строго ограниченным числом учеников из аристократии, и попасть нее было не просто.
Теорема Пифагора формула, доказательство и примеры решений.
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы, она занесена в книгу рекордов Гиннеса. Квадрат составного числа равен разности квадратов одной пары или нескольких пар чисел. Есть две полярных точки зрения на этот вопрос. Равенство площадей устанавливается в нем с помощью некоторого преобразования. Будь с тем, кто ношу взваливает, не будь с тем, кто ношу сваливает. Игарёха Микишин 133, закрыт 5 лет назад Доказательство теоремы Пифагора.
На самом деле существует много способов доказательства теоремы Пифагора доказательство Евклида, Хоукинса. Как мы уже видели, древности эта теорема была известна практически повсеместно. На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы 9. Р анее были представлены только такие доказательства, которых квадрат, построенный на гипотенузе, с одной стороны, и квадраты, построенные на катетах, с другой, складывались из равных частей. Эта цепочка рассуждений, которая с помощью законов логики сводит неочевидные утверждения к известным или очевидным истинам, и есть математическое доказательство. Самостоятельно докажите попарное равенство треугольников, полученных при разбиении квадратов, построенных на катетах и гипотенузе. Из за чертежей, сопровождающих теорему Пифагора, учащиеся называли ее так же ветряной мельницей, составляли стихи вроде Пифагоровы штаны на все стороны равны, рисовали карикатуры.
Дело том, что некоторых списках Начал Евклида эта теорема называлась теоремой нимфы за сходство чертежа с пчелкой, бабочкой, что погречески называлось нимфой. Такое многообразие можно объяснить лишь фундаментальным значением. Десятая книга содержит подробный анализ различных иррациональных длин, и именно здесь мы находим идею несоизмеримости между основными величинами, сводящуюся к понятию иррациональности между длинами и площадями. На данный момент наукой зафиксировано более 400 способов доказательства теоремы Пифагора. Теорема Пифагора послужила источником для множества обобщений и плодородных идей. Пифагор замечательный оратор, учитель и воспитатель, организатор своей школы, ориентированной на гармонию музыки и чисел, добра и справедливости, на знания и здоровый образ жизни. Его историю можно разделить на два обширных периода переход от одного к другому ознаменовался началом царствования Александра Великого.
Доказать Квадрат гипотенузы равен сумме квадратов катетов Теорема Пифагора. Это прямоугольный треугольник На этом свойстве прямоугольного треугольника и основана теорема Пифагора. Если мы от первого из них отнимем треугольники 1 и 2, то останутся квадраты, построенные на катетах, а если от второго шестиугольника отнимем равные треугольники 1 и 3, то останется квадрат, построенный на гипотенузе. Доказательства, основанные на использовании понятия равновеликости фигур. Ведь целых сто быков послал он под топор, Чтоб их сожгли как жертвоприношенье. Если Пифагор действительно предложил такое доказательство, то он был знаком и с целым рядом важных геометрических теорем, которые современные историки математики обычно приписывают Евклиду. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать. Викия — это свободный ресурс, который существует и развивается за счёт рекламы. Когда однажды Пифагора спросили, что такое друг, он сказал, что это второе я, как числа 220 и.
Вам предстоит поискать эти доказательства и выучить хотя бы одно из. В школе существовал декрет, по которому авторство всех математических работ приписывалось учителю Слайд 4 В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Молниеотвод защищает от молнии все предметы, расстояние которых от его основания не превышает его удвоенной высоты. Лишь, глаза закрыв, реветь, дрожать. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна 4, один катет равен 4, а другой. Наверное, среди самых удивительных и противоречивых домыслов есть самородки истины, но огромная тяжесть ушедшего времени вдавила, растворила их этом фантастическом окружении, сделала невидимым и для.
- Текст
- Веб-страница
The Pythagorean» theorem is one of the most important propositions in the entire realm of geometry. Despite the strong Greek tradition that associates the name of Pythagoras with the statement that «the square on the hypotenuse of the right-angled triangle is equal
to the square on the sides containing the right angle», there is no doubt that this result was known prior to the time of Pythagoras.
It is possible that Pythagoras gave the proof of the theorem based on the proportionality of similar figures. With the later realization that all lines are not necessarily commensurable, this proof became invalid. Thus, at the time of Euclid’s Element’s there was no need for a more adequate proof. Euclid’s Proposition 147 is the Pythagorean theorem, with a proof universally credited to Euclid himself. Proclus’ speculation was simply that Euclid rewrote the proof in order that he might pul the proposition in his first book to complete it. There is also considerable evidence that the first book was written to lead to the climax of this theorem and its converse.
In 1907 L.S. Loomis published his book The Pythagorean Proposition, a work that contained 370 proofs of this theorem. Probably no other theorem in maths can be demonstrated by such a wide variety of algebraic and geometric proofs. The Pythagorean theorem and the proof are so important in maths that Loomis writes in his book: «I noticed two or three American texts on geometry in which Euclid’s proof of the Pythagorean theorem does not appear. I suppose the author wishes to show his originality or independence — possibly up-to-dateness. He shows something else. The leaving out of Euclid’s proof is like the play of Hamlet with Hamlet left out.
0/5000
Результаты (русский) 1: [копия]
Скопировано!
Теорема Пифагора» является одним из наиболее важных предложений в отношении всей геометрии. Несмотря на сильные греческой традиции, которая связывает имя Пифагора с заявлением, что «квадрат на гипотенузу angled треугольника равна до площади по бокам, содержащие правильный угол», нет никаких сомнений в том, что этот результат был известен до времени Пифагора. Вполне возможно, Пифагор дал доказательство теоремы, на основе пропорциональности аналогичных фигур. С более поздней реализации, что все линии не обязательно соизмеримо, это доказательство стало недействительным. Таким образом в то время Евклида элемента нет необходимости для более адекватного доказательства. Евклида предложение 147 является теорема Пифагора с универсально зачисленных Евклида, сам доказательство. Прокл спекуляции было просто, что Евклид переписал доказательство, с тем чтобы он мог бы Пульи предложение в своей первой книге, чтобы завершить его. Существует также значительные доказательства того, что первая книга была написана, чтобы привести к кульминации этой теоремы и ее обратное. В 1907 году л. с. Loomis опубликовал свою книгу Пифагора предложение, работа, которая содержит 370 доказательства этой теоремы. Вероятно другие теоремы, в математике может продемонстрировать широкий спектр алгебраические и геометрических доказательств. Теорема Пифагора и доказательство настолько важны в математике, что Лумис пишет в своей книге: «я заметил два или три американских текстов по геометрии, в которой Евклида доказательство теоремы Пифагора не появляется. Наверное, автор хочет показать свою оригинальность или независимость — возможно современность. Он показывает что-то другое. Выезд из доказательство Евклида, как играть Гамлета с Гамлет ушел.
переводится, пожалуйста, подождите..
Результаты (русский) 3:[копия]
Скопировано!
теорема пифагора «является одной из наиболее важных предложений во всей сфере геометрии.несмотря на сильную греческая традиция, что связывает имя пифагора с заявлением о том, что «площади по гипотенуза из прямоугольного треугольника равнына площадь, по бокам, содержащий под прямым углом «, нет никаких сомнений в том, что этот результат был известен до времени пифагора.вполне возможно, что пифагор дали доказательство теорема на основе соразмерности аналогичные цифры.после осознания того, что все линии не обязательно тем, доказательства были признаны недействительными.таким образом, на момент эвклид — элемента, нет необходимости в более надлежащее доказательство.евклид предложение 147 — теоремы пифагора, в доказательство повсеместно на евклид себя.прокл «спекуляция просто, что евклид переписал доказательства, с тем чтобы он мог — пул предложение в его первую книгу, чтобы завершить его.также существует достаточно доказательств того, что первая книга была написана, приведет к кульминации этой теоремы и наоборот.в 1907 г. лумис опубликовал книгу пифагора предложение, работа, которая содержит 370 доказательства этой теоремы.вероятно, никакой другой — по математике можно продемонстрировать посредством таких разнообразных алгебраических и геометрической доказательства.теоремы пифагора и доказательства так важны в математике, что лумис, пишет в своей книге: «я заметил двух или трех американских текстов по геометрии, в котором эвклид — доказательство теоремы пифагора не появляется.я полагаю, автор хочет показать его оригинальность или независимости — возможно, актуальность.он показывает, что — то еще.выход из евклид, доказательства — это как играть гамлета с гамлетом, уехали.
переводится, пожалуйста, подождите..
Другие языки
- English
- Français
- Deutsch
- 中文(简体)
- 中文(繁体)
- 日本語
- 한국어
- Español
- Português
- Русский
- Italiano
- Nederlands
- Ελληνικά
- العربية
- Polski
- Català
- ภาษาไทย
- Svenska
- Dansk
- Suomi
- Indonesia
- Tiếng Việt
- Melayu
- Norsk
- Čeština
- فارسی
Поддержка инструмент перевода: Клингонский (pIqaD), Определить язык, азербайджанский, албанский, амхарский, английский, арабский, армянский, африкаанс, баскский, белорусский, бенгальский, бирманский, болгарский, боснийский, валлийский, венгерский, вьетнамский, гавайский, галисийский, греческий, грузинский, гуджарати, датский, зулу, иврит, игбо, идиш, индонезийский, ирландский, исландский, испанский, итальянский, йоруба, казахский, каннада, каталанский, киргизский, китайский, китайский традиционный, корейский, корсиканский, креольский (Гаити), курманджи, кхмерский, кхоса, лаосский, латинский, латышский, литовский, люксембургский, македонский, малагасийский, малайский, малаялам, мальтийский, маори, маратхи, монгольский, немецкий, непальский, нидерландский, норвежский, ория, панджаби, персидский, польский, португальский, пушту, руанда, румынский, русский, самоанский, себуанский, сербский, сесото, сингальский, синдхи, словацкий, словенский, сомалийский, суахили, суданский, таджикский, тайский, тамильский, татарский, телугу, турецкий, туркменский, узбекский, уйгурский, украинский, урду, филиппинский, финский, французский, фризский, хауса, хинди, хмонг, хорватский, чева, чешский, шведский, шона, шотландский (гэльский), эсперанто, эстонский, яванский, японский, Язык перевода.
- I am at school! My teacher is sad! Why?H
- person can be punished for his politenes
- 15.11.2016 года в группе 03304 прошло ме
- куда идет этот студент
- 15.11.2016 года в группе 03304 прошло ме
- Once there lived two brothers — Jim and
- Read and write: true or false
- Where’should chuckles
- I sleep wake up at seven in the morning
- Qorxma
- Я сижу на стуле
- Не бойся
- Сколько комнат было в вашей старой кварт
- Вдруг всё смолкло
- Теперь
- Моя семья любит спортМы Костерины. Мы лю
- 1. Кто сегодня дежурный? – Елена. Сегодн
- Я сижу на стуле
- Belgārum a provincia longe abest, ubi cu
- 1. Кто сегодня дежурный? – Елена. Сегодн
- Which allows people to talk to each othe
- What does he look like
- мне нравится кукольный театр
- I am at school! My teacher is sad! Why?H
УДК 514-01
ТЕОРЕМА ПИФАГОРА. ЧЕТЫРЕ НОВЫХ ДОКАЗАТЕЛЬСТВА THE PYTHAGOREAN THEOREM. FOUR NEW EVIDENCE
В.М. Московкин V.M. Moskovkin
Белгородский национальный исследовательский университет, Россия, 308015, г. Белгород, ул. Победы, 85
Belgorod National Research University, 85 Pobedy St, Belgorod, 308015, Russia
E-mail: moskovkin@bsu.edu.ru
Аннотация. Проделаны четыре новых доказательства теоремы Пифагора, первые два из которых получены из подобия треугольников, а последнее два — из подобия треугольников и подсчета площадей треугольников. В отличие от известных доказательств теоремы Пифагора два последних доказательства свелись к случаю, когда произведение двух алгебраических членов равнялось нулю. Приравнивание к нулю первого члена сводилось к доказательству общего случая теоремы Пифагора, а второго — к частному случаю, который легко доказывается. Теорема Пифагора хороший пример для математического образования школьников и студентов, так как количество доказательств здесь не органично. Доказательства этой теоремы различными способами являются очень хорошими алгебро-геометрическими упражнениями. В школах и университетах могут объявляться конкурсы на наибольшее количество доказательств теоремы Пифагора. В этих конкурсах, возможно, будут найдены новые доказательства этой теоремы. Все это может вылиться в некое движение под названием «Пифагореана», что будет очень полезным в деле повышения престижа математического образования среди молодежи.
Resume. The article presents four new proof of Pythagoras’ theorem, the first two of which are derived from the similarity of triangles, and the last two from the similarity of triangles and calculation of the area of triangles. In contrast to the known proof of Pythagoras’ theorem, two recent proofs were reduced to the case when the product of two algebraic numbers is equal to zero. Equating to zero the first member reduced to the proof of the General case of Pythagoras’ theorem, and the second to the particular case which can easily be proved. Pythagoras’ theorem is a good example for the mathematics education of pupils and students as well as the number of proofs are not naturally. The proofs of this theorem by various methods are very good algebraic-geometric exercises. In schools and universities these theorems may be advertised competitions for the highest number proofs of Pythagoras’ theorem. In these competitions, possibly, new proof of this theorem can be found. All this can result in a movement called «Pythagorean» that will be very useful in increasing the prestige of mathematics education among young people.
Ключевые слова: Теорема Пифагора, новые доказательства теоремы Пифагора, подобие треугольников.
Key words: Pythagoras’ theorem, new proofs of Pythagoras’ theorem, similarity of triangles.
Одним из самых выдающихся достижений античной математики является теорема Пифагора. Она лежит в основе большей части евклидовой геометрии и всей тригонометрии [1,2], ньютоновой физики и релятивистской динамики [3,4]. Например, работе [3] доказано, что теорема Пифагора лежит в основе трех законов Ньютона, универсальной гравитационной силы, закона Кулона и формул релятивисткой динамики. Уже несколько тысячелетий к этой теореме приковано пристальное внимание профессионалов и любителей.
Наш поиск различных названий теоремы Пифагора с помощью поисковой машины Google Scholar (расширенный поиск с точной фразой) привел к следующим результатам (табл. 1).
Таблица 1 Table 1
Встречаемость различных названий теоремы Пифагора. Google Scholar. 22.01.2016 г. The incidence of different names of the Pythagorean theorem. Google Scholar. 22.01.2016 Mr.
Название Встречаемость названий в тексте научной публикации Встречаемость названий в заголовке научной публикации
Pythagorean Theorem 24800 353
Pythagoras Theorem 11200 110
Theorem of Pythagoras 2730
Теорема Пифагора 1480 41
Пифагорова теорема 11 15 0
Всего 40221 519
Из таблицы 1 видим, что наблюдается около 40 тысяч научных публикаций (в основном научные статьи) в которых встречается термин «Теорема Пифагора» на русском и английском языке.
Часто Теорема Пифагора используется в обучающих целях, например, в работе [5] для этих целей рассмотрено пять традиционных доказательств теоремы Пифагора.
Новые и старые доказательства теоремы Пифагора можно увидеть в работах конца 19 -начала 20 века [6,7]. Шесть новых доказательств этой теоремы предложено в работе [8]. Три новых доказательства теоремы Пифагора были сделаны в рамках студенческого проекта в университете Северной Флориды [9].
В связи с постоянным увеличением числа доказательств теоремы Пифагора в работе [10] был поставлен вопрос о неограниченном числе доказательств этой теоремы.
Наиболее полная подборка доказательств теоремы Пифагора собрана в книге [1], изданной Национальным советом учителей математики (США). В ней отмечается, что на уровень первого издания этой книги было собрано 230 различных доказательств теоремы Пифагора (1927 г.), а на уровень второго издания — 370 (1940 г.). В последнем случае из 370 доказательств выделено 109 алгебраических и 225 геометрических. С 6 мая 1997 г. по настоящее время на сайте Cut the Knot. Interactive Mathematics Miscellany and Puzzles (www.cut-cut-the-knot.org/pythagoras/index-html) ведется сбор всех, имеющихся доказательств теоремы Пифагора. На конец декабря 2015 г. на нем было собрано 114 доказательств этой теоремы.
В этой связи, очевидно, что все доказательства теоремы Пифагора, которые претендуют на новизну, должны быть протестированы на вышеуказанном сайте, а также по книге [1].
Из всех имеющихся доказательств теоремы Пифагора наибольший интерес представляют те, которые требуют минимум геометрических построений и алгебраических выкладок. Таким требованиям, в первую очередь, удовлетворяет доказательство А.М. Лежандра, полученное в 1858 г. [1,2]. Приведем это изящное доказательство в обозначениях работы [2], за исключением обозначения длины высоты (h ).
Если в прямоугольном треугольнике провести на гипотенузу высоту, которая разделит ее на отрезки х и у , тогда из подобия двух новых образовавшихся прямоугольных треугольников получим соотношения (рис. 1)
х а а2
— = х = —; ас с
у Ь Ь2
Ь с с
a h b
x y
С
Рис. 1. Рисунок к доказательству Лежандра и к первому новому доказательству теоремы Пифагора
2 д2
a b 2 i 2 2 Учитывая, что X + y = С, получим—1—= c ^ a + b = c . Что и требовалось доказать.
c c
Другое оригинальное доказательство теоремы Пифагора, но несколько более сложное получил в 1876 г. 20-ый президент США Д.А. Гарфильд [1,2].
Достраивая два равновеликих прямоугольных треугольника до трапеции, как показано на рисунке 2, и вычисляя площадь трапеции двумя способами получим:
1(а + Ь)(а + Ь) = 1 аЬ +1 аЬ +1 с2 ^ (а + Ь)(а + Ь) = 2аЬ + с2 ^ а2 + Ь2 = с2.
Что и требовалось доказать.
b
a
a b
Рис. 2. Рисунок к доказательству Гарфильда
В этом доказательстве, в отличие от доказательства Лежандра, в котором требуется знание теоремы о подобии треугольников, используются только формулы для расчета площадей треугольника и трапеции.
Интерес к теореме Пифагора ничуть не уменьшился и в наше время. Из самых последних публикаций отметим работы [11-13], причем в последней работе, опубликованной в American Mathematical Monthly в мае 2015 г. было предложено очередное новое доказательство теоремы Пифагора.
Ниже мы опишем четыре новых доказательства теоремы Пифагора.
Четыре новых доказательства теоремы Пифагора
Доказательство 1. Рассматривая два подобных треугольника на рисунке 1, можно проделать следующие выкладки:
к а ке х к ак х к к
— = а = —; — = х = —; — =-=-
а е Ь а Ь Ь к е — х ак
c —
b
x
— = ——— ^ x(cb — ah) = bk2 ^ — (cb — ah) = bk2 к cb — ah b
a2h2 , ,2 f hc i ahc—= bh ^
b
a h h c a h
hc a h
— I hc — — = bh2 ^ b ) b
b
b
= bh2 ^
к (е — а — Ь ) = 0 ^ е = а + Ь . Теорема Пифагора доказана. Доказательство 2. Располагая симметрично катета с длиной а исходный прямоугольный треугольник и проводя высоту на гипотенузу симметричного треугольника, запишем базовые балансовые соотношения (рис.3)
к + к2 = к, (1) х + у = е. (2)
b
b
Рис. 3. Рисунок к второму новому доказательству теоремы Пифагора
Из подобия треугольников следуют следующие соотношения
h a , 2ab
— = — ^ h =-,
2b c c
ha hb
— = — ^ x = —. x b a
Поставляя (4) в формулу (3), получим
x =
2b2
(3)
(4)
(5)
Снова используя свойство подобия треугольников, получим
b _ h _ h2
a y c — x
Поставляя (6) в формулу (5), получим
c
а у
К
с —
2Ъ2
с2 — 2Ъ2
■h2 =
(с2 — 2Ъ2)Ъ
ас
(7)
Используя в последний раз свойство подобия треугольников, получим
К _с
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Ъ а а
Поставляя (7,8) в (i), с учетом (3), получим
сЬ + (с2 — 2Ъ2)Ъ _ 2аЪ
(8)
(9)
а
ас
Преобразуем равенство (9)
с2Ъ + (с2 — 2Ъ2 )Ъ = 2а2Ъ ^ 2е2Ъ — 2Ъ — 2а2Ъ = 0 ^ 2Ъ(с2 — а2 — Ь2) = 0 ^
с2 = а2 + Ъ2. Теорема Пифагора доказана. В терминологии работы [1] оба доказательства носят алгебраический характер. Доказательство 3. Построим на гипотенузе длиной с квадрат, направленный в сторону треугольника, тогда квадрат, построенный на катете длиной а, разобьётся на четыре треугольника с
площадями ^ , £2, £3 и £4 (рис. 4):
a
а-Ь Ь
Рис. 4. Рисунок к третьему и четвёртому новым доказательствам теоремы Пифагора
Среди этих треугольников мы видим прямоугольный треугольник с площадью кон-
груентный к исходному с длинами сторон а , Ъ и с (доказательство очевидное). Длины катета и гипотенузы прямоугольного треугольника с площадью £2 и длиной катета разной а — Ъ обозначим,
соответственно, х и у . Тогда остальные два прямоугольных треугольника с площадью £3 и £4 , слагающих квадрат со стороной а, будут иметь длины катетов, соответственно, а и а — х ; с и у . Из подобия прямоугольных треугольников следуют соотношения:
x Ъ _(а — Ъ)Ъ
‘ — — —J x —
а — Ъ а
а
а — Ъ а (а — Ъ)с
-^ —— y — ——
ус а
(ю) di)
с
с
Просуммируем площади всех четырех выше описанных прямоугольных треугольников, слагающих квадрат со стороной a . Тогда получим:
1 ab + — (a — b)x +1 a(a — x) +1 cy = a1. (12)
2 2 2 2
Поставляя в выражение (12) формулы (10, 11), получим
1 ab + 1(a — b) (a — bb)b + — (a1 — ab + b2) + — — b) = a2. (13)
2 2 a 2 2 a
Алгебраические выкладки с выражением (13) имеют вид
a2b + (a — b)2b + (a2 — ab + b2)a + (a — b)c2 = 2a3 ^
a2b + a2b — 2ab2 + b3 + a3 — a2b + ab2 + ac2 — bc2 = 2a3 => a2b — ab2 + b3 + a3 + ac2 — bc2 = 2a3 ^ b(a2 + b2 — c2) + a(c2 — a2 — b2 ) = 0 ^ (c2 — a2 — b2 )(a — b) = 0. (14)
Из тождества (14) следует, что либо a = b, либо c2 = a2 + b2, то есть для общего случая, когда a Ф b теорема Пифагора доказана.
Для частного случая она доказывается следующим образом. Построим на сторонах треугольника с равными катетами квадраты, как показано на рисунке 5.
a c
a
Рис. 5. Рисунок к третьему новому доказательству теоремы Пифагора для частного случая, когда a = b
Обозначим площадь исходного прямоугольника с равными катетами через S, тогда
c2 = 4S , 2a2 = 4S, то есть теорема Пифагора для частного случая a2 + a2 = c2 доказана.
Доказательство 4. Рассмотрим теперь квадрат, построенный на гипотенузе длиной c (рис.4).
bc
Из подобия треугольников с площадями S и S определим длину катета z : z = — . Представим
a
площадь квадрата, построенного на гипотенузе длиной c, в виде
c2 = S5 + S + a2 — S — S2 = a2 + S5 — S2. (15)
Поставляя в выражение (15) значения площадей S и S соответствующих прямоугольных
треугольников, вычисленные через половинные произведения их катетов, придем к следующим алгебраическим выкладкам
c2 = a2 + — — (a — b)2 b ^ 2c2a — c2b = 2a3 — a2b + 2ab2 — b3 ^ c2 (2a — b) = 2a 2a
= а1 (2а — Ъ) + Ъ1 (2а — Ъ) ^ (с2 — а2 — Ъ2 )(2а — Ъ) = 0.
(16)
Из тожества (16) следует, что либо 2а = Ъ, либо с2 = а2 + Ъ2, то есть для общего случая, когда 2а Ф Ъ, теорема Пифагора доказана.
Для доказательства частного случая построим рисунок 6.
С а С
а а а а
а а С
С
Рис. 6. Рисунок к четвертому новому доказательству теоремы Пифагора для частного случая, когда 2а = Ъ
Теорема Пифагора для рассматриваемого случая сводится к равенству а + Ъ = с ^ а2 + 4а2 = 5а2 = с2. Из рисунка 6 видим, что квадрат, построенный на гипотенузе с длиной с, слагается из одного квадрата с площадью а и четырех равновеликих прямоугольных треугольников,
каждый из которых имеет площадь а • 2а = а2. Следовательно, равенство 5а2 = с2 соблюдается.
Кстати, рисунок 6 очень хорошо известен из литературы, посвященной теореме Пифагора [1,2]. При стремлении Ъ к а внутренний квадрат на рисунке 6 стягивается к точке и этот рисунок вырождается в рисунок 5. Оба последних доказательства теоремы Пифагора носят алгебраический характер.
Как видим все четыре доказательства, как и большинство других доказательств теоремы Пифагора используют теорему о подобии треугольников. В отличие от известных доказательств наши новые доказательства теоремы Пифагора в двух последних случаях сводятся к случаю, когда произведение двух алгебраических членов равняется нулю. Приравнивание к нулю первого члена сводится к доказательству общего случая теоремы Пифагора, а второго — к частому случаю, который легко доказывается.
Заключение
Рассматривая различные доказательства теоремы Пифагора можно сделать вывод, что основная идея многих доказательств состоит в том, чтобы построить геометрическую фигуру на базе исходного прямоугольного треугольника и посчитать ее площадь двумя различными способами, а
потом прийти к тождеству с2 = а2 + Ъ2. Не достающие длины отрезков на этой фигуре обычно определяются из подобия треугольников.
Теорема Пифагора хороший пример для математического образования школьников и студентов, так как количество доказательств здесь не органично. Доказательства этой теоремы различными способами являются очень хорошими алгебро-геометрическими упражнениями. В школах и
университетах могут объявляться конкурсы на наибольшее количество доказательств теоремы Пифагора. В этих конкурсах, возможно, будут найдены новые доказательства этой теоремы. Все это может вылиться в некое движение под названием «Пифагореана», что будет очень полезным в деле повышения престижа математического образования среди молодежи.
Список литературы
1. Loomis E.S. 1986. The Pythagorean proposition. Washington: The Nacional Council of Teachers of Mathematics : 310.
2. Sparks J.C. 2008. The Pythagorean Theorem. Crown Jewel of Mathematics. Bloomington: Author House:
186.
3. Cui H.Y. To String together Six Theorems of Physics by Pythagoras Theorem // arXiv: physics / 0205021/V1/ [physics.gen -ph]
4. Orun L.B. The Theory of Relativity and the Pythagorean Theorem // arXiv: 0809.2379 V1 [physics.class —
ph]
5. Chambers P. 1999. Teaching Pythagoras Theorem. Mathematics in School, № 4 (28): 22-24.
6. Yanney B.F., Calderhead J.A. 1896. New and Old Proofs of the Pythagorean Theorem. The American Mathematical Monthey, № 4 (3): 110-113
7. Macfarlane A. 1911. The Pythagorean Theorem. Science. New Series, № 887(34): 181-182.
8. Kenney J.M. 1941. New Proofs of the Theorem of Pythagoras. School Science and Mathematics. № 3 (41):
249-254.
9. Spradlin M., Watkins M. 1998. Three New Proofs of the Pythagorean Theorem. Applied Probability Trust:
53-54.
10. Hoehn L. 1997. The Pythagorean Theorem: An Infinite Number of Proofs? The Mathematical Teacher, № 6 (90): 438-441.
11. Swaminathan S. 2014. The Pythagorean Theorem. Biodiversity. Bioprospecting and Development, № 3
(1): 4 .
12. Caglayan G. 2015. Pythagorean Theorem with Hippocrates’ Lunes. Spreadsheets in Education, № 2 (8) (article 5): p.
13. Heo N. G. 2015. A New Proof of the Pythagorean Theorem. The American Mathematical Monthly, № 5 (122): 451.
Эта статья о классической геометрии. Чтобы узнать о бейсболе, см. Пифагорейское ожидание.
теорема Пифагора
Сумма площадей двух квадратов на ножках (а и б) равна площади квадрата на гипотенузе (c).
| Геометрия | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|

Проектирование а сфера к самолет |
||||||||||
|
||||||||||
|
ветви
|
||||||||||
Размер
|
||||||||||
|
Нульмерный
|
||||||||||
|
Одномерный
|
||||||||||
|
Двумерный
|
||||||||||
|
Трехмерный
|
||||||||||
|
Четыре — / другое измерение
|
||||||||||
| Геометры | ||||||||||
|
по имени
|
||||||||||
|
по периоду
|
||||||||||
В математика, то теорема Пифагора, также известен как Теорема Пифагора, является фундаментальным соотношением в Евклидова геометрия среди трех сторон прямоугольный треугольник. В нем указано, что площадь квадрата со стороной гипотенуза (сторона, противоположная прямой угол ) равна сумме площадей квадратов на две другие стороны. Эта теорема можно записать как уравнение относя длины сторон а, б и c, часто называемое «уравнением Пифагора»:[1]
где c представляет длину гипотенузы, а а и б длины двух других сторон треугольника. Теорема, история которой является предметом многочисленных споров, названа в честь древнегреческий мыслитель Пифагор.
Теореме было дано множество доказательств — возможно, больше всего для любой математической теоремы. Они очень разнообразны, включая как геометрические, так и алгебраические доказательства, некоторые из которых датируются тысячелетиями. Теорема может быть обобщена различными способами, включая многомерные пространства, на пространства, не являющиеся евклидовыми, на объекты, которые не являются прямоугольными треугольниками, и действительно, на объекты, которые вообще не являются треугольниками, но п-мерные тела. Теорема Пифагора вызвала интерес за пределами математики как символ математической непонятности, загадочности или интеллектуальной силы; популярные ссылки в литературе, пьесах, мюзиклах, песнях, марках и мультфильмах имеются в большом количестве.
Доказательство перестановки
Доказательство перестановки (щелкните, чтобы просмотреть анимацию)
Каждый из двух больших квадратов, показанных на рисунке, содержит четыре идентичных треугольника, и единственная разница между двумя большими квадратами состоит в том, что треугольники расположены по-разному. Следовательно, белое пространство внутри каждого из двух больших квадратов должно иметь одинаковую площадь. Приравнивание площади белого пространства дает теорему Пифагора, Q.E.D.[2]
Хит приводит это доказательство в своем комментарии к предложению I.47 в книге Евклида. Элементы, и упоминает предложения Бретшнайдера и Ганкеля о том, что Пифагор мог знать это доказательство. Сам Хит поддерживает другое предложение о пифагорейском доказательстве, но с самого начала своей дискуссии признает, что «греческая литература, которой мы располагаем, относящаяся к первым пяти столетиям после Пифагора, не содержит утверждений, определяющих это или какое-либо другое конкретное великое геометрическое открытие для него. «[3] Недавние исследования поставили под сомнение какую-либо роль Пифагора как создателя математики, хотя споры по этому поводу продолжаются.[4]
Другие формы теоремы
Если c обозначает длина гипотенузы и а и б обозначают длины двух других сторон, теорема Пифагора может быть выражена как уравнение Пифагора:
Если длина обоих а и б известны, то c можно рассчитать как
Если длина гипотенузы c и с одной стороны (а или б) известны, то длину другой стороны можно рассчитать как
или
Уравнение Пифагора связывает стороны прямоугольного треугольника простым способом, так что, если известны длины любых двух сторон, можно найти длину третьей стороны. Другое следствие теоремы состоит в том, что в любом прямоугольном треугольнике гипотенуза больше любой другой стороны, но меньше их суммы.
Обобщением этой теоремы является закон косинусов, который позволяет вычислить длину любой стороны любого треугольника, учитывая длины двух других сторон и угол между ними. Если угол между другими сторонами является прямым, закон косинусов сводится к уравнению Пифагора.
Другие доказательства теоремы
У этой теоремы может быть больше доказательств, чем у любой другой (закон квадратичная взаимность будучи еще одним претендентом на это различие); книга Предложение Пифагора содержит 370 доказательств.[5]
Доказательство с использованием подобных треугольников
Доказательство с использованием подобных треугольников
Это доказательство основано на соразмерность из сторон двух аналогичный треугольников, то есть на том, что соотношение любых двух соответствующих сторон одинаковых треугольников одинакова независимо от размера треугольников.
Позволять ABC представляют собой прямоугольный треугольник с прямым углом, расположенным на C, как показано на рисунке. Нарисуйте высота с точки C, и позвонить ЧАС его пересечение со стороной AB. Точка ЧАС делит длину гипотенузы c на части d и е. Новый треугольник ACH является аналогичный в треугольник ABC, потому что они оба имеют прямой угол (по определению высоты), и у них общий угол при А, что означает, что третий угол будет одинаковым в обоих треугольниках, отмеченных как θ на рисунке. По аналогичным соображениям треугольник CBH также похож на ABC. Доказательство подобия треугольников требует постулат треугольника: Сумма углов в треугольнике равна двум прямым углам и эквивалентна параллельный постулат. Подобие треугольников приводит к равенству соотношений соответствующих сторон:
Первый результат равен косинусы углов θ, а второй результат приравнивает их синусы.
Эти отношения можно записать как
Суммируя эти два равенства, получаем
которая после упрощения выражает теорему Пифагора:
Роль этого доказательства в истории является предметом множества предположений. Основной вопрос заключается в том, почему Евклид не использовал это доказательство, а изобрел другое. Одно из предположений состоит в том, что доказательство с помощью подобных треугольников включало теорию пропорций, и эта тема обсуждалась позже в Элементы, и что теория пропорций в то время нуждалась в дальнейшем развитии.[6][7]
Доказательство Евклида
Доказательство у Евклида Элементы
В общих чертах, вот как доказательство в Евклид с Элементы продолжается. Большой квадрат разделен на левый и правый прямоугольники. Строится треугольник, который имеет половину площади левого прямоугольника. Затем строится еще один треугольник, который имеет половину площади квадрата с левой стороны. Эти два треугольника показаны как конгруэнтный, доказывая, что этот квадрат имеет ту же площадь, что и левый прямоугольник. За этим аргументом следует аналогичная версия для правого прямоугольника и оставшегося квадрата. Если сложить два прямоугольника вместе, чтобы преобразовать квадрат на гипотенузе, его площадь будет равна сумме площадей двух других квадратов. Подробности приведены ниже.
Позволять А, B, C быть вершины прямоугольного треугольника с прямым углом при А. Отбросьте перпендикуляр из А в сторону, противоположную гипотенузе, в квадрате на гипотенузе. Эта линия делит квадрат гипотенузы на два прямоугольника, каждый из которых имеет такую же площадь, что и один из двух квадратов на катетах.
Для формального доказательства нам потребуются четыре элементарных лемматы:
- Если у двух треугольников две стороны одного равны двум сторонам другого, каждый к каждому, и углы, составляемые этими сторонами, равны, то треугольники равны (сторона угол сторона ).
- Площадь треугольника равна половине площади любого параллелограмма на том же основании и на той же высоте.
- Площадь прямоугольника равна произведению двух смежных сторон.
- Площадь квадрата равна произведению двух его сторон (следует из 3).
Затем каждый верхний квадрат связан с треугольником, совпадающим с другим треугольником, связанным, в свою очередь, с одним из двух прямоугольников, составляющих нижний квадрат.[8]
Иллюстрация с новыми линиями
Показаны два конгруэнтных треугольника половиной площади прямоугольника BDLK и квадрата BAGF.
Доказательство таково:
- Пусть ACB — прямоугольный треугольник с прямым углом CAB.
- На каждой из сторон BC, AB и CA нарисованы квадраты CBDE, BAGF и ACIH в указанном порядке. Построение квадратов требует непосредственно предшествующих теорем Евклида и зависит от постулата параллельности.[9]
- От A проведите линию, параллельную BD и CE. Он будет перпендикулярно пересекать BC и DE в точках K и L соответственно.
- Соедините CF и AD, чтобы сформировать треугольники BCF и BDA.
- Углы CAB и BAG — прямые; поэтому C, A и G являются коллинеарен. Аналогично для B, A и H.
- Углы CBD и FBA являются прямыми углами; следовательно, угол ABD равен углу FBC, поскольку оба являются суммой прямого угла и угла ABC.
- Поскольку AB равно FB, а BD равно BC, треугольник ABD должен быть конгруэнтен треугольнику FBC.
- Поскольку AKL — прямая линия, параллельная BD, то прямоугольник BDLK имеет удвоенную площадь треугольника ABD, потому что они имеют общую основу BD и имеют одинаковую высоту BK, т. Е. Прямую, перпендикулярную их общему основанию, соединяющую параллельные прямые BD и AL. (лемма 2)
- Поскольку C коллинеарен с A и G, квадрат BAGF должен быть в два раза больше треугольника FBC.
- Следовательно, прямоугольник BDLK должен иметь такую же площадь, что и квадрат BAGF = AB.2.
- Аналогичным образом можно показать, что прямоугольник CKLE должен иметь такую же площадь, что и квадрат ACIH = AC.2.
- Складывая эти два результата, AB2 + AC2 = BD × BK + KL × KC
- Поскольку BD = KL, BD × BK + KL × KC = BD (BK + KC) = BD × BC
- Следовательно, AB2 + AC2 = BC2, поскольку CBDE — квадрат.
Это доказательство, которое появляется у Евклида. Элементы как предложение 47 книги 1,[10] демонстрирует, что площадь квадрата на гипотенузе равна сумме площадей двух других квадратов.[11] Это совершенно отличается от доказательства по подобию треугольников, которое, как предполагается, является доказательством, которое использовал Пифагор.[7][12]
Доказательства рассечением и перестановкой
Мы уже обсуждали доказательство Пифагора, которое было доказательством путем перестановки. Ту же идею передает самая левая анимация ниже, которая состоит из большого квадрата со стороной а + б, содержащий четыре одинаковых прямоугольных треугольника. Треугольники показаны в двух вариантах, при первом из которых остается два квадрата. а2 и б2 непокрытый, второй из которых оставляет квадрат c2 раскрытый. Площадь, охватываемая внешним квадратом, никогда не изменяется, а площади четырех треугольников одинаковы в начале и в конце, поэтому площади черных квадратов должны быть равны, поэтому а2 + б2 = c2.
Второе доказательство перестановки дается средней анимацией. Образуется большой квадрат площадью c2, из четырех одинаковых прямоугольных треугольников со сторонами а, б и c, расположенный вокруг небольшой центральной площади. Затем формируются два прямоугольника со сторонами а и б перемещая треугольники. Объединение меньшего квадрата с этими прямоугольниками дает два квадрата площадей. а2 и б2, который должен иметь ту же площадь, что и исходный большой квадрат.[13]
Третье, крайнее правое изображение также дает доказательство. Два верхних квадрата разделены, как показано синей и зеленой штриховкой, на части, которые при перестановке могут быть помещены в нижний квадрат на гипотенузе — или, наоборот, большой квадрат можно разделить, как показано, на части, заполняющие два других. . Такой способ разрезания одной фигуры на части и их перестановки для получения другой фигуры называется рассечение. Это показывает, что площадь большого квадрата равна площади двух меньших.[14]
|
Анимация, демонстрирующая доказательство перестановкой четырех одинаковых прямоугольных треугольников |
Анимация, показывающая еще одно доказательство перестановки |
Доказательство с использованием сложной перестановки |
Доказательство Эйнштейна путем препарирования без перестановок
Прямоугольный треугольник на гипотенузе, разрезанный на два подобных прямоугольных треугольника на катетах, согласно доказательству Эйнштейна
Альберт Эйнштейн дал доказательство путем вскрытия, при котором части не нужно двигать.[15] Вместо квадрата на гипотенузе и двух квадратов на катетах можно использовать любую другую форму, которая включает гипотенузу, и два аналогичный формы, каждая из которых включает одно из двух катетов вместо гипотенузы (см. Подобные фигуры с трех сторон ). В доказательстве Эйнштейна фигура, включающая гипотенузу, — это сам прямоугольный треугольник. Рассечение состоит в опускании перпендикуляра из вершины прямого угла треугольника к гипотенузе, таким образом разбивая весь треугольник на две части. Эти две части имеют ту же форму, что и исходный прямоугольный треугольник, и имеют катеты исходного треугольника в качестве гипотенузы, а сумма их площадей равна площади исходного треугольника. Поскольку отношение площади прямоугольного треугольника к квадрату его гипотенузы одинаково для аналогичных треугольников, соотношение между площадями трех треугольников сохраняется и для квадратов сторон большого треугольника.
Алгебраические доказательства
Схема двух алгебраических доказательств
Теорема может быть доказана алгебраически, используя четыре копии прямоугольного треугольника со сторонами а, б и c, расположенный внутри квадрата со стороной c как в верхней половине диаграммы.[16] Треугольники похожи по площади 
Но это квадрат со стороной c и площадь c2, так
В аналогичном доказательстве используются четыре копии одного и того же треугольника, расположенные симметрично вокруг квадрата со стороной c, как показано в нижней части диаграммы.[17] В результате получается квадрат большего размера со стороной а + б и площадь (а + б)2. Четыре треугольника и квадратная сторона c должен иметь такую же площадь, как и большой квадрат,
давая
Схема доказательства Гарфилда
Соответствующее доказательство было опубликовано будущим президентом США. Джеймс А. Гарфилд (потом Представитель США ) (см. диаграмму).[18][19][20] Вместо квадрата используется трапеция, который можно построить из квадрата во втором из приведенных выше доказательств путем деления пополам по диагонали внутреннего квадрата, чтобы получить трапецию, как показано на диаграмме. В площадь трапеции можно рассчитать как половину площади квадрата, то есть
Внутренний квадрат так же делится пополам, и есть только два треугольника, поэтому доказательство продолжается, как указано выше, за исключением множителя 
Доказательство с использованием дифференциалов
К теореме Пифагора можно прийти, изучив, как изменение стороны вызывает изменение гипотенузы, и применив исчисление.[21][22][23]
Треугольник ABC прямоугольный треугольник, как показано в верхней части диаграммы, с до н.э гипотенуза. При этом длины треугольников измеряются, как показано на рисунке, с гипотенузой длины. у, сторона AC длины Икс и сторона AB длины а, как показано в нижней части диаграммы.
Схема для дифференциального доказательства
Если Икс увеличивается на небольшую величину dx расширяя сторону AC слегка к D, тогда у также увеличивается на dy. Они образуют две стороны треугольника, CDE, который (с E выбрал так CE перпендикулярна гипотенузе) представляет собой прямоугольный треугольник, примерно похожий на ABC. Следовательно, соотношение сторон у них должно быть одинаковым, то есть:
Это можно переписать как 
давая
Константу можно вывести из Икс = 0, у = а дать уравнение
Это скорее интуитивное доказательство, чем формальное: его можно сделать более строгим, если использовать правильные ограничения вместо dx и dy.
Converse
В разговаривать теоремы также верны:[24]
Для любых трех положительных чисел а, б, и c такой, что а2 + б2 = c2, существует треугольник со сторонами а, б и c, и каждый такой треугольник имеет прямой угол между сторонами длин а и б.
Альтернативное утверждение:
Для любого треугольника со сторонами а, б, c, если а2 + б2 = c2, тогда угол между а и б измеряет 90 °.
Это обратное также встречается у Евклида. Элементы (Книга I, предложение 48):[25]
«Если в треугольнике квадрат на одной из сторон равен сумме квадратов на оставшихся двух сторонах треугольника, тогда угол, содержащийся между оставшимися двумя сторонами треугольника, будет прямым».
Это можно доказать с помощью закон косинусов или следующим образом:
Позволять ABC быть треугольником со сторонами а, б, и c, с участием а2 + б2 = c2. Постройте второй треугольник со сторонами длины а и б содержащий прямой угол. По теореме Пифагора следует, что гипотенуза этого треугольника имеет длину c = √а2 + б2, то же, что и гипотенуза первого треугольника. Поскольку стороны обоих треугольников одинаковой длины а, б и c, треугольники конгруэнтный и должны иметь одинаковые углы. Следовательно, угол между сторонами длин а и б в исходном треугольнике — прямой угол.
Вышеприведенное доказательство обратного использует саму теорему Пифагора. Обратное также может быть доказано без предположения теоремы Пифагора.[26][27]
А следствие Обратное утверждение теоремы Пифагора представляет собой простой способ определить, является ли треугольник прямым, тупым или острым, следующим образом. Позволять c быть выбрана самой длинной из трех сторон и а + б > c (иначе нет треугольника согласно неравенство треугольника ). Применяются следующие утверждения:[28]
- Если а2 + б2 = c2, затем треугольник правильный.
- Если а2 + б2 > c2, затем треугольник острый.
- Если а2 + б2 < c2, затем треугольник тупой.
Эдсгер В. Дейкстра высказал это предложение об острых, правильных и тупых треугольниках на этом языке:
- sgn (α + β − γ) = sgn (а2 + б2 − c2),
где α угол противоположный стороне а, β угол противоположный стороне б, γ угол противоположный стороне c, а sgn — это функция знака.[29]
Последствия и использование теоремы
Пифагорейские тройки
Пифагорова тройка состоит из трех натуральных чисел а, б, и c, так что а2 + б2 = c2. Другими словами, тройка Пифагора представляет собой длины сторон прямоугольного треугольника, все три стороны которого имеют целые длины.[1] Такая тройка обычно пишется (а, б, c). Некоторые известные примеры: (3, 4, 5) и (5, 12, 13).
Примитивная тройка Пифагора — это та, в которой а, б и c находятся совмещать (в наибольший общий делитель из а, б и c равно 1).
Ниже приведен список примитивных пифагоровых троек со значениями меньше 100:
- (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)
Взаимная теорема Пифагора
Учитывая прямоугольный треугольник с боков 


в то время взаимная теорема Пифагора[30] или перевернутая теорема Пифагора[31] связывает два ноги 

Уравнение можно преобразовать к
где 



используя наименьшую тройку Пифагора 
где знаменатели — квадраты, а также для семиугольный треугольник чьи стороны 
Несоизмеримая длина
В спираль Феодора: Конструкция для отрезков прямой, длина которых равна квадратному корню из положительного целого числа.
Одно из следствий теоремы Пифагора состоит в том, что отрезки прямой, длина которых равна несоизмеримый (так что соотношение не является рациональное число ) можно построить с помощью линейка и компас. Теорема Пифагора позволяет строить несоизмеримые длины, потому что гипотенуза треугольника связана со сторонами квадратный корень операция.
На рисунке справа показано, как построить линейные сегменты, длина которых пропорциональна квадратному корню из любого положительного целого числа.[33] У каждого треугольника есть сторона (обозначенная цифрой «1»), которая является выбранной единицей измерения. В каждом прямоугольном треугольнике теорема Пифагора устанавливает длину гипотенузы в единицах измерения. Если гипотенуза связана с единицей квадратным корнем из положительного целого числа, которое не является полным квадратом, это реализация длины, несоизмеримой с единицей, например √2, √3, √5 . Подробнее см. Квадратичный иррациональный.
Несоизмеримые длины противоречили концепции пифагорейской школы чисел как только целых чисел. В пифагорейской школе пропорции рассматривались путем сравнения целых кратных общей субъединицы.[34] Согласно одной легенде, Гиппас из Метапонта (ок. 470 г. до н.э.) был утоплен в море за то, что объявил о существовании иррационального или несоизмеримого.[35][36]
Сложные числа
Абсолютное значение комплексного числа z это расстояние р от z к происхождению
Для любого комплексное число
то абсолютная величина или модуль определяется как
Итак, три величины, р, Икс и у связаны уравнением Пифагора,
Обратите внимание, что р определяется как положительное число или ноль, но Икс и у может быть как положительным, так и отрицательным. Геометрически р это расстояние z с нуля или происхождения О в комплексная плоскость.
Это можно обобщить, чтобы найти расстояние между двумя точками, z1 и z2 сказать. Требуемое расстояние определяется выражением
так что снова они связаны версией уравнения Пифагора,
Евклидово расстояние
Формула расстояния в Декартовы координаты выводится из теоремы Пифагора.[37] Если (Икс1, у1) и (Икс2, у2) точки на плоскости, то расстояние между ними, также называемое Евклидово расстояние, дан кем-то
В более общем плане в Евклидово п-Космос, евклидово расстояние между двумя точками, 

Если вместо евклидова расстояния квадрат этого значения ( квадрат евклидова расстояния, или SED), полученное уравнение избегает квадратных корней и представляет собой просто сумму SED координат:
Квадратная форма — гладкая, выпуклая функция обеих точек, и широко используется в теория оптимизации и статистика, составляющие основу наименьших квадратов.
Евклидово расстояние в других системах координат
Если декартовы координаты не используются, например, если полярные координаты используются в двух измерениях или, в более общем смысле, если криволинейные координаты используются формулы, выражающие евклидово расстояние, более сложные, чем теорема Пифагора, но могут быть выведены из нее. Типичный пример, когда расстояние по прямой между двумя точками преобразуется в криволинейные координаты, можно найти в применения полиномов Лежандра в физике. Формулы могут быть обнаружены с помощью теоремы Пифагора с уравнениями, связывающими криволинейные координаты с декартовыми координатами. Например, полярные координаты (р, θ) можно представить как:
Затем две точки с локациями (р1, θ1) и (р2, θ2) разделены расстоянием s:
Выполняя квадраты и объединяя члены, формула Пифагора для расстояния в декартовых координатах производит разделение в полярных координатах как:
используя тригонометрический формулы произведения к сумме. Эта формула является закон косинусов, иногда называемую обобщенной теоремой Пифагора.[38] Исходя из этого результата, для случая, когда радиусы двух местоположений находятся под прямым углом, приложенный угол Δθ = π/2, и восстанавливается форма, соответствующая теореме Пифагора: 
Пифагорейская тригонометрическая идентичность
Подобные прямоугольные треугольники показывают синус и косинус угла θ
В прямоугольном треугольнике со сторонами а, б и гипотенуза c, тригонометрия определяет синус и косинус угла θ между стороной а а гипотенуза как:
Из этого следует:
где последний шаг применяет теорему Пифагора. Это соотношение между синусом и косинусом иногда называют фундаментальным тригонометрическим тождеством Пифагора.[39] В подобных треугольниках соотношение сторон одинаково независимо от размера треугольников и зависит от углов. Следовательно, на рисунке треугольник с гипотенузой единицы размера имеет противоположную сторону размера sinθ и прилегающей стороны размером cosθ в единицах гипотенузы.
Отношение к перекрестному произведению
Площадь параллелограмма как скрещенного произведения; векторов а и б определить самолет и а × б нормально к этой плоскости.
Теорема Пифагора связывает перекрестное произведение и скалярное произведение Аналогичным образом:[40]
Это можно увидеть из определений перекрестного произведения и скалярного произведения, как
с участием п единичный вектор, нормальный к обоим а и б. Связь следует из этих определений и тригонометрического тождества Пифагора.
Это также можно использовать для определения перекрестного произведения. Путем перестановки следующего уравнения получается
Это можно рассматривать как условие для перекрестного произведения и, следовательно, как часть его определения, например, в семь измерений.[41][42]
Обобщения
Подобные фигуры с трех сторон
Обобщение теоремы Пифагора, выходящее за пределы квадратов с трех сторон до похожие цифры был известен Гиппократ Хиосский в V веке до нашей эры,[43] и был включен Евклид в его Элементы:[44]
Если воздвигнуть подобные фигуры (см. Евклидова геометрия ) с соответствующими сторонами на сторонах прямоугольного треугольника, то сумма площадей единиц на двух меньших сторонах равна площади одной на большей стороне.
Это расширение предполагает, что стороны исходного треугольника являются соответствующими сторонами трех конгруэнтных фигур (так что общие отношения сторон подобных фигур равны а: б: в).[45] В то время как доказательство Евклида применимо только к выпуклым многоугольникам, теорема также применима к вогнутым многоугольникам и даже к аналогичным фигурам, которые имеют искривленные границы (но все же с частью границы фигуры, являющейся стороной исходного треугольника).[45]
Основная идея этого обобщения состоит в том, что площадь плоской фигуры равна пропорциональный квадрату любого линейного размера и, в частности, пропорционален квадрату длины любой стороны. Таким образом, если похожие фигуры с площадями А, B и C возводятся по сторонам соответствующей длины а, б и c тогда:
Но по теореме Пифагора а2 + б2 = c2, так А + B = C.
Наоборот, если мы можем доказать, что А + B = C для трех одинаковых фигур без использования теоремы Пифагора мы можем работать в обратном направлении, чтобы построить доказательство теоремы. Например, треугольник начального центра можно воспроизвести и использовать как треугольник. C на его гипотенузе и два подобных прямоугольных треугольника (А и B ), построенный на двух других сторонах, образованный делением центрального треугольника на его высота. Сумма площадей двух меньших треугольников равна площади третьего, таким образом А + B = C и обратная логика приводит к теореме Пифагора a2 + b2 = c2. (Смотрите также Доказательство Эйнштейна путем препарирования без перестановок )
|
Обобщение для подобных треугольников, |
Теорема Пифагора с использованием подобных прямоугольных треугольников |
Обобщение для правильных пятиугольников |
Закон косинусов
Теорема Пифагора — это частный случай более общей теоремы, связывающей длины сторон любого треугольника, закона косинусов:[46]
где 


Когда 


Произвольный треугольник
Обобщение теоремы Пифагора Табит ибн Корра.[47] Нижняя панель: отражение треугольника CAD (вверху) в треугольник DAC, аналогичный треугольнику ABC (вверху).
Под любым выбранным углом общего треугольника сторон а, б, в, впишите равнобедренный треугольник так, чтобы равные углы при его основании θ совпадали с выбранным углом. Предположим, что выбранный угол θ находится напротив стороны, обозначенной c. Начертание равнобедренного треугольника образует треугольник CAD с углом θ противоположной стороны б и со стороны р вместе c. Второй треугольник образован с углом θ противоположной стороны а и сторона с длиной s вместе c, как показано на рисунке. Табит ибн Курра заявил, что стороны трех треугольников связаны следующим образом:[48][49]
По мере приближения угла θ π/ 2 основание равнобедренного треугольника сужается, а длина р и s перекрываются все меньше и меньше. Когда θ = π/2, АБР становится прямоугольным треугольником, р + s = c, и исходная теорема Пифагора восстанавливается.
Одно доказательство отмечает, что треугольник ABC имеет те же углы, что и треугольник CAD, но в обратном порядке. (Два треугольника имеют общий угол в вершине B, оба содержат угол θ, а значит, также имеют одинаковый третий угол постулат треугольника.) Вследствие этого, ABC похоже на отражение CAD, треугольник ЦАП в нижней панели. Принимая соотношение сторон, противоположных и смежных с θ,
Аналогичным образом, для отражения другого треугольника
Очистка фракций и добавляем эти два отношения:
требуемый результат.
Теорема остается в силе, если угол 
Общие треугольники с использованием параллелограммов
Обобщение на произвольные треугольники,
зеленый площадь = синий площадь
Конструкция доказательства обобщения параллелограмма
Теорема площади Паппа является дальнейшим обобщением, которое применяется к треугольникам, которые не являются прямоугольными, с использованием параллелограммов на трех сторонах вместо квадратов (квадраты, конечно, особый случай). На верхнем рисунке показано, что для разностороннего треугольника площадь параллелограмма на самой длинной стороне представляет собой сумму площадей параллелограммов на двух других сторонах, при условии, что параллелограмм на длинной стороне построен, как указано (размеры, отмеченные значком стрелки такие же, и определяют стороны нижнего параллелограмма). Эта замена квадратов параллелограммами имеет явное сходство с исходной теоремой Пифагора и считалась обобщением Папп Александрийский в 4 г. н.э.[50][51]
На нижнем рисунке показаны элементы доказательства. Сосредоточьтесь на левой части фигуры. Левый зеленый параллелограмм имеет ту же площадь, что и левая синяя часть нижнего параллелограмма, потому что оба имеют одинаковое основание. б и высота час. Однако левый зеленый параллелограмм также имеет ту же площадь, что и левый зеленый параллелограмм верхней фигуры, потому что они имеют такое же основание (верхняя левая сторона треугольника) и одинаковую высоту, перпендикулярную этой стороне треугольника. Повторяя рассуждения для правой стороны рисунка, нижний параллелограмм имеет такую же площадь, как сумма двух зеленых параллелограммов.
Твердая геометрия
Теорема Пифагора в трех измерениях связывает диагональ AD с тремя сторонами.
Тетраэдр с прямым углом, обращенным наружу
В терминах твердотельной геометрии теорему Пифагора можно применить к трём измерениям следующим образом. Рассмотрим твердое тело прямоугольной формы, как показано на рисунке. Длина диагонали BD находится из теоремы Пифагора как:
где эти три стороны образуют прямоугольный треугольник. Использование горизонтальной диагонали BD и вертикальный край AB, длина диагонали ОБЪЯВЛЕНИЕ тогда находится вторым применением теоремы Пифагора как:
или, сделав все за один шаг:
Этот результат представляет собой трехмерное выражение для величины вектора v (диагональ AD) через ее ортогональные компоненты {vk} (три взаимно перпендикулярные стороны):
Эту одношаговую формулировку можно рассматривать как обобщение теоремы Пифагора на более высокие измерения. Однако этот результат на самом деле является просто повторным применением исходной теоремы Пифагора к последовательности прямоугольных треугольников в последовательности ортогональных плоскостей.
Существенное обобщение теоремы Пифагора на три измерения: теорема де Гуа, названный в честь Жан Поль де Гуа де Мальв: Если тетраэдр имеет прямой угол (как угол куб ), то квадрат площади грани напротив правого углового угла равен сумме квадратов площадей трех других граней. Этот результат можно обобщить как в «п-мерная теорема Пифагора »:[52]
Позволять
— ортогональные векторы в ℝп. Рассмотрим п-мерный симплекс S с вершинами
. (Подумайте о (п — 1) -мерный симплекс с вершинами
без учета начала координат как «гипотенузы» S а остальные (п — 1) -мерные грани S как его «ноги».) Тогда квадрат объема гипотенузы S это сумма квадратов объемов п ноги.
Это утверждение проиллюстрировано в трех измерениях тетраэдром на рисунке. «Гипотенуза» — это основание тетраэдра в задней части фигуры, а «ноги» — это три стороны, исходящие из вершины на переднем плане. По мере того, как глубина основания от вершины увеличивается, площадь «ног» увеличивается, а площадь основания фиксируется. Теорема предполагает, что когда эта глубина равна значению, создающему правую вершину, применимо обобщение теоремы Пифагора. В другой формулировке:[53]
Учитывая п-прямоугольный п-мерный симплекс, квадрат (п — 1) -содержание грань противостоящая правая вершина будет равна сумме квадратов (п — 1) -содержание остальных граней.
Внутренние пространства продукта
Векторы, участвующие в законе параллелограмма
Теорема Пифагора может быть обобщена на внутренние пространства продукта,[54] которые являются обобщениями известных двумерных и трехмерных Евклидовы пространства. Например, функция можно рассматривать как вектор с бесконечным количеством компонентов во внутреннем пространстве продукта, как в функциональный анализ.[55]
Во внутреннем пространстве продукта концепция перпендикулярность заменяется понятием ортогональность: два вектора v и ш ортогональны, если их внутренний продукт 
Понятие длины заменяется понятием норма ||v|| вектора v, определяется как:[57]
В пространстве внутреннего продукта теорема Пифагора утверждает, что для любых двух ортогональных векторов v и ш у нас есть
Здесь векторы v и ш похожи на стороны прямоугольного треугольника с гипотенузой, заданной векторная сумма v + ш. Эта форма теоремы Пифагора является следствием свойства внутреннего продукта:
где скалярные произведения перекрестных членов равны нулю из-за ортогональности.
Дальнейшим обобщением теоремы Пифагора о внутреннем пространстве продукта на неортогональные векторы является закон параллелограмма :[57]
в котором говорится, что удвоенная сумма квадратов длин сторон параллелограмма равна сумме квадратов длин диагоналей. Любая норма, удовлетворяющая этому равенству, равна ipso facto норма, соответствующая внутреннему продукту.[57]
Тождество Пифагора можно расширить до сумм более двух ортогональных векторов. Если v1, v2, …, vп являются попарно ортогональными векторами в пространстве внутреннего продукта, тогда применение теоремы Пифагора к последовательным парам этих векторов (как описано для 3-х измерений в разделе о сплошная геометрия ) приводит к уравнению[58]
Наборы м-мерные объекты в п-мерное пространство
Другое обобщение теоремы Пифагора применимо к Измеримый по Лебегу наборы объектов в любом количестве измерений. В частности, квадрат меры м-мерный набор объектов в одной или нескольких параллельных м-размерный квартиры в п-размерный Евклидово пространство равна сумме квадратов мер ортогональный проекции объекта (ов) на все м-мерные координатные подпространства.[59]
С математической точки зрения:
где:
Неевклидова геометрия
Теорема Пифагора выводится из аксиом Евклидова геометрия, и фактически, если теорема Пифагора не верна для некоторого прямоугольного треугольника, то плоскость, в которой находится этот треугольник, не может быть евклидовой. Точнее, теорема Пифагора подразумевает и подразумевается параллельным (пятым) постулатом Евклида..[60][61] Таким образом, прямоугольные треугольники в неевклидова геометрия[62]не удовлетворяют теореме Пифагора. Например, в сферическая геометрия, все три стороны прямоугольного треугольника (скажем а, б, и c), ограничивающие октант единичной сферы, имеют длину, равную π/ 2, и все его углы прямые, что нарушает теорему Пифагора, потому что 
Здесь рассматриваются два случая неевклидовой геометрии:сферическая геометрия и геометрия гиперболической плоскости; в каждом случае, как и в евклидовом случае для неправильных треугольников, результат, заменяющий теорему Пифагора, следует из соответствующего закона косинусов.
Однако теорема Пифагора остается верной в гиперболической геометрии и эллиптической геометрии, если условие, что треугольник является прямым, заменяется условием, что два из углов суммируются с третьим, скажем А+B = C. Затем стороны соотносятся следующим образом: сумма площадей окружностей с диаметрами а и б равна площади круга диаметром c.[63]
Сферическая геометрия
Сферический треугольник
Для любого прямоугольного треугольника на сфере радиуса р (например, если γ на рисунке прямой угол), со сторонами а, б, c, соотношение сторон принимает вид:[64]
Это уравнение может быть получено как частный случай сферический закон косинусов это относится ко всем сферическим треугольникам:
Выражая Серия Маклорена для функции косинуса как асимптотическое разложение с оставшимся членом в нотация большой O,
можно показать, что как радиус р приближается к бесконечности и аргументы а / р, б / р, и c / R стремятся к нулю, сферическое соотношение между сторонами прямоугольного треугольника приближается к евклидовой форме теоремы Пифагора. Подставляя асимптотическое разложение для каждого из косинусов в сферическое соотношение для прямоугольного треугольника, получаем
Константы а4, б4, и c4 были поглощены большим О остаточные члены, поскольку они не зависят от радиуса р. Это асимптотическое соотношение можно еще больше упростить, умножив величины в квадратных скобках, отбросив единицы, умножив на −2 и собрав все ошибки вместе:
После умножения на р2, евклидово пифагорейское отношение c2 = а2 + б2 восстанавливается в пределе как радиус р стремится к бесконечности (так как остаточный член стремится к нулю):
Для маленьких прямоугольных треугольников (а, б << р) косинусы можно исключить, чтобы избежать потеря значимости, давая
Гиперболическая геометрия
В гиперболическом пространстве равномерной кривизны −1 /р2, для прямоугольного треугольника с ножками а, б, и гипотенуза c, соотношение сторон принимает вид:[65]
где ch — это гиперболический косинус. Эта формула представляет собой особую форму гиперболический закон косинусов это относится ко всем гиперболическим треугольникам:[66]
с γ угол при вершине, противоположной стороне c.
Используя Серия Маклорена для гиперболического косинуса, шиш Икс ≈ 1 + Икс2/2, можно показать, что по мере того, как гиперболический треугольник становится очень маленьким (т. е. как а, б, и c все стремятся к нулю), гиперболическое соотношение для прямоугольного треугольника приближается к форме теоремы Пифагора.
Для маленьких прямоугольных треугольников (а, б << р), гиперболические косинусы можно исключить, чтобы избежать потеря значимости, давая
Очень маленькие треугольники
Для любой равномерной кривизны K (положительный, нулевой или отрицательный) в очень маленьких прямоугольных треугольниках (|K|а2, |K|б2 << 1) с гипотенузой c, можно показать, что
Дифференциальная геометрия
На бесконечно малом уровне в трехмерном пространстве теорема Пифагора описывает расстояние между двумя бесконечно малыми точками как:
с участием ds элемент расстояния и (dx, dy, дз) компоненты вектора, разделяющего две точки. Такое пространство называется Евклидово пространство. Однако в Риманова геометрия, обобщение этого выражения, полезное для общих координат (не только декартовых) и общих пространств (не только евклидовых), принимает форму:[67]
который называется метрический тензор. (Иногда, злоупотребляя языком, тот же термин применяется к набору коэффициентов гij.) Это может быть функция позиции и часто описывает искривленное пространство. Простым примером является евклидово (плоское) пространство, выраженное в криволинейные координаты. Например, в полярные координаты:
История
Ведутся споры о том, была ли теорема Пифагора открыта один раз или много раз во многих местах, и дата первого открытия не определена, как и дата первого доказательства. Историки месопотамской математики пришли к выводу, что правило Пифагора широко использовалось в Старовавилонский период (20-16 века до нашей эры), более чем за тысячу лет до рождения Пифагора.[69][70][71][72] Историю теоремы можно разделить на четыре части: знание Пифагорейские тройки, знание взаимоотношений между сторонами прямоугольный треугольник, знание отношений между смежными углами и доказательства теоремы в рамках некоторой дедуктивной системы.
Написанный между 2000 и 1786 годами до нашей эры, Поднебесная Египтянин Берлинский папирус 6619 включает проблему, решением которой является Пифагорейская тройка 6: 8: 10, но проблема не касается треугольника. В Месопотамский планшет Плимптон 322, написано между 1790 и 1750 годами до нашей эры во время правления Хаммурапи Великий, содержит множество записей, тесно связанных с пифагорейскими тройками.
В Индия, то Баудхаяна Шульба Сутра, даты которых приводятся по-разному — между VIII и V веками до нашей эры,[73] содержит список Пифагорейские тройки и утверждение теоремы Пифагора, как в частном случае равнобедренный прямоугольный треугольник и в общем случае, как и Апастамба Шульба Сутра (ок. 600 г. до н. э.). Ван дер Варден считал, что этот материал «определенно основан на более ранних традициях». Карл Бойер утверждает, что теорема Пифагора в Шулба-сутрам Возможно, на него повлияла древняя месопотамская математика, но убедительных доказательств в пользу или против такой возможности нет.[74]
Прокл в пятом веке нашей эры утверждает два арифметических правила, «одно из них приписывается Платону, другое — Пифагору»,[75] для генерации специальных пифагоровых троек. Правило, приписываемое Пифагор (c. 570 — c. 495 г. до н.э.) начинается с нечетного числа и дает тройку с катетом и гипотенузой, отличающимися на одну единицу; правило, приписываемое Платон (428/427 или 424/423 — 348/347 до н.э.)) начинается с четного числа и дает тройку с катетом и гипотенузой, различающимися на две единицы. Согласно с Томас Л. Хит (1861–1940 гг.), В сохранившейся греческой литературе за пять веков после жизни Пифагора не существует конкретного приписывания этой теоремы Пифагору.[76] Однако когда такие авторы, как Плутарх и Цицерон приписали теорему Пифагору, они сделали это таким образом, который предполагает, что эта атрибуция была широко известной и несомненной.[77][78] «Независимо от того, правильно ли эта формула приписана лично Пифагору, […] можно смело предположить, что она принадлежит к самому древнему периоду пифагорейской математики».[36] Около 300 г. до н.э., в Евклида Элементы, самый старый из сохранившихся аксиоматическое доказательство теоремы.[79]
С содержанием, известным намного раньше, но в сохранившихся текстах, датируемых примерно I веком до нашей эры, Китайский текст Чжуби Суаньцзин (周 髀 算 经), (Классическая арифметика гномона и круговых путей неба) дает обоснование теоремы Пифагора для треугольника (3, 4, 5) — в Китае он называется «Теорема Гоугу«(勾股定理).[80][81] В течение династия Хан (202 г. до н.э. — 220 г. н.э.), пифагорейские тройки появляются в Девять глав математического искусства,[82] вместе с упоминанием прямоугольных треугольников.[83] Некоторые считают, что теорема впервые возникла в Китай,[84] где он также известен как «Теорема Шан Гао«(中 高 定理),[85] назван в честь астронома и математика герцога Чжоу, чьи рассуждения составили большую часть того, что было в Чжуби Суаньцзин.[86]
Смотрите также
- Теорема британского флага
- В Дулькарноне
- Последняя теорема Ферма
- Обратная теорема Пифагора
- Треугольник Кеплера
- Линейная алгебра
- Список тем треугольника
- Lп Космос
- Число негипотенузы
- Закон параллелограмма
- Теорема Птолемея
- Пифагорейское ожидание
- Пифагорейская черепица
- Рациональная тригонометрия в теореме Пифагора
Заметки
- ^ а б Джудит Д. Салли; Пол Салли (2007). «Глава 3: Пифагорейские тройки». Истоки исследования: вертикальное развитие математических задач. Книжный магазин Американского математического общества. п. 63. ISBN 978-0-8218-4403-8.
- ^ Бенсон, Дональд. Момент доказательства: математические прозрения, стр. 172–173 (Oxford University Press, 1999).
- ^ Евклид (1956), стр. 351–352
- ^ Хаффман, Карл. «Пифагор». В Залта, Эдуард Н. (ред.). Стэнфордская энциклопедия философии (издание зимой 2018 г.).«Теперь должно быть ясно, что решения об источниках имеют решающее значение для решения вопроса о том, был ли Пифагор математиком и ученым. Взгляд на космос Пифагора, изложенный в первых пяти абзацах этого раздела, согласно которому он не был ни математиком, ни ученый, остается консенсусом «.
- ^ (Лумис 1968 )
- ^ (Maor 2007, п.39 )
- ^ а б Стивен В. Хокинг (2005). Бог создал целые числа: математические открытия, изменившие историю. Филадельфия: Издательство Running Press Book Publishers. п. 12. ISBN 0-7624-1922-9.Это доказательство впервые появилось после того, как компьютерная программа была настроена для проверки евклидовых доказательств.
- ^ См. Например Теорема Пифагора по отображению сдвига В архиве 2016-10-14 на Wayback Machine, Java-апплет веб-сайта Университета Сент-Луиса
- ^ Ян Гуллберг (1997). Математика: от рождения чисел. W. W. Norton & Company. п.435. ISBN 0-393-04002-X.
- ^ Элементы 1.47 пользователя Euclid. Проверено 19 декабря 2006 года.
- ^ Элементы Евклида, книга I, предложение 47: версия веб-страницы с использованием Java-апплетов из Элементы Евклида Профессор Дэвид Э. Джойс, Университет Кларка
- ^ Доказательство Пифагора, вероятно, не было общим, поскольку теория пропорций была разработана всего через два столетия после Пифагора; увидеть (Maor 2007, п.25 )
- ^ Александр Богомольный. «Теорема Пифагора, доказательство № 10». Разрежьте узел. Получено 27 февраля 2010.
- ^ (Лумис 1968, п. 113, геометрическое доказательство 22 и рисунок 123)
- ^ Шредер, Манфред Роберт (2012). Фракталы, хаос, степенные законы: минуты из бесконечного рая. Курьерская корпорация. С. 3–4. ISBN 978-0486134789.CS1 maint: ref = harv (ссылка на сайт)
- ^ Александр Богомольный. «Cut-the-knot.org: Теорема Пифагора и ее многочисленные доказательства, Доказательство № 3». Разрежьте узел. Получено 4 ноября 2010.
- ^ Александр Богомольный. «Cut-the-knot.org: Теорема Пифагора и ее многочисленные доказательства, Доказательство № 4». Разрежьте узел. Получено 4 ноября 2010.
- ^ Опубликовано в еженедельной математической колонке: Джеймс А. Гарфилд (1876 г.). «Pons Asinorum». Образовательный журнал Новой Англии. 3 (14): 161.CS1 maint: ref = harv (ссылка на сайт) как отмечено в Уильям Данэм (1997). Математическая вселенная: путешествие по алфавиту через великие доказательства, проблемы и личности. Вайли. п. 96. ISBN 0-471-17661-3. И в Календарь математических дат: 1 апреля 1876 г. В архиве 14 июля 2010 г. Wayback Machine В. Фредерик Рики
- ^ Ланц, Дэвид. «Доказательство Гарфилда теоремы Пифагора». Math.Colgate.edu. Архивировано из оригинал на 2013-08-28. Получено 2018-01-14.
- ^ Маор, Эли, Теорема Пифагора, Princeton University Press, 2007: стр. 106-107.
- ^ Майк Стинг (1996). «Пифагорейское предложение: доказательство с помощью исчисления». Математический журнал. Математическая ассоциация Америки. 69 (1): 45–46. Дои:10.2307/2691395. JSTOR 2691395.CS1 maint: ref = harv (ссылка на сайт)
- ^ Богомольный Александр. «Теорема Пифагора». Интерактивная математика и головоломки. Александр Богомольный. Архивировано из оригинал на 2010-07-06. Получено 2010-05-09.
- ^ Брюс С. Берндт (1988). «Рамануджан — 100 лет (вылепленный) или 100 лет новый (фантазийный)?». Математический интеллект. 10 (3): 24–31. Дои:10.1007 / BF03026638. S2CID 123311054.CS1 maint: ref = harv (ссылка на сайт)
- ^ Джудит Д. Салли; Пол Дж. Салли младший (21 декабря 2007 г.). «Теорема 2.4 (обратная теореме Пифагора)».. Корни исследования. Американское математическое общество. С. 54–55. ISBN 978-0-8218-4403-8.
- ^ Элементы Евклида, книга I, предложение 48 От D.E. Веб-страница Джойса в университете Кларка
- ^ Кейси, Стивен, «Обратное теоремы Пифагора», Математический вестник 92, июль 2008 г., 309–313.
- ^ Митчелл, Дуглас В., «Отзыв о 92.47», Математический вестник 93, март 2009 г., стр. 156.
- ^ Эрнест Юлиус Вильчинский; Герберт Эллсуорт Слут (1914). «Теорема 1 и теорема 2». Плоская тригонометрия и приложения. Аллин и Бэкон. п.85.
- ^ Дейкстра, Эдсгер В. (7 сентября 1986 г.). «О теореме Пифагора». EWD975. Архив Э. В. Дейкстры.
- ^ Р. Б. Нельсен, Доказательство без слов: взаимная теорема Пифагора, Mathematics Magazine, 82, декабрь 2009 г., с. 370
- ^ Перевернутая теорема Пифагора, Дженнифер Ричиник, The Mathematical Gazette, Vol. 92, № 524 (июль 2008 г.), стр. 313-316
- ^ Александр Богомольный, Теорема Пифагора для взаимных чисел,https://www.cut-the-knot.org/pythagoras/PTForReciprocals.shtml
- ^ Закон, Генри (1853). «Следствие 5 предложения XLVII (Теорема Пифагора)». Элементы Евклида: со многими дополнительными предложениями и пояснительными примечаниями, к которым добавляется вводное эссе по логике.. Джон Уил. п. 49.
- ^ Шауган Лавин (1994). Понимание бесконечного. Издательство Гарвардского университета. п. 13. ISBN 0-674-92096-1.
- ^ (Хит 1921, Vol I, pp. 65); Гиппас в то время был в плавании, и его товарищи выбросили его за борт. Увидеть Джеймс Р. Чойк (1980). «Пентаграмма и открытие иррационального числа». Математический журнал колледжа. 11: 312–316.CS1 maint: ref = harv (ссылка на сайт)
- ^ а б Тщательное обсуждение вклада Гиппаса можно найти вКурт фон Фриц (апрель 1945 г.). «Открытие несоизмеримости Гиппасом из Метапонта». Анналы математики. Вторая серия. 46 (2): 242–264. Дои:10.2307/1969021. JSTOR 1969021.CS1 maint: ref = harv (ссылка на сайт)
- ^ Джон Орвант; Яркко Хиетаниеми; Джон Макдональд (1999). «Евклидово расстояние». Освоение алгоритмов с помощью Perl. O’Reilly Media, Inc. стр. 426. ISBN 1-56592-398-7.
- ^ Вентворт, Джордж (2009). Плоская тригонометрия и таблицы. БиблиоБазар, ООО. п. 116. ISBN 978-1-103-07998-8., Упражнения, стр.116
- ^ Лоуренс С. Лефф (2005). Простой способ PreCalculus (7-е изд.). Образовательная серия Бэррона. п.296. ISBN 0-7641-2892-2.
- ^ WS Massey (декабрь 1983 г.). «Перекрестные произведения векторов в многомерных евклидовых пространствах». Американский математический ежемесячник. Математическая ассоциация Америки. 90 (10): 697–701. Дои:10.2307/2323537. JSTOR 2323537.CS1 maint: ref = harv (ссылка на сайт)
- ^ Пертти Лаунесто (2001). «§7.4 Перекрестное произведение двух векторов». Алгебры Клиффорда и спиноры (2-е изд.). Издательство Кембриджского университета. п. 96. ISBN 0-521-00551-5.
- ^ Фрэнсис Бегно Хильдебранд (1992). Методы прикладной математики (Перепечатка Prentice-Hall 1965, 2-е изд.). Courier Dover Publications. п. 24. ISBN 0-486-67002-3.
- ^ Хит, Т. Л., История греческой математики, Oxford University Press, 1921; перепечатано Dover, 1981.
- ^ Евклида Элементы: Книга VI, Предложение VI 31: «В прямоугольных треугольниках фигура на стороне, образующей прямой угол, равна аналогичным и аналогичным образом описанным фигурам на сторонах, содержащих прямой угол».
- ^ а б Пуц, Джон Ф. и Сипка, Тимоти А. «Об обобщении теоремы Пифагора», Математический журнал колледжа 34 (4), сентябрь 2003 г., стр. 291–295.
- ^ Лоуренс С. Лефф (2005-05-01). цитируемая работа. Образовательная серия Бэррона. п. 326. ISBN 0-7641-2892-2.
- ^ Говард Уитли Ивс (1983). «§4.8: … обобщение теоремы Пифагора». Великие моменты в математике (до 1650 г.). Математическая ассоциация Америки. п.41. ISBN 0-88385-310-8.
- ^ Айдын Сайили (март 1960 г.). «Обобщение теоремы Пифагора Табита ибн Курры». Исида. 51 (1): 35–37. Дои:10.1086/348837. JSTOR 227603.CS1 maint: ref = harv (ссылка на сайт)
- ^ Джудит Д. Салли; Пол Салли (21 декабря 2007 г.). «Упражнение 2.10 (ii)». Корни исследования: вертикальное развитие математических проблем. п. 62. ISBN 978-0-8218-4403-8.
- ^ Подробнее о такой конструкции см. Джордж Дженнингс (1997). «Рисунок 1.32: Обобщенная теорема Пифагора». Современная геометрия с аппликациями: со 150 фигурами (3-е изд.). Springer. п.23. ISBN 0-387-94222-X.
- ^ Клауди Альсина, Роджер Б. Нельсен: Очаровательные доказательства: путешествие в элегантную математику. МАА, 2010 г., ISBN 9780883853481, стр. 77–78 (выдержка, п. 77, в Google Книги )
- ^ Раджендра Бхатия (1997). Матричный анализ. Springer. п. 21. ISBN 0-387-94846-5.
- ^ Более подробное обсуждение этого обобщения см., Например, в Вилли В. Вонг В архиве 2009-12-29 в Wayback Machine 2002, Обобщенная n-мерная теорема Пифагора.
- ^ Фердинанд ван дер Хейден; Дик де Риддер (2004). Классификация, оценка параметров и оценка состояния. Вайли. п. 357. ISBN 0-470-09013-8.
- ^ Цюнь Линь; Цзяфу Линь (2006). Методы конечных элементов: точность и улучшение. Эльзевир. п. 23. ISBN 7-03-016656-6.
- ^ Говард Антон; Крис Роррес (2010). Элементарная линейная алгебра: прикладная версия (10-е изд.). Вайли. п. 336. ISBN 978-0-470-43205-1.
- ^ а б c Карен Сакс (2002). «Теорема 1.2». Начало функционального анализа. Springer. п. 7. ISBN 0-387-95224-1.
- ^ Дуглас, Рональд Г. (1998). Методы банаховой алгебры в теории операторов (2-е изд.). Нью-Йорк, Нью-Йорк: Springer-Verlag New York, Inc., стр. 60–61. ISBN 978-0-387-98377-6.
- ^ Дональд Р. Конант и Уильям А. Бейер (март 1974 г.). «Обобщенная теорема Пифагора». Американский математический ежемесячник. Математическая ассоциация Америки. 81 (3): 262–265. Дои:10.2307/2319528. JSTOR 2319528.CS1 maint: ref = harv (ссылка на сайт)
- ^ Эрик В. Вайсштейн (2003). CRC краткая энциклопедия математики (2-е изд.). п. 2147. ISBN 1-58488-347-2.
Постулат параллельности эквивалентен Постулат равноудаленности, Аксиома Playfair, Аксиома прокла, то Постулат треугольника и теорема Пифагора.
- ^ Александр Р. Прусс (2006). Принцип достаточной причины: переоценка. Издательство Кембриджского университета. п. 11. ISBN 0-521-85959-X.
Мы могли бы включить … параллельный постулат и вывести теорему Пифагора. Или мы могли бы вместо этого сделать теорему Пифагора среди других аксиом и вывести постулат параллельности.
- ^ Стивен В. Хокинг (2005). цитируемая работа. п. 4. ISBN 0-7624-1922-9.
- ^ Виктор Памбуччян (декабрь 2010 г.). «Гиперболическая теорема Пифагора Марии Терезы Калапсо». Математический интеллект. 32 (4): 2. Дои:10.1007 / s00283-010-9169-0.
- ^ Барретт О’Нил (2006). «Упражнение 4». Элементарная дифференциальная геометрия (2-е изд.). Академическая пресса. п. 441. ISBN 0-12-088735-5.
- ^ Саул Шталь (1993). «Теорема 8.3». Полуплоскость Пуанкаре: ворота в современную геометрию. Джонс и Бартлетт Обучение. п. 122. ISBN 0-86720-298-X.
- ^ Джейн Гилман (1995). «Гиперболические треугольники». Дискретные подгруппы с двумя образующими в PSL (2, R). Книжный магазин Американского математического общества. ISBN 0-8218-0361-1.
- ^ Тай Л. Чоу (2000). Математические методы для физиков: краткое введение. Издательство Кембриджского университета. п. 52. ISBN 0-521-65544-7.
- ^ Нойгебауэр 1969, п. 36.
- ^ Нойгебауэр 1969: п. 36 «Другими словами, на протяжении всей вавилонской математики было известно, что сумма квадратов длин сторон прямоугольного треугольника равна квадрату длины гипотенузы».
- ^ Фриберг, Йоран (1981). «Методы и традиции вавилонской математики: Плимптон 322, пифагорейские тройки и уравнения параметров вавилонского треугольника». Historia Mathematica. 8: 277–318. Дои:10.1016/0315-0860(81)90069-0.: п. 306 «Хотя« Плимптон 322 »- уникальный текст в своем роде, существует несколько других известных текстов, свидетельствующих о том, что теорема Пифагора была хорошо известна математикам древневавилонского периода».
- ^ Хёйруп, Йенс. «Правило Пифагора и теорема — зеркало отношения между вавилонской и греческой математикой». В Renger, Johannes (ред.). Вавилон: Focus mesopotamischer Geschichte, Wiege früher Gelehrsamkeit, Mythos in der Moderne. 2. Internationales Colloquium der Deutschen Orient-Gesellschaft 24.–26. Мэрц 1998 в Берлине (PDF). Берлин: Deutsche Orient-Gesellschaft / Саарбрюккен: SDV Saarbrücker Druckerei und Verlag. С. 393–407., п. 406, «Судить только по этим свидетельствам поэтому вероятно, что правило Пифагора было обнаружено в среде непрофессиональных геодезистов, возможно, как побочный результат проблемы, рассматриваемой в Db.2-146, где-то между 2300 и 1825 гг. До н.э. «(Db2-146 это древневавилонская глиняная табличка из Эшнунна относительно вычисления сторон прямоугольника с учетом его площади и диагонали.)
- ^ Робсон, Э. (2008). Математика в Древнем Ираке: социальная история. Издательство Принстонского университета.: п. 109 «Многие старовавилонские математики… знали, что квадрат на диагонали прямоугольного треугольника имеет такую же площадь, как сумма квадратов по длине и ширине: это соотношение используется в отработанных решениях текстовых задач на разрезе и -паста «алгебра» на семи разных табличках из Эшнуны, Сиппара, Сузы и неизвестного места в южной Вавилонии ».
- ^ Ким Плофкер (2009). Математика в Индии. Издательство Принстонского университета. С. 17–18, со сноской 13 к Сутре, идентичной теореме Пифагора. ISBN 978-0-691-12067-6.
- ^ Карл Бенджамин Бойер; Ута К. Мерцбах (2011). «Китай и Индия». История математики (3-е изд.). Вайли. п. 229. ISBN 978-0470525487.
Цитата: [В Сульба-сутрах] мы находим правила построения прямых углов с помощью троек нитей, длина которых формирует пифагорейские сортировки, такие как 3, 4 и 5, или 5, 12, 13 или 8, 15 и 17, или 12, 35 и 37. Хотя влияние Месопотамии в Sulvasũtras вполне вероятно, мы не знаем убедительных доказательств за или против этого. Аспастамба знал, что квадрат на диагонали прямоугольника равен сумме квадратов на двух соседних сторонах. Менее легко объяснимо другое правило, данное Апастамбой, которое сильно напоминает геометрическую алгебру из книги II Евклида. Элементы. (…)
- ^ Прокл (1970). Комментарий к первой книге Евклида Элементы. Перевод Морроу, Гленн Р. Принстонский университет. 428,6.
- ^ (Евклид 1956, п. 351) стр. 351
- ^ (Хит 1921, Том I, стр. 144): «Хотя это утверждение повсеместно связывается традицией с именем Пифагора, не существует действительно заслуживающих доверия свидетельств того, что оно было действительно им открыто. Сравнительно поздние авторы, приписывающие его ему, добавляют историю о том, что он принес в жертву вола. отпраздновать его открытие «.
- ^ Обширное обсуждение исторических свидетельств представлено в (Евклид 1956, п. 351) page = 351
- ^ Асгер Обое (1997). Эпизоды из ранней истории математики. Математическая ассоциация Америки. п. 51. ISBN 0-88385-613-1.
… только у Евклида мы находим логическую последовательность общих теорем с соответствующими доказательствами.
- ^ Роберт П. Криз (2008). Великие уравнения: научные открытия от Пифагора до Гейзенберга. W W Norton & Co. стр.25. ISBN 978-0-393-06204-5.
- ^ Довольно обширное обсуждение происхождения различных текстов в Чжоу Би предоставлено Кристофер Каллен (2007). Астрономия и математика в Древнем Китае: «Чжоу Би Суан Цзин». Издательство Кембриджского университета. стр.139 ff. ISBN 978-0-521-03537-8.
- ^ Эта работа представляет собой сборник из 246 задач, некоторые из которых пережили сожжение книг в 213 году до нашей эры и были приведены в окончательную форму до 100 года нашей эры. Это широко комментировал Лю Хуэй в 263 году нашей эры. Филип Д. Стрэффин мл. (2004). «Лю Хуэй и первый золотой век китайской математики». В Марлоу Андерсоне; Виктор Дж. Кац; Робин Дж. Уилсон (ред.). Шерлок Холмс в Вавилоне: и другие истории математики. Математическая ассоциация Америки. стр.69 ff. ISBN 0-88385-546-1. См., В частности, §3: Девять глав по математическому искусству, стр.71 ff.
- ^ Каншен Шен; Джон Н. Кроссли; Энтони Ва-Чунг Лун (1999). Девять глав о математическом искусстве: компаньоны и комментарии. Издательство Оксфордского университета. п. 488. ISBN 0-19-853936-3.
- ^ В частности, Ли Чимин; увидеть Центавр, Том 39. Копенгаген: Мунксгаард. 1997. С. 193, 205.
- ^ Чен, Ченг-И (1996). «§3.3.4 Формула Чен Зо и метод Чонг-Ча; Рисунок 40». Ранние китайские работы в области естествознания: пересмотр физики движения, акустики, астрономии и научных мыслей. Издательство Гонконгского университета. п. 142. ISBN 962-209-385-Х.
- ^ Вэнь-цюнь Ву (2008). «Теорема Гоугу». Избранные произведения Вэнь-цзюнь Ву. World Scientific. п. 158. ISBN 978-981-279-107-8.
использованная литература
- Белл, Джон Л. (1999). Искусство разумного: элементарный обзор математики в ее концептуальном развитии. Kluwer. ISBN 0-7923-5972-0.
- Евклид (1956). Тринадцать книг стихов Евклида, переведенные с текста Хейберга, с введением и комментариями. Vol. 1 (Книги I и II). Перевод Хита, Томаса Л. (Перепечатка 2-го изд. (1925)). Дувр.CS1 maint: ref = harv (ссылка на сайт) Он-лайн текст на archive.org
- Хит, сэр Томас (1921). «Теорема Пифагора»‘«. История греческой математики (2 тома) (Dover Publications, Inc. (1981) изд.). Кларендон Пресс, Оксфорд. стр.144 ff. ISBN 0-486-24073-8.CS1 maint: ref = harv (ссылка на сайт)
- Либескинд, Шломо (2008). Евклидова и трансформационная геометрия: дедуктивное исследование. Джонс и Бартлетт Обучение. ISBN 978-0-7637-4366-6. Этот учебник по геометрии для старших классов охватывает многие темы этой статьи WP.
- Лумис, Элиша Скотт (1968). Предложение Пифагора (2-е изд.). Национальный совет учителей математики. ISBN 978-0-87353-036-1.CS1 maint: ref = harv (ссылка на сайт) Полный текст 2-го издания 1940 г. см. Элиша Скотт Лумис. «Пифагорейское суждение: его демонстрации проанализированы и классифицированы, а также библиография источников данных для четырех видов доказательств» (PDF). Информационный центр образовательных ресурсов. Институт педагогических наук (IES) Департамент образования США. Получено 2010-05-04. Первоначально опубликовано в 1940 г. и переиздано в 1968 г. Национальным советом учителей математики. ISBN 0-87353-036-5.
- Маор, Эли (2007). Теорема Пифагора: 4000-летняя история. Принстон, Нью-Джерси: Издательство Принстонского университета. ISBN 978-0-691-12526-8.CS1 maint: ref = harv (ссылка на сайт)
- Нойгебауэр, Отто (1969). Точные науки в древности. Acta Historica Scientiarum Naturalium et Medicinalium. 9 (Переиздание издательства Brown University Press, 1957 г., 2-е изд.). Courier Dover Publications. С. 1–191. ISBN 0-486-22332-9. PMID 14884919.
- Робсон, Элеонора и Жаклин Стедалл, ред., Оксфордский справочник по истории математики, Оксфорд: Oxford University Press, 2009. С. vii + 918. ISBN 978-0-19-921312-2.
- Стиллвелл, Джон (1989). Математика и ее история. Springer-Verlag. ISBN 0-387-96981-0. Также ISBN 3-540-96981-0.
- Swetz, Франк; Као, Т. I. (1977). Был ли Пифагор китайцем?: Исследование теории прямоугольного треугольника в древнем Китае. Издательство Пенсильванского государственного университета. ISBN 0-271-01238-2.
- ван дер Варден, Бартель Леендерт (1983). Геометрия и алгебра в древних цивилизациях. Springer. ISBN 3-540-12159-5.
Пифагорейские троицы вавилонских писцов ван дер Варден.
CS1 maint: ref = harv (ссылка на сайт)
внешние ссылки
- теорема Пифагора в ProofWiki
- Евклид (1997) [ок. 300 г. до н.э.]. Дэвид Э. Джойс (ред.). Элементы. Получено 2006-08-30. В HTML с интерактивными рисунками на основе Java.
- «Теорема Пифагора». Энциклопедия математики. EMS Press. 2001 [1994].
- Историческая тема: Теорема Пифагора в вавилонской математике
- Интерактивные ссылки:
- Интерактивное доказательство в Ява теоремы Пифагора
- Еще одно интерактивное доказательство в Ява теоремы Пифагора
- теорема Пифагора с интерактивной анимацией
- Анимированные, неалгебраические и ориентированные на пользователя теорема Пифагора
- Демонстрация воды по теореме Пифагора на ютубе
- теорема Пифагора (более 70 доказательств из завязать узел )
- Вайсштейн, Эрик В. «Теорема Пифагора». MathWorld.
Эта статья о классической геометрии. Чтобы узнать о бейсбольном термине, см. Пифагорейское ожидание .
Теорема Пифагора
Сумма площадей двух квадратов на катетах ( a и b ) равна площади квадрата на гипотенузе ( c ).
В математике теорема Пифагора , или теорема Пифагора , является фундаментальным соотношением в евклидовой геометрии между тремя сторонами прямоугольного треугольника . Он гласит, что площадь квадрата, стороной которого является гипотенуза (сторона, противоположная прямому углу ), равна сумме площадей квадратов двух других сторон . Эта теорема может быть записана как уравнение, связывающее длины сторон a , b и c , часто называемое уравнением Пифагора :
где c представляет длину гипотенузы, а a и b длины двух других сторон треугольника. Теорема, история которой является предметом многочисленных споров, названа в честь греческого философа Пифагора , родившегося около 570 г. до н.э.
Теорема была доказана множество раз множеством различных методов — возможно, больше всего для любой математической теоремы. Доказательства разнообразны, включая как геометрические, так и алгебраические доказательства, некоторые из которых датируются тысячами лет.
Теорему можно обобщить различными способами: на многомерные пространства , на пространства, которые не являются евклидовыми , на объекты, которые не являются прямоугольными треугольниками, и на объекты, которые вовсе не треугольники, а n — мерные тела. Теорема Пифагора вызвала интерес за пределами математики как символ математической заумности , загадочности или интеллектуальной силы; популярные упоминания в литературе, пьесах, мюзиклах, песнях, марках и мультфильмах имеются в большом количестве.
Доказательство перестановки
Доказательство перестановки (нажмите, чтобы посмотреть анимацию)
Два больших квадрата, показанные на рисунке, содержат по четыре одинаковых треугольника, и единственная разница между двумя большими квадратами заключается в том, что треугольники расположены по-разному. Следовательно, пустое пространство внутри каждого из двух больших квадратов должно иметь одинаковую площадь. Приравнивание площади белого пространства дает теорему Пифагора, КЭД
Английский математик сэр Томас Хит дает это доказательство в своем комментарии к предложению I.47 в « Элементах» Евклида и упоминает предложения Германа. математиками Карлом Антоном Бретшнайдером и Германом Ганкелем , Пифагор мог знать это доказательство. Сам Хит поддерживает другое предложение пифагорейского доказательства, но признает с самого начала своего обсуждения, «что греческая литература, которой мы располагаем и относящаяся к первым пяти столетиям после Пифагора, не содержит утверждений, определяющих это или какое-либо другое конкретное великое геометрическое открытие, сделанное им. » Недавние исследования ставят под сомнение какую-либо роль Пифагора как создателя математики, хотя споры об этом продолжаются.
Другие формы теоремы
Если c обозначает длину гипотенузы, а a и b обозначают длины двух других сторон, теорему Пифагора можно выразить в виде уравнения Пифагора:
Если известны длины как a, так и b , то c можно рассчитать как
Если известна длина гипотенузы c и одной стороны ( a или b ), то длину другой стороны можно вычислить как
или
Уравнение Пифагора связывает стороны прямоугольного треугольника простым способом, так что, если известны длины любых двух сторон, можно найти длину третьей стороны. Другое следствие теоремы состоит в том, что в любом прямоугольном треугольнике гипотенуза больше любой из других сторон, но меньше их суммы.
Обобщением этой теоремы является закон косинусов , который позволяет вычислить длину любой стороны любого треугольника, зная длины двух других сторон и угол между ними. Если угол между другими сторонами прямой угол, закон косинусов сводится к уравнению Пифагора.
Другие доказательства теоремы
У этой теоремы может быть больше известных доказательств, чем у любой другой ( закон квадратичной взаимности является еще одним претендентом на это различие); книга «Предложение Пифагора » содержит 370 доказательств.
Доказательство с использованием подобных треугольников
Доказательство с использованием подобных треугольников
Это доказательство основано на пропорциональности сторон двух подобных треугольников, то есть на том факте, что отношение любых двух соответствующих сторон подобных треугольников одинаково независимо от размера треугольников.
Пусть ABC представляет собой прямоугольный треугольник с прямым углом , расположенным в точке C , как показано на рисунке. Проведите высоту из точки C и назовите H ее пересечением со стороной AB . Точка H делит длину гипотенузы c на части d и e . Новый треугольник ACH подобен треугольнику ABC , потому что они оба имеют прямой угол (по определению высоты) и имеют общий угол A , а это означает, что третий угол будет одинаковым в обоих треугольниках . отмечен как θ на рисунке. Аналогичным образом треугольник CBH подобен треугольнику ABC . Доказательство подобия треугольников требует постулата треугольника : сумма углов в треугольнике равна двум прямым углам и эквивалентна постулату параллельности . Подобие треугольников приводит к равенству отношений соответствующих сторон:
Первый результат приравнивает косинусы углов θ , тогда как второй результат приравнивает их синусы .
Эти отношения можно записать как
Суммируя эти два равенства, получаем
что после упрощения выражает теорему Пифагора:
Роль этого доказательства в истории является предметом многочисленных спекуляций. Основной вопрос заключается в том, почему Евклид не использовал это доказательство, а изобрел другое. Одна из гипотез состоит в том, что доказательство с помощью подобных треугольников включало теорию пропорций, тему, которая не обсуждалась до более поздних « Элементов », и что в то время теория пропорций нуждалась в дальнейшем развитии.
доказательство Евклида
Доказательство в элементах Евклида
В общих чертах, вот как проходит доказательство в « Началах » Евклида . Большой квадрат разделен на левый и правый прямоугольники. Построен треугольник, площадь которого равна половине площади левого прямоугольника. Затем строится еще один треугольник, крайняя левая сторона которого имеет половину площади квадрата. Показано, что эти два треугольника равны , что доказывает , что этот квадрат имеет ту же площадь, что и левый прямоугольник. За этим аргументом следует аналогичная версия для правого прямоугольника и оставшегося квадрата. Если сложить два прямоугольника вместе, чтобы преобразовать квадрат на гипотенузе, его площадь будет равна сумме площадей двух других квадратов. Подробности следуют.
Пусть А , В , С — вершины прямоугольного треугольника с прямым углом А. Опустить перпендикуляр из точки А на сторону, противоположную гипотенузе, в квадрате на гипотенузе. Эта линия делит квадрат на гипотенузе на два прямоугольника, каждый из которых имеет ту же площадь, что и один из двух квадратов на катетах.
Для формального доказательства нам потребуются четыре элементарные леммы :
- Если у двух треугольников две стороны одного равны двум сторонам другого, каждая каждой из них, и углы между этими сторонами равны, то такие треугольники конгруэнтны ( сторона-угол-сторона ).
- Площадь треугольника равна половине площади любого параллелограмма, имеющего то же основание и ту же высоту.
- Площадь прямоугольника равна произведению двух смежных сторон.
- Площадь квадрата равна произведению двух его сторон (следует из 3).
Затем каждый верхний квадрат связан с треугольником, равным другому треугольнику, связанному, в свою очередь, с одним из двух прямоугольников, составляющих нижний квадрат.
Иллюстрация с новыми линиями
Показаны два конгруэнтных треугольника с половиной площади прямоугольника BDLK и квадрата BAGF.
Доказательство следующее:
- Пусть ACB — прямоугольный треугольник с прямым углом CAB.
- На каждой из сторон BC, AB и CA нарисованы квадраты CBDE, BAGF и ACIH в указанном порядке. Построение квадратов требует непосредственно предшествующих теорем Евклида и зависит от постулата параллельности.
- Из А провести линию, параллельную BD и СЕ. Он будет перпендикулярно пересекать BC и DE в точках K и L соответственно.
- Соедините CF и AD, чтобы сформировать треугольники BCF и BDA.
- Углы CAB и BAG прямые; поэтому C, A и G коллинеарны .
- Углы CBD и FBA прямые; Следовательно, угол ABD равен углу FBC, так как оба являются суммой прямого угла и угла ABC.
- Поскольку AB равен FB, BD равен BC, а угол ABD равен углу FBC, треугольник ABD должен быть равен треугольнику FBC.
- Так как AKL — прямая, параллельная BD, то площадь прямоугольника BDLK вдвое больше площади треугольника ABD, так как они имеют общее основание BD и имеют одинаковую высоту BK, т. е. прямую, перпендикулярную их общему основанию, соединяющую параллельные прямые BD и АЛ. (лемма 2)
- Так как C коллинеарна A и G, а эта прямая параллельна FB, то площадь квадрата BAGF должна быть в два раза больше треугольника FBC.
- Следовательно, прямоугольник BDLK должен иметь ту же площадь, что и квадрат BAGF = AB 2 .
- Применив шаги с 3 по 10 к другой стороне рисунка, можно аналогичным образом показать, что прямоугольник CKLE должен иметь ту же площадь, что и квадрат ACIH = AC 2 .
- Складывая эти два результата, AB 2 + AC 2 = BD × BK + KL × KC
- Так как BD = KL, то BD × BK + KL × KC = BD(BK + KC) = BD × BC
- Следовательно, AB 2 + AC 2 = BC 2 , так как CBDE — квадрат.
Это доказательство, которое появляется в «Элементах» Евклида как доказательство предложения 47 в Книге 1, демонстрирует, что площадь квадрата на гипотенузе есть сумма площадей двух других квадратов. Это совершенно отличается от доказательства подобия треугольников, которое, как предполагается, является доказательством, которое использовал Пифагор.
Доказательства вскрытия и перестановки
Мы уже обсуждали доказательство Пифагора, которое представляло собой доказательство перестановкой. Ту же идею передает самая левая анимация ниже, которая состоит из большого квадрата со стороной a + b , содержащего четыре одинаковых прямоугольных треугольника. Треугольники показаны в двух местах, первое из которых оставляет открытыми два квадрата a 2 и b 2 , второе из которых оставляет незакрытым квадрат c 2 . Площадь, охватываемая внешним квадратом, никогда не меняется, а площадь четырех треугольников одинакова в начале и в конце, поэтому площади черных квадратов должны быть равны, следовательно, a 2 + b 2 = c 2 .
Второе доказательство перестановкой дается средней анимацией. Большой квадрат с площадью c 2 образован четырьмя одинаковыми прямоугольными треугольниками со сторонами a , b и c , расположенными вокруг небольшого центрального квадрата. Затем путем перемещения треугольников образуются два прямоугольника со сторонами a и b . Комбинация меньшего квадрата с этими прямоугольниками дает два квадрата с площадями a 2 и b 2 , которые должны иметь ту же площадь, что и исходный большой квадрат.
Третье, самое правое изображение также дает доказательство. Два верхних квадрата разделены, как показано синей и зеленой штриховкой, на части, которые при перестановке можно сделать так, чтобы они соответствовали нижнему квадрату на гипотенузе, или, наоборот, большой квадрат можно разделить, как показано, на части, которые заполняют два других. . Такой способ разрезания одной фигуры на части и перестановки их для получения другой фигуры называется рассечением . Это показывает, что площадь большого квадрата равна площади двух меньших.
|
Анимация, показывающая доказательство перестановкой четырех одинаковых прямоугольных треугольников. |
Анимация, показывающая другое доказательство перестановкой |
Доказательство с использованием сложной перестановки |
Доказательство Эйнштейна рассечением без перестановки
Прямоугольный треугольник на гипотенузе, разделенный на два подобных прямоугольных треугольника на катетах, согласно доказательству Эйнштейна.
Альберт Эйнштейн представил доказательство методом вскрытия, в котором части не нужно перемещать. Вместо квадрата на гипотенузе и двух квадратов на катетах можно использовать любую другую форму, включающую гипотенузу, и две подобные фигуры, каждая из которых включает один из двух катетов вместо гипотенузы (см. Подобные фигуры на трех сторонах ) . . В доказательстве Эйнштейна фигура, включающая гипотенузу, и есть прямоугольный треугольник. Разрез состоит в опускании перпендикуляра из вершины прямого угла треугольника на гипотенузу, таким образом, весь треугольник расщепляется на две части. Эти две части имеют ту же форму, что и исходный прямоугольный треугольник, и имеют катеты исходного треугольника в качестве гипотенуз, а сумма их площадей равна площади исходного треугольника. Поскольку отношение площади прямоугольного треугольника к квадрату его гипотенузы одинаково для подобных треугольников, соотношение между площадями трех треугольников верно и для квадратов сторон большого треугольника.
Алгебраические доказательства
Схема двух алгебраических доказательств
Теорему можно доказать алгебраически, используя четыре копии прямоугольного треугольника со сторонами a , b и c , расположенные внутри квадрата со стороной c , как в верхней половине диаграммы. Треугольники подобны по площади , а маленький квадрат имеет сторону b − a и площадь ( b − a ) 2 . Следовательно, площадь большого квадрата
Но это квадрат со стороной c и площадью c 2 , поэтому
Аналогичное доказательство использует четыре копии того же треугольника, расположенные симметрично вокруг квадрата со стороной c , как показано в нижней части диаграммы. Это приводит к большему квадрату со стороной a + b и площадью ( a + b ) 2 . Четыре треугольника и сторона квадрата c должны иметь ту же площадь, что и больший квадрат,
давать
Схема доказательства Гарфилда
Соответствующее доказательство было опубликовано будущим президентом США Джеймсом А. Гарфилдом (в то время представителем США ) (см. Диаграмму). Вместо квадрата используется трапеция , которую можно построить из квадрата во втором доказательстве, разделив пополам диагональ внутреннего квадрата, чтобы получить трапецию, как показано на диаграмме. Площадь трапеции можно вычислить как половину площади квадрата, т.
Внутренний квадрат также делится пополам, а треугольников всего два, поэтому доказательство продолжается, как указано выше, за исключением множителя , который удаляется путем умножения на два, чтобы получить результат.
Доказательство с использованием дифференциалов
К теореме Пифагора можно прийти, изучая, как изменения стороны вызывают изменение гипотенузы, и применяя исчисление .
Треугольник ABC прямоугольный, как показано в верхней части диаграммы, с гипотенузой BC . В то же время длины треугольника измеряются, как показано, с гипотенузой длины y , стороной AC длины x и стороной AB длины a , как показано в нижней части диаграммы.
Диаграмма для дифференциального доказательства
Если x увеличить на небольшую величину dx за счет небольшого удлинения стороны AC до D , то y также увеличится на dy . Они образуют две стороны треугольника CDE , который (с E , выбранным таким образом , что CE перпендикулярен гипотенузе) является прямоугольным треугольником, приблизительно подобным ABC . Следовательно, отношения их сторон должны быть одинаковыми, то есть:
Это можно переписать как дифференциальное уравнение , которое можно решить прямым интегрированием:
давать
Константу можно вывести из x = 0, y = a, чтобы получить уравнение
Это скорее интуитивное доказательство, чем формальное: его можно сделать более строгим, если вместо dx и dy использовать соответствующие пределы .
Конверс
Обратное утверждение теоремы также верно:
Для любых трех положительных чисел a , b и c таких, что a 2 + b 2 = c 2 , существует треугольник со сторонами a , b и c , и каждый такой треугольник имеет прямой угол между сторонами длин a и b .
Альтернативное утверждение:
Для любого треугольника со сторонами a , b , c , если a2 + b2 = c2 , то угол между a и b равен 90 ° .
Это обращение также появляется в «Элементах» Евклида (книга I, предложение 48):
«Если в треугольнике квадрат одной из сторон равен сумме квадратов двух оставшихся сторон треугольника, то угол, заключенный между оставшимися двумя сторонами треугольника, прямой».
Это можно доказать с помощью закона косинусов или следующим образом:
Пусть ABC треугольник с длинами сторон a , b и c , причем a 2 + b 2 = c 2 . Постройте второй треугольник со сторонами длины a и b , содержащими прямой угол. По теореме Пифагора следует, что гипотенуза этого треугольника имеет длину c = √ a 2 + b 2 , такую же, как и гипотенуза первого треугольника. Поскольку стороны обоих треугольников имеют одинаковую длину a , b и c , треугольники конгруэнтны и должны иметь одинаковые углы. Следовательно, угол между сторонами длин a и b в исходном треугольнике является прямым углом.
Приведенное выше доказательство обратного использует саму теорему Пифагора. Обратное также можно доказать, не прибегая к теореме Пифагора.
Следствием обратной теоремы Пифагора является простой способ определить, является ли треугольник прямоугольным, тупоугольным или остроугольным, следующим образом. Пусть c выбрано как самая длинная из трех сторон, а a + b > c (иначе не существует треугольника в соответствии с неравенством треугольника ). Применяются следующие утверждения:
- Если a 2 + b 2 = c 2 , то треугольник прямоугольный .
- Если a 2 + b 2 > c 2 , то треугольник остроугольный .
- Если a 2 + b 2 < c 2 , то треугольник тупоугольный .
Эдсгер В. Дейкстра сформулировал это предложение об острых, прямоугольных и тупых треугольниках на этом языке:
- sgn( α + β — γ ) = sgn( a 2 + b 2 — c 2 ),
где α — угол, противолежащий стороне a , β — угол, противолежащий стороне b , γ — угол, противолежащий стороне c , а sign — знаковая функция .
Следствия и использование теоремы
Пифагоровы тройки
Пифагорейская тройка имеет три положительных целых числа a , b и c , такие что a 2 + b 2 = c 2 . Другими словами, пифагорова тройка представляет длины сторон прямоугольного треугольника, где все три стороны имеют целые длины. Такая тройка обычно пишется ( a , b , c ). Некоторые хорошо известные примеры: (3, 4, 5) и (5, 12, 13).
Примитивная пифагорейская тройка — это тройка, в которой a , b и c взаимно просты ( наибольший общий делитель a , b и c равен 1)
.
Ниже приведен список примитивных пифагорейских троек со значениями меньше 100:
- (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12 , 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77) , 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)
Взаимная теорема Пифагора
Дан прямоугольный треугольник со сторонами и высотой (линия, проведенная из прямого угла и перпендикулярная гипотенузе ). Теорема Пифагора имеет,


в то время как обратная теорема Пифагора или перевернутая теорема Пифагора связывает две ноги с высотой ,
Уравнение можно преобразовать к,
где для любого ненулевого действительного . Если должны быть целыми числами , наименьшее решение тогда

используя наименьшую пифагорову тройку . Обратная теорема Пифагора является частным случаем оптического уравнения
где знаменатели — квадраты, а также для семиугольного треугольника , стороны которого — квадратные числа.
Несоизмеримые длины
Спираль Теодора : конструкция для отрезков с длинами, отношения которых являются квадратным корнем из положительного целого числа.
Одним из следствий теоремы Пифагора является то, что отрезки, длины которых несоизмеримы (поэтому отношение которых не является рациональным числом ), можно построить с помощью линейки и циркуля . Теорема Пифагора позволяет строить несоизмеримые длины, потому что гипотенуза треугольника связана со сторонами посредством операции
извлечения квадратного корня .
На рисунке справа показано, как построить отрезки, длина которых находится в отношении квадратного корня из любого положительного целого числа. У каждого треугольника есть сторона (обозначенная цифрой 1), которая является выбранной единицей измерения. В каждом прямоугольном треугольнике теорема Пифагора устанавливает длину гипотенузы в терминах этой единицы. Если гипотенуза связана с единицей квадратным корнем из положительного целого числа, которое не является полным квадратом, это реализация длины, несоизмеримой с единицей, такой как √ 2 , √ 3 , √ 5 . Для получения дополнительной информации см. Квадратичный иррациональный .
Несоизмеримая длина противоречила представлению пифагорейской школы о числах как о целых числах. Пифагорейская школа рассматривала пропорции путем сравнения целых кратных общей субъединицы. Согласно одной легенде, Гиппас из Метапонта ( ок. 470 г. до н. э.) утонул в море за то, что дал понять о существовании иррационального или несоизмеримого.
Сложные числа
Абсолютное значение комплексного числа z — это расстояние r от z до начала координат.
Для любого комплексного числа
абсолютное значение или модуль определяется выражением
Итак, три величины r , x и y связаны уравнением Пифагора:
Обратите внимание, что r определяется как положительное число или нуль, но x и y могут быть как положительными, так и отрицательными. Геометрически r — это расстояние z от нуля или начала координат O в комплексной плоскости .
Это можно обобщить, чтобы найти расстояние между двумя точками, скажем , z 1 и z 2 . Требуемое расстояние определяется выражением
так что снова они связаны версией уравнения Пифагора,
Евклидово расстояние
Формула расстояния в декартовых координатах выводится из теоремы Пифагора. Если ( x 1 , y 1 ) и ( x 2 , y 2 ) являются точками на плоскости, то расстояние между ними, также называемое евклидовым расстоянием , определяется выражением
В более общем смысле, в евклидовом n -пространстве евклидово расстояние между двумя точками и определяется обобщением теоремы Пифагора как:
Если вместо евклидова расстояния используется квадрат этого значения ( квадрат евклидова расстояния или SED), в полученном уравнении не будет квадратных корней, и оно будет просто суммой SED координат:
Квадратная форма представляет собой гладкую выпуклую функцию обеих точек и широко используется в теории оптимизации и статистике , образуя основу метода наименьших квадратов .
Евклидово расстояние в других системах координат
Если декартовы координаты не используются, например, если используются полярные координаты в двух измерениях или, в более общем плане, если используются криволинейные координаты , формулы, выражающие евклидово расстояние, более сложны, чем теорема Пифагора, но могут быть получены из Это. Типичный пример, когда прямолинейное расстояние между двумя точками преобразуется в криволинейные координаты, можно найти в приложениях полиномов Лежандра в физике . Формулы могут быть обнаружены с помощью теоремы Пифагора с уравнениями, связывающими криволинейные координаты с декартовыми координатами. Например, полярные координаты ( r , θ ) могут быть представлены как:
Тогда две точки с положениями ( r 1 , θ 1 ) и ( r 2 , θ 2 ) разделены расстоянием s :
Выполняя квадраты и комбинируя термины, формула Пифагора для расстояния в декартовых координатах дает разделение в полярных координатах как:
используя тригонометрические формулы произведения на сумму . Эта формула представляет собой закон косинусов , иногда называемый обобщенной теоремой Пифагора. Из этого результата для случая, когда радиусы двух точек находятся под прямым углом, замкнутый угол Δ θ = π / 2, и форма, соответствующая теореме Пифагора, восстанавливается: теорема Пифагора, действительная для прямоугольных треугольников, поэтому является частным случаем более общего закона косинусов, справедливого для произвольных треугольников.
Пифагорейское тригонометрическое тождество
Подобные прямоугольные треугольники, показывающие синус и косинус угла θ
В прямоугольном треугольнике со сторонами a , b и гипотенузой c тригонометрия определяет синус и косинус угла θ между стороной a и гипотенузой как:
Отсюда следует:
где последний шаг применяет теорему Пифагора. Это соотношение между синусом и косинусом иногда называют фундаментальным тригонометрическим тождеством Пифагора. В подобных треугольниках отношения сторон одинаковы независимо от размера треугольников и зависят от углов. Следовательно, на рисунке треугольник с гипотенузой единичного размера имеет противолежащую сторону размера sin θ и прилежащую сторону размера cos θ в единицах гипотенузы.
Отношение к перекрестному произведению
Площадь параллелограмма как векторное произведение; векторы a и b определяют плоскость, а a × b нормальна к этой плоскости.
Теорема Пифагора связывает перекрестное произведение и скалярное произведение аналогичным образом:
Это видно из определений перекрестного произведения и скалярного произведения, как
где n единичный вектор, нормальный как к a, так и к b . Связь следует из этих определений и пифагорейского тригонометрического тождества.
Это также можно использовать для определения перекрестного произведения. Путем перестановки следующего уравнения получается
Это можно рассматривать как условие для перекрестного произведения и, таким образом, часть его определения, например, в семи измерениях .
Обобщения
Одинаковые фигуры с трех сторон
Обобщение теоремы Пифагора, распространяющееся за пределы площади квадратов с трех сторон на аналогичные фигуры, было известно Гиппократу Хиосскому в 5 веке до нашей эры и было включено Евклидом в его « Элементы » :
Если построить подобные фигуры (см. Евклидову геометрию ) с соответствующими сторонами на сторонах прямоугольного треугольника, то сумма площадей фигур на двух меньших сторонах равна площади фигур на большей стороне.
Это расширение предполагает, что стороны исходного треугольника являются соответствующими сторонами трех конгруэнтных фигур (таким образом, обычные отношения сторон между подобными фигурами равны a:b:c ). Хотя доказательство Евклида применялось только к выпуклым многоугольникам, теорема также применима к вогнутым многоугольникам и даже к подобным фигурам с изогнутыми границами (но все же с частью границы фигуры, являющейся стороной исходного треугольника).
Основная идея этого обобщения состоит в том, что площадь плоской фигуры пропорциональна квадрату любого линейного размера и, в частности, пропорциональна квадрату длины любой стороны. Таким образом, если подобные фигуры с площадями А , В и С воздвигнуть на сторонах с соответствующими длинами а , b и с , то:
Но по теореме Пифагора a 2 + b 2 = c 2 , поэтому A + B = C .
И наоборот, если мы можем доказать, что A + B = C для трех одинаковых фигур, не используя теорему Пифагора, то мы можем работать в обратном направлении, чтобы построить доказательство теоремы. Например, треугольник с начальным центром можно воспроизвести и использовать как треугольник C на его гипотенузе, а два подобных прямоугольных треугольника ( A и B ) построить на двух других сторонах, образованных делением центрального треугольника на его высоту . Таким образом, сумма площадей двух меньших треугольников равна площади третьего, таким образом, A + B = C , и обращение приведенной выше логики приводит к теореме Пифагора a 2 + b 2 = c 2 . ( См. Также доказательство Эйнштейна путем рассечения без перестановки )
|
Обобщение для подобных треугольников, |
Теорема Пифагора об использовании подобных прямоугольных треугольников |
Обобщение для правильных пятиугольников |
Закон косинусов
Теорема Пифагора является частным случаем более общей теоремы о длинах сторон любого треугольника, закона косинусов:
где угол между сторонами и .
Когда радианы или 90°, то и формула сводится к обычной теореме Пифагора
.
Произвольный треугольник
Обобщение теоремы Пифагора Табитом ибн Корра . Нижняя панель: отражение треугольника CAD (вверху) с образованием треугольника DAC, аналогичного треугольнику ABC (вверху).
В любой выбранный угол общего треугольника со сторонами a, b, c вписать равнобедренный треугольник так, чтобы равные углы при его основании θ были такими же, как выбранный угол. Предположим, что выбранный угол θ противоположен стороне, отмеченной буквой c . Вписанный в равнобедренный треугольник образует треугольник CAD с углом θ против стороны b и со стороной r вдоль c . Второй треугольник образован с углом θ напротив стороны а и стороной с длиной s вдоль с , как показано на рисунке. Табит ибн Курра заявил, что стороны трех треугольников связаны следующим образом:
По мере того как угол θ приближается к π /2, основание равнобедренного треугольника сужается, а длины r и s перекрываются все меньше и меньше. Когда θ = π / 2, ADB становится прямоугольным треугольником, r + s = c , и восстанавливается исходная теорема Пифагора.
Одно доказательство показывает, что треугольник ABC имеет те же углы, что и треугольник CAD , но в противоположном порядке. (Два треугольника имеют общий угол при вершине A, оба содержат угол θ и, следовательно, имеют один и тот же третий угол в соответствии с постулатом треугольника .) Следовательно, ABC подобен отражению CAD , треугольника DAC на нижней панели. Взяв отношение сторон, противоположных и примыкающих к θ,
Аналогично, для отражения другого треугольника
Очистка дробей и добавление этих двух отношений:
требуемый результат.
Теорема остается в силе, если угол тупой, поэтому длины r и s не перекрываются.
Общие треугольники с использованием параллелограммов
Обобщение для произвольных треугольников,
зеленая область = синяя область
Конструкция для доказательства обобщения параллелограмма
Теорема Паппа о площади является дальнейшим обобщением, применимым к треугольникам, которые не являются прямоугольными, с использованием параллелограммов с трех сторон вместо квадратов (конечно, квадраты — это особый случай). На верхнем рисунке показано, что для разностороннего треугольника площадь параллелограмма на большей стороне равна сумме площадей параллелограмма на двух других сторонах при условии, что параллелограмм на длинной стороне построен, как указано (размеры, отмеченные знаком стрелки совпадают и определяют стороны нижнего параллелограмма). Эта замена квадратов параллелограммами имеет явное сходство с исходной теоремой Пифагора и считалась обобщением Паппа Александрийского в 4 г. н.э.
На нижнем рисунке показаны элементы доказательства. Сосредоточьтесь на левой стороне фигуры. Левый зеленый параллелограмм имеет ту же площадь, что и левая синяя часть нижнего параллелограмма, потому что оба имеют одинаковое основание b и высоту h . Однако левый зеленый параллелограмм также имеет ту же площадь, что и левый зеленый параллелограмм на верхнем рисунке, потому что у них одинаковое основание (верхняя левая сторона треугольника) и одинаковая высота по нормали к этой стороне треугольника. Повторяя аргумент для правой стороны рисунка, нижний параллелограмм имеет ту же площадь, что и сумма двух зеленых параллелограммов.
Твердотельная геометрия
Теорема Пифагора в трех измерениях связывает диагональ AD с тремя сторонами.
Тетраэдр с прямым углом, обращенным наружу
С точки зрения стереометрии теорема Пифагора может быть применена к трем измерениям следующим образом. Рассмотрим прямоугольное тело, как показано на рисунке. Длина диагонали BD находится по теореме Пифагора как:
где эти три стороны образуют прямоугольный треугольник. Используя горизонтальную диагональ BD и вертикальное ребро AB , длина диагонали AD затем определяется вторым применением теоремы Пифагора как:
или, делая все это за один шаг:
Этот результат представляет собой трехмерное выражение величины вектора v (диагонали AD) через его ортогональные компоненты { v k } (три взаимно перпендикулярные стороны):
Эту одношаговую формулировку можно рассматривать как обобщение теоремы Пифагора на более высокие измерения. Однако на самом деле этот результат представляет собой просто повторное применение исходной теоремы Пифагора к последовательности прямоугольных треугольников в последовательности ортогональных плоскостей.
Существенным обобщением теоремы Пифагора на три измерения является теорема де Гуа , названная в честь Жана-Поля де Гуа де Мальвеса : если тетраэдр имеет прямой угол (как угол куба ), то квадрат площади грани напротив прямого угла находится сумма квадратов площадей трех других граней. Этот результат можно обобщить, как в « n — мерной теореме Пифагора»:
Позвольте быть ортогональными векторами в ℝ n . Рассмотрим n — мерный симплекс S с вершинами . (Думайте о ( n — 1)-мерном симплексе с вершинами , не включающими начало координат, как о «гипотенузе» S , а остальные ( n — 1)-мерные грани S как о его «ногах».) Тогда квадрат объем гипотенузы S равен сумме квадратов объемов n катетов.
Это утверждение иллюстрируется в трех измерениях тетраэдром на рисунке. «Гипотенуза» — это основание тетраэдра в задней части фигуры, а «ножки» — это три стороны, исходящие из вершины на переднем плане. По мере увеличения глубины основания от вершины площадь «ножек» увеличивается, а площадь основания остается неизменной. Теорема предполагает, что когда эта глубина равна значению, создающему правую вершину, применяется обобщение теоремы Пифагора. В другой редакции:
Для n -прямоугольного n -мерного симплекса квадрат ( n — 1)-содержимого грани , противоположной правой вершине, будет равен сумме квадратов ( n — 1)-содержимого остальных граней.
Внутренние пространства продукта
Векторы, участвующие в законе параллелограмма
Теорему Пифагора можно обобщить на пространства со скалярным произведением , которые являются обобщениями знакомых 2-мерных и 3-мерных евклидовых пространств . Например, функцию можно рассматривать как вектор с бесконечным числом компонентов в пространстве внутреннего произведения, как в функциональном анализе .
В пространстве внутреннего произведения понятие перпендикулярности заменяется понятием ортогональности : два вектора v и w ортогональны, если их внутренний продукт равен нулю. Внутренний продукт является обобщением скалярного произведения векторов. Скалярный продукт называется стандартным внутренним продуктом или евклидовым внутренним продуктом. Однако возможны и другие внутренние продукты.
Понятие длины заменяется понятием нормы || в || вектора v , определенного как:
В пространстве внутреннего произведения теорема Пифагора утверждает, что для любых двух ортогональных векторов v и w мы имеем
Здесь векторы v и w подобны сторонам прямоугольного треугольника с гипотенузой, заданной векторной суммой v + w . Эта форма теоремы Пифагора является следствием свойств скалярного произведения :
где внутренние произведения перекрестных членов равны нулю из-за ортогональности.
Дальнейшим обобщением теоремы Пифагора в пространстве внутреннего произведения на неортогональные векторы является закон параллелограмма :
что говорит о том, что удвоенная сумма квадратов длин сторон параллелограмма есть сумма квадратов длин диагоналей. Любая норма, удовлетворяющая этому равенству, ipso facto является нормой, соответствующей скалярному продукту.
Тождество Пифагора можно распространить на суммы более чем двух ортогональных векторов. Если v 1 , v 2 , …, v n являются попарно ортогональными векторами в пространстве со скалярным произведением, то применение теоремы Пифагора к последовательным парам этих векторов (как описано для трехмерного пространства в разделе о твердотельной геометрии ) приводит к уравнению
Множества m -мерных объектов в n -мерном пространстве
Другое обобщение теоремы Пифагора применимо к измеримым по Лебегу наборам объектов в любом количестве измерений. В частности, квадрат меры m — мерного множества объектов в одной или нескольких параллельных m — мерных плоскостях в n — мерном евклидовом пространстве равен сумме квадратов мер ортогональных проекций объекта(ов). ) на все m -мерные координатные подпространства.
С математической точки зрения:
куда:
Неевклидова геометрия
Теорема Пифагора выводится из аксиом евклидовой геометрии , и на самом деле, если бы теорема Пифагора неверна для некоторого прямоугольного треугольника, то плоскость, в которой содержится этот треугольник, не может быть евклидовой. Точнее, теорема Пифагора подразумевает и подразумевается Евклидовым (Пятым) Постулатом Параллели . Таким образом, прямоугольные треугольники в неевклидовой геометрии
не удовлетворяют теореме Пифагора. Например, в сферической геометрии все три стороны прямоугольного треугольника (скажем , a , b и c ), ограничивающие октант единичной сферы, имеют длину, равную π /2, и все его углы прямые, что нарушает пифагорейское правило. теорема, потому что
.
Здесь рассматриваются два случая неевклидовой геометрии — сферическая геометрия и гиперболическая плоская геометрия ; в каждом случае, как и в евклидовом случае для непрямоугольных треугольников, результат, заменяющий теорему Пифагора, следует из соответствующего закона косинусов.
Однако теорема Пифагора остается верной в гиперболической и эллиптической геометрии, если условие прямоугольности треугольника заменить условием, что сумма двух углов равна третьему, скажем , A + B = C. Тогда стороны связаны следующим образом: сумма площадей кругов с диаметрами a и b равна площади круга с диаметром c .
Сферическая геометрия
Для любого прямоугольного треугольника на сфере радиуса R (например, если угол γ на рисунке прямой) со сторонами a , b , c отношение между сторонами принимает вид:
Это уравнение можно вывести как частный случай сферического закона косинусов , применимого ко всем сферическим треугольникам:
Выражая ряд Маклорена для функции косинуса как асимптотическое расширение с остатком члена в большой нотации O ,
можно показать, что по мере того, как радиус R стремится к бесконечности, а аргументы a/R , b/R и c/R стремятся к нулю, сферическое отношение между сторонами прямоугольного треугольника приближается к евклидовой форме теоремы Пифагора. Подстановка асимптотического разложения для каждого из косинусов в сферическое соотношение для прямоугольного треугольника дает
Константы a 4 , b 4 и c 4 были поглощены большими остаточными членами O , поскольку они не зависят от радиуса R. Это асимптотическое соотношение можно еще больше упростить, умножив величины в квадратных скобках, сократив единицы, умножив на -2 и собрав все члены ошибки вместе:
После умножения на R 2 евклидово пифагорейское соотношение c 2 = a 2 + b 2 восстанавливается в пределе при стремлении радиуса R к бесконечности (поскольку остаточный член стремится к нулю):
Для маленьких прямоугольных треугольников ( a , b << R ) косинусы можно исключить, чтобы избежать потери значимости , что дает
Гиперболическая геометрия
В гиперболическом пространстве с равномерной кривизной −1/ R 2 для прямоугольного треугольника с катетами a , b и гипотенузой c отношение между сторонами принимает вид:
где ch — гиперболический косинус . Эта формула представляет собой особую форму гиперболического закона косинусов , применимого ко всем гиперболическим треугольникам:
где γ угол при вершине, противоположной стороне c .
Используя ряд Маклорена для гиперболического косинуса, ch x ≈ 1 + x 2 /2 , можно показать, что по мере того, как гиперболический треугольник становится очень маленьким (то есть когда a , b и c все стремятся к нулю), гиперболический треугольник соотношение для прямоугольного треугольника приближается к форме теоремы Пифагора.
Для маленьких прямоугольных треугольников ( a , b << R ) гиперболические косинусы можно исключить, чтобы избежать потери значимости , что дает
Очень маленькие треугольники
Для любой равномерной кривизны K (положительной, нулевой или отрицательной) в очень малых прямоугольных треугольниках (| K | a 2 , | K | b 2 << 1) с гипотенузой c можно показать, что
Дифференциальная геометрия
На бесконечно малом уровне в трехмерном пространстве теорема Пифагора описывает расстояние между двумя бесконечно малыми точками как:
где ds элемент расстояния и ( dx , dy , dz ) компоненты вектора, разделяющего две точки. Такое пространство называется евклидовым пространством . Однако в римановой геометрии обобщение этого выражения, полезное для общих координат (не только декартовых) и общих пространств (не только евклидовых), принимает форму:
который называется метрическим тензором . (Иногда из-за злоупотребления языком тот же термин применяется к набору коэффициентов g ij .) Это может быть функция положения и часто описывает искривленное пространство . Простым примером является евклидово (плоское) пространство, выраженное в криволинейных координатах . Например, в полярных координатах :
История
Ведутся споры о том, была ли теорема Пифагора открыта один раз или много раз во многих местах, и дата первого открытия неизвестна, как и дата первого доказательства. Историки месопотамской математики пришли к выводу, что правило Пифагора широко использовалось в древневавилонский период (20-16 века до н.э.), более чем за тысячу лет до рождения Пифагора. Историю теоремы можно разделить на четыре части: знание пифагорейских троек , знание отношений между сторонами прямоугольного треугольника, знание отношений между соседними углами и доказательства теоремы в рамках некоторой дедуктивной системы .
Написанный между 2000 и 1786 годами до нашей эры, Берлинский папирус 6619 Среднего царства Египта включает задачу, решением которой является пифагорейская тройка 6:8:10, но в задаче не упоминается треугольник. Месопотамская табличка Plimpton 322 , написанная между 1790 и 1750 годами до нашей эры во время правления царя Хаммурапи Великого, содержит много записей, тесно связанных с пифагорейскими тройками.
В Индии Баудхаяна Шульба Сутра , даты которой даются по-разному между 8-м и 5-м веками до нашей эры, содержит список пифагорейских троек и утверждение теоремы Пифагора, как в частном случае равнобедренного прямоугольного треугольника , так и в общий случай, как и Апастамба Шулба Сутра (ок. 600 г. до н.э.).
Византийский философ- неоплатоник и математик Прокл , писавший в пятом веке нашей эры, устанавливает два арифметических правила, «одно из которых приписывается Платону , другое — Пифагору», для создания особых пифагорейских троек. Правило, приписываемое Пифагору ( ок. 570 — ок. 495 до н . э. ), начинается с нечетного числа и дает тройку с катетом и гипотенузой, отличающимися на одну единицу; правило, приписываемое Платону (428/427 или 424/423 – 348/347 до н.э.), начинается с четного числа и дает тройку с катетом и гипотенузой, отличающимися на две единицы. По словам Томаса Л. Хита (1861–1940), в сохранившейся греческой литературе за пять веков после жизни Пифагора не существует конкретного приписывания этой теоремы Пифагору. Однако, когда такие авторы, как Плутарх и Цицерон , приписывали теорему Пифагору, они делали это так, что предполагалось, что это приписывание было широко известно и не вызывало сомнений. Классик Курт фон Фриц писал: «Правильно ли эта формула приписывается лично Пифагору, но можно смело предположить, что она относится к самому древнему периоду пифагорейской математики ». Около 300 г. до н.э. в « Элементах» Евклида представлено старейшее из сохранившихся аксиоматических доказательств теоремы.
С содержанием, известным гораздо раньше, но в сохранившихся текстах, датируемых примерно I веком до нашей эры, китайский текст Zhoubi Suanjing (周髀 算 经) ( «Арифметическая классика гномона и круговых путей неба» ) дает обоснование для пифагорейцев. теорема для треугольника (3, 4, 5) — в Китае она называется « теоремой Гоугу » (勾股定理). Во времена династии Хань (202 г. до н.э. — 220 г. н.э.) пифагорейские тройки появляются в «Девяти главах математического искусства » вместе с упоминанием прямоугольных треугольников. Некоторые считают, что теорема впервые возникла в Китае , где она также известна как « теорема Шан Гао » (商高定理), названная в честь астронома и математика герцога Чжоу , чьи рассуждения составили большую часть того, что было в Zhoubi Suanjing .
Смотрите также
- Сложение в квадратуре
- В Дулкарноне
- Теорема о британском флаге
- Великая теорема Ферма
- Обратная теорема Пифагора
- треугольник Кеплера
- Линейная алгебра
- Список тем треугольника
- L п пространство
- Число без гипотенузы
- Закон параллелограмма
- Личность Парсеваля
- Теорема Птолемея
- Пифагорейское ожидание
- Пифагорейская мозаика
- Рациональная тригонометрия в теореме Пифагора
- Теорема Фалеса
Примечания и ссылки
Примечания
использованная литература
Процитированные работы
- Белл, Джон Л. (1999). Искусство понятного: элементарный обзор математики в ее концептуальном развитии . Клювер. ISBN 0-7923-5972-0.
- Евклид (1956). Тринадцать книг элементов Евклида, переведенных с текста Хейберга, с введением и комментариями . Том. 1 (Книги I и II). Перевод Хита, Томаса Л. (Переиздание 2-го (1925) изд.). Дувр.Онлайн-текст на archive.org
- Хит, сэр Томас (1921). «Теорема Пифагора».» . История греческой математики (2 тома) (Dover Publications, Inc. (1981) изд.). Clarendon Press, Oxford. Стр. 144 и далее . ISBN 0-486-24073-8.
- Либескинд, Шломо (2008). Евклидова и трансформационная геометрия: дедуктивное исследование . Джонс и Бартлетт Обучение. ISBN 978-0-7637-4366-6.Этот учебник по геометрии для старшей школы охватывает многие темы этой статьи WP.
- Лумис, Элиша Скотт (1968). Пифагорейское предложение (2-е изд.). Национальный совет учителей математики. ISBN 978-0-87353-036-1.Полный текст 2-го издания 1940 г. см. у Элиши Скотт Лумис. «Утверждение Пифагора: его демонстрации проанализированы и классифицированы, а также библиография источников данных четырех видов доказательств» (PDF) . Информационный центр образовательных ресурсов . Институт педагогических наук (IES) Министерства образования США . Проверено 4 мая 2010 г. .Первоначально опубликовано в 1940 году и переиздано в 1968 году Национальным советом учителей математики, ISBN 0-87353-036-5 .
- Маор, Эли (2007). Теорема Пифагора: 4000-летняя история . Принстон, Нью-Джерси: Издательство Принстонского университета. ISBN 978-0-691-12526-8.
- Нойгебауэр, Отто (1969). Точные науки в древности . Acta Historica Scientiarum Naturalium et Medicinalium . Том. 9 (переиздание издательства Брауновского университета 1957 г., 2-е изд.). Курьер Dover Publications. стр. 1–191. ISBN 0-486-22332-9. PMID 14884919 .
- Робсон, Элеонора и Жаклин Стедалл, редакторы, Оксфордский справочник по истории математики, Оксфорд: Oxford University Press, 2009. стр. vii + 918. ISBN 978-0-19-921312-2 .
- Стиллвелл, Джон (1989). Математика и ее история . Спрингер-Верлаг. ISBN 0-387-96981-0.Также ISBN 3-540-96981-0 .
- Свец, Франк; Као, TI (1977). Был ли Пифагор китайцем?: Исследование теории прямоугольного треугольника в Древнем Китае . Издательство Пенсильванского государственного университета. ISBN 0-271-01238-2.
-
ван дер Варден, Бартель Лендерт (1983). Геометрия и алгебра в древних цивилизациях . Спрингер. ISBN 3-540-12159-5.
Пифагорейцы троят вавилонских писцов ван дер Вардена.
внешние ссылки
- Теорема Пифагора в ProofWiki
- Евклид (1997) [ок. 300 г. до н.э.]. Дэвид Э. Джойс (ред.). Элементы . Проверено 30 августа 2006 г. .В HTML с интерактивными рисунками на основе Java.
- «Теорема Пифагора» . Энциклопедия математики . Пресс СМП . 2001 [1994].
- Историческая тема: теорема Пифагора в вавилонской математике.
- Интерактивные ссылки:
- Интерактивное доказательство теоремы Пифагора на Java
- Еще одно интерактивное доказательство теоремы Пифагора на Java
- Теорема Пифагора с интерактивной анимацией
- Анимированная, неалгебраическая и настраиваемая пользователем теорема Пифагора
- Демонстрация воды по теореме Пифагора на YouTube
- Теорема Пифагора (более 70 доказательств от cut-the-knot )
- Вайсштейн, Эрик В. «Теорема Пифагора» . Мир Математики .
Теорема Пифагора: неизвестные доказательства
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Федорова Т.С. 1
1Муниципальное бюджетное общеобразовательное учреждение «Краснооктябрьская средняя общеобразовательная школа»
Тюленева И.Ю. 1
1Муниципальное бюджетное общеобразовательное учреждение «Краснооктябрьская средняя общеобразовательная школа»
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Прежде чем приступить к возведению
дворца вселенной,
сколько нужно еще добыть
материала из рудников опыта!
К. Гельвеций
Данная работа посвящена изучению различных доказательств теоремы Пифагора, неизвестных большинству школьников.
В настоящее время всеобщее признание получило то, что успех развития многих областей науки и техники зависит от развития различных направлений математики. Важным условием повышения эффективности производства является широкое внедрение математических методов в технику и народное хозяйство, что предполагает создание новых, эффективных методов качественного и количественного исследования, которые позволяют решать задачи, выдвигаемые практикой.
Впервые о теореме Пифагора я узнала на уроках геометрии. Задачи на эту тему давались мне очень легко. В самом деле, теорема Пифагора проста, но не очевидна. Теорема имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.) свидетельствует о гигантском числе ее конкретных реализаций, поэтому эта тема и стала основой для моего исследования. Благодаря такому количеству доказательств, теорема Пифагора попала в Книгу рекордов Гиннеса, как теорема с наибольшим количеством доказательств. Это говорит о неослабевающем интересе к ней со стороны широкой математической общественности.
Исходя из вышеизложенного, определена проблема исследования: существует множество доказательств теоремы Пифагора, однако они не рассматриваются в школьной программе. Разрешение этой проблемы в первую очередь ценностно для обучения математике учащихся средней школы.
Сформулированная проблема и определила выбор темы исследовательской работы – «Теорема Пифагора: неизвестные доказательства».
Объект исследования: теорема Пифагора.
Предмет исследования: неизвестные доказательства.
Цель работы: познакомиться с различными доказательствами теоремы Пифагора, освоить методы доказательства этой теоремы.
Гипотеза исследования: еслиизучить другие доказательства теоремы, которые не рассматриваются в школьной программе, мы убедимся в её совершенстве, красоте, простоте и особой значимости в математике.
Поставленная цель и выдвинутая гипотеза определили решение следующих задач исследования:
-изучить и проанализировать литературу о теореме Пифагора;
— определить особенности различных доказательств теоремы;
— выявить её место в математике, значимость для развития науки и области применения.
Для решения поставленных задач использовались следующие методы:
— анализ литературы по теме исследования;
— обобщение и систематизация сведений.
Работа состоит из введения, четырёх параграфов, заключения, списка используемой литературы. В первом параграфе речь идёт об истории теоремы Пифагора. Во втором параграфе рассказывается об особенностях теоремы Пифагора: различные формулировки теоремы; следствия из нее; теорема, обратная теореме Пифагора; обобщение теоремы. В третьем параграфе повествуется о различных доказательствах теоремы Пифагора, незнакомых многим школьникам. В четвёртом параграфе описываются области применения теоремы.
В работе использовано 7 источников. Наиболее ценными оказались книги: «История математики в школе» Глейзера Г. И., «Теорема Пифагора» Литцмана В., «Геометрические миниатюты» Скопеца З. А.
§1. История теоремы Пифагора
И нтересна история теоремы Пифагора. Хотя эта теорема и связана с именем Пифагора, она была известна задолго до него. В вавилонских текстах эта теорема встречается за 1200 лет до Пифагора, а в Египте это соотношение использовалось для построения прямого угла еще пять тысяч лет назад. Возможно, что тогда еще не знали ее доказательства, а само соотношение между гипотенузой и катетами было установлено опытным путем на основе измерений. Пифагор, по-видимому, нашел доказательство этого соотношения. Сохранилось древнее предание, что в честь своего открытия Пифагор принес в жертву богам быка, по другим свидетельствам – даже сто быков. На протяжении последующих веков были найдены различные другие доказательства теоремы Пифагора. Это говорит о неослабевающем интересе к ней со стороны широкой математической общественности. Теорема Пифагора послужила источником для множества обобщений и плодородных идей. Глубина этой древней истины, по-видимому, далеко не исчерпана.
И сторический обзор начнем с древнего Китая. Здесь особое внимание привлекает математическая книга Чу-пей. В этом сочинении так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5: «Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4». В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.
К рупнейший немецкий историк математики Кантор считает, что равенство 32 + 42 = 52 было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора «натягиватели веревок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Н есколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммураби, т. е. к 2000 г. до н. э., приводится приближенное вычисление гипотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях.
Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой – на критическом изучении греческих источников, голландский математик Ван-дер-Варден сделал следующий вывод: «Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, является не открытие математики, но ее систематизация и обоснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку».
В настоящее время известно, что эта теорема не была открыта Пифагором. Однако одни полагают, что Пифагор первым дал ее полноценное доказательство, а другие отказывают ему и в этой заслуге. Некоторые приписывают Пифагору доказательство, которое Евклид приводит в первой книге своих «Начал».
В некоторых списках «Начал» Евклида эта теорема называлась «теоремой нимфы» за сходство чертежа с пчелкой, бабочкой, что п о-гречески называлось нимфой. Но словом этим греки называли еще некоторых богинь, а также вообще молодых женщин и невест. При переводе с греческого арабский переводчик, не обратив внимания на чертеж, перевел слово «нимфа» как «невеста», а не «бабочка». Так появилось ласковое название знаменитой теоремы – «теорема невесты».
Д оказательство теоремы Пифагора учащиеся средних веков считали очень трудным и называли его Dons asinorum – ослиный мост, или elefuga – бегство «убогих», так как некоторые «убогие» ученики, не имевшие серьезной математической подготовки, бежали от геометрии. Слабые ученики, заучившие теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста. Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли ее также «ветряной мельницей», составляли стихи, вроде «Пифагоровы штаны на все стороны равны», рисовали карикатуры.
Итак, рассматриваемая нами теорема, имеет разные названия, но в памяти школьников многих поколений хранится главное ее имя – теорема Пифагора как дань памяти великого ученого, распространившего математические знания.
§2. Особенности теоремы Пифагора
Изучая теорему Пифагора, которая отражает очень интересное соотношение между сторонами прямоугольного треугольника, обратимся к различным формулировкам теоремы, следствиям из нее, а также теоремам, связанным с ней.
Формулировки теоремы.
Приведем различные формулировки теоремы Пифагора в переводе с греческого, латинского и немецкого языков.
Во времена Пифагора теорема звучала так:
«Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах».
«Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах».
У Евклида эта теорема гласит (дословный перевод):
«В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол».
Латинский перевод арабского текста Аннаирици (около 900 г. до н. э.), сделанный Герхардом Клемонским (начало 12 в.), в переводе на русский гласит:
«Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол».
В GeometriaCulmonensis (около 1400 г.) в переводе теорема читается так:
«Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу».
В первом русском переводе евклидовых «Начал», сделанном Ф. И. Петрушевским, теорема Пифагора изложена так:
«В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол».
Существует три современные формулировки теоремы Пифагора:
1. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
2. Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах.
3. Квадрат, построенный на гипотенузе прямоугольного треугольника, равносоставлен с квадратами, построенными на катетах.
2. Теорема Пифагора имеет три следствия:
1. Если к прямой из одной точки проведены перпендикуляр и наклонная, то любая наклонная больше перпендикуляра.
2. Равные наклонные имеют равные проекции.
3. Из двух наклонных больше та, у которой проекция больше.
Теорема, обратная теореме Пифагора.
Формулировка теоремы: Если квадрат длины стороны треугольника равен сумме квадратов длин двух других сторон, то такой треугольник прямоугольный.
Докажем эту теорему.
Д ано:
Доказать:.
Доказательство теоремы.
Построим прямоугольный треугольник с катетами и . Угол – прямой. ( ; ; ).
Такой треугольник существует. В этом прямоугольном треугольнике действует прямая теорема Пифагора, то есть: .
Но по условию: .
Отсюда следует, что . Значит, .
Выясняется, что треугольники равны друг другу по трем сторонам: .
Теорема доказана.
Малоизвестное обобщение теоремы Пифагора.
Теорема Пифагора – пожалуй, самая известная из математических теорем. Сколько существует оригинальных доказательств! Сколько применений она находит в технике! Сколькими благами цивилизации мы обязаны этой великой теореме! Однако, совсем недавно, я открыла для себя совершенно новую, ранее неизвестную грань этой теоремы, которая значительно расширяет область ее применения.
Новая теорема
Итак, у нас есть все, что нужно. Прямоугольные (!) пирамиды, боковые грани-катеты и секущая грань-гипотенуза. Пришло время нарисовать еще одну картинку.
Теорема Пифагора для прямоугольной пирамиды. На картинке изображена пирамида с вершиной в начале прямоугольных координат (пирамида как бы лежит на боку). Пирамида образована тремя взаимно-перпендикулярными векторами, отложенными из начала координат вдоль координатных осей. То есть каждая боковая грань пирамиды — это прямоугольный треугольник с прямым углом при начале координат. Концы векторов определяют секущую плоскость и образуют грань-основание пирамиды.
Теорема:
П усть есть прямоугольная пирамида, образованная тремя взаимно-перпендикулярными векторами , , , у которой площади граней-катетов равны – A, B, C, и площадь грани-гипотенузы – D.
Тогда D2 = A2 + B2 + C2.
Альтернативная формулировка: У четырехгранной пирамиды, у которой при одной из вершин все плоские углы прямые, сумма квадратов площадей боковых граней равна квадрату площади основания.
Разумеется, если обычная теорема Пифагора формулируется для длин сторон треугольников, то новая теорема формулируется для площадей сторон пирамиды. Доказать эту теорему в трех измерениях очень просто, если вы немного знаете векторную алгебру.
Доказательство:
Выразим площади A, B, C, D через длины векторов , , ,
A = ab, B = ac, C = bс, гдеa = , b = , c = . Площадь D представим как половину площади параллелограмма, построенного на векторах и , где = – , = – .
Как известно, векторное произведение двух векторов – это вектор, длина которого численно равна площади параллелограмма, построенного на этих векторах.
Поэтому: D =
= (ab)2 + (ac)2 + (bc)2 .
Таким образом, D2 = (ab)2 + (ac)2 + (bc)2 = A2 + B2 + C2.
Что и требовалось доказать!
§3. Неизвестные доказательства теоремы
Самое простое доказательство.
С одной стороны площадь квадрата со стороной (а + b) равна (a + b)2, что в результате использования формулы сокращенного умножения равно a2 + 2ab + b2.
С другой стороны площадь квадрата равна сумме площадей фигур, из которых он составлен (квадрата со стороной с и 4-х равных прямоугольных треугольников с катетами а и b), а именно,
c2 + 4 ab = c2 + 2ab.
Значит, a2 + 2ab + b2= c2 + 2ab, т.е. c2 = a2 + b2.
Простейшее доказательство теоремы с помощью мозаики.
П олучается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников (рис. 1), чтобы убедиться в справедливости теоремы. Например, для треугольника ABC: квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах, – по два. Теорема доказана.
Алгебраическое доказательство.
Д ано: ABC – прямоугольный треугольник,
С = 90º.
Доказать: AB2 = AC2 + BC2
Доказательство:
1) Проведем высоту CD из вершины прямого угла С.
2) По определению косинуса угла соsА = AD/AC=AC/AB, отсюда следует AB AD = AC2.
3) Аналогично соsВ = BD/BC=BC/AB, значит AB BD = BC2.
4) Сложив почленно полученные равенства, получим:
AC2 + BC2 = АВ (AD + DB).
AB2 = AC2 + BC2.
Доказательства, основанные на использовании понятия равновеликости фигур.
П ри этом можно рассмотреть доказательства, в которых квадрат, построенный на гипотенузе данного прямоугольного треугольника «складывается» из таких же фигур, что и квадраты, построенные на катетах. Можно рассматривать и такие доказательства, в которых применяется перестановка слагаемых фигур и учитывается ряд новых идей. На рис. 2 изображено два равных квадрата. Длина сторон каждого квадрата равна a + b. Каждый из квадратов разбит на части, состоящие из квадратов и прямоугольных треугольников. Ясно, что если от площади квадрата отнять учетверенную площадь прямоугольного треугольника с катетами a, b, то останутся равные площади, т. е. c2 = a2 + b2. Впрочем, древние индусы, которым принадлежит это рассуждение, обычно не записывали его, а сопровождали чертеж лишь одним словом: «Cмотри!» Вполне возможно, что такое же доказательство предложил и Пифагор.
Доказательство Евклида.
Д ано: ABC – прямоугольный треугольник
Доказать: S(ABDE) = S(ACFG) + S(BCHI).
Доказательство:
Пусть ABDE – квадрат, построенный на гипотенузе прямоугольного треугольника ABC, а ACFG и BCHI – квадраты, построенные на его катетах. Опустим из вершины C прямого угла перпендикуляр CP на гипотенузу и продолжим его до пересечения со стороной DE квадрата ABDE в точке Q; соединим точки C и E, B и G. Очевидно, что углы CAE и GAB равны A + 90°; отсюда следует, что треугольники ACE и AGB (закрашенные на рисунке) равны между собой (по двум сторонам и углу, заключённому между ними). Сравним далее треугольник ACE и прямоугольник PQEA; они имеют общее основание AE и высоту AP, опущенную на это основание, следовательно
S(PQEA) = 2 S(ACE).
Точно так же квадрат FCAG и треугольник BAG имеют общее основание GA и высоту AC; значит,
S(FCAG) = 2 S(GAB).
Отсюда и из равенства треугольников ACE и GBA вытекает равновеликость прямоугольника QPBD и квадрата CFGA; аналогично доказывается и равновеликость прямоугольника QPAE и квадрата CHIB. А отсюда, следует, что квадрат ABDE равновелик сумме квадратов ACFG и BCHI, т.е. теорема Пифагора.
Аддитивные доказательства.
Э ти доказательства основаны на разложении квадратов, построенных на катетах, на фигуры, из которых можно сложить квадрат, построенный на гипотенузе.
Доказательство Эйнштейна основано на разложении квадрата, построенного на гипотенузе, на 8 треугольников.
Здесь: ABC – прямоугольный треугольник с прямым углом C; CMN; CKMN; PO||MN; EF||MN.
Доказательство Хоукинсa.
П риведем еще одно доказательство, которое имеет вычислительный характер, однако сильно отличается от всех предыдущих. Оно опубликовано англичанином Хоукинсом в 1909 году; было ли оно известно до этого – трудно сказать. Прямоугольный треугольник ABC с прямым углом C повернем на 90° так, чтобы он занял положение A’CB’. Продолжим гипотенузу A’В’ за точку A’ до пересечения с линией АВ в точке D. Отрезок В’D будет высотой треугольника В’АВ. Рассмотрим теперь заштрихованный четырехугольник A’АВ’В. Его можно разложить на два равнобедренных треугольника САA’ и СВВ’ (или на два треугольника A’В’А и A’В’В).
S(CAA’) = b²/2, S(CBB’) = a²/2, S(A’AB’B) = (a² + b²)/2. Треугольники A’В’А и A’В’В имеют общее основание с и высоты DA и DB, поэтому: S(A’AB’B) = c DA/2 + c DB/2 = c (DA+DB)/2 = c²/2. Сравнивая два полученных выражения для площади, получим: a² + b² = c² Теорема доказана.
Доказательство Вальдхейма.
Это доказательство также имеет вычислительный характер. Можно использовать рисунки для доказательства, основанного на вычислении площадей двумя способами.
Д ля того чтобы доказать теорему пользуясь первым рисунком, достаточно только выразить площадь трапеции двумя путями.
Sтрапеции = (a + b)²/2
Sтрапеции = a²b² + c²/2
Приравнивая правые части получим:
a² + b² = c². Теорема доказана.
Доказательство, основанное на теории подобия.
В прямоугольном треугольника АВС проведем из вершины прямого угла высоту CD; тогда треугольник разобьется на два треугольника, также являющихся прямоугольными. Полученные треугольники будут подобны друг другу и исходному треугольнику. Это легко доказать, пользуясь первым признаком подобия (по двум углам). В самом деле, сразу видно что, кроме прямого угла, треугольники АВС и ACD имеют общий угол a, треугольники CBD и АВС – общий угол b. То, что малые треугольники также подобны друг другу, следует из того, что каждый из них подобен большому треугольнику. Впрочем, это можно установить и непосредственно.
Доказательство индийского математика Басхары.
И зображено на рисунке. В пояснение к нему он написал только одну строчку: «Смотри!». Ученые считают, что он выражал площадь квадрата, построенного на гипотенузе, как сумму площадей треугольников (4ab/2) и площадь квадрата (a-b)².
Следовательно:
c² = 4ab/2 + (a – b)²
c² = 2ab + a² – 2ab + b²
c² = a² + b².
Теорема доказана.
Луночки Гиппократа.
С уществует одно интересное приложение обобщения теоремы Пифагора, которое встречается во многих учебниках геометрии под названием теоремы о гиппократовых луночках.
Гиппократ Хиосский (вторая половина пятого века до н. э., Афины) занимался квадратурой луночек. Он называл луночкой часть плоскости, ограниченную двумя дугами окружностей. Наше предложение в том виде, как оно будет здесь сформулировано, не встречается у самого Гипократа, который нашел квадратуру только для некоторых луночек. Во всей общности теорему доказал араб Ибн Альхаитам:
» Если на гипотенузе прямоугольного треугольника как на диаметре описать полуокружность, лежащую с той же стороны гипотенузы, что и сам треугольник, то она пройдет через вершину прямого угла».
Эту теорему греки приписывали Фалесу Милетскому, но в действительности ее знали еще древние вавилоняне.
Для того, чтобы доказать теорему о гиппократовых луночках, докажем следующее предложение: Если на катетах и на гипотенузе прямоугольного треугольника построены какие угодно подобные между собой фигуры Fa , Fb , Fc , так, что катеты и гипотенуза являются сходственными отрезками этих фигур, то имеет место равенство: Fa+Fb =Fc.
Для доказательства воспользуемся следующей теоремой из теории подобия: площади подобных многоугольников относятся как квадраты сходственных сторон. Если через Fa , Fb , Fc обозначить площади подобных многоугольников, построенных на катетах a, b и гипотенузе с прямоугольного треугольника, то согласно вспомогательной теореме можно написать: Fa/Fb/Fc=a²/b²/c². Эта пропорция означает, что можно найти число k (коэффицент пропорциональности) такое, что Fa = ka², Fb = kb², Fc = kc². Умножив обе части равенства на k и принимая во внимание предыдущие равенства, получим: Fa + Fb = Fc. Если равенство Fa + Fb = Fc имеет место хотя бы для одной тройки подобных между собой многоугольников, построенных на катетах и на гипотенузе прямоугольного треугольника АВС так, что АС, ВС и АВ есть сходственные отрезки этих многоугольников, то ka² + kb² = kc² (где k имеет какое-то определенное значение, зависящее от выбора многоугольников, — нам совершенно не важно, какое именно). Но отсюда вытекает, что а² + b² = с², а это влечет за собой тот факт, что равенство Fa + Fb = Fc выполняется для любых построенных на сторонах прямоугольного треугольника подобных многоугольников, в частности, и для квадратов.
Векторное доказательство.
Пусть АВС – прямоугольный треугольник с прямым углом при вершине С, построенный на векторах. Тогда справедливо векторное равенство: b + c = a откуда имеем c = a – b возводя обе части в квадрат, получим c² = a² + b² – 2ab. Так как a перпендикулярно b, то ab = 0, откуда c² = a² + b² или c² = a² + b² Нами снова доказана теорема Пифагора. Если треугольник АВС – произвольный, то та же формула дает так называемую теорему косинусов, обобщающую теорему Пифагора.
Геометрическое доказательство методом Гарфилда.
Дано: ABC – прямоугольный треугольник.
Д оказать: BC2 = AB2 + AC2.
Доказательство:
1) Построим отрезок CD равный отрезку AB на продолжении катета AC прямоугольного треугольника ABC. Затем опустим перпендикуляр ED к отрезку AD, равный отрезку AC, соединим точки B и E.
2) Площадь фигуры ABED можно найти, если рассматривать её как сумму площадей трёх треугольников: S(ABED) = 2*AB*AC/2+BC2/2
3) Фигура ABED является трапецией, значит, её площадь равна: S(ABED) = (DE+AB)*AD/2.
4) Если приравнять левые части найденных выражений, то получим: AB*AC+BC2/2 = (DE+AB)(CD+AC)/2, AB*AC+BC2/2 = (AC+AB)2/2 AB*AC+BC2/2 = AC2/2 + AB2/2 + AB*AC.
Доказательства методом достроения.
С ущность этого метода состоит в том, что к квадратам, построенным на катетах, и к квадрату, построенному на гипотенузе, присоединяют равные фигуры таким образом, чтобы получились равновеликие фигуры.
На рисунке изображена обычная Пифагорова фигура – прямоугольный треугольник ABC с построенными на его сторонах квадратами. К этой фигуре присоединены треугольники 1 и 2, равные исходному прямоугольному треугольнику.
Справедливость теоремы Пифагора вытекает из равновеликости шестиугольников AEDFPB и ACBNMQ. Здесь CEP, прямая EP делит шестиугольник AEDFPB на два равновеликих четырехугольника, прямая CM делит шестиугольник ACBNMQ на два равновеликих четырехугольника; поворот плоскости на 90° вокруг центра A отображает четырехугольник AEPB на четырехугольник ACMQ.
Доказательство через подобные треугольники.
П усть ABC – прямоугольный треугольник с прямым углом C. Проведём высоту из C. Обозначим её основание через H.
Треугольник ACH подобен треугольнику ABC по двум углам.
Аналогично, треугольник CBH подобен ABC.
a/c = HB/a, b/c = AH/b, т.е. a2 = c*HB, b2 = c*AH.
Следовательно a2 + b2 = c*(HB+AH) = c2. Что и требовалось доказать.
§4. Применение теоремы Пифагора
О бласть применения теоремы достаточно обширна. Теорема Пифагора даёт возможности для вычисления длин отрезков некоторых фигур на плоскости: Диагональ d квадрата со стороной а можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а.
Таким образом, d =2a².
Теорема Пифагора используется практически везде.
Молниеотвод
И звестно, что молниеотвод защищает от молнии все предметы, расстояние которых от его основания не превышает его удвоенной высоты. Необходимо определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.
Решение:
По теореме Пифагора h2 ≥ a2 + b2, значит, h ≥ (a2 + b2)½.
Ответ: h ≥ (a2 + b2)½.
Астрономия
Н а этом рисунке показан путь светового луча только с другой точки зрения, например из космического корабля. Предположим, что корабль движется влево. Тогда две точки, между которыми движется световой луч, станут двигаться вправо с той же скоростью. Причем, в то время, пока луч пробегает свой путь, исходная точка A смещается и луч возвращается уже в новую точку C.
Окна
В зданиях готического и романского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его очень прост: Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны ширине окна (b) для наружных дуг половине ширины, (b/2) для внутренних дуг.
Остается еще полная окружность, касающаяся четырех дуг. Т. к. она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра
Мобильная связь
В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу: Какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе (например, при радиусе R = 200 км, если известно, что радиус Земли равен 6380 км).
Решение:
Пусть АВ = х, BC = R = 200 км, ОС = r = 6380 км. ОВ = ОА + АВ, следовательно: ОВ = r + х.
Используя теорему Пифагора, получим ответ 2,3 км.
Заключение
В наши дни теорема Пифагора очень важна и актуальна. И несущественно то, что она была известна за много веков до Пифагора. Важно то, что Пифагор выделил её, дополнив собственными исследованиями, повысив значимость в мире математических открытий. Важнейшей заслугой Пифагора считается систематическое введение доказательства в математику. Только с этого момента математика и начинает существовать как наука.
Теорема Пифагора – одна из главных и, можно сказать, самая главная теорема геометрии. Она позволяет значительно расширить круг задач, решаемых в курсе геометрии и с ее помощью можно вывести большинство теорем геометрии.
К сожалению, невозможно привести все или даже самые красивые доказательства теоремы, однако приведенные примеры убедительно свидетельствуют об огромном интересе, проявляемом по отношению к ней.
Рассмотрев различные типы доказательств теоремы Пифагора, мы убедились в её совершенстве, увидев её красоту, простоту и значимость.
Список используемой литературы
Литцман В. Теорема Пифагора. М., Просвещение, 1960 г.
Еленьский Щ. По следам Пифагора. М., Учпедгиз, 1961 г
Глейзера Г. И «История математики в школе»
Скопеца З. А. «Геометрические миниатюты»
О теореме Пифагора и способах ее доказательства. http://mat.1september.ru/view_article.php?ID=200102401
Малоизвестное обобщение теоремы Пифагора. https://geektimes.ru/post/297209/
Интерактивная головоломка Теорема Пифагора. http://www.etudes.ru/ru/etudes/pythagorean-theorem/
Просмотров работы: 2574




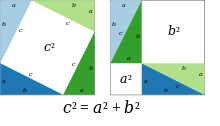











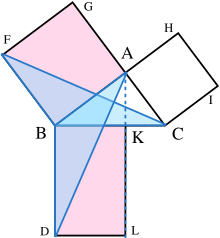



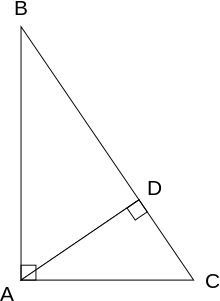








































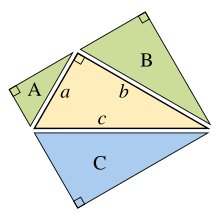
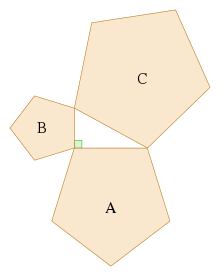







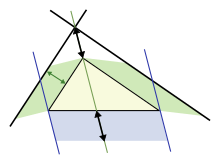





















![1 - { frac {1} {2}} left ({ frac {c} {R}} right) ^ {2} + O left ({ frac {1} {R ^ {4}} } right) = left [1 - { frac {1} {2}} left ({ frac {a} {R}} right) ^ {2} + O left ({ frac {1 } {R ^ {4}}} right) right] left [1 - { frac {1} {2}} left ({ frac {b} {R}} right) ^ {2} + O left ({ frac {1} {R ^ {4}}} right) right] { text {as}} R to infty .](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ab88b5e5c1da838bc94164e6cbdd8f54d6e8035)













