500 доказательств теоремы пифагора - Универсальный справочник

Стоило мне более суток окунуться в глубокие дебри геометрии.

Вы понимаете, что развёрнутому ответу с описанием всех возможных доказательств теоремы Пифагора можно было бы уделить отдельный ресурс и посвятить книгу. Геометрия, тригонометрия, алгебра — точные науки, как и бухгалтерия свода копейки к копейке, предполагают такое множество выведенных формул и пропорций, что применив их возрастает количество комбинаций как доказательств.

Теорема пифагора устанавливает соотношение между сторонами прямоугольного треугольника.

Сумма квадратов длин катетов равна квадрату длины гипотенузы.

Возьмём прямоугольный треугольник, в котором один угол прямой, т.е. = 90°.

Стороны, прилежащие к прямому углу, называются катетами.

Сторона, противоположная прямому углу, называется гипотенузой.

Итак, теорема Пифагора гласит: в прямоугольном треугольнике сумма квадратов длин катетов равна квадрату длины гипотенузы.

A² + B² = C²

Это утверждение одно из основных в геометрии, на котором построено множество вычислений, и на основе которого строятся даже здания и передаются данные GPS. Теорема названа в честь гревнеческого философа и математика 6 столетия до н.э. Однако свою известность теорема получила более чем через тысячу лет. Вавилонская глиняная табличка содержала в себе 15 наборов чисел, удовлетворяющих условию этой теоремы.

Некоторые историки считают, что теорема была придумана ещё древними египтянами, использующими набор цифр 3, 4, 5. Эта теория основана на том, что в распоряжении геодезистов находилась верёвка с 12 промежутками, где узлы завязаны через равные промежутки. Из этой верёвки можно было сформировать треугольник со сторонами, где количество промежутков каждой стороны удовлетворяло бы этим цифрам.

Притом такой треугольник получился бы прямоугольным.

Ранняя индийская запись, датированная между 800 и 600 годами до н.э. утверждает, что длина верёвки, растянутой по диагонали квадрата может послужить новой стороной для квадрата в два раза больше начального.

Вот где прослеживается связь с теоремой Пифагора.

Но это не доказывает, что теорема выполняется для каждого прямоугольного треугольника на плоскости. Мы должны просто поверить древним геодезистам? Нет, мы знаем множество способов доказательства данной теоремы. Сегодня теорема Пифагора насчитывает около 500 возможных, включая глупые доказательства. Из них до 350 вполне достойны гениальности.

Такие доказательства построены на математических законах и логике.

_____________________________________________________

1.Классическое доказательство теоремы Пифагора заключается в перестановочном способе.

Возьмём четыре прямоугольных треугольника с катетами a, b и гипотенузой c.

Расположим их так, чтобы гипотенузы образовали квадрат.

Ясно, что на полученной плоскости, площадь такого квадрата равна c².

Теперь сделаем из треугольников два прямоугольника, направив меньшие катеты друг к другу.

Площади получившихся квадратов равны a² и b².

И вот, в чём весь смысл. Общая площадь фигур не изменилась при одинаковых площадях треугольников.

Следовательно, пустые области на равной площади равны. То есть, c² = a² + b².

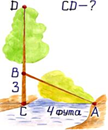
2.Ещё одно доказательство принадлежит Евклиду, на которое почти 2000 лет наткнулся и 12-летний Эйнштейн. Нам понадобится один большой треугольник и два меньших, из которых он состоит. В этом случае один большой прямоугольный треугольник делится на два других (под прямым углом).

Используется принцип, что если соответственные углы треугольника равны, то соотношение их сторон также равно.

Для трёх подобных треугольников мы можем написать соотношение их сторон.

Теперь раскроем пропорции: AC² = BC × DC и AB² = BC × BD.

Сложим одинаковые части AC² + AB² = BC × (DC + BD).

Видим, DC + BD является гипотерузой BC исходного треугольника, следовательно DC + BD = BC.

Отсюда, AC² + AB² = BC² или A² + B² = C².

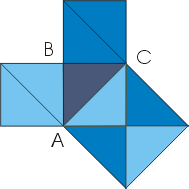
3.Более современное доказательство при тиселяции — повтора геометрического рисунка для наглядного визуального доказательства.

Пояснение.

Возьмём прямоугольный треугольник. У нас есть три ключевых элемента:

1)чёрная площадь со стороной равной длине одного катета (a).

2)серая площадь со стороной равной длине другого катета (b).

3)большая площадь синего квадрата, являющегося квадратом гипотенузы (c, d).

Чёрная и серая площади закономерно укладывются в большую площадь синего квадрата. При внимательном рассмотрении замечаем, что каждый синий квадрат вмещает ровно все составные площади для целого серого квадрата (одного катета) плюс площади для целого чёрного квадрата (другого катета). Ни больше, ни меньше.

4.Ещё один оригинальный способ доказательства, заключается в наполнении ёмкостей жидкостью. Можно попробовать соорудить вращающийся механизм, где к трём граням вала прямоугольного тетраэдра прикрепить равные по толщине квадратные ёмкости, и начать вращать вал. Жидкость начнёт вытекать из большей ёмкости в две меньшие, и ровно войдёт в обе, заполнив их.

Наша школьная учительница по математике на уроке заявила, что нашла очередной способ доказательства теоремы Пифагора. Беда в том, что дело было 20 лет назад.

Источник

Министерство образования РФ

МОУ Лицей № 1

Доклад на тему: «Пифагор и его теорема»

Ученицы группы 8 – 1, 2:

Миницкая Е. П.

Преподаватель:

Скворцова А. С.

Биография Пифагора
История теоремы
Пифагоровы числа
Доказательства теоремы (от простейших доказательств до самых сложных)

1. Биография Пифагора

Великий ученый Пифагор родился около 570
г. до н.э. на острове Самосе. Отцом Пифагора был Мнесарх, резчик по драгоценным камням. Имя же матери Пифагора неизвестно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности. Среди учителей юного Пифагора традиция называет имена старца Гермодаманта и Ферекида Сиросского (хотя и нет твердой уверенности в том, что именно Гермодамант и Ферекид были первыми учителями Пифагора). Целые дни проводил юный Пифагор у ног старца Гермодаманта, внимая мелодии кифары и гекзаметрам Гомера. Страсть к музыке и поэзии великого Гомера Пифагор сохранил на всю жизнь. И, будучи признанным мудрецом, окруженным толпой учеников, Пифагор начинал день с пения одной из песен Гомера. Ферекид же был философом и считался основателем италийской школы философии. Таким образом, если Гермодамант ввел юного Пифагора в круг муз, то Ферекид обратил его ум к логосу. Ферекид направил взор Пифагора к природе и в ней одной советовал видеть своего первого и главного учителя. Но как бы то ни было, неугомонному воображению юного Пифагора очень скоро стало тесно на маленьком Самосе, и он отправляется в Милет, где встречается с другим ученым — Фалесом. Фалес советует ему отправится за знаниями в Египет, что Пифагор и сделал.

В 548
г. до н.э. Пифагор прибыл в Навкратис — самосскую колонию, где было у кого найти кров и пищу. Изучив язык и религию египтян, он уезжает в Мемфис. Несмотря на рекомендательное письмо фараона, хитроумные жрецы не спешили раскрывать Пифагору свои тайны, предлагая ему сложные испытания. Но влекомый жаждой к знаниям, Пифагор преодолел их все, хотя по данным раскопок египетские жрецы не многому могли его научить, т.к. в то время египетская геометрия была чисто прикладной наукой (удовлетворявшей потребность того времени в счете и в измерении земельных участков). Поэтому, научившись всему, что дали ему жрецы, он, убежав от них, двинулся на родину в Элладу. Однако, проделав часть пути, Пифагор решается на сухопутное путешествие, во время которого его захватил в плен Камбиз, царь Вавилона, направлявшийся домой. Не стоит драматизировать жизнь Пифагора в Вавилоне, т.к. великий властитель Кир был терпим ко всем пленникам. Вавилонская математика была, бесспорно, более развитой (примером этому может служить позиционная система исчисления), чем египетская, и Пифагору было чему поучится. Но в 530
г. до н.э. Кир двинулся в поход против племен в Средней Азии. И, пользуясь переполохом в городе, Пифагор сбежал на родину. А на Самосе в то время царствовал тиран Поликрат. Конечно же, Пифагора не устраивала жизнь придворного полу раба, и он удалился в пещеры в окрестностях Самоса. После нескольких месяцев притязаний со стороны Поликрата, Пифагор переселяется в Кротон. В Кротоне Пифагор учредил нечто вроде религиозно — этического братства или тайного монашеского ордена («пифагорейцы»), члены которого обязывались вести так называемый пифагорейский образ жизни. Это был одновременно и религиозный союз, и политический клуб, и научное общество. Надо сказать, что некоторые из проповедуемых Пифагором принципов достойны подражания и сейчас

Прошло 20 лет. Слава о братстве разнеслась по всему миру. Однажды к Пифагору приходит Килон, человек богатый, но злой, желая спьяну вступить в братство. Получив отказ, Килон начинает борьбу с Пифагором, воспользовавшись поджогом его дома. При пожаре пифагорейцы спасли жизнь своему учителю ценой своей, после чего Пифагор затосковал и вскоре покончил жизнь самоубийством.

2. История теоремы Пифагора

Теорема Пифагора гласит: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.

Исторический обзор начнем с древнего Китая.
Здесь особое внимание привлекает математическая книга Чу — пей. В этом сочинении так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5:

«Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4»
.

В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.

Кантор
(крупнейший немецкий историк математики) считает, что равенство

3 ² + 4 ² = 5 ²

было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея).

По мнению Кантора гарпедонапты, или «натягиватели веревок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5. Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в 12 м. и привяжем к ней по цветной полоске на расстоянии 3м. от одного конца и 4 метра от другого. Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра. Гарпедонаптам можно было бы возразить, что их способ построения становиться излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент, например рисунки, изображающие столярную мастерскую.

Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммураби, т. е. к 2000 г. до н. э., приводится приближенное вычисление гипотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере, в некоторых случаях. Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой на критическом изучении греческих источников, Ван-дер-Варден
(голландский математик) сделал следующий вывод:

«Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, является не открытие математики, но ее систематизация и обоснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку».

Геометрия у индусов, как и у египтян и вавилонян, была тесно связана с культом. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 18 века до н. э.

Пифагоровы числа

В математике
пифагоровыми числами
(пифагоровой тройкой
) называется кортеж
из трёх целых чисел
удовлетворяющих соотношению Пифагора
:

x
2 + y
2 = z
2 .

Поскольку уравнение x

2
+
y

2
=
z

2
однородно
, при домножении x
, y
и z
на одно и то же число получится другая пифагорова тройка. Пифагорова тройка называется примитивной

, если она не может быть получена таким способом, то есть — взаимно простые числа
.

Треугольник
, стороны которого равны пифагоровым числам, является прямоугольным

. Кроме того, любой такой треугольник является героновым
, то есть таким, у которого все стороны и площадь
являются целочисленными. Простейший из них — египетский треугольник
со сторонами 3, 4
и 5
(3
2
+ 4
2
= 5
2
).

Пифагорова тройка задаёт точку с рациональными координатами на единичной окружности
x

2
+
y

2
= 1
.

Нетрудно видеть, что в примитивной тройке (x
, y
, z
) числа x
и y
имеют разную чётность. Любая примитивная пифагорова тройка (x
, y
, z
), где x
— нечётно, а y
— чётно, однозначно представляется в виде для некоторых натуральных взаимно простых
чисел m
> n
разной чётности
. Наоборот, любая такая пара задаёт примитивную пифагорову тройку .

Некоторые пифагоровы тройки (отсортированы по возрастанию максимального числа, выделены примитивные): (3, 4, 5),
(6, 8, 10), (5, 12, 13),
(9, 12, 15), (8, 15, 17),
(12, 16, 20), (15, 20, 25), (7, 24, 25),
(10, 24, 26), (20, 21, 29),
(18, 24, 30), (16, 30, 34), (21, 28, 35), (12, 35, 37),
(15, 36, 39), (24, 32, 40), (9, 40, 41),
(14, 48, 50), (30, 40, 50)…

Пифагоровы тройки известны очень давно. В архитектуре древнемесопотамских надгробий встречается равнобедренный треугольник, составленный из двух прямоугольных со сторонами 9, 12 и 15 локтей. Пирамиды фараона Снофру (XXVII век до н. э.) построены с использованием треугольников со сторонами 20, 21 и 29, а также 18, 24 и 30 десятков египетских локтей.

См. также в других словарях:

Пифагоровы числа
— тройки натуральных чисел таких, что треугольник, длины сторон которого пропорциональны (или равны) этим числам, является прямоугольным. По теореме, обратной теореме Пифагора (см. Пифагора теорема), для этого достаточно, чтобы они удовлетворяли… (Большая советская энциклопедия)
.

Доказательства теоремы Пифагора

На данный момент в научной литературе зафиксировано 367
доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.

Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например, с помощью дифференциальных уравнений).

Через подобные треугольники

Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся напрямую из аксиом. В частности, оно не использует понятие площади фигуры
.

П
усть ABC
есть прямоугольный треугольник с прямым углом C
. Проведём высоту из C
и обозначим её основание через H
. Треугольник ACH
подобен
треугольнику ABC
по двум углам. Аналогично, треугольник CBH
подобен ABC
. Введя обозначения

получаем

Что эквивалентно

Сложив, получаем

Доказательства методом площадей

Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.

Доказательство через равнодополняемость

Расположим четыре равных прямоугольных треугольника.
Четырёхугольник со сторонами c
является квадратом, так как сумма двух острых углов 90°, а развёрнутый угол — 180°.
Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a + b), а с другой стороны, сумме площадей четырёх треугольников и площади внутреннего квадрата.

Что и требовалось доказать.

Доказательства через равносоставленность

Элегантное доказательство при помощи перестановки. Пример одного из таких доказательств указан на чертеже справа, где квадрат, построенный на гипотенузе, перестановкой преобразуется в два квадрата, построенных на катетах.

Доказательство Евклида

Идея доказательства Евклида состоит в следующем: попробуем доказать, что половина площади квадрата, построенного на гипотенузе, равна сумме половин площадей квадратов, построенных на катетах, а тогда и площади большого и двух малых квадратов равны.

Рассмотрим чертеж справа. На нём мы построили квадраты на сторонах прямоугольного треугольника и провели из вершины прямого угла С луч s перпендикулярно гипотенузе AB, он рассекает квадрат ABIK, построенный на гипотенузе, на два прямоугольника — BHJI и HAKJ соответственно. Оказывается, что площади данных прямоугольников в точности равны площадям квадратов, построенных на соответствующих катетах.

Попытаемся доказать, что площадь квадрата DECA равна площади прямоугольника AHJK. Для этого воспользуемся вспомогательным наблюдением: площадь треугольника с той же высотой и основанием, что и данный прямоугольник, равна половине площади заданного прямоугольника. Это следствие определения площади треугольника как половины произведения основания на высоту. Из этого наблюдения вытекает, что площадь треугольника ACK равна площади треугольника AHK (не изображённого на рисунке), которая, в свою очередь, равна половине площади прямоугольника AHJK.

Докажем теперь, что площадь треугольника ACK также равна половине площади квадрата DECA. Единственное, что необходимо для этого сделать, — это доказать равенство треугольников ACK и BDA (так как площадь треугольника BDA равна половине площади квадрата по указанному выше свойству). Равенство это очевидно, треугольники равны по двум сторонам и углу между ними. Именно — AB = AK, AD = AC — равенство углов CAK и BAD легко доказать методом движения: повернём треугольник CAK на 90° против часовой стрелки, тогда очевидно, что соответствующие стороны двух рассматриваемых треугольников совпадут (ввиду того, что угол при вершине квадрата — 90°).

Рассуждение о равенстве площадей квадрата BCFG и прямоугольника BHJI совершенно аналогично.

Тем самым мы доказали, что площадь квадрата, построенного на гипотенузе, слагается из площадей квадратов, построенных на катетах. Идея данного доказательства дополнительно проиллюстрирована с помощью анимации, расположенной выше.

Доказательство
Леонардо да Винчи

Главные элементы доказательства — симметрия и движение.

Рассмотрим чертёж, как видно из симметрии, отрезок CI
рассекает квадрат ABHJ
на две одинаковые части (так как треугольники ABC
и JHI
равны по построению). Пользуясь поворотом на 90 градусов против часовой стрелки, мы усматриваем равенство заштрихованных фигур CAJI
и GDAB
. Теперь ясно, что площадь заштрихованной нами фигуры равна сумме половин площадей квадратов, построенных на катетах, и площади исходного треугольника. С другой стороны, она равна половине площади квадрата, построенного на гипотенузе, плюс площадь исходного треугольника. Последний шаг в доказательстве предоставляется Вам.

Следующее доказательство при помощи дифференциальных уравнений часто приписывают известному английскому математику Харди

, жившему в первой половине XX века.

Рассматривая чертёж, показанный на рисунке, и наблюдая изменение стороны a
, мы можем записать следующее соотношение для бесконечно малых приращений сторон с
и a
(используя подобие треугольников):

Доказательство методом бесконечно малых

Пользуясь методом разделения переменных, находим

Более общее выражение для изменения гипотенузы в случае приращений обоих катетов

Интегрируя данное уравнение и используя начальные условия, получаем

c

2
=
a

2
+
b

2
+ constant.

Таким образом, мы приходим к желаемому ответу

c

2
=
a

2
+
b

2
.

Как нетрудно видеть, квадратичная зависимость в окончательной формуле появляется благодаря линейной пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми вкладами от приращения разных катетов.

Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения (в данном случае катет b
). Тогда для константы интегрирования получим

Простейшие доказательства

Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы. Например, для треугольника ABC: квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах, — по два.

Теорема доказана.

Доказательства методом разложения

Существует целый ряд доказательств теоремы Пифагора, в которых квадраты, построенные на катетах и на гипотенузе, разрезаются так, что каждой части квадрата, построенного на гипотенузе, соответствует часть одного из квадратов, построенных на катетах. Во всех этих случаях для понимания доказательства достаточно одного взгляда на чертеж; рассуждение здесь может быть ограничено единственным словом: «Смотри!», как это делалось в сочинениях древних индусских математиков. Следует, однако, заметить, что на самом деле доказательство нельзя считать полным, пока мы не доказали равенства всех соответствующих друг другу частей. Это почти всегда довольно не трудно сделать, однако может (особенно при большом количестве частей) потребовать довольно продолжительной работы.

Доказательство Эпштейна

Начнем с доказательства Эпштейна
; его преимуществом является то, что здесь в качестве составных частей разложения фигурируют исключительно треугольники. Чтобы разобраться в чертеже, заметим, что прямая CD проведена перпендикулярно прямой EF.

Разложение на треугольники можно сделать и более наглядным, чем на рисунке.

Доказательство Нильсена

На рисунке вспомогательные линии изменены по предложению Нильсена
.

Доказательство Бетхера

На рисунке дано весьма наглядное разложение Бетхера
.

Доказательство Перигаля

В учебниках нередко встречается разложение, указанное на рисунке (так называемое «колесо с лопастями»; это доказательство нашел Перигаль
). Через центр O квадрата, построенного на большем катете, проводим прямые, параллельную и перпендикулярную гипотенузе. Соответствие частей фигуры хорошо видно из чертежа.

Доказательство Гутхейля

Изображенное на рисунке разложение принадлежит Гутхейлю; для него характерно наглядное расположение отдельных частей, что позволяет сразу увидеть, какие упрощения повлечет за собой случай равнобедренного прямоугольного треугольника.

Доказательство 9 века н.э.

Ранее были представлены только такие доказательства, в которых квадрат, построенный на гипотенузе, с одной стороны, и квадраты, построенные на катетах, с другой, складывались из равных частей. Такие доказательства называются доказательствами при помощи сложения («аддитивными доказательствами») или, чаще, доказательствами методом разложения. До сих пор мы исходили из обычного расположения квадратов, построенных на соответствующих сторонах треугольника, т. е. вне треугольника. Однако во многих случаях более выгодно другое расположение квадратов.

На рисунке квадраты, построенные на катетах, размещены ступенями один рядом с другим. Эту фигуру, которая встречается в доказательствах, датируемых не позднее, чем 9 столетием н. э., индусы называли «стулом невесты»
. Способ построения квадрата со стороной, равной гипотенузе, ясен из чертежа. Общая часть двух квадратов, построенных на катетах, и квадрата, построенного на гипотенузе, — неправильный заштрихованный пятиугольник 5. Присоединив к нему треугольники 1 и 2, получим оба квадрата, построенные на катетах; если же заменить треугольники 1 и 2 равными им треугольниками 3 и 4, то получим квадрат, построенный на гипотенузе. На рисунках ниже изображены два различных расположения близких к тому, которое дается на первом рисунке.

Доказательства методом дополнения

Доказательство первое

Наряду с доказательствами методом сложения можно привести примеры доказательств при помощи вычитания, называемых также доказательствами методом дополнения. Общая идея таких доказательств заключается в следующем.

От двух равных площадей нужно отнять равновеликие части так, чтобы в одном случае остались два квадрата, построенные на катетах, а в другом — квадрат, построенный на гипотенузе. Ведь если в равенствах

В – А = С и В 1 — А 1 = С 1

часть А
равновелика части А
1
, а часть В
равновелика В
1
, то части С
и С
1
также равновелики.

Поясним этот метод на примере. На рис. к обычной пифагоровой фигуре приставлены сверху и снизу треугольники 2 и 3, равные исходному треугольнику 1. Прямая DG обязательно пройдет через C. Заметим теперь (далее мы это докажем), что шестиугольники DABGFE и CAJKHB равновелики. Если мы от первого из них отнимем треугольники 1 и 2, то останутся квадраты, построенные на катетах, а если от второго шестиугольника отнимем равные треугольники 1 и 3, то останется квадрат, построенный на гипотенузе. Отсюда вытекает, что квадрат, построенный на гипотенузе, равновелик сумме квадратов, построенных на катетах.

Остается доказать, что наши шестиугольники равновелики. Заметим, что прямая DG делит верхний шестиугольник на равновеликие части; то же можно сказать о прямой CK и нижнем шестиугольнике. Повернем четырехугольник DABG, составляющий половину шестиугольника DABGFE, вокруг точки А по часовой стрелке на угол 90; тогда он совпадет с четырехугольником CAJK, составляющим половину шестиугольника CAJKHB. Поэтому шестиугольники DABGFE и CAJKHB равновелики.

Другое доказательство методом вычитания

Познакомимся с другим доказательством методом вычитания. Знакомый нам чертеж теоремы Пифагора заключим в прямоугольную рамку, направления сторон которой совпадают с направлениями катетов треугольника. Продолжим некоторые из отрезков фигуры так, как указано на рисунке, при этом прямоугольник распадается на несколько треугольников, прямоугольников и квадратов. Выбросим из прямоугольника сначала несколько частей так чтобы остался лишь квадрат, построенный на гипотенузе. Эти части следующие: треугольники 1, 2, 3, 4; прямоугольник 5; прямоугольник 6 и квадрат 8; прямоугольник 7 и квадрат 9;

Затем выбросим из прямоугольника части так, чтобы остались только квадраты, построенные на катетах. Этими частями будут: прямоугольники 6 и 7; прямоугольник 5; прямоугольник 1(заштрихован); прямоугольник 2(заштрихован);

Нам осталось лишь показать, что отнятые части равновелики. Это легко видеть в силу расположения фигур. Из рисунка ясно, что:

прямоугольник 5 равновелик самому себе;
четыре треугольника 1,2,3,4 равновелики двум прямоугольникам 6 и 7;
прямоугольник 6 и квадрат 8, взятые вместе, равновелики прямоугольнику 1 (заштрихован);
прямоугольник 7 вместе с квадратом 9 равновелики прямоугольнику 2(заштрихован);

Доказательство закончено.

Доказательство Евклида

Это доказательство было приведено Евклидом
в его «Началах». По свидетельству Прокла (Византия), оно придумано самим Евклидом. Доказательство Евклида приведено в предложении 47 первой книги «Начал».

На гипотенузе и катетах прямоугольного треугольника АВС строятся соответствующие квадраты, и доказывается, что прямоугольник BJLD равновелик квадрату ABFH, а прямоугольник ICEL — квадрату АСКС. Тогда сумма квадратов на катетах будет равна квадрату на гипотенузе.

В самом деле, треугольники ABD и BFC равны по двум сторонам и углу между ними:

FB = AB, BC = BD

РFBC = d + РABC = РABD

S ABD = 1/2 S BJLD,

так как у треугольника ABD и прямоугольника BJLD общее основание BD и общая высота LD. Аналогично

S FBC = 12S ABFH

(BF-общее основание, АВ – общая высота). Отсюда, учитывая, что

S ABD = S FBC ,

S BJLD = S ABFH .

Аналогично, используя равенство треугольников ВСК и АСЕ, доказывается, что

S JCEL = S ACKG .

S ABFH +S ACKG = S BJLD +S JCEL = S BCED ,

что и требовалось доказать.

Упрощенное доказательство Евклида

Как в доказательствах методом разложения, так и при доказательстве евклидового типа можно исходить из любого расположения квадратов. Иногда при этом удается достигнуть упрощений.

Пусть квадрат, построенный на одном из катетов (на рисунке это квадрат, построенный на большем катете), расположен с той же стороны катета, что и сам треугольник. Тогда продолжение противоположной катету стороны этого квадрата проходит через вершину квадрата, построенного на гипотенузе. Доказательство в этом случае оказывается совсем простым, т. к. здесь достаточно сравнить площади интересующих нас фигур с площадью одного треугольника(он заштрихован) — площадь этого треугольника равна половине площади квадрата и одновременно половине площади прямоугольника.

Доказательство Хоукинсa

Прямоугольный треугольник ABC с прямым углом C повернем на 90° так, чтобы он занял положение A»CB». Продолжим гипотенузу A»В» за точку A» до пересечения с линией АВ в точке D. Отрезок В»D будет высотой треугольника В»АВ. Рассмотрим теперь заштрихованный четырехугольник A»АВ»В. Его можно разложить на два равнобедренных треугольника САA» и СВВ» (или на два треугольника A»В»А и A»В»В).

S CAA» = b²/2

S CBB» = a²/2

S A»AB»B = (a²+b²)/2

Треугольники A»В»А и A»В»В имеют общее основание с и высоты DA и DB, поэтому:

S A»AB»B = c*DA/2+ c*DB/2 = c (DA+DB)/2 = c²/2

Сравнивая два полученных выражения для площади, получим:

a² + b² = c²

Теорема доказана.

Доказательство Вальдхейма

Это доказательство также имеет вычислительный характер. Можно использовать рисунки для доказательства основанного на вычислении площадей двумя способами.

Для того чтобы доказать теорему пользуясь первым рисунком достаточно только выразить площадь трапеции двумя путями.

Sтрапеции = (a+b) ²/2

Sтрапеции = a²b²+c²/2

Приравнивая правые части получим:

a² + b² = c²

Теорема доказана.

Знаменитую теорему Пифагора
- «в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов»
- знают все со школьной скамьи.

Ну, вы помните «Пифагоровы штаны»
, которые «во все стороны равны»
- схематический рисунок, поясняющий теорему греческого ученого.

Здесь a
и b
- катеты, а с
- гипотенуза:

Сейчас я вам расскажу об одном оригинальном доказательстве этой теоремы, о котором вы, возможно, не знали…

Но, сначала рассмотрим одну лемму
- доказанное утверждение, которое полезно не само по себе, а для доказательства других утверждений (теорем).

Возьмем прямоугольный треугольник с вершинами X
, Y
и Z
, где Z
- прямой угол и опустим перпендикуляр с прямого угла Z
на гипотенузу. Здесь W
- точка, в которой высота пересекается с гипотенузой.

Эта линия (перпендикуляр) ZW
разбивает треугольник на подобные копии самого себя.

Напомню, что подобными называются треугольники, углы у которых соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.

В нашем примере образовавшиеся треугольники XWZ
и YWZ
подобны друг другу и также подобны исходному треугольнику XYZ
.

Доказать это несложно.

Начнем с треугольника XWZ, обратите внимание, что ∠XWZ = 90, и поэтому ∠XZW = 180–90-∠X. Но 180–90-∠X - это именно то, что ∠Y, поэтому треугольник XWZ должен быть подобным (все углы равны) треугольнику XYZ. Такое же упражнение можно выполнить для треугольника YWZ.

Лемма доказана! В прямоугольном треугольнике высота (перпендикуляр), опущенная на гипотенузу, разбивает треугольник на два подобных, которые в свою очередь подобны исходному треугольнику.

Но, вернемся к нашим «Пифагоровым штанам»…

Опустим перпендикуляр на гипотенузу c
. В результате у нас образовались два прямогульных треугольника внутри нашего прямоугольного треугольника. Обозначим эти треугольники (на картинке вверху зеленым цветом) буквами A
и B
, а исходный треугольник - буквой С
.

Разумеется, площадь треугольника С
равна сумме площадей треугольников A
и B
.

Т.е. А
+ B
= С

Теперь разобьем фигуру вверху («Пифагоровы штаны») на три фигурки-домика:

Как мы уже знаем из леммы, треугольники A
, B
и C
подобны друг другу, поэтому и образовавшиеся фигурки-домики также подобны и являются масштабированными версиями друг друга.

Это означает, что соотношение площадей A
и a²
, - это то же самое, что отношение площадей B
и b²,
а также C
и c²
.

Таким образом, мы имеем A / a² = B / b² = C / c²
.

Обозначим это соотношение площадей треугольника и квадрата в фигуре-домике буквой k
.

Т.е. k
- это некий коэффициент, связывающий площадь треугольника (крыши домика) с площадью квадрата под ним:
k = A / a² = B / b² = C / c²

Из этого следует, что площади треугольников можно выразить через площади квадратов под ними таким образом:
A = ka²
, B = kb²
, и C = kc²

Но, мы помним, что A+B = C
, а значит, ka² + kb² = kc²

Или a² + b² = c²

А это и есть доказательство теоремы Пифагора
!

О теореме Пифагора и способах ее
доказательства

Г. Глейзер,
академик РАО, Москва

О теореме
Пифагора и способах ее доказательства

Статья опубликована при поддержке компании «Мастер перевода». Хотите качественный и быстрый перевод? Обратитесь в бюро нотариальных переводов «Мастер перевода». Качество услуг гарантировано постоянными клиентами бюро, среди которых множество именитых российских компаний. Посетите официальный сайт компании www.masterperevoda.ru и ознакомьтесь подробнее с предоставляемыми им услугами.

Площадь квадрата,
построенного на гипотенузе прямоугольного
треугольника, равна сумме площадей квадратов,
построенных на его катетах…

Это одна из самых известных
геометрических теорем древности, называемая
теоремой Пифагора. Ее и сейчас знают практически
все, кто когда-либо изучал планиметрию. Мне
кажется, что если мы хотим дать знать внеземным
цивилизациям о существовании разумной жизни на
Земле, то следует посылать в космос изображение
Пифагоровой фигуры. Думаю, что если эту
информацию смогут принять мыслящие существа, то
они без сложной дешифровки сигнала поймут, что на
Земле существует достаточно развитая
цивилизация.

Знаменитый греческий философ
и математик Пифагор Самосский, именем которого
названа теорема, жил около 2,5 тысяч лет тому
назад. Дошедшие до нас биографические сведения о
Пифагоре отрывочны и далеко не достоверны. С его
именем связано много легенд. Достоверно
известно, что Пифагор много путешествовал по
странам Востока, посещал Египет и Вавилон. В
одной из греческих колоний Южной Италии им была
основана знаменитая «Пифагорова школа»,
сыгравшая важную роль в научной и политической
жизни древней Греции. Именно Пифагору
приписывают доказательство известной
геометрической теоремы. На основе преданий,
распространенных известными математиками
(Прокл, Плутарх и др.), длительное время считали,
что до Пифагора эта теорема не была известна,
отсюда и название – теорема Пифагора.

Не подлежит, однако, сомнению,
что эту теорему знали за много лет до Пифагора.
Так, за 1500 лет до Пифагора древние египтяне знали
о том, что треугольник со сторонами 3, 4 и 5
является прямоугольным, и пользовались этим
свойством (т. е. теоремой, обратной теореме
Пифагора) для построения прямых углов при
планировке земельных участков и сооружений
зданий. Да и поныне сельские строители и
плотники, закладывая фундамент избы, изготовляя
ее детали, вычерчивают этот треугольник, чтобы
получить прямой угол. Это же самое проделывалось
тысячи лет назад при строительстве великолепных
храмов в Египте, Вавилоне, Китае, вероятно, и в
Мексике. В самом древнем дошедшем до нас
китайском математико-астрономическом сочинении
«Чжоу-би», написанном примерно за 600 лет до
Пифагора, среди других предложений, относящихся
к прямоугольному треугольнику, содержится и
теорема Пифагора. Еще раньше эта теорема была
известна индусам. Таким образом, Пифагор не
открыл это свойство прямоугольного
треугольника, он, вероятно, первым сумел его
обобщить и доказать, перевести тем самым из
области практики в область науки. Мы не знаем, как
он это сделал. Некоторыми историками математики
предполагается, что все же доказательство
Пифагора было не принципиальным, а лишь
подтверждением, проверкой этого свойства на ряде
частных видов треугольников, начиная с
равнобедренного прямоугольного треугольника,
для которого оно очевидно следует из рис. 1.

С глубокой древности математики
находят все новые и новые доказательства теоремы
Пифагора, все новые и новые замыслы ее
доказательств. Таких доказательств – более или
менее строгих, более или менее наглядных –
известно более полутора сотен, но стремление к
преумножению их числа сохранилось. Думаю, что
самостоятельное «открытие» доказательств
теоремы Пифагора будет полезно и современным
школьникам.

Рассмотрим некоторые примеры
доказательств, которые могут подсказать
направления таких поисков.

Доказательства, основанные
на использовании понятия равновеликости фигур.

На рис. 2 изображено два равных
квадрата. Длина сторон каждого квадрата равна a +
b. Каждый из квадратов разбит на части, состоящие
из квадратов и прямоугольных треугольников.
Ясно, что если от площади квадрата отнять
учетверенную площадь прямоугольного
треугольника с катетами a, b, то останутся равные
площади, т. е. c 2 = a 2 + b 2 . Впрочем,
древние индусы, которым принадлежит это
рассуждение, обычно не записывали его, а
сопровождали чертеж лишь одним словом: «смотри!»
Вполне возможно, что такое же доказательство
предложил и Пифагор.

Аддитивные доказательства.

Эти доказательства основаны
на разложении квадратов, построенных на катетах,
на фигуры, из которых можно сложить квадрат,
построенный на гипотенузе.

Здесь: ABC – прямоугольный
треугольник с прямым углом C; C
О
MN; CK
^
MN; PO||MN; EF||MN.

Самостоятельно докажите
попарное равенство треугольников, полученных
при разбиении квадратов, построенных на катетах
и гипотенузе.

На рис. 4 приведено
доказательство теоремы Пифагора с помощью
разбиения ан-Найризия – средневекового
багдадского комментатора «Начал» Евклида. В этом
разбиении квадрат, построенный на гипотенузе,
разбит на 3 треугольника и 2 четырехугольника.
Здесь: ABC – прямоугольный треугольник с прямым
углом C; DE = BF.

Докажите теорему с помощью
этого разбиения.

На основе доказательства
ан-Найризия выполнено и другое разложение
квадратов на попарно равные фигуры (рис. 5, здесь
ABC – прямоугольный треугольник с прямым углом C).

Еще одно доказательство
методом разложения квадратов на равные части,
называемое «колесом с лопастями», приведено на
рис. 6. Здесь: ABC– прямоугольный треугольник с
прямым углом C; O – центр квадрата, построенного
на большом катете; пунктирные прямые, проходящие
через точку O, перпендикулярны или параллельны
гипотенузе.

Это разложение квадратов
интересно тем, что его попарно равные
четырехугольники могут быть отображены друг на
друга параллельным переносом. Может быть
предложено много и других доказательств теоремы
Пифагора с помощью разложения квадратов на
фигуры.

Доказательства методом
достроения.

Сущность этого метода состоит
в том, что к квадратам, построенным на катетах, и к
квадрату, построенному на гипотенузе,
присоединяют равные фигуры таким образом, чтобы
получились равновеликие фигуры.

Справедливость теоремы
Пифагора вытекает из равновеликости
шестиугольников AEDFPB и ACBNMQ. Здесь C
О
EP, прямая EP делит
шестиугольник AEDFPB на два равновеликих
четырехугольника, прямая CM делит шестиугольник
ACBNMQ на два равновеликих четырехугольника;
поворот плоскости на 90° вокруг центра A
отображает четырехугольник AEPB на
четырехугольник ACMQ.

Теперь докажем, что фигуры,
вычитаемые в первом случае, равновелики фигурам,
вычитаемым во втором случае.

KLOA = ACPF = ACED = a 2 ;

LGBO = CBMP = CBNQ = b 2 ;

AKGB = AKLO + LGBO = c 2 ;

отсюда c 2 = a 2
+ b 2 .

OCLP = ACLF = ACED = b 2 ;

CBML = CBNQ = a 2 ;

OBMP = ABMF = c 2 ;

OBMP = OCLP + CBML;

отсюда

c 2 = a 2 + b 2 .

Рис. 11 иллюстрирует еще одно
более оригинальное доказательство, предложенное
Гофманом.
Здесь: треугольник ABC с прямым углом C; отрезок BF
перпендикулярен CB и равен ему, отрезок BE
перпендикулярен AB и равен ему, отрезок AD
перпендикулярен AC и равен ему; точки F, C, D
принадлежат одной прямой; четырехугольники ADFB и
ACBE равновелики, так как ABF=ECB; треугольники ADF и ACE
равновелики; отнимем от обоих равновеликих
четырехугольников общий для них треугольник ABC,
получим

Алгебраический метод
доказательства.

На рис. 13 ABC – прямоугольный, C –
прямой угол, CM
^
AB, b 1 – проекция катета b на
гипотенузу, a 1 – проекция катета a на
гипотенузу, h – высота треугольника, проведенная
к гипотенузе.

Из того, что
D
ABC
подобен
D
ACM следует

b 2 = cb 1 ; (1)

из того, что
D
ABC подобен
D
BCM следует

a 2 = ca 1 . (2)

Складывая почленно равенства
(1) и (2), получим a 2 + b 2 = cb 1 + ca 1
= c(b 1 + a 1) = c 2 .

Если Пифагор действительно
предложил такое доказательство, то он был знаком
и с целым рядом важных геометрических теорем,
которые современные историки математики обычно
приписывают Евклиду.

откуда следует, что c 2 =a 2 +b 2 .

во втором

Приравнивая эти выражения,
получаем теорему Пифагора.

Существует много
доказательств теоремы Пифагора, проведенных
как каждым из описанных методов, так и с помощью
сочетания различных методов. Завершая обзор
примеров различных доказательств, приведем еще
рисунки, иллюстрирующие восемь способов, на
которые имеются ссылки в «Началах» Евклида
(рис. 16 – 23). На этих рисунках Пифагорова фигура
изображена сплошной линией, а дополнительные
построения – пунктирной.

1. Ван-дер-Варден Б.Л.
Пробуждающаяся наука. Математика Древнего
Египта, Вавилона и Греции. М., 1959.
2. Глейзер Г.И. История математики в школе. М., 1982.
3. Еленьский Щ. По следам Пифагора. М., 1961.
4. Литцман В. Теорема Пифагора. М., 1960.
5. Скопец З.А. Геометрические миниатюры. М., 1990.

Потенциал к творчеству обычно приписывают гуманитарным дисциплинам, естественно научным оставляя анализ, практический подход и сухой язык формул и цифр. Математику к гуманитарным предметам никак не отнесешь. Но без творчеств в «царице всех наук» далеко не уедешь – об этом людям известно с давних пор. Со времен Пифагора, например.

Школьные учебники, к сожалению, обычно не объясняют, что в математике важно не только зубрить теоремы, аксиомы и формулы. Важно понимать и чувствовать ее фундаментальные принципы. И при этом попробовать освободить свой ум от штампов и азбучных истин – только в таких условиях рождаются все великие открытия.

К таким открытиям можно отнести и то, которое сегодня мы знаем как теорему Пифагора. С его помощью мы попробуем показать, что математика не только может, но и должна быть увлекательной. И что это приключение подходит не только ботаникам в толстых очках, а всем, кто крепок умом и силен духом.

Из истории вопроса

Строго говоря, хоть теорема и называется «теоремой Пифагора», сам Пифагор ее не открывал. Прямоугольный треугольник и его особенные свойства изучались задолго до него. Есть две полярных точки зрения на этот вопрос. По одной версии Пифагор первым нашел полноценное доказательство теоремы. По другой доказательство не принадлежит авторству Пифагора.

Сегодня уже не проверишь, кто прав, а кто заблуждается. Известно лишь, что доказательства Пифагора, если оно когда-либо существовало, не сохранилось. Впрочем, высказываются предположения, что знаменитое доказательство из «Начал» Евклида может принадлежать как раз Пифагору, и Евклид его только зафиксировал.

Также сегодня известно, что задачи о прямоугольном треугольнике встречаются в египетских источниках времен фараона Аменемхета I, на вавилонских глиняных табличках периода правления царя Хаммурапи, в древнеиндийском трактате «Сульва сутра» и древнекитайском сочинении «Чжоу-би суань цзинь».

Как видите, теорема Пифагора занимала умы математиков с древнейших времен. Подтверждением служит и около 367 разнообразных доказательств, существующих сегодня. В этом с ней не может тягаться ни одна другая теорема. Среди знаменитых авторов доказательств можно вспомнить Леонардо да Винчи и двадцатого президента США Джеймса Гарфилда. Все это говорит о чрезвычайной важности этой теоремы для математики: из нее выводится или так или иначе с нею связано большинство теорем геометрии.

Доказательства теоремы Пифагора

В школьных учебниках в основном приводят алгебраические доказательства. Но суть теоремы в геометрии, так что давайте рассмотрим в первую очередь те доказателства знаменитой теоремы, которые опираются на эту науку.

Доказательство 1

Для самого простого доказательства теоремы Пифагора для прямоугольного треугольника нужно задать идеальные условия: пусть треугольник будет не только прямоугольным, но и равнобедренным. Есть основания полагать, что именно такой треугольник первоначально рассматривали математики древности.

Утверждение «квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах»
можно проиллюстрировать следующим чертежом:

Посмотрите на равнобедренный прямоугольный треугольник ABC: На гипотенузе АС можно построить квадрат, состоящий из четырех треугольников, равных исходному АВС. А на катетах АВ и ВС построено по квадрату, каждый из которых содержит по два аналогичных треугольника.

Кстати, этот чертеж лег в основу многочисленных анекдотов и карикатур, посвященных теореме Пифагора. Самый знаменитый, пожалуй, это «Пифагоровы штаны во все стороны равны»
:

Доказательство 2

Этот метод сочетает в себе алгебру и геометрию и может рассматриваться как вариант древнеиндийского доказательства математика Бхаскари.

Постройте прямоугольный треугольник со сторонами a, b и c
(рис.1). Затем постройте два квадрата со сторонами, равными сумме длин двух катетов, – (a+b)
. В каждом из квадратов выполните построения, как на рисунках 2 и 3.

В первом квадрате постройте четыре таких же треугольника, как на рисунке 1. В результате получаться два квадрата: один со стороной a, второй со стороной b
.

Во втором квадрате четыре построенных аналогичных треугольника образуют квадрат со стороной, равной гипотенузе c
.

Сумма площадей построенных квадратов на рис.2 равна площади построенного нами квадрата со стороной с на рис.3. Это легко проверить, высчитав площади квадратов на рис. 2 по формуле. А площадь вписанного квадрата на рисунке 3. путем вычитания площадей четырех равных между собой вписанных в квадрат прямоугольных треугольников из площади большого квадрата со стороной (a+b)
.

Записав все это, имеем: a 2 +b 2 =(a+b) 2 – 2ab
. Раскройте скобки, проведите все необходимые алгебраические вычисления и получите, что a 2 +b 2 = a 2 +b 2
. При этом площадь вписанного на рис.3. квадрата можно вычислить и по традиционной формуле S=c 2
. Т.е. a 2 +b 2 =c 2
– вы доказали теорему Пифагора.

Доказательство 3

Само же древнеиндийское доказательство описано в XII веке в трактате «Венец знания» («Сиддханта широмани») и в качестве главного аргумента автор использует призыв, обращенный к математическим талантам и наблюдательности учеников и последователей: «Смотри!».

Но мы разберем это доказательство более подробно:

Внутри квадрата постройте четыре прямоугольных треугольника так, как это обозначено на чертеже. Сторону большого квадрата, она же гипотенуза, обозначим с
. Катеты треугольника назовем а
и b
. В соответствии с чертежом сторона внутреннего квадрата это (a-b)
.

Используйте формулу площади квадрата S=c 2
, чтобы вычислить площадь внешнего квадрата. И одновременно высчитайте ту же величину, сложив площадь внутреннего квадрата и площади всех четырех прямоугольных треугольников: (a-b) 2 2+4*12*a*b
.

Вы можете использовать оба варианта вычисления площади квадрата, чтобы убедиться: они дадут одинаковый результат. И это дает вам право записать, что c 2 =(a-b) 2 +4*12*a*b
. В результате решения вы получите формулу теоремы Пифагора c 2 =a 2 +b 2
. Теорема доказана.

Доказательство 4

Это любопытное древнекитайское доказательство получило название «Стул невесты» — из-за похожей на стул фигуры, которая получается в результате всех построений:

В нем используется чертеж, который мы уже видели на рис.3 во втором доказательстве. А внутренний квадрат со стороной с построен так же, как в древнеиндийском доказательстве, приведенном выше.

Если мысленно отрезать от чертежа на рис.1 два зеленых прямоугольных треугольника, перенести их к противоположным сторонам квадрата со стороной с и гипотенузами приложить к гипотенузам сиреневых треугольников, получится фигура под названием «стул невесты» (рис.2). Для наглядности можно то же самое проделать с бумажными квадратами и треугольниками. Вы убедитесь, что «стул невесты» образуют два квадрата: маленькие со стороной b
и большой со стороной a
.

Эти построения позволили древнекитайским математикам и нам вслед за ними прийти к выводу, что c 2 =a 2 +b 2
.

Доказательство 5

Это еще один способ найти решение для теоремы Пифагора, опираясь на геометрию. Называется он «Метод Гарфилда».

Постройте прямоугольный треугольник АВС
. Нам надо доказать, что ВС 2 =АС 2 +АВ 2
.

Для этого продолжите катет АС
и постройте отрезок CD
, который равен катету АВ
. Опустите перпендикулярный AD
отрезок ED
. Отрезки ED
и АС
равны. Соедините точки Е
и В
, а также Е
и С
и получите чертеж, как на рисунке ниже:

Чтобы доказать терему, мы вновь прибегаем к уже опробованному нами способу: найдем площадь получившейся фигуры двумя способами и приравняем выражения друг к другу.

Найти площадь многоугольника ABED
можно, сложив площади трех треугольников, которые ее образуют. Причем один из них, ЕСВ
, является не только прямоугольным, но и равнобедренным. Не забываем также, что АВ=CD
, АС=ED
и ВС=СЕ
– это позволит нам упростить запись и не перегружать ее. Итак, S ABED =2*1/2(AB*AC)+1/2ВС 2
.

При этом очевидно, что ABED
– это трапеция. Поэтому вычисляем ее площадь по формуле: S ABED =(DE+AB)*1/2AD
. Для наших вычислений удобней и наглядней представить отрезок AD
как сумму отрезков АС
и CD
.

Запишем оба способа вычислить площадь фигуры, поставив между ними знак равенства: AB*AC+1/2BC 2 =(DE+AB)*1/2(AC+CD)
. Используем уже известное нам и описанное выше равенство отрезков, чтобы упростить правую часть записи: AB*AC+1/2BC 2 =1/2(АВ+АС) 2
. А теперь раскроем скобки и преобразуем равенство: AB*AC+1/2BC 2 =1/2АС 2 +2*1/2(АВ*АС)+1/2АВ 2
. Закончив все преобразования, получим именно то, что нам и надо: ВС 2 =АС 2 +АВ 2
. Мы доказали теорему.

Конечно, этот список доказательств далеко не полный. Теорему Пифагора также можно доказать с помощью векторов, комплексных чисел, дифференциальный уравнений, стереометрии и т.п. И даже физики: если, например, в аналогичные представленным на чертежах квадратные и треугольные объемы залить жидкость. Переливая жидкость, можно доказать равенство площадей и саму теорему в итоге.

Пару слов о Пифагоровых тройках

Этот вопрос мало или вообще не изучается в школьной программе. А между тем он является очень интересным и имеет большое значение в геометрии. Пифагоровы тройки применяются для решения многих математических задач. Представление о них может пригодиться вам в дальнейшем образовании.

Так что же такое Пифагоровы тройки? Так называют натуральные числа, собранные по трое, сумма квадратов двух из которых равна третьему числу в квадрате.

Пифагоровы тройки могут быть:

примитивными (все три числа – взаимно простые);
не примитивными (если каждое число тройки умножить на одно и то же число, получится новая тройка, которая не является примитивной).

Еще до нашей эры древних египтян завораживала мания чисел Пифагоровых троек: в задачах они рассматривали прямоугольный треугольник со сторонами 3,4 и 5 единиц. К слову, любой треугольник, стороны которого равны числам из пифагоровой тройки, по умолчанию является прямоугольным.

Примеры Пифагоровых троек: (3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (10, 30, 34), (21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (27, 36, 45), (14, 48, 50), (30, 40, 50) и т.д.

Практическое применение теоремы

Теорема Пифагора находит применение не только в математике, но и в архитектуре и строительстве, астрономии и даже литературе.

Сначала про строительство: теорема Пифагора находит в нем широкое применение в задачах разного уровня сложности. Например, посмотрите на окно в романском стиле:

Обозначим ширину окна как b
, тогда радиус большой полуокружности можно обозначить как R
и выразить через b: R=b/2
. Радиус меньших полуокружностей также выразим через b: r=b/4
. В этой задаче нас интересует радиус внутренней окружности окна (назовем его p
).

Теорема Пифагора как раз и пригодиться, чтобы вычислить р
. Для этого используем прямоугольный треугольник, который на рисунке обозначен пунктиром. Гипотенуза треугольника состоит из двух радиусов: b/4+p
. Один катет представляет собой радиус b/4
, другой b/2-p
. Используя теорему Пифагора, запишем: (b/4+p) 2 =(b/4) 2 +(b/2-p) 2
. Далее раскроем скобки и получим b 2 /16+ bp/2+p 2 =b 2 /16+b 2 /4-bp+p 2
. Преобразуем это выражение в bp/2=b 2 /4-bp
. А затем разделим все члены на b
, приведем подобные, чтобы получить 3/2*p=b/4
. И в итоге найдем, что p=b/6
– что нам и требовалось.

С помощью теоремы можно вычислить длину стропила для двускатной крыши. Определить, какой высоты вышка мобильной связи нужна, чтобы сигнал достигал определенного населенного пункта. И даже устойчиво установить новогоднюю елку на городской площади. Как видите, эта теорема живет не только на страницах учебников, но и часто бывает полезна в реальной жизни.

Что касается литературы, то теорема Пифагора вдохновляла писателей со времен античности и продолжает это делать в наше время. Например, немецкого писателя девятнадцатого века Адельберта фон Шамиссо она вдохновила на написание сонета:

Свет истины рассеется не скоро,
Но, воссияв, рассеется навряд
И, как тысячелетия назад,
Не вызовет сомнения и спора.

Мудрейшие, когда коснется взора
Свет истины, богов благодарят;
И сто быков, заколоты, лежат –
Ответный дар счастливца Пифагора.

С тех пор быки отчаянно ревут:
Навеки всполошило бычье племя
Событие, помянутое тут.

Им кажется: вот-вот настанет время,
И сызнова их в жертву принесут
Какой-нибудь великой теореме.

(перевод Виктора Топорова)

А в двадцатом веке советский писатель Евгений Велтистов в книге «Приключения Электроника» доказательствам теоремы Пифагора отвел целую главу. И еще полглавы рассказу о двухмерном мире, какой мог бы существовать, если бы теорема Пифагора стала основополагающим законом и даже религией для отдельно взятого мира. Жить в нем было бы гораздо проще, но и гораздо скучнее: например, там никто не понимает значения слов «круглый» и «пушистый».

А еще в книге «Приключения Электроника» автор устами учителя математики Таратара говорит: «Главное в математике – движение мысли, новые идеи». Именно этот творческий полет мысли порождает теорема Пифагора – не зря у нее столько разнообразных доказательств. Она помогает выйти за границы привычного, и на знакомые вещи посмотреть по-новому.

Заключение

Эта статья создана, чтобы вы могли заглянуть за пределы школьной программы по математике и узнать не только те доказательства теоремы Пифагора, которые приведены в учебниках «Геометрия 7-9» (Л.С. Атанасян, В.Н. Руденко) и «Геометрия 7-11» (А.В. Погорелов), но и другие любопытные способы доказать знаменитую теорему. А также увидеть примеры, как теорема Пифагора может применяться в обычной жизни.

Во-первых, эта информация позволит вам претендовать на более высокие баллы на уроках математики – сведения по предмету из дополнительных источников всегда высоко оцениваются.

Во-вторых, нам хотелось помочь вам прочувствовать, насколько математика интересная наука. Убедиться на конкретных примерах, что в ней всегда есть место творчеству. Мы надеемся, что теорема Пифагора и эта статья вдохновят вас на самостоятельные поиски и волнующие открытия в математике и других науках.

Расскажите нам в комментариях, показались ли вам приведенные в статье доказательства интересными. Пригодились ли вам эти сведения в учебе. Напишите нам, что думаете о теореме Пифагора и этой статье – нам будет приятно обсудить все это с вами.

blog.сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Теорема Пифагора всем известна со школьной поры. Выдающийся математик доказал великую гипотезу, которой в настоящее время пользуются многие люди. Звучит правило так: квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов катетов. За многие десятилетия ни один математик не сумел переспорить данное правило. Ведь Пифагор долго шел к своей цели, чтобы в результате чертежи имели место в повседневной жизни.

Небольшой стих к данной теореме, который придумали вскоре после доказательства, напрямую доказывает свойства гипотезы: «Пифагоровы штаны во все стороны равны»
. Это двустрочье отложилось в памяти у многих людей – по сей день стихотворение вспоминают при вычислениях.
Данная теорема получила название «Пифагоровы штаны» вследствие того, что при черчении по середине получался прямоугольный треугольник, по бокам которого располагались квадраты
. С виду данное черчение напоминало штаны – отсюда и название гипотезы.
Пифагор гордился разработанной теоремой, ведь данная гипотеза отличается от ею подобных максимальным количеством доказательств
. Важно: уравнение было занесено в книгу рекордов Гиннесса вследствие 370 правдивых доказательств.
Гипотезу доказывало огромное количество математиков и профессоров из разных стран многими способами
. Английский математик Джонс вскоре оглашения гипотезы доказал ее при помощи дифференциального уравнения.
В настоящее время никому неизвестно доказательство теоремы самим Пифагором
. Факты о доказательствах математика сегодня не известны никому. Считается, что доказательство чертежей Евклидом — это и есть доказательство Пифагора. Однако некоторые ученые спорят с этим утверждением: многие считают, что Евклид самостоятельно доказал теорему, без помощи создателя гипотезы.
Нынешние ученые обнаружили, что великий математик был не первым, кто открыл данную гипотезу
. Уравнение было известно еще задолго до открытия Пифагором. Данный математик сумел лишь воссоединить гипотезу.
Пифагор не давал уравнению название «Теорема Пифагора»
. Это название закрепилось после «громкого двустрочья». Математик лишь хотел, чтобы его старания и открытия узнал весь мир и пользовался ими.
Мориц Кантор — великий крупнейший математик нашел и разглядел на древнем папирусе записи с чертежами
. Вскоре после этого Кантор понял, что данная теорема была известна египтянам еще 2300 лет до нашей эры. Только тогда ею никто не воспользовался и не стал пытаться доказать.
Нынешние ученые считают, что гипотеза была известна еще в 8 веке до нашей эры
. Индийские ученые того времени обнаружили приблизительное вычисление гипотенузы треугольника, наделенного прямыми углами. Правда в то время никто не смог доказать наверняка уравнение по приблизительным вычислениям.
Великий математик Бартель Ван дер Варден после доказательства гипотезы заключил важный вывод
: «Заслуга греческого математика считается не открытием направления и геометрии, а лишь ее обоснованием. В руках Пифагора были вычислительные формулы, которые основывались на предположениях, неточных вычислениях и смутных представлениях. Однако выдающемуся ученому удалось превратить из в точную науку».
Известный стихотворец сказал, что в день открытия своего чертежа он воздвиг быкам славную жертву
. Именно после открытия гипотезы пошли слухи, что жертвоприношение ста быков «пошло странствовать по страницам книг и изданий». Остряки по сей день шутят, что с тех пор все быки боятся нового открытия.
Доказательство того, что не Пифагор придумал стихотворение про штаны, дабы доказать выдвинутые им чертежи: во времена жизни великого математика штанов еще не было
. Они были придуманы через несколько десятилетий.
Размышления Пифагора о собственном правиле: секрет сущего на земле кроется в цифрах
. Ведь математик, опираясь на собственную гипотезу, изучил свойства чисел, выявил четность и нечетность, создал пропорции.

Источник

Различные способы доказательства теоремы Пифагора

учащаяся 9 «А» класса

МОУ СОШ №8

Научный руководитель:

учитель математики,

МОУ СОШ №8

ст. Новорождественской

Краснодарского края.

Ст. Новорождественская

АННОТАЦИЯ.

Теорема Пифагора по праву считается самой важной в курсе геометрии и заслуживает пристального внимания. Она является основой решения множества геометрических задач, базой для изучения теоретического и практического курса геометрии в дальнейшем. Теорема окружена богатейшим историческим материалом, связанным с её появлением и способами доказательства. Изучение истории развития геометрии прививает любовь к данному предмету, способствует развитию познавательного интереса, общей культуры и творчества, а так же развивает навыки научно-исследовательской работы .

В результате поисковой деятельности была достигнута цель работы, заключающаяся в пополнении и обобщении знаний по доказательству теоремы Пифагора. Удалось найти и рассмотреть различные способы доказательства и углубить знания по теме, выйдя за страницы школьного учебника.

Собранный материал ещё больше убеждает в том, что теорема Пифагора является великой теоремой геометрии, имеет огромное теоретическое и практическое значение.

Введение. Историческая справка 5 Основная часть 8

3. Заключение 19

4. Используемая литература 20
1. ВВЕДЕНИЕ. ИСТОРИЧЕСКАЯ СПРАВКА.

Суть истины вся в том, что нам она — навечно,

Когда хоть раз в прозрении ее увидим свет,

И теорема Пифагора через столько лет

Для нас, как для него, бесспорна, безупречна.

На радостях богам был Пифагором дан обет:

За то, что мудрости коснулся бесконечной,

Он сто быков заклал, благодаря предвечных;

Моленья и хвалы вознес он жертве вслед.

С тех пор быки, когда учуят, тужась,

Что к новой истине людей опять подводит след,

Ревут остервенело, так что слушать мочи нет,

Такой в них Пифагор вселил навеки ужас.

Быкам, бессильным новой правде противостоять,

Что остается? — Лишь глаза закрыв, реветь, дрожать.

Неизвестно, каким способом доказывал Пифагор свою теорему. Несомненно лишь то, что он открыл ее под сильным влиянием египетской науки. Частный случай теоремы Пифагора — свойства треугольника со сторонами 3, 4 и 5 — был известен строителям пирамид задолго до рождения Пифагора, сам же он более 20 лет обучался у египетских жрецов. Сохранилась легенда, которая гласит, что, доказав свою знаменитую теорему, Пифагор принес богам в жертву быка, а по другим источникам, даже 100 быков. Это, однако, противоречит сведениям о моральных и религиозных воззрениях Пифагора. В литературных источниках можно прочитать, что он «запрещал даже убивать животных, а тем более ими кормиться, ибо животные имеют душу, как и мы». Пифагор питался только медом, хлебом, овощами и изредка рыбой. В связи со всем этим более правдоподобной можно считать следующую запись: «…и даже когда он открыл, что в прямоугольном треугольнике гипотенуза имеет соответствие с катетами, он принес в жертву быка, сделанного из пшеничного теста».

Популярность теоремы Пифагора столь велика, что ее доказательства встречаются даже в художественной литературе , например, в рассказе известного английского писателя Хаксли «Юный Архимед». Такое же Доказательство, но для частного случая равнобедренного прямоугольного треугольника приводится в диалоге Платона «Менон».

Сказка «Дом».

«Далеко-далеко, куда не летают даже самолеты, находится страна Геометрия. В этой необычной стране был один удивительный город — город Теорем. Однажды в этот город пришла красивая девочка по имени Гипотенуза. Она попробовала снять комнату, но куда бы она ни обращалась, ей всюду отказывали. Наконец она подошла к покосившемуся домику и постучала. Ей открыл мужчина, назвавший себя Прямым Углом, и он предложил Гипотенузе поселиться у него. Гипотенуза осталась в доме, в котором жили Прямой Угол и два его маленьких сына по имени Катеты. С тех пор жизнь в доме Прямого Угла пошла по-новому. На окошке гипотенуза посадила цветы, а в палисаднике развела красные розы. Дом принял форму прямоугольного треугольника. Обоим катетам Гипотенуза очень понравилась и они попросили ее остаться навсегда в их доме. Ло вечерам эта дружная семья собирается за семейным столом. Иногда Прямой Угол играет со своими детишками в прятки. Чаще всего искать приходится ему, а Гипотенуза прячется так искусно, что найти ее бывает очень трудно. Однажды во время игры Прямой Угол подметил интересное свойство: если ему удается найти катеты, то отыскать Гипотенузу не составляет труда. Так Прямой Угол пользуется этой закономерностью, надо сказать, очень успешно. На свойстве этого прямоугольного треугольника и основана теорема Пифагора.»

(Из книги А. Окунева «Спасибо за урок, дети»).

Шутливая формулировка теоремы:

Если дан нам треугольник

И притом с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдем:

Катеты в квадрат возводим,

Сумму степеней находим –

И таким простым путем

К результату мы придем.

Изучая алгебру и начала анализа и геометрию в 10 классе , я убедилась в том, что кроме рассмотренного в 8 классе способа доказательства теоремы Пифагора существуют и другие способы доказательства. Представляю их на ваше обозрение.
2. ОСНОВНАЯ ЧАСТЬ.

Теорема. В прямоугольном треугольнике квадрат

гипотенузы равен сумме квадратов катетов.

1 СПОСОБ.

Пользуясь свойствами площадей многоугольников, установим замечательное соотношение между гипотенузой и катетами прямоугольного треугольника.

Доказательство.

а, в
и гипотенузой с
(рис.1, а).

Докажем, что с²=а²+в²
.

Доказательство.

Достроим треугольник до квадрата со стороной а + в
так, как показано на рис. 1, б. Площадь S этого квадрата равна (а + в)² . С другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна ½ав
, и квадрата со стороной с,
поэтому S= 4 *
½ав + с
² =
2ав + с
².

Таким образом,

(а + в
)² = 2ав + с
²,

с²=а²+в²
.

Теорема доказана.
2 СПОСОБ.

После изучения темы «Подобные треугольники» я выяснила, что можно применить подобие треугольников к доказательству теоремы Пифагора. А именно, я воспользовалась утверждением о том, что катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключённого между катетом и высотой, проведённой из вершины прямого угла.

Рассмотрим прямоугольный треугольник с прямым углом С, СD– высота (рис. 2). Докажем, что АС
² +СВ
² = АВ
²
.

Доказательство.

На основании утверждения о катете прямоугольного треугольника:

АС = , СВ = .

Возведем в квадрат и сложим полученные равенства:

АС² = АВ * АD, СВ² = АВ * DВ;

АС² + СВ² = АВ * (АD + DВ), где АD+DB=AB, тогда

АС² + СВ² = АВ * АВ,

АС² + СВ² = АВ².

Доказательство закончено.
3 СПОСОБ.

К доказательству теоремы Пифагора можно применить определение косинуса острого угла прямоугольного треугольника. Рассмотрим рис. 3.

Доказательство:

Пусть АВС – данный прямоугольный треугольник с прямым углом С. Проведем высоту СD из вершины прямого угла С.

По определению косинуса угла:

cos А = АD/АС = АС/АВ. Отсюда АВ * АD = АС²

Аналогично,

cos В = ВD/ВС = ВС/АВ.

Отсюда АВ * ВD = ВС² .

Складывая полученные равенства почленно и замечая, что АD + DВ = АВ, получим:

АС
² + ВС
²
= АВ (АD + DВ) = АВ
²

Доказательство закончено.
4 СПОСОБ.

Изучив тему «Соотношения между сторонами и углами прямоугольного треугольника», я думаю, что теорему Пифагора можно доказать ещё одним способом.

Рассмотрим прямоугольный треугольник с катетами а, в
и гипотенузой с
. (рис. 4).

Докажем, что с²=а²+в².

Доказательство.

sinВ=
в/с ;
cosВ=
a/с,
то, возведя в квадрат полученные равенства, получим:

sin²В=
в²/с²; cos²В
= а²/с².

Сложив их, получим:

sin²В
+ cos²В=
в²/с²+ а²/с², где sin²В
+ cos²В=1,

1= (в²+ а²) / с², следовательно,

с²= а² + в².

Доказательство закончено.

5 СПОСОБ.

Данное доказательство основано на разрезании квадратов, построенных на катетах (рис. 5), и укладывании полученных частей на квадрате, построенном на гипотенузе.

6 СПОСОБ.

Для доказательства на катете ВС
строим BCD ABC
(рис.6). Мы знаем, что площади подобных фигур относятся как квадраты их сходственных линейных размеров:

Вычитая из первого равенства второе, получим

с2 = а2 +

b2.

Доказательство закончено.

7 СПОСОБ.

Дано
(рис. 7):

ABС,
= 90°, ВС
= а, АС=
b, АВ = с.

Доказать:
с2 = а2 +
b2
.

Доказательство.

Пусть катет b а.
Продолжим отрезок СВ
за точку В
и построим треугольник BMD
так, чтобы точки М
и А
лежали по одну сторону от прямой CD
и, кроме того, BD =
b, BDM
= 90°, DM
= a, тогда BMD
= ABC
по двум сторонам и углу между ними. Точки А и М
соединим отрезками AM.
Имеем MD CD
и AC CD,
значит, прямая АС
параллельна прямой MD.
Так как MD < АС,
то прямые CD
и AM
не параллельны. Следовательно, AMDC —
прямоугольная трапеция.

В прямоугольных треугольниках ABC и BMD
1 + 2 = 90° и 3 + 4 = 90°, но так как = =, то 3 + 2 = 90°; тогда АВМ
=180° — 90° = 90°. Оказалось, что трапеция AMDC
разбита на три неперекрывающихся прямоугольных треугольника, тогда по аксиомам площадей

(a+b)(a+b)

Разделив все члены неравенства на , получим

а
b + с2 + а
b = (а +
b)
, 2
ab
+ с2 = а2
+ 2а
b
+ b2,

с2 = а2 +

b2.

Доказательство закончено.

8 СПОСОБ.

Данный способ основывается на гипотенузе и катетах прямоугольного треугольника ABC.
Он строит соответствующие квадраты и доказывает, что квадрат, построенный на гипотенузе, равновелик сумме квадратов, построенных на катетах (рис. 8).

Доказательство.

1) DBC
= FBA
= 90°;

DBC + ABC
= FBA + ABC,
значит, FBC = DBA.

Таким образом, FBC
=ABD
(по двум сторонам и углу между ними).

2) ,
где AL DE, так как BD — общее основание, DL —
общая высота.

3) , так как FB –снование, АВ
— общая высота.

5) Аналогично можно доказать, что

6) Складывая почленно, получаем:

, ВС2

= АВ2 + АС2

.
Доказательство закончено.

9 СПОСОБ.

Доказательство.

1) Пусть ABDE
— квадрат (рис. 9), сторона которого равна гипотенузе прямоугольного треугольника ABC (АВ
= с, ВС = а, АС =
b).

2) Пусть DK BC
и DK = ВС,
так как 1 + 2 = 90° (как острые углы прямоугольного треугольника), 3 + 2 = 90° (как угол квадрата), АВ
= BD
(стороны квадрата).

Значит, ABC
= BDK
(по гипотенузе и острому углу).

3)Пусть EL
DK, AM EL.
Можно легко доказать, что ABC = BDK =DEL = ЕАМ (с катетами а
и b).
Тогда КС
= СМ
= ML
= LK
= а —
b.

4) SKB = 4S + SKLMC
= 2ab
+ (a — b),
с
2
= 2ab + a2 — 2ab + b2,
c2 = a2 + b2
.

Доказательство закончено.

10 СПОСОБ.

Доказательство может быть проведено на фигуре, в шутке называемой «Пифагоровы штаны» (рис. 10). Идея его состоит в преобразовании квадратов, построенных на катетах, в равновеликие треугольники, составляющие вместе квадрат гипотенузы.

ABC
сдвигаем, как показано стрелкой, и он занимает положение KDN.
Оставшаяся часть фигуры AKDCB
равновелика площади квадрата AKDC –
это параллелограмм AKNB.

Сделана модель параллелограмма AKNB
. Параллелограмм перекладываем так, как зарисовано в содержании работы. Чтобы показать преобразование параллелограмма в равновеликий треугольник, на глазах учащихся отрезаем на модели треугольник и перекладываем его вниз. Таким образом, площадь квадрата AKDC
получилась равна площади прямоугольника. Аналогично преобразуем площадь квадрата в площадь прямоугольника.

Произведем преобразование для квадрата, построенного на катете а
(рис. 11,а):

а) квадрат преобразуется в равновеликий параллелограмм (рис. 11,6):

б) параллелограмм поворачивается на четверть оборота (рис. 12):

в) параллелограмм преобразуется в равновеликий прямоугольник (рис. 13): 11 СПОСОБ.

Доказательство:

PCL –
прямая (Рис. 14);

KLOA
= ACPF
= ACED
= а2;

LGBO
= СВМР =
CBNQ
= b2;

AKGB
= AKLO +
LGBO
= с2;

с2 = а2 +

b2.

Доказательство окончено.

12 СПОСОБ.

Рис. 15 иллюстрирует еще одно оригинальное доказательство теоремы Пифагора.

Здесь: треугольник ABC с прямым углом С; отрезок BF
перпендикулярен СВ
и равен ему, отрезок BE
перпендикулярен АВ
и равен ему, отрезок AD
перпендикулярен АС
и равен ему; точки F, С,
D
принадлежат одной прямой; четырехугольники ADFB
и АСВЕ
равновелики, так как ABF = ЕСВ;
треугольники ADF
и АСЕ
равновелики; отнимем от обоих равновеликих четырехугольников общий для них треугольник ABC,
получим

, с2 = а2 +

b2.

Доказательство закончено.

13 СПОСОБ.

Площадь данного прямоугольного треугольника, с одной стороны, равна ,
с другой, ,

3. ЗАКЛЮЧЕНИЕ.

В результате поисковой деятельности была достигнута цель работы, заключающаяся в пополнении и обобщении знаний по доказательству теоремы Пифагора. Удалось найти и рассмотреть различные способы её доказательства и углубить знания по теме, выйдя за страницы школьного учебника.

Собранный мною материал ещё больше убеждает в том, что теорема Пифагора является великой теоремой геометрии, имеет огромное теоретическое и практическое значение. В завершении хотелось бы сказать: причина популярности теоремы Пифагора триедина — это красота, простота и значимость!

4. ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА.

1. Занимательная алгебра. . Москва «Наука», 1978.

2. Еженедельное учебно-методическое приложение к газете «Первое сентября», 24/2001.

3. Геометрия 7-9. и др.

4. Геометрия 7-9. и др.

Анимационное доказательство теоремы Пифагора – одна из основополагающих
теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Считается, что она доказана греческим математиком Пифагором, в честь которого она названа (есть и другие версии, в частности альтернативное мнение, что эта теорема в общем виде была сформулирована математиком-пифагорейцем Гиппасом).
Теорема гласит:

В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе равна сумме площадей квадратов, построенных на катетах.

Обозначив длину гипотенузы треугольника c,
а длины катетов как a
и b,
получим следующую формулу:

Таким образом, теорема Пифагора устанавливает соотношение, которое позволяет определить сторону прямоугольного треугольника, зная длины двух других. Теорема Пифагора является частным случаем теоремы косинусов, которая определяет соотношение между сторонами произвольного треугольника.
Также доказано обратное утверждение (называют также обратной теореме Пифагора):

Для любых трех положительных чисел a, b и c, таких что a ? + b ? = c ?, существует прямоугольный треугольник с катетами a и b и гипотенузой c.

Визуальное доказательство для треугольника (3, 4, 5) из книги «Чу Пэй» 500-200 до н.э. Историю теоремы можно разделить на четыре части: знание о Пифагоровы числа, знания об отношении сторон в прямоугольном треугольнике, знание об отношении смежных углов и доказательство теоремы.
Мегалитические сооружения около 2500 до н.э. в Египте и Северной Европе, содержат прямоугольные треугольники со сторонами из целых чисел. Бартель Леендерт ван дер Варден высказал гипотезу, что в те времена Пифагоровы числа были найдены алгебраически.
Написанный между 2000 и 1876 до н.э. папирус времен Среднего Египетского царства Berlin 6619
содержит задачу решением которой являются числа Пифагора.
Во время правления Хаммурапи Великого, вивилонська табличка Plimpton 322,
написанная между 1790 и 1750 до н.э содержит много записей тесно связанных с числами Пифагора.
В сутрах Будхаяны, которые датируются по разным версиям восьмой или второй веками до н.э. в Индии, содержит Пифагоровы числа выведены алгебраически, формулировка теоремы Пифагора и геометрическое доказательство для ривнобедренного прямоугольного треугольника.
В сутрах Апастамба (около 600 до н.э.) содержится числовое доказательство теоремы Пифагора с использованием вычисления площади. Ван дер Варден считает, что оно было основано на традициях предшественников. Согласно Альбертом Бурко, это оригинальное доказательство теоремы и он предполагает, что Пифагор посетил Араконам и скопировал его.
Пифагор, годы жизни которого обычно указывают 569 – 475 до н.э. использует алгебраические методы расчета пифагоровых чисел, согласно Проклова комментариями к Евклида. Прокл, однако, жил между 410 и 485 годами н.э. Согласно Томасом Гизом, нет никаких указаний на авторство теоремы течение пяти веков после Пифагора. Однако, когда такие авторы как Плутарх или Цицерон приписывают теорему Пифагору, они делают это так, будто авторство широко известно и несомненно.
Около 400 до н. э соответствии Прокла, Платон дал метод расчета пифагоровых чисел, сочетавший алгебру и геометрию. Около 300 до н.э., в Началах
Евклида имеем древнейшее аксиоматическое доказательство, которое сохранилось до наших дней.
Написанные где-то между 500 до н.э. и 200 до н.э., китайский математическая книга «Чу Пэй» (? ? ? ?), дает визуальное доказательство теоремы Пифагора, которая в Китае называется теорема гугу (????), для треугольника со сторонами (3, 4, 5). Во время правления династии Хань, с 202 до н.э. до 220 н.э. Пифагоровы числа появляются в книге «Девять разделов математического искусства» вместе с упоминанием о прямоугольные треугольники.
Впервые зафиксировано использование теоремы в Китае, где она известна как теорема гугу (????) и в Индии, где она известна как теорема Баскара.
Многие дискутируется была теорема Пифагора открыта один раз или многократно. Бойер (1991) считает, что знания обнаружены в Шульба Сутра могут быть месопотамского происхождения.
Алгебраическое доказательство
Квадраты образуются из четырех прямоугольных треугольников. Известно более ста доказательств теоремы Пифагора. Здесь представлены доказательства основан на теореме существования площади фигуры:

Разместим четыре одинаковые прямоугольные треугольники так, как это изображено на рисунке.
Четырехугольник со сторонами c
является квадратом, так как сумма двух острых углов , А развернутый угол – .
Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной «a + b», а с другой – сумме площадей четырех треугольников и внутреннего квадрата.

Что и необходимо доказать.
По сходству треугольников
Использование подобных треугольников. Пусть ABC
– прямоугольный треугольник, в котором угол C
прямой, как показано на рисунке. Проведем высоту с точки C,
и назовем H
точку пересечения со стороной AB.
Образован треугольник ACH
подобен треугольника ABC,
поскольку они оба прямоугольные (по определению высоты), и у них общий угол A,
очевидно третий угол будет в этих треугольников также одинаков. Аналогично миркуюючы, треугольник CBH
также подобен треугольника ABC.
С подобия треугольников: Если

Это можно записать в виде

Если добавить эти две равенства, получим

HB + c times AH = c times (HB + AH) = c ^ 2, ! Src = «http://upload.wikimedia.org/math/7/0/9/70922f59b11b561621c245e11be0b61b.png» />

Другими словами, теорема Пифагора:

Доказательство Евклида
Доказательство Евклида в евклидовых «Началах», теорема Пифагора доказана методом параллелограммов. Пусть A, B, C
вершины прямоугольного треугольника, с прямым углом A.
Опустим перпендикуляр из точки A
на сторону противоположную гипотенузы в квадрате построенном на гипотенузе. Линия делит квадрат на два прямоугольника, каждый из которых имеет такую же площадь, что и квадраты построены на катетах. Главная идея при доказательстве состоит в том, что верхние квадраты превращаются в параллелограммы такой же площади, а потом возвращаются и превращаются в прямоугольники в нижнем квадрате и снова при неизменной площади.

Проведем отрезки CF
и AD,
получим треугольники BCF
и BDA.

Углы CAB
и BAG
– прямые; соответственно точки C, A
и G
– коллинеарны. Так же B, A
и H.

Углы CBD
и FBA
– оба прямые, тогда угол ABD
равен углу FBC,
поскольку оба являются суммой прямого угла и угла ABC.

Треугольник ABD
и FBC
уровне по двум сторонам и углу между ними.
Поскольку точки A, K
и L
– коллинеарны, площадь прямоугольника BDLK равна двум площадям треугольника ABD (BDLK
= BAGF
= AB 2)

Аналогично миркуюючы получим CKLE
= ACIH
= AC 2

С одной стороны площадь CBDE
равна сумме площадей прямоугольников BDLK
и CKLE,
а с другой стороны площадь квадрата BC 2,
или AB 2
+ AC 2
= BC 2.

Используя дифференциалы
Использование дифференциалов. Теореме Пифагора можно прийти, если изучать как прирост стороны влияет на ведичину гипотенузы как показано на рисунке справа и применить небольшое вычисления.
В результате прироста стороны a,
из подобных треугольников для бесконечно малых приращений

Интегрируя получим

Если a
= 0 тогда c
= b,
так что «константа» – b 2.
Тогда

Как можно увидеть, квадраты получен благодаря пропорции между приращениями и сторонами, тогда как сумма является результатом независимого вклада приростов сторон, не очевидно из геометрических доказательств. В этих уравнениях da
и dc
– соответственно бесконечно малые приращения сторон a
и c.
Но вместо них мы используем? a
и? c,
тогда предел отношения, если они стремятся к нулю равна da
/ dc,
производная, и также равен c
/ a,
отношению длин сторон треугольников, в результате получаем дифференциальное уравнение.
В случае ортогональной системы векторов имеет место равенство, которую также называют теоремой Пифагора:

Если – Это проекции вектора на координатные оси, то эта формула совпадает с расстоянием Евклида и означает, что длина вектора равна корню квадратному суммы квадратов его компонентов.
Аналог этого равенства в случае бесконечной системы векторов называется равенства Парсеваля.

В одном можно быть уверенным на все сто процентов, что на вопрос, чему равен квадрат гипотенузы, любой взрослый человек смело ответит: «Сумме квадратов катетов». Эта теорема прочно засела в сознании каждого образованного человека, но достаточно лишь попросить кого-либо ее доказать, и тут могут возникнуть сложности. Поэтому давайте вспомним и рассмотрим разные способы доказательства теоремы Пифагора.

Краткий обзор биографии

Теорема Пифагора знакома практически каждому, но почему-то биография человека, который произвел ее на свет, не так популярна. Это поправимо. Поэтому прежде чем изучить разные способы доказательства теоремы Пифагора, нужно кратко познакомиться с его личностью.

Пифагор — философ, математик, мыслитель родом из Сегодня очень сложно отличить его биографию от легенд, которые сложились в память об этом великом человеке. Но как следует из трудов его последователей, Пифагор Самосский родился на острове Самос. Его отец был обычный камнерез, а вот мать происходила из знатного рода.

Судя по легенде, появление на свет Пифагора предсказала женщина по имени Пифия, в чью честь и назвали мальчика. По ее предсказанию рожденный мальчик должен был принести много пользы и добра человечеству. Что вообще-то он и сделал.

Рождение теоремы

В юности Пифагор переехал с в Египет, чтобы встретиться там с известными египетскими мудрецами. После встречи с ними он был допущен к обучению, где и познал все великие достижения египетской философии, математики и медицины.

Вероятно, именно в Египте Пифагор вдохновился величеством и красотой пирамид и создал свою великую теорию. Это может шокировать читателей, но современные историки считают, что Пифагор не доказывал свою теорию. А лишь передал свое знание последователям, которые позже и завершили все необходимые математические вычисления.

Как бы там ни было, сегодня известна не одна методика доказательства данной теоремы, а сразу несколько. Сегодня остается лишь гадать, как именно древние греки производили свои вычисления, поэтому здесь рассмотрим разные способы доказательства теоремы Пифагора.

Теорема Пифагора

Прежде чем начинать какие-либо вычисления, нужно выяснить, какую теорию предстоит доказать. Теорема Пифагора звучит так: «В треугольнике, у которого один из углов равен 90 о, сумма квадратов катетов равна квадрату гипотенузы».

Всего существует 15 разных способов доказательства теоремы Пифагора. Это достаточно большая цифра, поэтому уделим внимание самым популярным из них.

Способ первый

Сначала обозначим, что нам дано. Эти данные будут распространяться и на другие способы доказательств теоремы Пифагора, поэтому стоит сразу запомнить все имеющееся обозначения.

Допустим, дан прямоугольный треугольник, с катетами а, в и гипотенузой, равной с. Первый способ доказательства основывается на том, что из прямоугольного треугольника нужно дорисовать квадрат.

Чтобы это сделать, нужно к катету длиной а дорисовать отрезок равный катету в, и наоборот. Так должно получиться две равные стороны квадрата. Остается только нарисовать две параллельные прямые, и квадрат готов.

Внутри получившейся фигуры нужно начертить еще один квадрат со стороной равной гипотенузе исходного треугольника. Для этого от вершин ас и св нужно нарисовать два параллельных отрезка равных с. Таким образом, получиться три стороны квадрата, одна из которых и есть гипотенуза исходного прямоугольного треугольники. Остается лишь дочертить четвертый отрезок.

На основании получившегося рисунка можно сделать вывод, что площадь внешнего квадрата равна (а+в) 2 . Если заглянуть внутрь фигуры, можно увидеть, что помимо внутреннего квадрата в ней имеется четыре прямоугольных треугольника. Площадь каждого равна 0,5ав.

Поэтому площадь равна: 4*0,5ав+с 2 =2ав+с 2

Отсюда (а+в) 2 =2ав+с 2

И, следовательно, с 2 =а 2 +в 2

Теорема доказана.

Способ два: подобные треугольники

Данная формула доказательства теоремы Пифагора была выведена на основании утверждения из раздела геометрии о подобных треугольниках. Оно гласит, что катет прямоугольного треугольника — среднее пропорциональное для его гипотенузы и отрезка гипотенузы, исходящего из вершины угла 90 о.

Исходные данные остаются те же, поэтому начнем сразу с доказательства. Проведем перпендикулярный стороне АВ отрезок СД. Основываясь на вышеописанном утверждении катеты треугольников равны:

АС=√АВ*АД, СВ=√АВ*ДВ.

Чтобы ответить на вопрос, как доказать теорему Пифагора, доказательство нужно проложить возведением в квадрат обоих неравенств.

АС 2 =АВ*АД и СВ 2 =АВ*ДВ

Теперь нужно сложить получившиеся неравенства.

АС 2 + СВ 2 =АВ*(АД*ДВ), где АД+ДВ=АВ

Получается, что:

АС 2 + СВ 2 =АВ*АВ

И, следовательно:

АС 2 + СВ 2 =АВ 2

Доказательство теоремы Пифагора и различные способы ее решения нуждаются в разностороннем подходе к данной задаче. Однако этот вариант является одним из простейших.

Еще одна методика расчетов

Описание разных способов доказательства теоремы Пифагора могут ни о чем не сказать, до тех самых пор пока самостоятельно не приступишь к практике. Многие методики предусматривают не только математические расчеты, но и построение из исходного треугольника новых фигур.

В данном случае необходимо от катета ВС достроить еще один прямоугольный треугольник ВСД. Таким образом, теперь имеется два треугольника с общим катетом ВС.

Зная, что площади подобных фигур имеют соотношение как квадраты их сходных линейных размеров, то:

S авс * с 2 — S авд *в 2 =S авд *а 2 — S всд *а 2

S авс *(с 2 -в 2)=а 2 *(S авд -S всд)

с 2 -в 2 =а 2

с 2 =а 2 +в 2

Поскольку из разных способов доказательств теоремы Пифагора для 8 класса этот вариант едва ли подойдет, можно воспользоваться следующей методикой.

Самый простой способ доказать теорему Пифагора. Отзывы

Как полагают историки, этот способ был впервые использован для доказательства теоремы еще в древней Греции. Он является самым простым, так как не требует абсолютно никаких расчетов. Если правильно начертить рисунок, то доказательство утверждения, что а 2 +в 2 =с 2 , будет видно наглядно.

Условия для данного способа будет немного отличаться от предыдущего. Чтобы доказать теорему, предположим, что прямоугольный треугольник АВС — равнобедренный.

Гипотенузу АС принимаем за сторону квадрата и дочерчиваем три его стороны. Кроме этого необходимо провести две диагональные прямые в получившемся квадрате. Таким образом, чтобы внутри него получилось четыре равнобедренных треугольника.

К катетам АВ и СВ так же нужно дочертить по квадрату и провести по одной диагональной прямой в каждом из них. Первую прямую чертим из вершины А, вторую — из С.

Теперь нужно внимательно всмотреться в получившийся рисунок. Поскольку на гипотенузе АС лежит четыре треугольника, равные исходному, а на катетах по два, это говорит о правдивости данной теоремы.

Кстати, благодаря данной методике доказательства теоремы Пифагора и появилась на свет знаменитая фраза: «Пифагоровы штаны во все стороны равны».

Доказательство Дж. Гарфилда

Джеймс Гарфилд — двадцатый президент Соединенных Штатов Америки. Кроме того, что он оставил свой след в истории как правитель США, он был еще и одаренным самоучкой.

В начале своей карьеры он был обычным преподавателем в народной школе, но вскоре стал директором одного из высших учебных заведений. Стремление к саморазвитию и позволило ему предложить новую теорию доказательства теоремы Пифагора. Теорема и пример ее решения выглядит следующим образом.

Сначала нужно начертить на листе бумаги два прямоугольных треугольника таким образом, чтобы катет одного из них был продолжением второго. Вершины этих треугольников нужно соединить, чтобы в конечном итоге получилась трапеция.

Как известно, площадь трапеции равна произведению полусуммы ее оснований на высоту.

S=а+в/2 * (а+в)

Если рассмотреть получившуюся трапецию, как фигуру, состоящую из трех треугольников, то ее площадь можно найти так:

S=ав/2 *2 + с 2 /2

Теперь необходимо уравнять два исходных выражения

2ав/2 + с/2=(а+в) 2 /2

с 2 =а 2 +в 2

О теореме Пифагора и способах ее доказательства можно написать не один том учебного пособия. Но есть ли в нем смысл, когда эти знания нельзя применить на практике?

Практическое применение теоремы Пифагора

К сожалению, в современных школьных программах предусмотрено использование данной теоремы только в геометрических задачах. Выпускники скоро покинут школьные стены, так и не узнав, а как они могут применить свои знания и умения на практике.

На самом же деле использовать теорему Пифагора в своей повседневной жизни может каждый. Причем не только в профессиональной деятельности, но и в обычных домашних делах. Рассмотрим несколько случаев, когда теорема Пифагора и способы ее доказательства могут оказаться крайне необходимыми.

Связь теоремы и астрономии

Казалось бы, как могут быть связаны звезды и треугольники на бумаге. На самом же деле астрономия — это научная сфера, в которой широко используется теорема Пифагора.

Например, рассмотрим движение светового луча в космосе. Известно, что свет движется в обе стороны с одинаковой скоростью. Траекторию АВ, которой движется луч света назовем l
.
А половину времени, которое необходимо свету, чтобы попасть из точки А в точку Б, назовем
t
. И скорость луча —
c
.
Получается, что: c*t=l

Если посмотреть на этот самый луч из другой плоскости, например, из космического лайнера, который движется со скоростью v, то при таком наблюдении тел их скорость изменится. При этом даже неподвижные элементы станут двигаться со скоростью v в обратном направлении.

Допустим, комический лайнер плывет вправо. Тогда точки А и В, между которыми мечется луч, станут двигаться влево. Причем, когда луч движется от точки А в точку В, точка А успевает переместиться и, соответственно, свет уже прибудет в новую точку С. Чтобы найти половину расстояния, на которое сместилась точка А, нужно скорость лайнера умножить на половину времени путешествия луча (t»).

А чтобы найти, какое расстояние за это время смог пройти луч света, нужно обозначить половину пути новой буковой s и получить следующее выражение:

Если представить, что точки света С и В, а также космический лайнер — это вершины равнобедренного треугольника, то отрезок от точки А до лайнера разделит его на два прямоугольных треугольника. Поэтому благодаря теореме Пифагора можно найти расстояние, которое смог пройти луч света.

Этот пример, конечно, не самый удачный, так как только единицам может посчастливиться опробовать его на практике. Поэтому рассмотрим более приземленные варианты применения этой теоремы.

Радиус передачи мобильного сигнала

Современную жизнь уже невозможно представить без существования смартфонов. Но много ли было бы от них прока, если бы они не могли соединять абонентов посредством мобильной связи?!

Качество мобильной связи напрямую зависит от того, на какой высоте находиться антенна мобильного оператора. Для того чтобы вычислить, каком расстоянии от мобильной вышки телефон может принимать сигнал, можно применить теорему Пифагора.

Допустим, нужно найти приблизительную высоту стационарной вышки, чтобы она могла распространять сигнал в радиусе 200 километров.

АВ (высота вышки) = х;

ВС (радиус передачи сигнала) = 200 км;

ОС (радиус земного шара) = 6380 км;

ОВ=ОА+АВОВ=r+х

Применив теорему Пифагора, выясним, что минимальная высота вышки должна составить 2,3 километра.

Теорема Пифагора в быту

Как ни странно, теорема Пифагора может оказаться полезной даже в бытовых делах, таких как определение высоты шкафа-купе, например. На первый взгляд, нет необходимости использовать такие сложные вычисления, ведь можно просто снять мерки с помощью рулетки. Но многие удивляются, почему в процессе сборки возникают определенные проблемы, если все мерки были сняты более чем точно.

Дело в том, что шкаф-купе собирается в горизонтальном положении и только потом поднимается и устанавливается к стене. Поэтому боковина шкафа в процессе подъема конструкции должна свободно проходить и по высоте, и по диагонали помещения.

Предположим, имеется шкаф-купе глубиной 800 мм. Расстояние от пола до потолка — 2600 мм. Опытный мебельщик скажет, что высота шкафа должна быть на 126 мм меньше, чем высота помещения. Но почему именно на 126 мм? Рассмотрим на примере.

При идеальных габаритах шкафа проверим действие теоремы Пифагора:

АС=√АВ 2 +√ВС 2

АС=√2474 2 +800 2 =2600 мм — все сходится.

Допустим, высота шкафа равна не 2474 мм, а 2505 мм. Тогда:

АС=√2505 2 +√800 2 =2629 мм.

Следовательно, этот шкаф не подойдет для установки в данном помещении. Так как при поднятии его в вертикальное положение можно нанести ущерб его корпусу.

Пожалуй, рассмотрев разные способы доказательства теоремы Пифагора разными учеными, можно сделать вывод, что она более чем правдива. Теперь можно использовать полученную информацию в своей повседневной жизни и быть полностью уверенным, что все расчеты будут не только полезны, но и верны.

Тем, кто интересуется историей теоремы Пифагора, которую изучают в школьной программе, будет также любопытен такой факт, как публикация в 1940 году книги с трехсот семьюдесятью доказательствами этой, казалось бы, простой теоремы. Но она интриговала умы многих математиков и философов разных эпох. В книге рекордов Гиннеса она зафиксирована, как теорема с самым максимальным числом доказательств.

История теоремы Пифагора

Связанная с именем Пифагора, теорема была известна задолго до рождения великого философа. Так, в Египте, при строительстве сооружений, учитывалось соотношение сторон прямоугольного треугольника пять тысячелетий назад. В вавилонских текстах упоминается о все том же соотношении сторон прямоугольного треугольника за 1200 лет до рождения Пифагора.

Возникает вопрос, почему тогда гласит история — возникновение теоремы Пифагора принадлежит ему? Ответ может быть только один — он доказал соотношение сторон в треугольнике. Он сделал то, что века назад не делали те, кто просто пользовался соотношением сторон и гипотенузы, установленным опытным путем.

Из жизни Пифагора

Будущий великий ученый, математик, философ родился на острове Самосе в 570 году до нашей эры. Исторические документы сохранили сведения об отце Пифагора, который был резчиком по драгоценным камням, а вот о матери сведений нет. О родившемся мальчике говорили, что это незаурядный ребенок, проявивший с детского возраста страсть к музыке и поэзии. К учителям юного Пифагора историки относят Гермодаманта и Ферекида Сиросского. Первый ввел мальчика в мир муз, а второй, будучи философом и основателем итальянской школы философии, направил взор юноши к логосу.

В 22 года от роду (548 г. до н. э.) Пифагор отправился в Навкратис для изучения языка и религии египтян. Далее его путь лежал в Мемфис, где благодаря жрецам, пройдя через их хитроумные испытания, он постиг египетскую геометрию, которая, возможно натолкнула пытливого юношу на доказательство теоремы Пифагора. История в дальнейшем припишет теореме именно это имя.

В плену царя Вавилона

По пути домой в Элладу, Пифагор попадает в плен царя Вавилона. Но нахождение в плену принесло пользу пытливому уму начинающего математика, ему было чему поучиться. Ведь в те годы математика в Вавилоне была более развитой чем в Египте. Двенадцать лет он провел за изучением математики, геометрии и магии. И, возможно, именно вавилонская геометрия причастна к доказательству соотношения сторон треугольника и истории открытия теоремы. У Пифагора было для этого достаточно полученных знаний и времени. Но, что это произошло в Вавилоне, документального подтверждения или опровержения тому нет.

В 530 г. до н.э. Пифагор бежит из плена на родину, где живет при дворе тирана Поликрата в статусе полураба. Такая жизнь Пифагора не устраивает, и он удаляется в пещеры Самоса, а затем отправляется на юг Италии, где в то время располагалась греческая колония Кротон.

Тайный монашеский орден

На базе этой колонии Пифагор организовал тайный монашеский орден, представлявший собой религиозный союз и научное общество одновременно. Это общество имело свой устав, в котором говорилось о соблюдении особого образа жизни.

Пифагор утверждал, чтобы понять Бога, человек должен познать такие науки как алгебра и геометрия, знать астрономию и понимать музыку. Исследовательская работа сводилась к познанию мистической стороны чисел и философии. Следует отметить, что проповедованные в то время Пифагором принципы, имеют смысл в подражании и в настоящее время.

Многие из открытий, которые делали ученики Пифагора, приписывались ему. Тем не менее, если говорить кратко, история создания теоремы Пифагора древними историками и биографами того времени, связывается непосредственно с именем этого философа, мыслителя и математика.

Учение Пифагора

Возможно, на мысль о связи теоремы с именем Пифагора натолкнуло историков высказывание великого грека, что в пресловутом треугольнике с его катетами и гипотенузой зашифрованы все явления нашей жизни. А этот треугольник является «ключом» к решению всех возникающих проблем. Великий философ говорил, что следует узреть треугольник, тогда можно считать, что задача на две трети решена.

О своем учении Пифагор рассказывал только своим ученикам устно, не делая никаких записей, держа его в тайне. К великому сожалению, учение величайшего философа не сохранилось до наших дней. Что-то из него просочилось, но нельзя сказать сколько истинного, а сколько ложного в том, что стало известно. Даже с историей теоремы Пифагора не все бесспорно. Историки математики сомневаются в авторстве Пифагора, по их мнению теоремой пользовались за много веков до его рождения.

Теорема Пифагора

Может показаться странным, но исторических фактов доказательства теоремы самим Пифагором нет — ни в архивах, ни в каких-либо других источниках. В современной версии считается, что оно принадлежит не кому иному, как самому Евклиду.

Есть доказательства одного из крупнейших историков математики Морица Кантора, обнаружившего на папирусе, хранящемся в Берлинском музее, записанное египтянами примерно в 2300 году до н. э. равенство, которое гласило: 3² + 4² = 5².

Кратко из истории теоремы Пифагора

Формулировка теоремы из евклидовых «Начал», в переводе звучит также как и в современной интерпретации. Нового в ее прочтении нет: квадрат стороны противолежащей прямому углу, равен сумме квадратов сторон, прилегающих к прямому углу. О том, что теоремой пользовались древние цивилизации Индии и Китая подтверждает трактат «Чжоу — би суань цзинь». Он содержит сведения об египетском треугольнике, в котором описано соотношение сторон как 3:4:5.

Не менее интересна еще одна китайская математическая книга «Чу-пей», в которой также упоминается о пифагоровом треугольнике с пояснением и рисунками, совпадающими с чертежами индусской геометрии Басхары. О самом треугольнике в книге написано, что если прямой угол можно разложить на составные части, тогда линия, которая соединяет концы сторон, будет равна пяти, если основание равно трем, а высота равна четырем.

Индийский трактат «Сульва сутра», относящийся примерно к VII-V векам до н. э., рассказывает о построении прямого угла при помощи египетского треугольника.

Доказательство теоремы

В средние века ученики считали доказательство теоремы слишком трудным делом. Слабые ученики заучивали теоремы наизусть, без понимания смысла доказательства. В связи с этим они получили прозвище «ослы», потому что теорема Пифагора была для них непреодолимым препятствием, как для осла мост. В средние века ученики придумали шутливый стих на предмет этой теоремы.

Чтобы доказать теорему Пифагора самым легким путем, следует просто измерить его стороны, не используя в доказательстве понятие о площадях. Длина стороны, противолежащая прямому углу — это c, а прилежащие к нему a и b, в результате получаем уравнение: a 2 + b 2 = c 2 . Данное утверждение, как говорилось выше, проверяется путем измерения длин сторон прямоугольного треугольника.

Если начать доказательство теоремы с рассмотрения площади прямоугольников, построенных на сторонах треугольника, можно определить площадь всей фигуры. Она будет равна площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырех треугольников и внутреннего квадрата.

(a + b) 2 = 4 x ab/2 + c 2 ;

a 2 + 2ab + b 2 ;

c 2 = a 2 + b 2 , что и требовалось доказать.

Практическое значение теоремы Пифагора заключается в том, что с ее помощью можно найти длины отрезков, не измеряя их. При строительстве сооружений рассчитываются расстояния, размещение опор и балок, определяются центры тяжести. Применяется теорема Пифагора и во всех современных технологиях. Не забыли о теореме и при создании кино в 3D-6D-измерениях, где кроме привычных нам 3-х величин: высоты, длины, ширины — учитываются время, запах и вкус. Как связаны с теоремой вкусы и запахи — спросите вы? Все очень просто — при показе фильма нужно рассчитать, куда и какие запахи и вкусы направлять в зрительном зале.

То ли еще будет. Безграничный простор для открытия и создания новых технологий ждет пытливые умы.

ИЗМЕРЕНИЕ ПЛОЩАДЕЙ ГЕОМЕТРИЧЕСКИХ ФИГУР.

§ 58. ТЕОРЕМА ПИФАГОРА 1 .

__________
1 Пифагор — греческий учёный, живший около 2500 лет назад (564-473 гг. до нашей эры).

_________

Пусть дан прямоугольный треугольник, стороны которого а
, b
и с
(черт. 267).

Построим на его сторонах квадраты. Площади этих квадратов соответственно равны а
2 , b
2 и с
2 . Докажем, что с
2 = а
2 + b
2 .

Построим два квадрата МКОР и М»К»О»Р» (черт. 268, 269), приняв за сторону каждого из них отрезок, равный сумме катетов прямоугольного треугольника АBС.

Выполнив в этих квадратах построения, показанные на чертежах 268 и 269, мы увидим, что квадрат МКОР разбился на два квадрата с площадями а
2 и b
2 и четыре равных прямоугольных треугольника, каждый из которых равен прямоугольному треугольнику АВС. Квадрат М»К»О»Р» разбился на четырёхугольник (он на чертеже 269 заштрихован) и четыре прямоугольных треугольника, каждый из которых также равен треугольнику АBС. Заштрихованный четырёхугольник — квадрат, так как стороны его равны (каждая равна гипотенузе треугольника АBС, т. е. с
), а углы — прямые /
1 + /
2 = 90°, откуда /
3 = 90°).

Таким образом, сумма площадей квадратов, построенных на катетах (на чертеже 268 эти квадраты заштрихованы), равна площади квадрата МКОР без суммы площадей четырёх равных треугольников, а площадь квадрата, построенного на гипотенузе (на чертеже 269 этот квадрат тоже заштрихован), равна площади квадрата М»К»О»Р», равного квадрату МКОР, без суммы площадей четырёх таких же треугольников. Следовательно, площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах.

Получаем формулу с
2 = а
2 + b
2 , где с
— гипотенуза, а
и b
— катеты прямоугольного треугольника.

Теорему Пифагора кратко принято формулировать так:

Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.

Из формулы с
2 = а
2 + b
2 можно получить такие формулы:

а
2 = с
2 — b
2 ;
b
2 = с
2 — а
2 .

Этими формулами можно пользоваться для нахождения неизвестной стороны прямоугольного треугольника по двум данным его сторонам.
Например:

а) если даны катеты а
= 4 см, b
=3 см, то можно найти гипотенузу (с
):
с
2 = а
2 + b
2 , т. е. с
2
= 4 2 + 3 2 ; с 2 = 25, откуда с
= √25
=5 (см);

б) если даны гипотенуза с
= 17 см и катет а
= 8 см, то можно найти другой катет (b
):

b
2 = с
2 — а
2 , т. е. b
2 = 17 2 — 8 2 ; b
2 = 225, откуда b
= √225
= 15 (см).

Следствие:

Если в двух прямоугольных треугольниках АВС и А 1 В 1 С 1 гипотенузы с
и с
1 равны, а катет b
треугольника АBС больше катета b
1 треугольника А 1 В 1 C 1 ,
то катет а
треугольника АВС меньше катета а
1 треугольника А 1 В 1 C 1 . (Сделать чертёж, иллюстрирующий это следствие.)

В самом деле, на основании теоремы Пифагора получим:

а
2 = с
2 — b
2 ,
а
1 2 = с
1 2 — b
1 2

В записанных формулах уменьшаемые равны, а вычитаемое в первой формуле больше вычитаемого во второй формуле, следовательно, первая разность меньше второй,
т. е. а
2 < а
1 2 . Откуда а
< а
1 .

Упражнения.

1. Пользуясь чертежом 270, доказать теорему Пифагора для равнобедренного прямоугольного треугольника.

2. Один катет прямоугольного треугольника равен 12 см, другой — 5 см. Вычислить длину гипотенузы этого треугольника.

3. Гипотенуза прямоугольного треугольника равна 10 см, один из катетов равен 8 см. Вычислить длину другого катета этого треугольника.

4. Гипотенуза прямоугольного треугольника равна 37 см, один из его катетов равен 35 см. Вычислить длину другого катета этого треугольника.

5. Построить квадрат, по площади вдвое больший данного.

6. Построить квадрат, по площади вдвое меньший данного. Указание.
Провести в данном квадрате диагонали. Квадраты, построенные на половинах этих диагоналей, будут искомыми.

7. Катеты прямоугольного треугольника соответственно равны 12 см и 15 см. Вычислить длину гипотенузы этого треугольника с точностью до 0,1 см.

8. Гипотенуза прямоугольного треугольника равна 20 см, один из его катетов равен 15 см. Вычислить длину другого катета с точностью до 0,1 см.

9. Какой длины должна быть лестница, чтобы её можно было приставить к окну, находящемуся на высоте 6 м, если нижний конец лестницы должен отстоять от здания на 2,5 м? (Черт. 271.)

Источник

Государственное
учреждение образования

«Гимназия № 38 г.
Минска»

Исследовательская
работа

по математике

«Практическое
применение теоремы Пифагора»

Выполнили:
Матвеева Алёна, 8 «Г» класс,

Бруева Элеонора, 8 «Г» класс

Руководитель:
Милевская Т.Е.

2021 год

Пояснительная
записка

«Геометрия владеет
двумя сокровищами:

одно из них – это
теорема Пифагора» Иоганн Кеплер

Актуальность: по
выражению известного ученого Иоганна Кеплера, «геометрия владеет двумя
сокровищами – теоремой Пифагора и золотым сечением, и если первое из них можно
сравнить с мерой золота, то второе – с драгоценным камнем…».

Теорема Пифагора –
одна из главных и, можно сказать, самая главная теорема геометрии. Значение ее
состоит в том, что с ее помощью можно вывести большинство теорем геометрии.

Один американский
математик, наш современник, около 20 лет собирал различные способы
доказательства теоремы Пифагора, и сейчас его «коллекция» содержит около 300
различных доказательств. Это говорит о том, что древняя теорема актуальна и
интересна людям до сих пор.

Новизна: в
школьном курсе геометрии с помощью теоремы Пифагора решаются только
математические задачи. К сожалению, вопрос о практическом применении теоремы
Пифагора не рассматривается.

В
настоящее время всеобщее признание получило то, что успех развития многих
областей науки и техники зависит от развития различных направлений математики.
Важным условием повышения эффективности производства является широкое внедрение
математических методов в технику и народное хозяйство, что предполагает
создание новых, эффективных методов качественного и количественного исследования,
которые позволяют решать задачи, выдвигаемые практикой.

Объект
исследования: теорема Пифагора.

Предмет
исследования: различные интерпретации и способы доказательства теоремы
Пифагора, ее применение при решении практических задач.

Изучая
дополнительную литературу по выбранной теме, были выдвинуты гипотезы:

1)существуют
другие интерпретации теоремы Пифагора;

2)теорема
Пифагора применяется при решении многих практических задач.

3) За красоту
и гармонию в природе «отвечает» математика. То есть, особые числовые

закономерности существуют во всем, что нас окружает.

4) С помощью
теоремы Пифагора можно решать не только математические задачи.

Цели исследования:

— внимательно
изучив формулировку теоремы Пифагора, проанализировав доказательства и
используя обобщение, рассмотреть иные интерпретации теоремы Пифагора;

— выяснить области
применения теоремы Пифагора

Для достижения
цели были поставлены следующие задачи:

1. Провести
анализ истории возникновения теоремы Пифагора и творческой деятельности
Пифагора.

2. Исследовать
различные способы доказательства и рассмотреть иные интерпретации теоремы
Пифагора.

3. Показать
практическое применение теоремы Пифагора.

Практическая
значимость:

• Использование
приобретенных знаний и навыков исследовательской работы при изучении других
школьных предметов.

• Расширение
и углубление знаний учащихся по данной теме.

• Формирование
навыков исследовательской деятельности учащихся.

• Развитие
познавательной активности учащихся, повышение интереса к предмету.

• Совершенствование
навыков работы с математической литературой.

Умения и навыки:

• Организация
и проведение эксперимента.

• Использование
специальной литературы.

• Приобретение
умения делать обзор собранного материала (доклад, презентацию, реферат).

• Оформление
работы рисунками, диаграммами, фотографиями.

• Активное
участие в обсуждении своей работы.

Оглавление

I
Введение. ……………………………………………………………………стр.4 – 5

II Основная часть…………………………………………
стр. 6 – 23

1. Немного о
Пифагоре………………………………………………………стр.6 — 8

2. История
возникновения теоремы Пифагора………………………………стр.8 — 9

3. Различные
способы доказательства теоремы Пифагора..
…………стр.10-15

4. Исторические
задачи………………………………………………………стр.15-16

5. Теорема
Пифагора в

·
строительстве
и архитектуре……………………………………………стр.17-19

·
мобильной
связи…………………………………………………………стр.20

·
литературе………………………………………………….тр.20-21

III. Заключение
…………………………………………………………………стр.22

IV. Литература…………………………………………………………………стр.23

В школьном курсе
геометрии с помощью теоремы Пифагора решаются только математические задачи. Вопрос
о практическом применении теоремы Пифагора почти не рассматривается. В
связи с этим, целью нашей работы было выяснить области применения теоремы
Пифагора.

Гипотеза:

1) Существуют
другие интерпретации теоремы Пифагора;

2) С помощью
теоремы Пифагора можно решать многие практические задачи.

Цель: выяснить
области применения теоремы Пифагора.

Задачи:

1. Собрать информацию
о практическом применении теоремы Пифагора в различных источниках и определить
области применения теоремы.

2. Изучить некоторые
исторические сведения о Пифагоре и о его теореме.

3. Показать
применение теоремы при решении исторических задач.

4. Обработать
собранные данные по теме.

5. Оформить
наработанный материал в виде проекта.

Пифагор и его
теорема

В Интернете
мы самостоятельно ознакомились с практическим применением теоремы и
историческими задачами. Вопрос о практическом применении теоремы Пифагора и о
самом Пифагоре в школьном учебнике геометрии В.В.Казакова, по которому
занимались мы, не освещен. Упоминается лишь немного о биографии Пифагора и о
том, как древние египтяне строили прямые углы с помощью веревки, разделенной на
12 равных частей (3,4,5).

Великий
ученый Пифагор родился около 570 г. до н.э. на острове Самос (откуда и пошло
прозвище Пифагор Самосский), одном из самых цветущих островов Ионии, у берега
Малой Азии, в семье богатого ювелира. Он был очень красив и с детства
отличался разумом и справедливостью. С юных лет Пифагор стремился проникнуть в
тайны Вечной Природы, постичь смысл Бытия.

Пифагор –
это греческий ученый, религиозный и политический деятель. Трудно сказать, какие
научные идеи принадлежали Пифагору, какие – его воспитанникам. Но рассказывают,
что Пифагор, доказав свою знаменитую теорему, отблагодарил богов, принеся им в
жертву 100 быков.

Другие
формулировки теоремы.

У Евклида эта
теорема гласит (дословный перевод):

«В
прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен
квадратам на сторонах, заключающих прямой угол».

В Geometria
Culmonensis (около 1400 г.) в переводе теорема читается так :

«Итак,
площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух
квадратов, которые измерены по двум сторонам его, примыкающим к прямому
углу».

Во времена
Пифагора формулировка теоремы звучала так: «Площадь квадрата, построенного
на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов,
построенных на катетах»

Современная
формулировка теоремы гласит:

«В прямоугольном
треугольнике квадрат гипотенузы равен сумме квадратов катетов»

Различные
способы доказательства теоремы Пифагора

Существует
более 500 доказательств теоремы Пифагора. Она даже занесена в книгу рекордов
Гиннеса! Простейшее доказательство теоремы есть у древнегреческого математика
Евклида. Ученые считают, что это доказательство теоремы Евклид придумал сам. В
древности, теорему Пифагора знали лишь отдельные ученые, посвященные в таинства
математики, теперь ее учат все.

Пифагором сначала
был доказан лишь частный случай теоремы: им рассматривался равнобедренный
прямоугольный треугольник. Чертеж, который используют для доказательства этого
случая, в шутку называют «пифагоровы штаны» и добавляют: во все стороны равны.

Знакомясь с
разными способами доказательства теоремы Пифагора, мы заметили, что одни из них
основаны на свойстве равносоставленных фигур, другие – на дополнении до равных
фигур, а третьи — на свойстве равновеликих фигур (имеющие равные площади).

Простейшее
доказательство теоремы получается в простейшем случае равнобедренного
прямоугольного треугольника. Например, для такого треугольника АВС: квадрат,
построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты,
построенные на катетах, — по 2. Теорема доказана.

Теорема Пифагора в
исторических задачах

Предлагаем
несколько исторических задач, найденных в древних источниках.

Задача
Бхаскари

«На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»

Решение: По
теореме Пифагора АВ²= ВС²+АС² ;9+16=25, АВ=5
Футов; СD=3+5=8 футов.
Ответ: высота тополя 8 футов.

Задача из
китайской «Математики в девяти книгах»

020601 «Имеется
водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который
выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз
коснётся его. Спрашивается: какова глубина воды, и какова длина камыша?».
Решение: По теореме Пифагора (x+1)²=x²+25; 2x=24, x=12 чи.; 12+1=13
чи.

Ответ: глубина
воды-12 чи, длина камыша-13 чи.

Задача из учебника
«Арифметика» Леонтия Магницкого 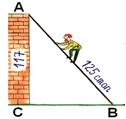020605 «Случися
некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И
обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы
нижний конец от стены отстояти имать». Решение: ВС²=АВ²-АС²;
ВС²=15625-13689=44 стоп. Ответ: ВС=44 стоп. (Приложение№3).

Теорема Пифагора
в строительстве и архитектуре

Очень
легко можно воспроизвести способ построения

«натягивателями
веревок» прямых углов при помощи прямоугольных треугольников со сторонами
3, 4 и 5. Возьмем веревку длиною в 12 м. и привяжем к ней по цветной полоске на
расстоянии 3м. от одного конца и 4
метра от другого. Прямой угол окажется заключенным

между сторонами
длиной в 3 и 4 метра.

Мы попробовали
сами применить этот метод для получения прямого угла на местности.

Строительство
крыши

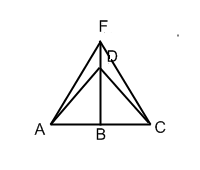
При строительстве домов и коттеджей часто встает вопрос о длине стропил для
крыши, если уже изготовлены балки. Например: в доме задумано построить
двускатную крышу (форма в сечении). Какой длины должны быть стропила, если
изготовлены балки AC=8 м., и AB=BF.      Решение:     Треугольник
ADC — равнобедренный AB=BC=4 м., BF=4 м. Если предположить, что FD=1,5 м.,
тогда из треугольника DBC: DB=2,5 м., из треугольника АВF:  АF=√4²+4²=√32≈5,7
м.

Мы знаем теперь,
что для строительства крыши дома обязательно надо применить теорему Пифагора.
При проектировании любых строительных объектов возникает необходимость
вычислять стороны прямоугольных треугольников по известным сторонам. Подобные
задачи решаются и в нашей повседневной жизни.

Теорема Пифагора в
реальной жизни

Когда мы проводили
на дачу свет, нам надо было рассчитать длину электрического провода от домика
высотой 2,5м до столба высотой 8,5м.

«Выручила»
теорема Пифагора . (Расстояние от столба до домика 8
м)

Установка ёлки

На
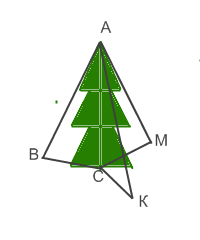
Новый год всюду устанавливают елки. Ёлка стоит неустойчиво (это проблема) и под
воздействием природных явлений (чаще сильного ветра) накреняется и может
упасть. Нужно установить ёлку высотой 8м. и закрепить её в вертикальном
положении. Для этого от вершины ёлки надо сделать проволочные натяжки АВ, АМ,
АК одинаковой длины и закрепить на земле на расстоянии 6м от основания елки.

Длина натягивающей
проволоки должна 10м., т.к. по теореме Пифагора АВ²= АС²+ВС²;

АВ==10 м.

В мобильной связи

В
настоящее время на рынке мобильной связи идет большая конкуренция среди
операторов. Чем надежнее связь, чем больше зона покрытия, тем больше
потребителей у оператора. При строительстве вышки (антенны) часто приходится
решать задачу какую наибольшую высоту должна иметь антенна, чтобы передачу
можно было принимать в определенном радиусе.

Задача: Какую
наименьшую высоту должна иметь вышка мобильной связи, поставленной в аг
Колодищи, чтобы микрорайон Уручье попал в зону связи (расстояние от вышки до Уручья
по прямой 10 км.)? Радиус Земли около 6380 км.

Решение: Применив
теорему Пифагора, получили уравнение

(х+6380)²=10²+6380²;

х²+12760х-100=0;

D=162817600+400=162818000;

≈12760,016;

х≈0,008км.

В литературе

Мало кто
знает, что Пифагор имел отношение не только к математике, но и к литературе. Он
и его теорема воспеты в литературе. О ней писали в своих произведениях римский
архитектор и инженер Витрувий, греческий писатель-моралист Плутарх, греческий
ученый III в. Диоген Лаэрций, математик V в. Прокл и многие другие.

Так, например,
немецкий писатель-романист А. Шамиссо, который в начале XIX в. участвовал в
кругосветном путешествии на корабле «Рюрик», написал следующие стихи:

Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье.

За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, ее почуя, вслед.
Они не в силах свету помешать.
А могут лишь, закрыв глаза, дрожать.

От страха, что
вселил в них Пифагор.

Теоремой
Пифагора и пифагорейской школой восхищается человечество на протяжении всей
истории, им посвящают стихи, песни, рисунки, картины.

Так художник Ф.А.
Бронников (1827-1902) нарисовал картину «Гимн пифагорейцев восходящему солнцу»

Картина передает
пафос преклонения учеников легендарной школы перед единой гармонией, царящей в
мироздании («космосе»), музыке и числе.

Практико-ориентированные
задачи:

Мы попробовали
составить свои задачи, которые можно предложить на уроке при изучении теоремы
Пифагора, чтобы подчеркнуть её практическую значимость.

Задача 1 Пожарная
лестница длиной 12,5 м приставлена к стене так, что расстояние нижнего конца
лестницы от стены равно 3,5 м. Хватит ли этой лестницы, чтобы пожарники могли
попасть в окно, находящееся на высоте 11,5 м от земли?

Задача 2
Вертикальная мачта поддерживается четырьмя канатами. Прикрепленными к ней на
расстоянии 16 м от земли и к земле на расстоянии 12 м от основания мачты.
Сколько метров каната потребовалось монтажникам для укрепления мачты, если на
узлы пошло 5 м?

Задача 3 Для
монтажа крыши, строителям надо установить стропила на балке. Какой длины надо
взять стропила, чтобы длина балки составляла 8м, а стропила образовывали прямой
угол?

Задача 4 От
столба высотой 9 м к дому электрики натянули провод, который крепится на высоте
3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину
данного провода.

Задача 5*
ПРОЕКТ

1. Определите
примерную длину лестницы, которая идёт к окну второго этажа дома, если
расстояние от этого этажа до земли 6 м, а расстояние от фундамента дома до
основания лестницы равно 3 м.

2. Подсчитайте,
сколько метров бруска пойдёт на изготовление такой лестницы, если у неё 18
ступенек и ширина лестницы равна 50 см.

3. Рассчитайте
стоимость изготовления такой лестницы, если цена 1 метра бруска составляет 6
рублей 40 коп.

Заключение

В
результате проведённого исследования мы выяснили некоторые области применения
теоремы Пифагора. Нами собрано и обработано много материала из литературных
источников и интернета по данной теме. Мы изучили некоторые исторические
сведения о Пифагоре и его теореме, решили ряд исторических задач на применение
теоремы Пифагора.

Значение теоремы
Пифагора состоит в том, что с ее помощью можно вывести большинство теорем
геометрии и решить множество задач. Благодаря такому количеству доказательств,
теорема Пифагора попала в Книгу рекордов Гиннеса, как теорема с наибольшим
количеством доказательств. Это говорит о неослабевающем интересе к ней со
стороны широкой математической общественности. Теорема Пифагора послужила
источником для множества обобщений и идей.

Результатом нашей
работы является:

1. приобретение
навыка работы с литературными источниками;

2. приобретение
навыка поиска нужного материала в Интернете;

3. научились
работать с большим объёмом информации, отбирать нужную информацию;

4. собранный
нами материал может быть полезен при изучении теоремы Пифагора в курсе
геометрии;

5. мы
подтвердили гипотезу, что теорема Пифагора имеет широкое практическое
применение.

Было
интересно почувствовать себя исследователем, но главное нас заинтересовал
процесс познания. Работа над проектом помогла нам реально применить полученные
на уроках знания, навыки, опыт в практической деятельности, в соответствии с
нашими интересами.

Скачано с www.znanio.ru

Источник

Теорема Пифагора: неизвестные доказательства

Авторы
Руководители
Файлы работы
Наградные документы

Федорова Т.С. 1

1Муниципальное бюджетное общеобразовательное учреждение «Краснооктябрьская средняя общеобразовательная школа»

Тюленева И.Ю. 1

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Прежде чем приступить к возведению

дворца вселенной,

сколько нужно еще добыть

материала из рудников опыта!

К. Гельвеций

Данная работа посвящена изучению различных доказательств теоремы Пифагора, неизвестных большинству школьников.

В настоящее время всеобщее признание получило то, что успех развития многих областей науки и техники зависит от развития различных направлений математики. Важным условием повышения эффективности производства является широкое внедрение математических методов в технику и народное хозяйство, что предполагает создание новых, эффективных методов качественного и количественного исследования, которые позволяют решать задачи, выдвигаемые практикой.

Впервые о теореме Пифагора я узнала на уроках геометрии. Задачи на эту тему давались мне очень легко. В самом деле, теорема Пифагора проста, но не очевидна. Теорема имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.) свидетельствует о гигантском числе ее конкретных реализаций, поэтому эта тема и стала основой для моего исследования. Благодаря такому количеству доказательств, теорема Пифагора попала в Книгу рекордов Гиннеса, как теорема с наибольшим количеством доказательств. Это говорит о неослабевающем интересе к ней со стороны широкой математической общественности.

Исходя из вышеизложенного, определена проблема исследования: существует множество доказательств теоремы Пифагора, однако они не рассматриваются в школьной программе. Разрешение этой проблемы в первую очередь ценностно для обучения математике учащихся средней школы.

Сформулированная проблема и определила выбор темы исследовательской работы – «Теорема Пифагора: неизвестные доказательства».

Объект исследования: теорема Пифагора.

Предмет исследования: неизвестные доказательства.

Цель работы: познакомиться с различными доказательствами теоремы Пифагора, освоить методы доказательства этой теоремы.

Гипотеза исследования: еслиизучить другие доказательства теоремы, которые не рассматриваются в школьной программе, мы убедимся в её совершенстве, красоте, простоте и особой значимости в математике.

Поставленная цель и выдвинутая гипотеза определили решение следующих задач исследования:

-изучить и проанализировать литературу о теореме Пифагора;

— определить особенности различных доказательств теоремы;

— выявить её место в математике, значимость для развития науки и области применения.

Для решения поставленных задач использовались следующие методы:

— анализ литературы по теме исследования;

— обобщение и систематизация сведений.

Работа состоит из введения, четырёх параграфов, заключения, списка используемой литературы. В первом параграфе речь идёт об истории теоремы Пифагора. Во втором параграфе рассказывается об особенностях теоремы Пифагора: различные формулировки теоремы; следствия из нее; теорема, обратная теореме Пифагора; обобщение теоремы. В третьем параграфе повествуется о различных доказательствах теоремы Пифагора, незнакомых многим школьникам. В четвёртом параграфе описываются области применения теоремы.

В работе использовано 7 источников. Наиболее ценными оказались книги: «История математики в школе» Глейзера Г. И., «Теорема Пифагора» Литцмана В., «Геометрические миниатюты» Скопеца З. А.

§1. История теоремы Пифагора

И нтересна история теоремы Пифагора. Хотя эта теорема и связана с именем Пифагора, она была известна задолго до него. В вавилонских текстах эта теорема встречается за 1200 лет до Пифагора, а в Египте это соотношение использовалось для построения прямого угла еще пять тысяч лет назад. Возможно, что тогда еще не знали ее доказательства, а само соотношение между гипотенузой и катетами было установлено опытным путем на основе измерений. Пифагор, по-видимому, нашел доказательство этого соотношения. Сохранилось древнее предание, что в честь своего открытия Пифагор принес в жертву богам быка, по другим свидетельствам – даже сто быков. На протяжении последующих веков были найдены различные другие доказательства теоремы Пифагора. Это говорит о неослабевающем интересе к ней со стороны широкой математической общественности. Теорема Пифагора послужила источником для множества обобщений и плодородных идей. Глубина этой древней истины, по-видимому, далеко не исчерпана.

И сторический обзор начнем с древнего Китая. Здесь особое внимание привлекает математическая книга Чу-пей. В этом сочинении так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5: «Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4». В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.

К рупнейший немецкий историк математики Кантор считает, что равенство 3² + 4²= 5² было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора «натягиватели веревок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.

Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой – на критическом изучении греческих источников, голландский математик Ван-дер-Варден сделал следующий вывод: «Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, является не открытие математики, но ее систематизация и обоснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку».

В настоящее время известно, что эта теорема не была открыта Пифагором. Однако одни полагают, что Пифагор первым дал ее полноценное доказательство, а другие отказывают ему и в этой заслуге. Некоторые приписывают Пифагору доказательство, которое Евклид приводит в первой книге своих «Начал».

В некоторых списках «Начал» Евклида эта теорема называлась «теоремой нимфы» за сходство чертежа с пчелкой, бабочкой, что п о-гречески называлось нимфой. Но словом этим греки называли еще некоторых богинь, а также вообще молодых женщин и невест. При переводе с греческого арабский переводчик, не обратив внимания на чертеж, перевел слово «нимфа» как «невеста», а не «бабочка». Так появилось ласковое название знаменитой теоремы – «теорема невесты».

Д оказательство теоремы Пифагора учащиеся средних веков считали очень трудным и называли его Dons asinorum – ослиный мост, или elefuga – бегство «убогих», так как некоторые «убогие» ученики, не имевшие серьезной математической подготовки, бежали от геометрии. Слабые ученики, заучившие теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста. Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли ее также «ветряной мельницей», составляли стихи, вроде «Пифагоровы штаны на все стороны равны», рисовали карикатуры.

Итак, рассматриваемая нами теорема, имеет разные названия, но в памяти школьников многих поколений хранится главное ее имя – теорема Пифагора как дань памяти великого ученого, распространившего математические знания.

§2. Особенности теоремы Пифагора

Изучая теорему Пифагора, которая отражает очень интересное соотношение между сторонами прямоугольного треугольника, обратимся к различным формулировкам теоремы, следствиям из нее, а также теоремам, связанным с ней.

Формулировки теоремы.

Приведем различные формулировки теоремы Пифагора в переводе с греческого, латинского и немецкого языков.

Во времена Пифагора теорема звучала так:

«Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах».

«Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах».

У Евклида эта теорема гласит (дословный перевод):

«В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол».

Латинский перевод арабского текста Аннаирици (около 900 г. до н. э.), сделанный Герхардом Клемонским (начало 12 в.), в переводе на русский гласит:

«Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол».

В GeometriaCulmonensis (около 1400 г.) в переводе теорема читается так:

«Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу».

В первом русском переводе евклидовых «Начал», сделанном Ф. И. Петрушевским, теорема Пифагора изложена так:

«В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол».

Существует три современные формулировки теоремы Пифагора:

1. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

2. Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах.

3. Квадрат, построенный на гипотенузе прямоугольного треугольника, равносоставлен с квадратами, построенными на катетах.

2. Теорема Пифагора имеет три следствия:

1. Если к прямой из одной точки проведены перпендикуляр и наклонная, то любая наклонная больше перпендикуляра.

2. Равные наклонные имеют равные проекции.

3. Из двух наклонных больше та, у которой проекция больше.

Теорема, обратная теореме Пифагора.

Формулировка теоремы: Если квадрат длины стороны треугольника равен сумме квадратов длин двух других сторон, то такой треугольник прямоугольный.

Докажем эту теорему.

Д ано:

Доказать:.

Доказательство теоремы.

Построим прямоугольный треугольник с катетами и . Угол – прямой. ( ; ; ).

Такой треугольник существует. В этом прямоугольном треугольнике действует прямая теорема Пифагора, то есть: .

Но по условию: .

Отсюда следует, что . Значит, .

Выясняется, что треугольники равны друг другу по трем сторонам: .

Теорема доказана.

Малоизвестное обобщение теоремы Пифагора.

Теорема Пифагора – пожалуй, самая известная из математических теорем. Сколько существует оригинальных доказательств! Сколько применений она находит в технике! Сколькими благами цивилизации мы обязаны этой великой теореме! Однако, совсем недавно, я открыла для себя совершенно новую, ранее неизвестную грань этой теоремы, которая значительно расширяет область ее применения.

Новая теорема

Итак, у нас есть все, что нужно. Прямоугольные (!) пирамиды, боковые грани-катеты и секущая грань-гипотенуза. Пришло время нарисовать еще одну картинку.

Теорема Пифагора для прямоугольной пирамиды. На картинке изображена пирамида с вершиной в начале прямоугольных координат (пирамида как бы лежит на боку). Пирамида образована тремя взаимно-перпендикулярными векторами, отложенными из начала координат вдоль координатных осей. То есть каждая боковая грань пирамиды — это прямоугольный треугольник с прямым углом при начале координат. Концы векторов определяют секущую плоскость и образуют грань-основание пирамиды.

Теорема:

П усть есть прямоугольная пирамида, образованная тремя взаимно-перпендикулярными векторами , , , у которой площади граней-катетов равны – A, B, C, и площадь грани-гипотенузы – D.

Тогда D²= A²+ B²+ C².

Альтернативная формулировка: У четырехгранной пирамиды, у которой при одной из вершин все плоские углы прямые, сумма квадратов площадей боковых граней равна квадрату площади основания.

Разумеется, если обычная теорема Пифагора формулируется для длин сторон треугольников, то новая теорема формулируется для площадей сторон пирамиды. Доказать эту теорему в трех измерениях очень просто, если вы немного знаете векторную алгебру.

Доказательство:

Выразим площади A, B, C, D через длины векторов , , ,

A = ab, B = ac, C = bс, гдеa = , b = , c = . Площадь D представим как половину площади параллелограмма, построенного на векторах и , где = – , = – .

Как известно, векторное произведение двух векторов – это вектор, длина которого численно равна площади параллелограмма, построенного на этих векторах.

Поэтому: D =

= (ab)²+ (ac)²+ (bc)² .

Таким образом, D² = (ab)²+ (ac)²+ (bc)² = A²+ B²+ C².

Что и требовалось доказать!

§3. Неизвестные доказательства теоремы

Самое простое доказательство.

С одной стороны площадь квадрата со стороной (а + b) равна (a + b)², что в результате использования формулы сокращенного умножения равно a²+ 2ab + b².

С другой стороны площадь квадрата равна сумме площадей фигур, из которых он составлен (квадрата со стороной с и 4-х равных прямоугольных треугольников с катетами а и b), а именно,

c² + 4 ab = c² + 2ab.

Значит, a²+ 2ab + b²= c² + 2ab, т.е. c² = a²+ b².

Простейшее доказательство теоремы с помощью мозаики.

П олучается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников (рис. 1), чтобы убедиться в справедливости теоремы. Например, для треугольника ABC: квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах, – по два. Теорема доказана.

Алгебраическое доказательство.

Д ано: ABC – прямоугольный треугольник,

С = 90º.

Доказать: AB²= AC²+ BC²

Доказательство:

1) Проведем высоту CD из вершины прямого угла С.

2) По определению косинуса угла соsА = AD/AC=AC/AB, отсюда следует AB AD = AC².

3) Аналогично соsВ = BD/BC=BC/AB, значит AB BD = BC².

4) Сложив почленно полученные равенства, получим:

AC²+ BC² = АВ (AD + DB).

AB²= AC² + BC².

Доказательства, основанные на использовании понятия равновеликости фигур.

П ри этом можно рассмотреть доказательства, в которых квадрат, построенный на гипотенузе данного прямоугольного треугольника «складывается» из таких же фигур, что и квадраты, построенные на катетах. Можно рассматривать и такие доказательства, в которых применяется перестановка слагаемых фигур и учитывается ряд новых идей. На рис. 2 изображено два равных квадрата. Длина сторон каждого квадрата равна a + b. Каждый из квадратов разбит на части, состоящие из квадратов и прямоугольных треугольников. Ясно, что если от площади квадрата отнять учетверенную площадь прямоугольного треугольника с катетами a, b, то останутся равные площади, т. е. c² = a² + b². Впрочем, древние индусы, которым принадлежит это рассуждение, обычно не записывали его, а сопровождали чертеж лишь одним словом: «Cмотри!» Вполне возможно, что такое же доказательство предложил и Пифагор.

Доказательство Евклида.

Д ано: ABC – прямоугольный треугольник

Доказать: S(ABDE) = S(ACFG) + S(BCHI).

Доказательство:

Пусть ABDE – квадрат, построенный на гипотенузе прямоугольного треугольника ABC, а ACFG и BCHI – квадраты, построенные на его катетах. Опустим из вершины C прямого угла перпендикуляр CP на гипотенузу и продолжим его до пересечения со стороной DE квадрата ABDE в точке Q; соединим точки C и E, B и G. Очевидно, что углы CAE и GAB равны A + 90°; отсюда следует, что треугольники ACE и AGB (закрашенные на рисунке) равны между собой (по двум сторонам и углу, заключённому между ними). Сравним далее треугольник ACE и прямоугольник PQEA; они имеют общее основание AE и высоту AP, опущенную на это основание, следовательно

S(PQEA) = 2 S(ACE).

Точно так же квадрат FCAG и треугольник BAG имеют общее основание GA и высоту AC; значит,

S(FCAG) = 2 S(GAB).

Отсюда и из равенства треугольников ACE и GBA вытекает равновеликость прямоугольника QPBD и квадрата CFGA; аналогично доказывается и равновеликость прямоугольника QPAE и квадрата CHIB. А отсюда, следует, что квадрат ABDE равновелик сумме квадратов ACFG и BCHI, т.е. теорема Пифагора.

Аддитивные доказательства.

Э ти доказательства основаны на разложении квадратов, построенных на катетах, на фигуры, из которых можно сложить квадрат, построенный на гипотенузе.

Доказательство Эйнштейна основано на разложении квадрата, построенного на гипотенузе, на 8 треугольников.

Здесь: ABC – прямоугольный треугольник с прямым углом C; CMN; CKMN; PO||MN; EF||MN.

Доказательство Хоукинсa.

П риведем еще одно доказательство, которое имеет вычислительный характер, однако сильно отличается от всех предыдущих. Оно опубликовано англичанином Хоукинсом в 1909 году; было ли оно известно до этого – трудно сказать. Прямоугольный треугольник ABC с прямым углом C повернем на 90° так, чтобы он занял положение A’CB’. Продолжим гипотенузу A’В’ за точку A’ до пересечения с линией АВ в точке D. Отрезок В’D будет высотой треугольника В’АВ. Рассмотрим теперь заштрихованный четырехугольник A’АВ’В. Его можно разложить на два равнобедренных треугольника САA’ и СВВ’ (или на два треугольника A’В’А и A’В’В).

S(CAA’) = b²/2, S(CBB’) = a²/2, S(A’AB’B) = (a² + b²)/2. Треугольники A’В’А и A’В’В имеют общее основание с и высоты DA и DB, поэтому: S(A’AB’B) = c DA/2 + c DB/2 = c (DA+DB)/2 = c²/2. Сравнивая два полученных выражения для площади, получим: a² + b² = c² Теорема доказана.

Доказательство Вальдхейма.

Это доказательство также имеет вычислительный характер. Можно использовать рисунки для доказательства, основанного на вычислении площадей двумя способами.

Д ля того чтобы доказать теорему пользуясь первым рисунком, достаточно только выразить площадь трапеции двумя путями.

Sтрапеции = (a + b)²/2

Sтрапеции = a²b² + c²/2

Приравнивая правые части получим:

a² + b² = c². Теорема доказана.

Доказательство, основанное на теории подобия.

В прямоугольном треугольника АВС проведем из вершины прямого угла высоту CD; тогда треугольник разобьется на два треугольника, также являющихся прямоугольными. Полученные треугольники будут подобны друг другу и исходному треугольнику. Это легко доказать, пользуясь первым признаком подобия (по двум углам). В самом деле, сразу видно что, кроме прямого угла, треугольники АВС и ACD имеют общий угол a, треугольники CBD и АВС – общий угол b. То, что малые треугольники также подобны друг другу, следует из того, что каждый из них подобен большому треугольнику. Впрочем, это можно установить и непосредственно.

Доказательство индийского математика Басхары.

И зображено на рисунке. В пояснение к нему он написал только одну строчку: «Смотри!». Ученые считают, что он выражал площадь квадрата, построенного на гипотенузе, как сумму площадей треугольников (4ab/2) и площадь квадрата (a-b)².

Следовательно:

c² = 4ab/2 + (a – b)²

c² = 2ab + a² – 2ab + b²

c² = a² + b².

Теорема доказана.

Луночки Гиппократа.

С уществует одно интересное приложение обобщения теоремы Пифагора, которое встречается во многих учебниках геометрии под названием теоремы о гиппократовых луночках.

Гиппократ Хиосский (вторая половина пятого века до н. э., Афины) занимался квадратурой луночек. Он называл луночкой часть плоскости, ограниченную двумя дугами окружностей. Наше предложение в том виде, как оно будет здесь сформулировано, не встречается у самого Гипократа, который нашел квадратуру только для некоторых луночек. Во всей общности теорему доказал араб Ибн Альхаитам:

» Если на гипотенузе прямоугольного треугольника как на диаметре описать полуокружность, лежащую с той же стороны гипотенузы, что и сам треугольник, то она пройдет через вершину прямого угла».

Эту теорему греки приписывали Фалесу Милетскому, но в действительности ее знали еще древние вавилоняне.

Для того, чтобы доказать теорему о гиппократовых луночках, докажем следующее предложение: Если на катетах и на гипотенузе прямоугольного треугольника построены какие угодно подобные между собой фигуры F_a, F_b, F_c, так, что катеты и гипотенуза являются сходственными отрезками этих фигур, то имеет место равенство: F_a+F_b=F_c.

Для доказательства воспользуемся следующей теоремой из теории подобия: площади подобных многоугольников относятся как квадраты сходственных сторон. Если через F_a , F_b , F_c обозначить площади подобных многоугольников, построенных на катетах a, b и гипотенузе с прямоугольного треугольника, то согласно вспомогательной теореме можно написать: Fa/Fb/Fc=a²/b²/c². Эта пропорция означает, что можно найти число k (коэффицент пропорциональности) такое, что Fa = ka², Fb = kb², Fc = kc². Умножив обе части равенства на k и принимая во внимание предыдущие равенства, получим: Fa + Fb = Fc. Если равенство Fa + Fb = Fc имеет место хотя бы для одной тройки подобных между собой многоугольников, построенных на катетах и на гипотенузе прямоугольного треугольника АВС так, что АС, ВС и АВ есть сходственные отрезки этих многоугольников, то ka² + kb² = kc² (где k имеет какое-то определенное значение, зависящее от выбора многоугольников, — нам совершенно не важно, какое именно). Но отсюда вытекает, что а² + b² = с², а это влечет за собой тот факт, что равенство Fa + Fb = Fc выполняется для любых построенных на сторонах прямоугольного треугольника подобных многоугольников, в частности, и для квадратов.

Векторное доказательство.

Пусть АВС – прямоугольный треугольник с прямым углом при вершине С, построенный на векторах. Тогда справедливо векторное равенство: b + c = a откуда имеем c = a – b возводя обе части в квадрат, получим c² = a² + b² – 2ab. Так как a перпендикулярно b, то ab = 0, откуда c² = a² + b² или c² = a² + b² Нами снова доказана теорема Пифагора. Если треугольник АВС – произвольный, то та же формула дает так называемую теорему косинусов, обобщающую теорему Пифагора.

Геометрическое доказательство методом Гарфилда.

Дано: ABC – прямоугольный треугольник.

Д оказать: BC²= AB² + AC².

Доказательство:

1) Построим отрезок CD равный отрезку AB на продолжении катета AC прямоугольного треугольника ABC. Затем опустим перпендикуляр ED к отрезку AD, равный отрезку AC, соединим точки B и E.

2) Площадь фигуры ABED можно найти, если рассматривать её как сумму площадей трёх треугольников: S(ABED) = 2*AB*AC/2+BC2/2

3) Фигура ABED является трапецией, значит, её площадь равна: S(ABED) = (DE+AB)*AD/2.

4) Если приравнять левые части найденных выражений, то получим: AB*AC+BC²/2 = (DE+AB)(CD+AC)/2, AB*AC+BC²/2 = (AC+AB)²/2 AB*AC+BC²/2 = AC²/2 + AB²/2 + AB*AC.

Доказательства методом достроения.

С ущность этого метода состоит в том, что к квадратам, построенным на катетах, и к квадрату, построенному на гипотенузе, присоединяют равные фигуры таким образом, чтобы получились равновеликие фигуры.

На рисунке изображена обычная Пифагорова фигура – прямоугольный треугольник ABC с построенными на его сторонах квадратами. К этой фигуре присоединены треугольники 1 и 2, равные исходному прямоугольному треугольнику.

Справедливость теоремы Пифагора вытекает из равновеликости шестиугольников AEDFPB и ACBNMQ. Здесь CEP, прямая EP делит шестиугольник AEDFPB на два равновеликих четырехугольника, прямая CM делит шестиугольник ACBNMQ на два равновеликих четырехугольника; поворот плоскости на 90° вокруг центра A отображает четырехугольник AEPB на четырехугольник ACMQ.

Доказательство через подобные треугольники.

П усть ABC – прямоугольный треугольник с прямым углом C. Проведём высоту из C. Обозначим её основание через H.

Треугольник ACH подобен треугольнику ABC по двум углам.

Аналогично, треугольник CBH подобен ABC.

a/c = HB/a, b/c = AH/b, т.е. a²= c*HB, b² = c*AH.

Следовательно a²+ b²= c*(HB+AH) = c². Что и требовалось доказать.

§4. Применение теоремы Пифагора

О бласть применения теоремы достаточно обширна. Теорема Пифагора даёт возможности для вычисления длин отрезков некоторых фигур на плоскости: Диагональ d квадрата со стороной а можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а.

Таким образом, d =2a².

Теорема Пифагора используется практически везде.

Молниеотвод

И звестно, что молниеотвод защищает от молнии все предметы, расстояние которых от его основания не превышает его удвоенной высоты. Необходимо определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.

Решение:

По теореме Пифагора h² ≥ a²+ b², значит, h ≥ (a² + b²)^½.

Ответ: h ≥ (a² + b²)^½.

Астрономия

Н а этом рисунке показан путь светового луча только с другой точки зрения, например из космического корабля. Предположим, что корабль движется влево. Тогда две точки, между которыми движется световой луч, станут двигаться вправо с той же скоростью. Причем, в то время, пока луч пробегает свой путь, исходная точка A смещается и луч возвращается уже в новую точку C.

Окна

В зданиях готического и романского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его очень прост: Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны ширине окна (b) для наружных дуг половине ширины, (b/2) для внутренних дуг.

Остается еще полная окружность, касающаяся четырех дуг. Т. к. она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра

Мобильная связь

В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу: Какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе (например, при радиусе R = 200 км, если известно, что радиус Земли равен 6380 км).

Решение:

Пусть АВ = х, BC = R = 200 км, ОС = r = 6380 км. ОВ = ОА + АВ, следовательно: ОВ = r + х.

Используя теорему Пифагора, получим ответ 2,3 км.

Заключение

В наши дни теорема Пифагора очень важна и актуальна. И несущественно то, что она была известна за много веков до Пифагора. Важно то, что Пифагор выделил её, дополнив собственными исследованиями, повысив значимость в мире математических открытий. Важнейшей заслугой Пифагора считается систематическое введение доказательства в математику. Только с этого момента математика и начинает существовать как наука.

Теорема Пифагора – одна из главных и, можно сказать, самая главная теорема геометрии. Она позволяет значительно расширить круг задач, решаемых в курсе геометрии и с ее помощью можно вывести большинство теорем геометрии.

К сожалению, невозможно привести все или даже самые красивые доказательства теоремы, однако приведенные примеры убедительно свидетельствуют об огромном интересе, проявляемом по отношению к ней.

Рассмотрев различные типы доказательств теоремы Пифагора, мы убедились в её совершенстве, увидев её красоту, простоту и значимость.

Список используемой литературы

Литцман В. Теорема Пифагора. М., Просвещение, 1960 г.

Еленьский Щ. По следам Пифагора. М., Учпедгиз, 1961 г

Глейзера Г. И «История математики в школе»

Скопеца З. А. «Геометрические миниатюты»

О теореме Пифагора и способах ее доказательства. http://mat.1september.ru/view_article.php?ID=200102401

Малоизвестное обобщение теоремы Пифагора. https://geektimes.ru/post/297209/

Интерактивная головоломка Теорема Пифагора. http://www.etudes.ru/ru/etudes/pythagorean-theorem/

Просмотров работы: 2574

Источник

1. Теорема Пифагора

Работа
выполнена
учениками
8 класса
МОУ Бондаревская СОШ

2. «Кто хочет изучать настоящее, не зная прошлого, тот никогда его не поймет» Г.Лейбниц

Работая в данном проекте мы
изучили биографию
древнегреческого философа и
математика Пифагора и способы
доказательства теоремы Пифагора

3. Великий ученый Пифагор родился около 570 г. до н.э.

4. ПРОБЛЕМА

В чем состоит значение теоремы
Пифагора?

5. Цели и задачи работы группы

Изучить биографию Пифагора
Изучить историю открытия теоремы
Установить какое значение имеет
открытие теоремы Пифагора в
развитие геометрии
Определить в чем заключается
рекорд теоремы Пифагора .
Рассмотреть способы доказательства
теоремы Пифагора.

6. Пифагор

Считается, что Пифагор родился в
аристократической семье на
острове Самос в Эгейском море у
берегов Малой Азии. В детстве
он получил превосходное
образование. Чтобы постичь
премудрости других народов он
путешествовал по странам
восточной части Средиземного
моря, Египту и Вавилону.

7. Пифагорейский союз

По преданию в 40 лет,
спасаясь от тирании
Поликрата Пифагор
покидает остров Самос
и уезжает в цветущий
город южной Италии,
Кротон. Пифагор и его
последователи –
пифагорейцыобразовали тайный
союз.

8. Пифагор – философ В школе Пифагора изучалось многое. Но выделялось два направления- «математиков» и «акусматиков» (акусмы-

Пифагорейские акусмы
— Что самое прекрасное? ГАРМОНИЯ
-Что самое мудрое?
ЧИСЛО
-Что самое сильное ?
РАЗУМ

9. «Все есть число»

Пифагорейцы верили, что в
числовых закономерностях
спрятана тайна мира.
Пифагор открыл, что основные
гармонические интервалы, т.е.
октава, чистая квинта и чистая
кварта, возникают, когда длины
колеблющихся струн относятся
как 2:1,3:2,4:3

10.

Пифагор – первый из
философов своего
времени удостоился,
чтобы портрет его
появился на древних
монетах

11. Пифагор -легенда

фигура Пифагора была окружена
множеством легенд:
его считали перевоплощенным богом
Аполлоном;
полагали, что у него было золотое
ребро;
он был способен преподавать в одно и
то же время в двух местах;
он мог «вызвать затмение»
при помощи цифр…изгнать болезнь

12. За легендой – истина

Открытие теоремы Пифагора окружено ореолом
красивых легенд. Прокл, комментируя последнее
предложение I книги «Начал» Евклида, пишет:
«Если послушать тех, кто любит повторять древние
легенды, то придется сказать, что эта теорема
восходит к Пифагору; рассказывают, что он в честь
этого принес в жертву быка». Легенда эта прочно
срослась с теоремой Пифагора и через 2000 лет
продолжала вызывать горячие отклики.

13. История открытия теоремы

Обычно открытие теоремы Пифагора
приписывают древнегреческому
философу и математику Пифагору
(VI в. до н. э.). Но изучение
вавилонских клинописных таблиц и
древнекитайских рукописей (копий
еще более древних манускриптов)
показало, что это утверждение было
известно задолго до Пифагора,
возможно, за тысячелетия до него.
Заслуга же Пифагора состояла в том,
что он открыл доказательство этой
теоремы.
.

14.

Трудно найти человека, у
которого имя Пифагора
не ассоциировалось бы
с его теоремой. Даже
наши бабушки и
дедушки сохранили
воспоминания о
«пифагоровых штанах».
«Пифагоровы штаны на
все стороны равны»

15.

Благодаря тому, что теорема
Пифагора позволяет находить
длину гипотенузы, не измеряя
ее непосредственно, она как
бы открывает путь с прямой на
плоскость, с плоскости в
трехмерное пространство и
дальше – в многомерные
пространства. Этим
определяется ее
исключительная важность для
геометрии и математики в
целом.

16. Теорема в стихах

Итак,
Если дан нам треугольник,
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдём:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путём
К результату мы придём.
Что и требовалось доказать

17. Способы доказательства теоремы

Доказательство теоремы
Пифагора учащиеся
средних веков считали
очень трудным и называли
его « ослиный мост», или
«бегство убогих», так как
некоторые «убогие»
ученики, не имевшие
серьезной математической
подготовки, бежали от
геометрии.
Слабые ученики, заучившие
теоремы наизусть, без
понимания и прозванные
поэтому «ослами», были не в
состоянии преодолеть теорему
Пифагора, служившую для них
вроде не преодолимого моста.
Из-за чертежей,
сопровождающих теорему
Пифагора, учащиеся называли
ее также «ветряной мельницей».

18. Существует более 500 различных доказательств теоремы Пифагора ( геометрических, алгебраических, механических и т.д.)

ПРОСТЕЙШЕЕ
ДОКАЗАТЕЛЬСТВО.
«Квадрат, построенный на
гипотенузе
прямоугольного
треугольника,
равновелик сумме
квадратов, построенных
на его катетах».

19. ДОКАЗАТЕЛЬСТВО ЕВКЛИДА

Данное доказательство
приведено в предложении 47
первой книги «Начал». На
гипотенузе и катетах
прямоугольного треугольника
АВС строятся
соответствующие квадраты (р
и доказывается, что
прямоугольник BJLD
равновелик квадрату ABFH, а
прямоугольник ICEL —
квадрату АС КС. Тогда сумма
квадратов на катетах будет
равна квадрату на гипотенузе.

20. АЛГЕБРАИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ПИФАГОРА

21. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ПИФАГОРА ЧЕРЕЗ КОСИНУС УГЛА.

Пусть АВС —
данный
прямоугольный
треугольник с
прямым углом С.
Проведем высоту
CD из вершины
прямого угла С .

22. ДОКАЗАТЕЛЬСТВО ХОУКИНСА:

23. ГЕОМЕТРИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО МЕТОДОМ ГАРФИЛДА

Дано: ABCпрямоугольный
треугольник
Доказать:
BC2=AB2+AC2

24. ПРИМЕНЕНИЕ ТЕОРЕМЫ ПИФАГОРА

Область применения
теоремы достаточно
обширна. Определим
возможности, которые дает
теорема Пифагора для
вычисления длин отрезков
некоторых фигур на
плоскости:
Диагональ d квадрата со
стороной а можно
рассматривать как
гипотенузу прямоугольного
равнобедренного
треугольника с катетом а.
Таким образом, d=2a²
Теорема Пифагора также
применяется в литературе,
мобильной связи,
архитектуре (индийцы,
например, использовали её
для построения алтарей,
которые по священному
предписанию должны иметь
геометрическую форму,
ориентированную
относительно четырех
сторон горизонта), а также в
астрономии.

25. ПИФАГОРОВЫ ТРОЙКИ.

Пифагоровы тройки –
это наборы из трёх
натуральных чисел (x,
y и z), из которых
сумма квадратов двух
чисел равна квадрату
третьего числа
Некоторые
Пифагоровы тройки:
(3, 4, 5), (6, 8, 10), (5,
12, 13), (9, 12, 15), (8,
15, 17), (12, 16, 20), (15,
20, 25), (7, 24, 25), (10,
24, 26), (20, 21, 29), (18,
24, 30), (10, 30, 34), (21,
28, 35), (12, 35, 37), (15,
36, 39), (24, 32,

26.

Спасибо за урок

Источник

Через подобные треугольники

Доказательства методом площадей

Доказательство через равнодополняемость

Доказательства через равносоставленность

Доказательство Евклида

Доказательство Леонардо да Винчи

О теореме Пифагора и способах ее доказательства

Доказательства, основанные на использовании понятия равновеликости фигур.

Аддитивные доказательства.

Доказательства методом достроения.

Алгебраический метод доказательства.

Из истории вопроса

Доказательства теоремы Пифагора

Доказательство 1

Доказательство 2

Доказательство 3

Доказательство 4

Доказательство 5

Пару слов о Пифагоровых тройках

Практическое применение теоремы

Заключение

Краткий обзор биографии

Рождение теоремы

Теорема Пифагора

Способ первый

Способ два: подобные треугольники

Еще одна методика расчетов

Самый простой способ доказать теорему Пифагора. Отзывы

Доказательство Дж. Гарфилда

Практическое применение теоремы Пифагора

Связь теоремы и астрономии

Радиус передачи мобильного сигнала

Теорема Пифагора в быту

История теоремы Пифагора

Из жизни Пифагора

В плену царя Вавилона

Тайный монашеский орден

Учение Пифагора

Теорема Пифагора

Кратко из истории теоремы Пифагора

Доказательство теоремы

Теорема Пифагора: неизвестные доказательства

1. Теорема Пифагора

2. «Кто хочет изучать настоящее, не зная прошлого, тот никогда его не поймет» Г.Лейбниц

3. Великий ученый Пифагор родился около 570 г. до н.э.

4. ПРОБЛЕМА

5. Цели и задачи работы группы

6. Пифагор

7. Пифагорейский союз

8. Пифагор – философ В школе Пифагора изучалось многое. Но выделялось два направления- «математиков» и «акусматиков» (акусмы-

9. «Все есть число»

10.

11. Пифагор -легенда

12. За легендой – истина

13. История открытия теоремы

14.

15.

16. Теорема в стихах

17. Способы доказательства теоремы

18. Существует более 500 различных доказательств теоремы Пифагора ( геометрических, алгебраических, механических и т.д.)

19. ДОКАЗАТЕЛЬСТВО ЕВКЛИДА

20. АЛГЕБРАИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ПИФАГОРА

21. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ПИФАГОРА ЧЕРЕЗ КОСИНУС УГЛА.

22. ДОКАЗАТЕЛЬСТВО ХОУКИНСА:

23. ГЕОМЕТРИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО МЕТОДОМ ГАРФИЛДА

24. ПРИМЕНЕНИЕ ТЕОРЕМЫ ПИФАГОРА

25. ПИФАГОРОВЫ ТРОЙКИ.

26.

Добавить комментарий Отменить ответ

Доказательство
Леонардо да Винчи

О теореме
Пифагора и способах ее доказательства

Доказательства, основанные
на использовании понятия равновеликости фигур.

Доказательства методом
достроения.

Алгебраический метод
доказательства.