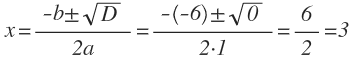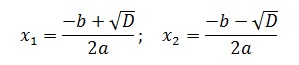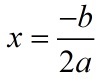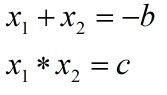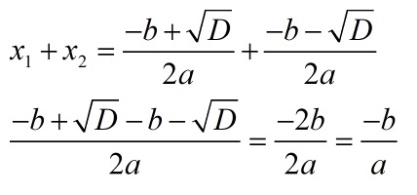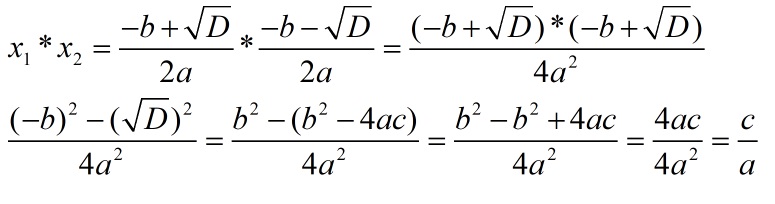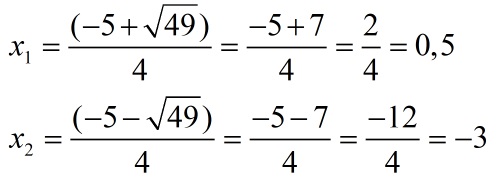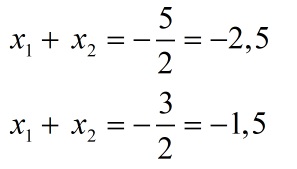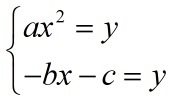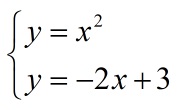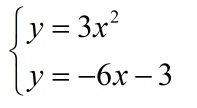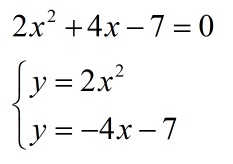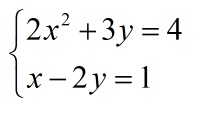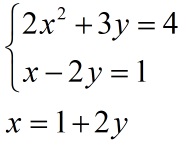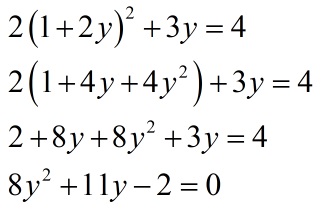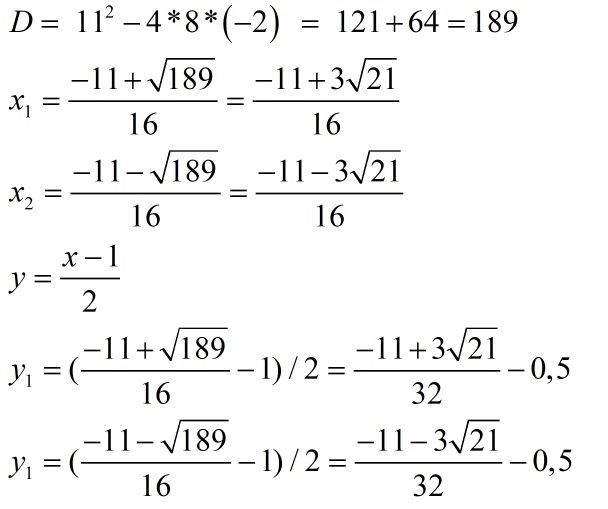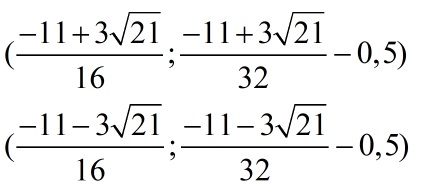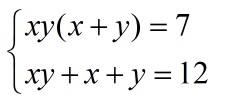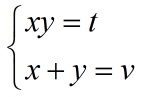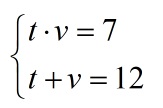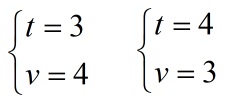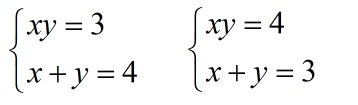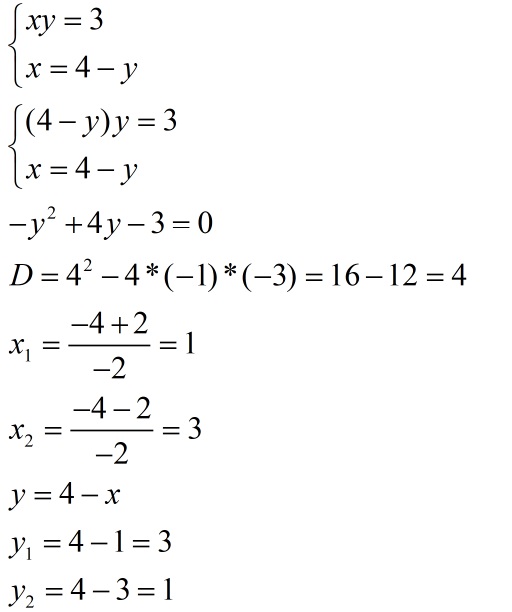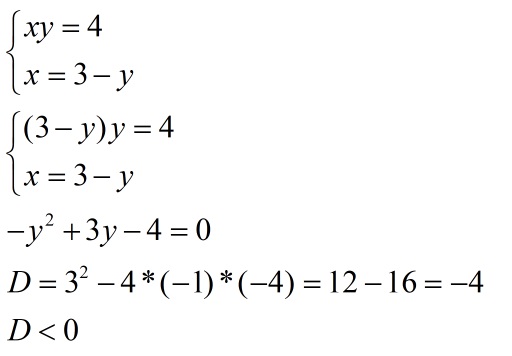8 класс алгебра дискриминант примеры для решения - Универсальный справочник

Примеры решения квадратных уравнений с ответами

Простое объяснение принципов решения квадратных уравнений и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Примеры решения квадратных уравнений с ответами обновлено: 9 марта, 2021 автором: Научные Статьи.Ру

Помощь в написании работы

Алгоритм решения квадратных уравнений

Квадратным уравнением называется уравнение вида: $ax^{2} + bx + c = 0, a neq 0$

Для решения квадратного уравнения необходимо вычислить дискриминант: $D = b^{2} - 4cdot acdot c$ .

Квадратное уравнение имеет 2 корня, если , один корень, если и не имеет корней, если .

Формулы нахождения корней квадратного уравнения.

$[x_{1,2} = frac{-bpmsqrt{b^{2} - 4cdot acdot c}}{2a}]$

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Примеры решений квадратных уравнений

Задача

Решить уравнение:

$[x^{2} - 4x + 2 = 0]$

Решение

Найдём дискриминант:

$[D = (-4)^{2} - 4cdot1cdot2 = 8]$

$[x_{1} = frac{-(-4) + sqrt{8}}{2cdot1} = frac{4 + sqrt{8}}{2}]$

$[x_{2} = frac{-(-4) - sqrt{8}}{2cdot1} = frac{4 - sqrt{8}}{2}]$

Ответ

$x_{1} = frac{4 + sqrt{8}}{2}, x_{2} = frac{4 - sqrt{8}}{2}$

Задача

Решить уравнение:

$[x^{2} - 1 = frac{x + 1}{4}]$

Решение

$[4(x^{2} - 1) = x + 1]$

$[4x^{2} - x - 5 = 0]$

Найдём дискриминант:

$[D = (-1)^{2} - 4cdot4cdot(-5) = 81]$

$[x_{1} = frac{-(-1) + sqrt{33}}{2cdot4} = frac{1 + sqrt{81}}{8}]$

$[x_{2} = frac{-(-1) - sqrt{33}}{2cdot4} = frac{1 - sqrt{81}}{8}]$

Ответ

$x_{1} = frac{1 + sqrt{81}}{8}=1,25, x_{2} = frac{1 - sqrt{81}}{8}=-1$

Задача

Решить уравнение:

$[frac{x^{2} + 1}{x - 4} - frac{x^{2} - 1}{x + 3} = 23]$

Решение

ОДЗ:

$[frac{16x^{2} - 25x -275}{(x + 3)(x - 4)} = 0]$

$[16x^{2} - 25x -275 = 0]$

$[x_{1} = frac{-(-25) + sqrt{(-25)^{2} - 4cdot16cdot(-275)}}{2cdot16} = -frac{55}{16}]$

$[x_{2} = frac{-(-25) - sqrt{(-25)^{2} - 4cdot16cdot(-275)}}{2cdot16} = 5]$

Ответ

$x_{1} = -frac{55}{16}, x_{2} = 5$

Задача

Решить уравнение:

$[frac{b}{x - a} - frac{a}{x - b} = 2]$

Решение

ОДЗ:

$[frac{2x^{2} - 3(a + b)x + (a + b)^{2}}{(x - a)(x - b)} = 0]$

$[2x^{2} - 3(a + b)x + (a + b)^{2} = 0]$

$[x_{1} = frac{-(- 3(a + b)) + sqrt{(- 3(a + b))^{2} - 4cdot2cdot(a + b)^{2}}}{2cdot2} = frac{a + b}{2}]$

$[x_{2} = frac{-(- 3(a + b)) - sqrt{(- 3(a + b))^{2} - 4cdot2cdot(a + b)^{2}}}{2cdot2} = a + b]$

Ответ

$x_{1} = frac{a + b}{2}, x_{2} = a + b$

Задача

Решить уравнение:

$[frac{x^{2} + x - 5}{x} + frac{3x}{x^{2} + x - 5} + 4 = 0]$

Решение

ОДЗ: $x neq 0, x neq frac{-1 pm sqrt{21}}{2}$

Обозначим:

$[frac{x^{2} + x - 5}{x} = z]$

Тогда:

$[z + frac{1}{z} + 4 = 0]$

$[z^{2} + 4z + 3 = 0]$

$[z_{1} = frac{-4 + sqrt{4^{2} - 4cdot1cdot3}}{2cdot1} = -3]$

$[z_{2} = frac{-4 - sqrt{4^{2} - 4cdot1cdot3}}{2cdot1} = -1]$

$[frac{x^{2} + x - 5}{x} = -3]$

$[x^{2} + 4x - 5 = 0]$

$[x_{1} = frac{-4 - sqrt{4^{2} - 4cdot1cdot(-5)}}{2cdot1} = -5]$

$[x_{2} = frac{-4 + sqrt{4^{2} - 4cdot1cdot(-5)}}{2cdot1} = 1]$

$[frac{x^{2} + x - 5}{x} = -1]$

$[x^{2} + 2x - 5 = 0]$

$[x_{3} = frac{-2 - sqrt{2^{2} - 4cdot1cdot(-5)}}{2cdot1} = - 1 - sqrt{6}]$

$[x_{4} = frac{-2 + sqrt{2^{2} - 4cdot1cdot(-5)}}{2cdot1} = -1 + sqrt{6}]$

Ответ

$x_{1} = -5, x_{2} = -1, x_{3} = - 1 - sqrt{6}, x_{4} = - 1 + sqrt{6}$

Задача

Решить уравнение:

$[x^{4} - frac{50}{2x^{4} - 7} = 14]$

Решение

ОДЗ: $x neq pm sqrt[4]{frac{7}{2}}$

Обозначим:

$[2x^{4} - 7 = z]$

Тогда:

$[frac{z + 2}{2} - frac{50}{z} = 14]$

$[z^{2} - 21z - 100 = 0]$

$[z_{1} = frac{-(-21) - sqrt{(-21)^{2} - 4cdot1cdot(-100)}}{2cdot1} = -4]$

$[z_{2} = frac{-(-21) + sqrt{(-21)^{2} - 4cdot1cdot(-100)}}{2cdot1} = 25]$

$[2x^{4} - 7 = - 4]$

$[x_{1} = -sqrt[4]{frac{3}{2}}]$

$[x_{2} = sqrt[4]{frac{3}{2}}]$

$[2x^{4} - 7 = 25]$

$[x_{3} = -2]$

$[x_{4} = 2]$

Ответ

$x_{1} = -sqrt[4]{frac{3}{2}}, x_{2} = sqrt[4]{frac{3}{2}}, x_{3} = -2, x_{4} = 2$

Задача

Решить уравнение:

$[frac{1}{x(x + 2)} - frac{1}{(x + 1)^{2}} = frac{1}{12}]$

Решение

ОДЗ:

Обозначим:

$[x^{2} + 2x = z]$

Тогда:

$[frac{1}{z} - frac{1}{z + 1} = frac{1}{12}]$

$[frac{1}{z} - frac{1}{z + 1} = 0]$

$[-z^{2} - z + 12 = 0]$

$[z_{1} = frac{-(-1) + sqrt{(-1)^{2} - 4cdot(-1)cdot12}}{2cdot(-1)} = -4]$

$[z_{2} = frac{-(-1) - sqrt{(-1)^{2} - 4cdot(-1)cdot12}}{2cdot(-1)} = 3]$

$[x^{2} + 2x = -4]$

$[x^{2} + 2x + 4 = 0]$

$D = 2^{2} - 4cdot1cdot4 = -12 < 0$ – корней нет

$[x^{2} + 2x = 3]$

$[x^{2} + 2x - 3 = 0]$

$[x_{1} = frac{-2 + sqrt{2^{2} - 4cdot1cdot(-3)}}{2cdot1} = 1]$

$[x_{2} = frac{-2 - sqrt{2^{2} - 4cdot1cdot(-3)}}{2cdot1} = -3]$

Ответ

$x_{1} = 1, x_{2} = -3$

Задача

Решить уравнение:

$[x + frac{1}{x} = 2frac{m^{2} + n^{2}}{m^{2} - n^{2}}]$

Решение

ОДЗ:

$[x_{1} = frac{m + n}{m - n}]$

$[x_{2} = frac{m - n}{m + n}]$

Ответ

$x_{1} = frac{m + n}{m - n}, x_{2} = frac{m - n}{m + n}$

Задача

Решить уравнение:

$[frac{x - 3}{x - 1} + frac{x + 3}{x + 1} = frac{x + 6}{x + 2} - frac{x - 6}{x - 2}]$

Решение

ОДЗ:

$[frac{2x^{2} - 6}{x^{2} - 1} = frac{2x^{2} - 24}{x^{2} - 4}]$

$[frac{x^{2} - 3}{x^{2} - 1} = frac{2x^{2} - 12}{x^{2} - 4}]$

$[frac{6x^{2}}{(x^{2} - 1)(x^{2} - 4)} = 0]$

Отсюда

Ответ

Задача

Решить уравнение:

$[(x - 1)(x^{2} - 3) + (2x - 1)(x^{2} + 2) = 3]$

Решение

$[x^{3} - x^{2} -3x + 3 + 2x^{3} - x^{2} + 4x - 2 = 0]$

$[3x^{3} - 2x^{2} + x - 2 = 0]$

$[3x^{3} - 3x^{2} + x^{2} - x + 2x - 2 = 0]$

$[3x^{2}(x - 1) + x(x - 1) + 2(x - 1) = 0]$

$[(x - 1)(3x^{2} + x + 2) = 0]$

$[3x^{2} + x + 2 = 0]$

$D = 1^{2} - 4cdot3cdot2 = -23 < 0$ – корней нет

Ответ

Примеры решения квадратных уравнений с ответами обновлено: 9 марта, 2021 автором: Научные Статьи.Ру

Источник

Решение квадратных уравнений

6 июля 2011

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

Не имеют корней;
Имеют ровно один корень;
Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.

Дискриминант

Пусть дано квадратное уравнение ax² + bx + c = 0. Тогда дискриминант — это просто число D = b² − 4ac.

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

Если D < 0, корней нет;
Если D = 0, есть ровно один корень;
Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

x² − 8x + 12 = 0;

5x² + 3x + 7 = 0;

x² − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)² − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3² − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)² − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D < 0, корней нет — ничего считать не надо.

Задача. Решить квадратные уравнения:

x² − 2x − 3 = 0;

15 − 2x − x² = 0;

x² + 12x + 36 = 0.

Первое уравнение:
x² − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)² − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x² = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2)² − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

[begin{align} & {{x}_{1}}=frac{2+sqrt{64}}{2cdot left( -1 right)}=-5; \ & {{x}_{2}}=frac{2-sqrt{64}}{2cdot left( -1 right)}=3. \ end{align}]

Наконец, третье уравнение:
x² + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12² − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

[x=frac{-12+sqrt{0}}{2cdot 1}=-6]

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

x² + 9x = 0;
x² − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax² + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax² = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax² + c = 0. Немного преобразуем его:

Решение неполного квадратного уравнения

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:

Если в неполном квадратном уравнении вида ax² + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
Если же (−c/a) < 0, корней нет.

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x² и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax² + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

x² − 7x = 0;

5x² + 30 = 0;

4x² − 9 = 0.

x² − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x₁ = 0; x₂ = −(−7)/1 = 7.

5x² + 30 = 0 ⇒ 5x² = −30 ⇒ x² = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x² − 9 = 0 ⇒ 4x² = 9 ⇒ x² = 9/4 ⇒ x₁ = 3/2 = 1,5; x₂ = −1,5.

Смотрите также:

Теорема Виета
Следствия из теоремы Виета
Тест на тему «Значащая часть числа»
Метод коэффициентов, часть 1
Однородные тригонометрические уравнения: общая схема решения
Задача B4: строительные бригады

Источник

Как найти дискриминант квадратного уравнения

О чем эта статья:

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, содержащее переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим:

13 = 12 — противоречие.

Значит, х = 5 не является корнем уравнения.

Если же х = 4, то при подстановке в уравнение мы получим:

12 = 12 — верное равенство.

Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Если все коэффициенты в уравнении отличны от нуля, то уравнение называется полным.

Такое уравнение можно решить с помощью формулы дискриминанта.

Понятие дискриминанта

Дискриминант квадратного уравнения — это выражение, равное b 2 − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.

Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.

Как решать квадратные уравнения через дискриминант

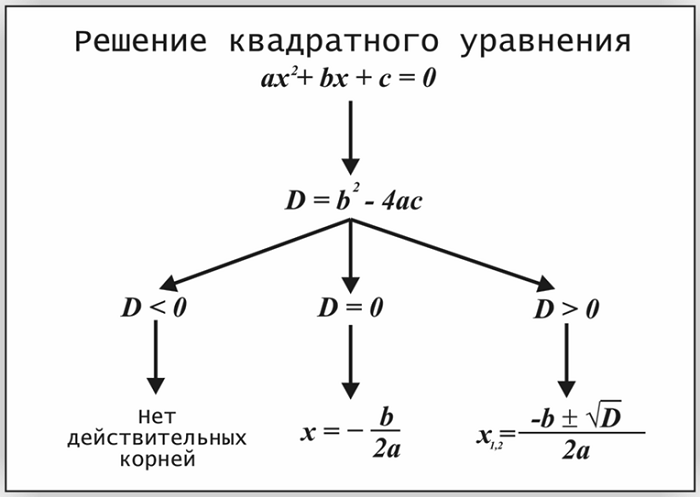
Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

Определим, чему равны коэффициенты a, b, c.

Вычислим значение дискриминанта по формуле D = b2 − 4ac.

Если дискриминант D 0, то у уравнения две корня, равные

Чтобы запомнить алгоритм решения полных квадратных уравнений и с легкостью его использовать, сохраните себе шпаргалку:

Примеры решения квадратных уравнений с помощью дискриминанта

Пример 1. Решить уравнение: 3x 2 – 4x + 2 = 0.

Определим коэффициенты: a = 3, b = -4, c = 2.
Найдем дискриминант: D = b 2 – 4ac = (-4) 2 – 4 * 3 * 2 = 16 – 24 = -8.

Ответ: D 2 – 6x + 9 = 0.

Определим коэффициенты: a = 1, b = -6, c = 9.
Найдем дискриминант: D = b 2 – 4ac = (-6) 2 – 4 * 1 * 9 = 36 – 36 = 0.

D = 0, значит уравнение имеет один корень:

Ответ: корень уравнения 3.

Пример 3. Решить уравнение: x 2 – 4x – 5 = 0.

Определим коэффициенты: a = 1, b = -4, c = -5.
Найдем дискриминант: D = b 2 – 4ac = (-4) 2 – 4 * 1 * (-5) = 16 + 20 = 36.

D > 0, значит уравнение имеет два корня:

Ответ: два корня x₁ = 5, x₂ = -1.

Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.

Квадратные уравнения (8 класс)

Уравнение называют квадратным, если его можно записать в виде (ax^2+bx+c=0), где (x) неизвестная, (a), (b) и (с) коэффициенты (то есть, некоторые числа, причем (a≠0)).

В первом примере (a=3), (b=-26), (c=5). В двух других (a),(b) и (c) не выражены явно. Но если эти уравнения преобразовать к виду (ax^2+bx+c=0), они обязательно появятся.

Коэффициент (a) называют первым или старшим коэффициентом, (b) – вторым коэффициентом, (c) – свободным членом уравнения.

Виды квадратных уравнений

Если в квадратном уравнении присутствуют все три его члена, его называют полным. В ином случае уравнение называется неполным.

Как решать квадратные уравнения

В данной статье мы рассмотрим вопрос решения полных квадратных уравнений. Про решение неполных – смотрите здесь .

Итак, стандартный алгоритм решения полного квадратного уравнения:

Преобразовать уравнение к виду (ax^2+bx+c=0).

Выписать значения коэффициентов (a), (b) и (c).
Пока не отработали решение квадратных уравнений до автоматизма, не пропускайте этот этап! Особенно обратите внимание, что знак перед членом берется в коэффициент. То есть, для уравнения (2x^2-3x+5=0), коэффициент (b=-3), а не (3).

Вычислить значение дискриминанта по формуле (D=b^2-4ac).

Решите квадратное уравнение (2x(1+x)=3(x+5))
Решение:

Теперь переносим все слагаемые влево, меняя знак.

Уравнение приняло нужный нам вид. Выпишем коэффициенты.

Найдем дискриминант по формуле (D=b^2-4ac).

Найдем корни уравнения по формулам (x_1=frac<-b + sqrt><2a>) и (x_2=frac<-b — sqrt><2a>).

Решите квадратное уравнение (x^2+9=6x)
Решение:

Тождественными преобразованиями приведем уравнение к виду (ax^2+bx+c=0).

Найдем дискриминант по формуле (D=b^2-4ac).

Найдем корни уравнения по формулам (x_1=frac<-b + sqrt><2a>) и (x_1=frac<-b — sqrt><2a>).

В обоих корнях получилось одинаковое значение. Нет смысла писать его в ответ два раза.

Решите квадратное уравнение (3x^2+x+2=0)
Решение:

Уравнение сразу дано в виде (ax^2+bx+c=0), преобразования не нужны. Выписываем коэффициенты.

Найдем дискриминант по формуле (D=b^2-4ac).

Найдем корни уравнения по формулам (x_1=frac<-b + sqrt><2a>) и (x_1=frac<-b — sqrt><2a>).

Оба корня невычислимы, так как арифметический квадратный корень из отрицательного числа не извлекается.

Обратите внимание, в первом уравнении у нас два корня, во втором – один, а в третьем – вообще нет корней. Это связано со знаком дискриминанта (подробнее смотри тут ).

Также многие квадратные уравнения могут быть решены с помощью обратной теоремы Виета . Это быстрее, но требует определенного навыка.

Пример. Решить уравнение (x^2-7x+6=0).
Решение: Согласно обратной теореме Виета, корнями уравнения будут такие числа, которые в произведении дадут (6), а в сумме (7). Простым подбором получаем, что эти числа: (1) и (6). Это и есть наши корни (можете проверить решением через дискриминант).
Ответ: (x_1=1), (x_2=6).

Данную теорему удобно использовать с приведенными квадратными уравнениями, имеющими целые коэффициенты (b) и (c).

Квадратное уравнение. Дискриминант. Теорема Виета.

теория по математике 📈 уравнения

Уравнение вида ax 2 +bx+c=0, где a,b,c – любые числа, причем a≠0, называют квадратным уравнением. Числа a,b,c принято называть коэффициентами, при этом a – первый коэффициент, b – второй коэффициент, c – свободный член.

Квадратное уравнение может иметь не более двух корней. Решить такое уравнение – это значит найти все его корни или доказать, что их нет.

Дискриминант

Количество корней квадратного уравнения зависит от такого элемента, как дискриминант (обозначают его буквой D).

Нахождение корней квадратного уравнения

Дискриминант – это такой математический инструмент, который позволяет нам определять количество корней. Он выражается определенной формулой:

D=b 2 –4ac

Если D>0, то уравнение имеет два различных

Корень – осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Пример №1. Решить уравнение х 2 –2х–3=0. Определяем коэффициенты: а=1, b=–2, c=–3. Находим дискриминант: D=b 2 –4ac=(–2) 2 –41(–3)=4+12=16. Видим, что дискриминант положительный, значит, уравнение имеет два различных корня, находим их:

Пример №2. Решить уравнение 5х 2 +2х+1=0. Определяем коэффициенты: а=5, b=2, c=1. D=b 2 –4ac=2 2 –4=4–20=–16, D 2 –6х+9=0. Определяем коэффициенты: а=1, b=–6, c=9.

D=b 2 –4ac=(–6) 2 –4=36–36=0, D=0, 1

Теорема Виета

Среди квадратных уравнений встречаются такие, у которых первый коэффициент равен 1 (обратим внимание на пример 1 и 3), такие уравнения называются приведенными.

Приведенные квадратные уравнения можно решать не только с помощью дискриминанта, но и с помощью теоремы Виета.

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком; произведение корней равно третьему коэффициенту.

Корни с помощью данной теоремы находятся устно способом подбора. Рассмотрим это на примерах.

Пример №4. Решить уравнение х 2 –10х+21=0. Выпишем коэффициенты: а=1, b=–10, c=21. Применим теорему Виета:

Начинаем с произведения корней, которое является положительным числом, значит оба корня либо отрицательные, либо положительные. Предполагаем, что это могут быть либо 3 и 7, либо противоположные им числа. Теперь смотрим на сумму, она является положительным числом, поэтому нам подходит пара чисел 3 и 7. Проверяем: 3+7=10, 37=21. Значит, корнями данного уравнения являются числа 3 и 7.

Пример №5. Решить уравнение: х 2 +5х+4=0. Выпишем коэффициенты: а=1, b=5, c=4. По теореме Виета:

Видим, что произведение корней равно 4, значит оба корня либо отрицательные, либо положительные. Видим, что сумма отрицательная, значит, будем брать два отрицательных числа, нам подходят –1 и –4. Проверим:

Данное уравнение является квадратным. Но в его условии присутствует квадратный

Записываем обязательно в начале решения, что подкоренное выражение может быть только равным нулю или положительным числом (правило извлечения квадратного

Решаем полученное неравенство: − х ≥ − 5 , отсюда х ≤ 5 . Следовательно, для ответа мы будем выбирать значения, которые меньше или равны 5.

Решаем наше квадратное уравнение, перенося все слагаемые из правой части в левую, изменяя при этом знаки на противоположные и приводя подобные слагаемые (выражения с квадратным корнем взаимоуничтожаются):

х 2 − 2 х + √ 5 − х − √ 5 − х − 24 = 0

Получим приведенное квадратное уравнение, корни которого можно найти подбором по теореме Виета:

х 2 − 2 х − 24 = 0

Итак, корнями уравнения х 2 − 2 х − 24 = 0 будут числа -4 и 6.

Теперь выбираем корень, обращая внимание на наше ограничение на х, т.е. корень должен быть меньше или равен 5. Таким образом, запишем, что 6 – это посторонний корень, так как 6 н е ≤ 5 , а число минус 4 записываем в ответ нашего уравнения, так как − 4 ≤ 5 .

pазбирался: Даниил Романович | обсудить разбор | оценить

источники:

http://cos-cos.ru/math/121/

http://spadilo.ru/kvadratnoe-uravnenie-i-diskriminant/

Источник

Уравнение называют квадратным, если его можно записать в виде (ax^2+bx+c=0), где (x) неизвестная, (a), (b) и (с) коэффициенты (то есть, некоторые числа, причем (a≠0)).

Примеры:

(3x^2-26x+5=0)
((4-x)(4x-3)=3)
(frac{x^2}{2})(+) (frac{2x}{3})(=)(frac{x-2}{6})

Коэффициент (a) называют первым или старшим коэффициентом, (b) – вторым коэффициентом, (c) – свободным членом уравнения.

Левая часть уравнения, то есть выражение (ax^2+bx+c), является квадратным трехчленом.

Виды квадратных уравнений

Если в квадратном уравнении присутствуют все три его члена, его называют полным. В ином случае уравнение называется неполным.

Полное квадратное уравнение
(6x^2-x-2=0)
(x^2-4x+3=0)
(frac{x^2}{2}-3x+1=0)

Неполное квадратное уравнение
(5x^2=0)
(x^2-25=0)
(frac{1}{2}x^2-x=0)

Как решать квадратные уравнения

В данной статье мы рассмотрим вопрос решения полных квадратных уравнений. Про решение неполных — смотрите здесь.

Итак, стандартный алгоритм решения полного квадратного уравнения:

Преобразовать уравнение к виду (ax^2+bx+c=0).
Выписать значения коэффициентов (a), (b) и (c).
Пока не отработали решение квадратных уравнений до автоматизма, не пропускайте этот этап! Особенно обратите внимание, что знак перед членом берется в коэффициент. То есть, для уравнения (2x^2-3x+5=0), коэффициент (b=-3), а не (3).
Вычислить значение дискриминанта по формуле (D=b^2-4ac).
Вычислить корни уравнения по формулам (x_1=frac{-b + sqrt{D}}{2a}) и (x_1=frac{-b — sqrt{D}}{2a}).

Примеры:

Решите квадратное уравнение (2x(1+x)=3(x+5))
Решение:

(2x(1+x)=3(x+5))		Равносильными преобразованиями приведем уравнение к виду (ax^2+bx+c=0). Сначала раскрываем скобки.
(2x+2x^2=3x+15)		Теперь переносим все слагаемые влево, меняя знак…
(2x+2x^2-3x-15=0)		…и приводим подобные слагаемые.
(2x^2-x-15=0)		Уравнение приняло нужный нам вид. Выпишем коэффициенты.
(a=2), (b=-1), (c=-15)		Найдем дискриминант по формуле (D=b^2-4ac).
(D=(-1)^2-4·2·(-15) =1+120=121)		Найдем корни уравнения по формулам (x_1=frac{-b + sqrt{D}}{2a}) и (x_2=frac{-b — sqrt{D}}{2a}).
(x_1=frac{-(-1) + sqrt{121}}{2·2}=frac{1+11}{4}=3) (x_2=frac{-(-1) — sqrt{121}}{2·2}=frac{1-11}{4}=-2,5)		Записываем ответ:

Ответ: (x_1=3), (x_2=-2,5).

Решите квадратное уравнение (x^2+9=6x)
Решение:

(x^2+9=6x)		Тождественными преобразованиями приведем уравнение к виду (ax^2+bx+c=0).
(x^2-6x+9=0)		Выпишем коэффициенты.
(a=1), (b=-6), (c=9)		Найдем дискриминант по формуле (D=b^2-4ac).
(D=(-6)^2-4·1·9=36-36=0)		Найдем корни уравнения по формулам (x_1=frac{-b + sqrt{D}}{2a}) и (x_1=frac{-b — sqrt{D}}{2a}).
(x_1=frac{-(-6) + sqrt{0}}{2·1}=frac{6+0}{2}=3) (x_2=frac{-(-6) — sqrt{0}}{2·1}=frac{6-0}{2}=3)		В обоих корнях получилось одинаковое значение. Нет смысла писать его в ответ два раза.

Ответ: (x=3).

Решите квадратное уравнение (3x^2+x+2=0)
Решение:

(3x^2+x+2=0)		Уравнение сразу дано в виде (ax^2+bx+c=0), преобразования не нужны. Выписываем коэффициенты.
(a=3), (b=1), (c=2)		Найдем дискриминант по формуле (D=b^2-4ac).
(D=1^2-4·3·2=1-24=-23)		Найдем корни уравнения по формулам (x_1=frac{-b + sqrt{D}}{2a}) и (x_1=frac{-b — sqrt{D}}{2a}).
(x_1=frac{-1 + sqrt{-23}}{2·3}) (x_2=frac{-1- sqrt{-23}}{2·3})		Оба корня невычислимы, так как арифметический квадратный корень из отрицательного числа не извлекается.

Ответ: нет корней.

Также многие квадратные уравнения могут быть решены с помощью обратной теоремы Виета. Это быстрее, но требует определенного навыка.

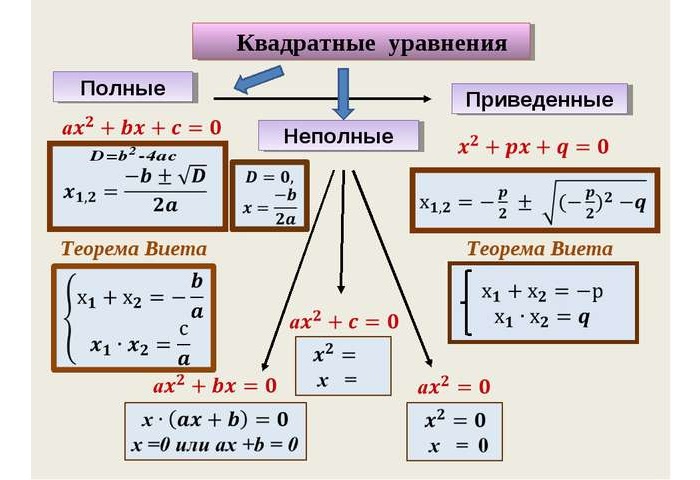
Примеры решения полных, неполных и приведенных квадратных уравнений

Смотрите также:
Квадратные уравнения (шпаргалка)

Источник

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

на главную

Дискриминант
квадратного уравнения

Поддержать сайт

Мы уже разобрали,
как решать квадратные уравнения.
Теперь давайте более подробно рассмотрим, что называют
дискриминантом квадратного уравнения.

Вернемся к нашей формуле для нахожденя корней квадратного уравнения.

Запомните!

Выражение «b² − 4ac», которое находится под корнем,
принято называть дискриминантом и обозначать буквой «D».

По-другому, через дискриминант формулу нахождения корней квадратного уравнения можно записать так:

x_1;2 = , где «D = b² − 4ac»

По одной из версий термин «Дискриминант» произошел от латинского discriminantis, что означает «отличающий» или «различающий».

В зависимости от знака «D» (дискриминанта)
квадратное уравнение может иметь два, один или ни одного корня. Рассмотрим все три случая.

I случай
D > 0
(дискриминант больше нуля)

2x² + 5x −7 = 0

D = b² − 4ac
D = 5² − 4 · 2 · (−7)
D = 25 + 56
D = 81
D > 0

x_1;2 =

x₁ =	x₂ =
x₁ =	x₂ =
x₁ = 1	x₂ = −3
x₁ = 1	x₂ = −3

Ответ: x₁ = 1;
x₂ = −3

Вывод: когда «D > 0» в квадратном уравнении два корня.

II случай
D = 0
(дискриминант равен нулю)

16x² − 8x + 1 = 0

D = b² − 4ac
D = (−8)² − 4 · 16 · 1
D = 64 − 64

D = 0

x_1;2 =

x =

Ответ: x =

Вывод: когда «D = 0» в квадратном уравнении один корень.

III случай
D < 0
(дискриминант меньше нуля)

9x² − 6x + 2 = 0

D = b² − 4ac
D = (−6)² − 4 · 9 · 2
D = 36 − 72
D = −36
D < 0

x_1;2 =

x_1;2 =

Ответ: нет действительных корней

Вывод: когда «D < 0» в квадратном уравнении нет корней.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

На чтение 7 мин. Просмотров 4.8k.

Важная характеристика квадратных уравнений — их дискриминант. По значению этой величины определяют, сколько корней у данного уравнения и есть ли они.

В 8 классе по алгебре начинают изучать квадратные уравнения и самый популярный способ их решения — через дискриминант. Формула вычисления дискриминанта известна

Дискриминант в математике используется чтобы определить сколько корней в уравнении — 1 корень, 2 корня или действительных корней нет. В этой статье определим, что такое дискриминант и выведем формулу дискриминанта.

Определение
Геометрический смысл дискриминанта
Корни квадратного уравнения через дискриминант.
- Полное квадратное уравнение
- Неполное квадратное уравнение
- Приведенное квадратное уравнение
- Если второй коэффициент кратен 2
Примеры нахождения корней уравнения с помощью дискриминанта
- Пример 1
- Пример 2
- Пример 4
  - Способ 1
  - Способ 2
- Пример 5
Выводы

Определение

Определим что такое дискриминант и зачем он нужен в математике, а также как его рассчитать.

Дискриминантом называют число, описывающее свойство коэффициентов квадратного многочлена. Хотя есть дискриминанты и кубических многочленов.

По этому числу определяют характер корней уравнения, полученному если многочлен приравнять к нулю. Так, если дискриминант больше нуля, то уравнение будет иметь два корня, равен нулю, то 1 корень, а если будет меньше нуля, то корней не будет.

Дискриминант (определение) помогает определить наличие или отсутствие корней квадратного уравнения, не решая его.

Обозначается дискриминант квадратного уравнения буквой или знаком Δ. И находится по формуле:

D=b^2-4ac , где

, и — коэффициенты уравнения:

ax^2+bx+c=0

Корни через дискриминант определяются по формулам:

displaystyle x_1=frac{-b-sqrt{D}}{2a} и displaystyle x_2=frac{-b+sqrt{D}}{2a}

Пример вычисления дискриминанта:

Вычислим дискриминант в уравнении 6x^2+4x+2=0 .

По формуле находим:

D=b^2-4ac=4^2-4cdot 6 cdot 2=16-48=-32

Мы получили отрицательный дискриминант, значит, данное уравнение не имеет действительных корней. Действительно, так как корни квадратного уравнения находят по формулам:

displaystyle x_1=frac{-b-sqrt{D}}{2a} и displaystyle x_2=frac{-b+sqrt{D}}{2a}

Подставим значения для исходного уравнения:

displaystyle x_1=frac{-4-sqrt{-32}}{12} и displaystyle x_2=frac{-4+sqrt{-32}}{12}

Как видим, мы никак не сможем посчитать корни — у нас отрицательное число под знаком радикала. И, действительно, если вы построите график функции f (x)=6x^2+4x+2 — он нигде не пересечет ось , то есть ни при каком мы не получим ноль.

График функции

Геометрический смысл дискриминанта

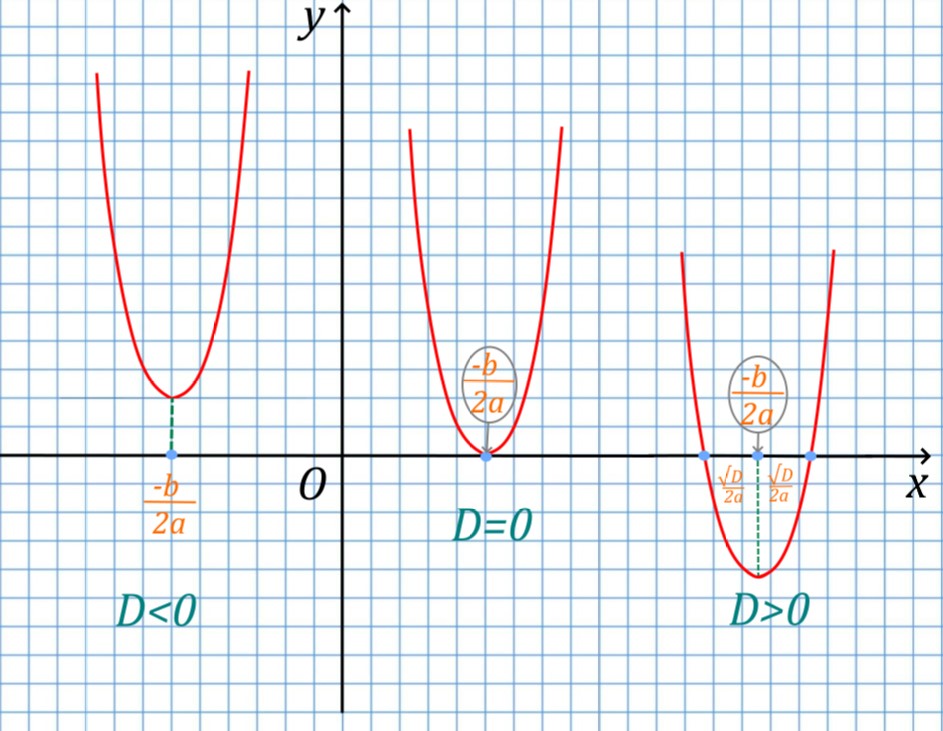
Что означает дискриминант на графике, каков его геометрический смысл? Графически дискриминант квадратного уравнения характеризует расстояние по оси абсцисс между точкой — вершиной параболы (парабола — график квадратичной функции) и точкой пересечения графика с осью абсцисс. Посмотрите на рисунок. На нем видно:

Если дискриминант равен нулю (D=0), это значит, что вершина параболы и является точкой пересечения с осью абсцисс — расстояние между точкой пересечения и вершиной параболы равно нулю.

Когда D>0, то справа и слева от точки абсцисс вершины параболы на одинаковом расстоянии displaystyle frac{sqrt{D}}{2a} будут находиться точки пересечения параболы ax^2+bx+c=y, которые являются корнями уравнения ax^2+bx+c=0.

Когда D<0 — это означает, что точек действительных отметить на оси абсцисс нельзя, то есть от вершины отложить расстояние до точек пересечения графика с осью абсцисс невозможно, то есть этих точек пересечения нет. График не пересекает ось абсцисс и корней уравнения [katex]ax^2+bx+c=0[/katex] нет.

Значение дискриминанта и его геометрический смысл

Корни квадратного уравнения через дискриминант.

Полное квадратное уравнение

Пусть нам дано уравнение вида ax^2+bx+c=0. Вычисляем дискриминант по известной формуле. Затем определяем корни уравнения.

Если D>0 получаем два вещественных корня displaystyle x_1=frac{-b-sqrt{D}}{2a} и displaystyle x_2=frac{-b+sqrt{D}}{2a}.
Если D=0 корни будут совпадать: displaystyle x_1=x_2=frac{-b}{2a}
Если D<0, вещественных корней нет, но есть мнимые корни или так называемые комплексные корни (обычно изучаются в курсе математического анализа в ВУЗах, хотя иногда и встречаются в алгебре 9-11 классов).

Неполное квадратное уравнение

Неполным называется такое квадратное уравнение, когда один из коэффициентов такого уравнения равен нулю.

Пусть коэффициент a=0, тогда уравнение сводится к линейному уравнению вида kx+b=0 и уже не будет считаться неполным.
Если равны нулю два коэффициента: и , тогда . Решением такого уравнения будет: .
Если равен нулю коэффициент b, то имеем D=-4ac и displaystyle x_1= frac{sqrt{D}}{2a} и displaystyle x_2= -frac{sqrt{D}}{2a}.
При равенстве нулю свободного члена c=0 имеем D=b^2 и displaystyle x_1=frac{-b-sqrt{D}}{2a} и displaystyle x_2=frac{-b+sqrt{D}}{2a}.

Приведенное квадратное уравнение

Приведенным квадратным уравнением называется такое уравнение вида , в котором старший коэффициент равен a=1. Оно решается обычно по теореме Виета.

Дискриминант находится по формуле: .

Если второй коэффициент кратен 2

Если коэффициент b можно разделить на 2 (с четным вторым коэффициентом), то тогда вычисляется не полный дискриминант, а displaystyle frac{D}{4} по формуле:

displaystyle frac{D}{4}=left ( frac{b}{2} right)^2-ac,

а корни: displaystyle x_1=frac{-frac{b}{2}-sqrt{frac{D}{4}}}{a} и второй корень displaystyle x_2=frac{-frac{b}{2}+sqrt{frac{D}{4}}}{a}.

Примеры нахождения корней уравнения с помощью дискриминанта

Пример 1

Решим уравнение: 4x^2+5x-5=0

Находим дискриминант: D=25-4 cdot 4 cdot (-5)=25+80=105

Корни: displaystyle x_1=frac{-5-sqrt{105}}{2cdot 4}, displaystyle x_2=frac{-5+sqrt{105}}{2cdot 4}
или

displaystyle x_1=frac{-5-sqrt{105}}{8}, displaystyle x_2=frac{-5+sqrt{105}}{8}

Пример 2

Сколько корней в данном уравнении 2x^2-3x+6=0?

Для ответа на этот вопрос необходимо найти дискриминант:

D=3^2-4 cdot 2 cdot 6=9-48=-39
D<0[/katex] — действительных корней нет.</p> <h3>Пример 3</h3> <p>[katex]x^2-6x-72=0 — найти корень.
D=b^2-4ac=(-6)^2-4 cdot (-72)=36+288=324

Так как , имеем два корня:

displaystyle x_1=frac{6-sqrt{324}}{2}, x_2=frac{6+sqrt{324}}{2}
displaystyle x_1=frac{6-18}{2}=-6, x_2=frac{6+18}{2}=12

Пример 4

Решить неполное уравнение

x^2-4=0

Способ 1

Разложим левую часть по формуле разность квадратов:

(x-2)(x+2)=0

Тогда корни:

x_1=-2, x_2=2

Способ 2

Решим задачу с помощью дискриминанта: , тогда displaystyle x_1=sqrt{D}/2=sqrt{16}/2=4/2=2,

displaystyle x_2=-sqrt{D}/2=-sqrt{16}/2=-4/2=-2

Пример 5

Придумайте такое квадратное уравнение, в котором будет нулевой дискриминант.

Решение:

Так как формула дискриминанта: D=b^2-4ac, то выберем любые коэффициенты и , а найдем, если приравняем D=b^2-4ac к нулю.

Пусть , a , тогда displaystyle D=4^2-4cdot 7cdot c=0
4^2-4cdot 7cdot c=0
16-28c=0
-28c=-16 Разделим левую и правую части на -4.

7c=4
displaystyle c=frac{4}{7}

И, получаем: displaystyle 7x^2+4x+frac{4}{7}=0

Ответ: displaystyle 7x^2+4x+frac{4}{7}=0

Выводы

Самое важное, что надо запомнить, это формулу:

D=b^2-4ac

и как определяются корни квадратного уравнения:

displaystyle x_1=frac{-b-sqrt{D}}{2a} и displaystyle x_2=frac{-b+sqrt{D}}{2a}

Можно забыть, как определяются корни в разных видах квадратных уравнений, неполных, приведенных, но если вы знаете главное — как определяется дискриминант и корни в полном квадратном уравнении, то вы сможете решить любое уравнение второй степени.

Источник

Наравне с выражениями с комплексными числами и функциями с двумя переменными, алгебра поначалу заставит ученика изрядно поломать голову вне зависимости от возраста и склада ума.;

Отчаявшиеся понять данный раздел науки могут использовать решебник и онлайн-калькулятор, выкладываемые в интернете от разных авторов в различном оформлении — на вкус читателя.

Примеры с переменной в квадрате – хорошие задания для тренировки навыков счета. В математических дисциплинах квадратное уравнение нередко выступает промежуточным шагом к доказательству теорем.

Дискриминант

Изучаемое выражение имеет стандартный вид:

ax² + bx + c = 0

Все три слагаемых имеют коэффициенты, способные принимать любые значения, но при переменной в квадрате он не должен равняться 0, иначе уравнение перестает быть квадратным.

Например, уравнение 2x²+ 2 = 0 идентично выражению 2x²+ 0x + 2 = 0.

Части равенства справа от знака равенства переносятся влево с противоположным знаком:

6x²= 8x — 4

6x²— 8x + 4 = 0

Разобрать квадратное уравнение поможет дискриминант (D). Этот вспомогательный показатель через сложные расчеты позволит найти корни выражения или обнаружить невозможность решения.

Вывод формулы выполняется благодаря манипуляции с числовыми показателями:

D = b² — 4ac

Например, в выражении 5x²— 7x + 2 = 0

D равен: (-7)²— 4*5*2 = 49 — 40 = 9.

Определение дискриминанта подскажет количество корней:

D>0: два корня;
D=0: один корень;
D<0: нет решения.

Связано это с тем, что в процессе решения дискриминант придется возводить под квадратный корень — √(D) – а отрицательные числа из него не выводятся.

Корни квадратного уравнения

Завершающий шаг – вывод ответов путем вычислений. Как решить уравнение – зависит от количества корней.

1. Если ответа 2, их нахождение выполнится через формулы:

2. Когда корень один, дискриминант уже не нужен (ведь √(0) = 0), и решать головоломку проще:

3. В случае, когда решения нет, вычислять ничего не нужно.

Далеко не все способы требуют долгих расчетов. Ученым-математиком из Франции Франсуа Виетом была выведена закономерность, раскрывающая удивительные свойства (коэффициентов):

Уникальна теорема Виета тем, что под ее определение подходят уравнения — приведенные там, где множитель при x² равен 1.

Например:

x²— 3x + 4 = 0 – приведенное;
2x²— x + 1 = 0 – неприведенное.

Сумма корней равна –b, ведь сложение x₁ и x₂ приводит к такому ответу:

Произведение обоих ответов происходит по аналогичному принципу:

Способы решения заданий с переменными в квадрате не являются специфическими – даже неприведенные выражения можно решить данной теоремой.

Как пример: 2x²— 6x + 9 = 0 при делении на коэффициент при x² (а=2) примет вид x²— 3x + 4,5 = 0 – и вполне годится для решения методикой французского ученого.

Другой метод того, как решать вариант с а≠1 – делить на a сумму и произведение корней:

2x²-5x+2=0

х₁+ х₂=5/2 =2,5

х₁* х₂=2/2 = 1

х₁=2, х₂=0,5.

Полное и неполное квадратное уравнение

Выражение ax²+ bx + c = 0 считается полным, если содержит все три коэффициента. Если есть слагаемые, равные 0, оно становится неполным.

Неполное квадратное уравнение решается гораздо легче своего полного аналога. Нахождение корней не вызывает трудностей и предполагает свои особенности в поиске ответа.

Самый простой способ – разложение на множители.

2x²— 5 x = 0 — неполное, так как с = 0.

x*(2x — 5) = 0

х₁= 0

2x — 5 = 0

х₂= 2,5.

Когда отсутствует bx, отыскать ответ еще легче:

x²— 9 = 0 (здесь b = 0)

(x+3)*(x-3) = 0

или: x²= 9

х₁= 3, х₂= -3.

Решение квадратных уравнений

Способы решения разнообразны. Состав слагаемых определяет, как находить верный ответ.

Самые легкие – разложение на множители.

Пример:

x2 + 3x — 28 = 0.

Достаточно решить, что 28 = (-4)*7, а 3х = 7х — 4х;

Многочлен x²+ 7x — 4x — 28 = 0 можно представить в виде (x + 7)(x — 4) = 0;

Только два значения способны выполнить условие равенства: -7 и 4.

Вариант сложнее – вывод формулы полного квадрата:

4x² + 8x + 4 — 4 — 32 = 0

Из 4x²+ 8x возможен многочлен 4x²+ 8x + 4, способный превратиться в (2x + 2)²

Сформировать 4x²+ 8x — 32 = 0 в более компактный вид:

4x² + 8x +4 — 4 — 32 = 0

(2x + 2)² — 36 = 0

Cвободное число переходит в правую часть:

Но не все уравнения удается преобразовать в удобную версию. Самые распространенные способы:

Стандартный алгоритм решения через дискриминант

0008

2x² + 5x — 3 = 0

Найти D:

D = 5² — 4∗2∗(-3) = 25 + 24 = 49

Вычислить корни

Теорема Виета

2x² + 5x — 3 =0

Из суммы корней и произведения образовать пропорцию

Нахождение ответов подбором и подсчетом:

-3 + 0,5 = -2,5

-3∗0,5 = -1,5

Помимо рядовых вычислений, алгебра предусматривает графический путь – минимум расчетов и чертежи на геометрической плоскости (системе координат).

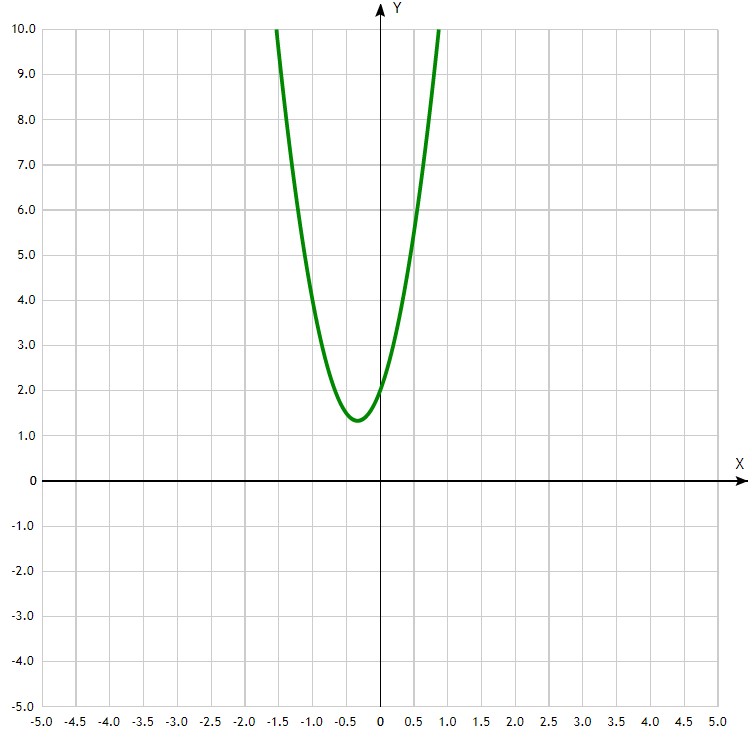
График квадратного уравнения

В отличие от рассмотренных выше вариантов, построение графика позволит наглядно решить уравнение. Здесь оно предстает в виде системы двух функций – выражений с двумя переменными.

Стандартная формула ax²+ bx + c = 0 принимает иной вид:

или ax²= -bx -c.

Общие точки параболы и линии станут ответами на задачу.

Квадратные уравнения – примеры и подробные решения

Нахождение ответа через стандартный алгоритм с дискриминантом и ее оформление в приведенное выражение уже рассмотрены, лишь графический метод нуждается в подробном рассмотрении – наглядном свидетельстве либо наличия корней, либо отсутствия оных.

Полное решение с двумя числами

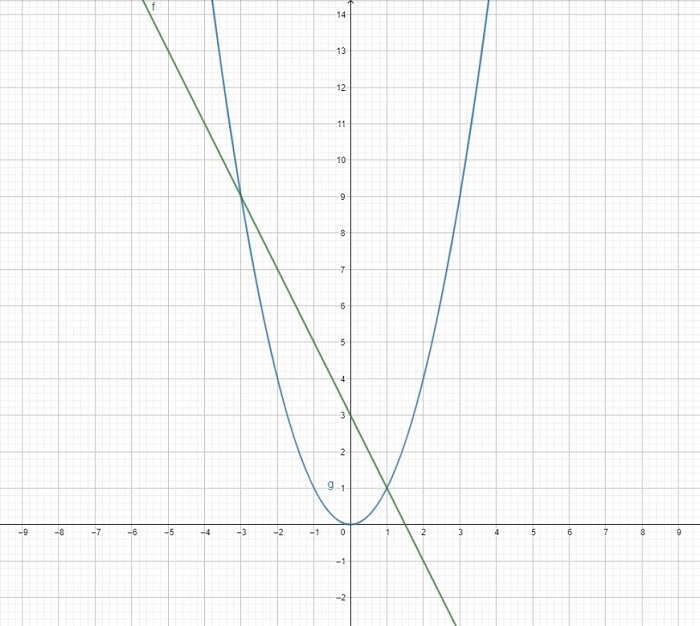
Равенство x²+ 2x — 3 = 0 аналогично удобному для графика аналогу x²= -2x + 3

На плоскость наносится система двух функций:

Пересечения графиков на точках [1;1] и [-3;9] являются решением задачи. Если нужны были данные по переменной x, воспользоваться нужно ими.

Ответ: 1 и -3.

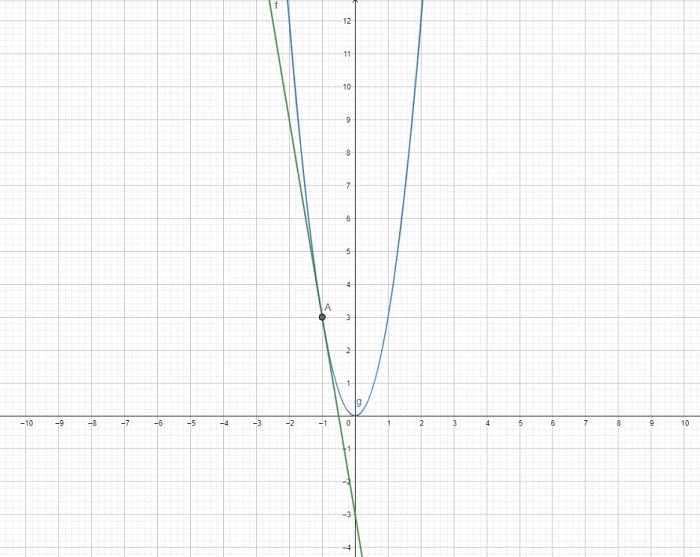
Единственный корень в уравнении

Подобно примеру выше, выражение 3x²+ 6x + 3 = 0 преобразуется в систему:

Здесь только 1 точка касается обоих графиков – [-1;3]. Координата x – корень уравнения.

Ответ: х = 1.

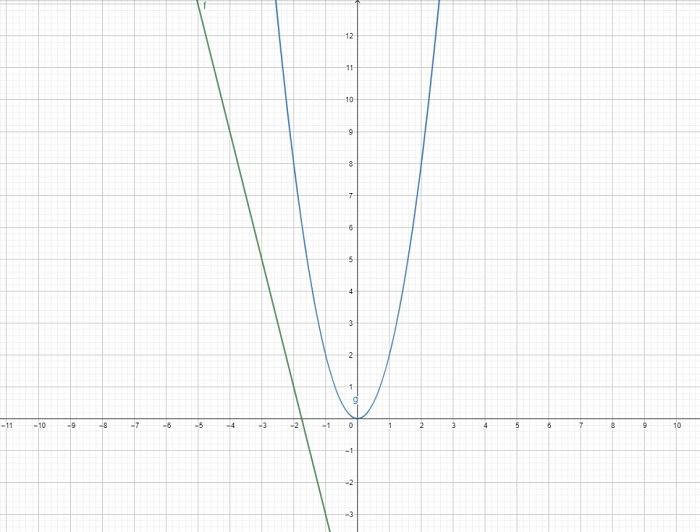
Отсутствие целевых точек

Уравнение и система

на координатной плоскости не располагают общими отметками.

Как решать случай с несовпадением графиков? Это невозможно.

Ответ: нет корней.

Как решать систему уравнений с квадратами

Квадратные уравнения с двумя переменными нередко предстают в виде системы. Их решение потребует больше усилий и времени, но нахождение ответа все еще возможно.

Первый метод уже рассмотрен в разделе выше – графический. Процесс неизменен:

Разбить уравнения на более простые.
Составить функцию с каждым на общей системе координат.
Точки пересечения станут корнями уравнения.

Второй способ – подстановка одного выражения в другое:

К системе подходит следующий алгоритм решения:

1. Представить одну переменную в составе другой:

2. Подставить выраженную переменную x в другое выражение:

3. Решить выражение как обычное квадратное уравнение:

Комбинация ответов занимает много места – дискриминант не всегда удается вывести из-под знака корня:

Третий способ – введение новых переменных. Актуален, когда подстановка займет много времени и поможет упросить вывод формулы.

Обозначить новые переменные:

Использовать их в решении, заменив ими неудобные множители:

Итог – два набора данных

или

Продолжить «расшифровку» с полученными парами чисел, создав и решив стандартное уравнение.

Первый вариант:

Здесь на выходе две подсистемы.

Второй вариант:

Корни при данном раскладе отсутствуют. Решение – первая подборка.

Ответ: х₁= (1;3), х₂= (3;1).

Источник

Примеры решения квадратных уравнений с ответами

Алгоритм решения квадратных уравнений

Примеры решений квадратных уравнений

Решение квадратных уравнений

Дискриминант

Корни квадратного уравнения

Неполные квадратные уравнения

Как найти дискриминант квадратного уравнения

Понятие квадратного уравнения

Понятие дискриминанта

Как решать квадратные уравнения через дискриминант

Примеры решения квадратных уравнений с помощью дискриминанта

Квадратные уравнения (8 класс)

Уравнение называют квадратным, если его можно записать в виде (ax^2+bx+c=0), где (x) неизвестная, (a), (b) и (с) коэффициенты (то есть, некоторые числа, причем (a≠0)).

Коэффициент (a) называют первым или старшим коэффициентом, (b) – вторым коэффициентом, (c) – свободным членом уравнения.

Виды квадратных уравнений

Если в квадратном уравнении присутствуют все три его члена, его называют полным. В ином случае уравнение называется неполным.

Как решать квадратные уравнения

Квадратное уравнение. Дискриминант. Теорема Виета.

теория по математике 📈 уравнения

Дискриминант

Теорема Виета

Уравнение называют квадратным, если его можно записать в виде (ax^2+bx+c=0), где (x) неизвестная, (a), (b) и (с) коэффициенты (то есть, некоторые числа, причем (a≠0)).

Коэффициент (a) называют первым или старшим коэффициентом, (b) – вторым коэффициентом, (c) – свободным членом уравнения.

Виды квадратных уравнений

Если в квадратном уравнении присутствуют все три его члена, его называют полным. В ином случае уравнение называется неполным.

Как решать квадратные уравнения

Примеры решения полных, неполных и приведенных квадратных уравнений

Дискриминант квадратного уравнения

I случай D > 0 (дискриминант больше нуля)

II случай D = 0 (дискриминант равен нулю)

III случай D < 0 (дискриминант меньше нуля)

Ваши комментарии

Определение

Геометрический смысл дискриминанта

Корни квадратного уравнения через дискриминант.

Полное квадратное уравнение

Неполное квадратное уравнение

Приведенное квадратное уравнение

Если второй коэффициент кратен 2

Примеры нахождения корней уравнения с помощью дискриминанта

Пример 1

Пример 2

Пример 4

Способ 1

Способ 2

Пример 5

Выводы

Дискриминант

Корни квадратного уравнения

Полное и неполное квадратное уравнение

Решение квадратных уравнений

Стандартный алгоритм решения через дискриминант

Теорема Виета

График квадратного уравнения

Квадратные уравнения – примеры и подробные решения

Полное решение с двумя числами

Единственный корень в уравнении

Отсутствие целевых точек

Как решать систему уравнений с квадратами

Добавить комментарий Отменить ответ

Дискриминант
квадратного уравнения

I случай
D > 0
(дискриминант больше нуля)

II случай
D = 0
(дискриминант равен нулю)

III случай
D < 0
(дискриминант меньше нуля)