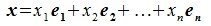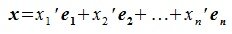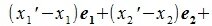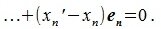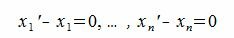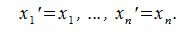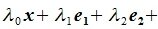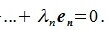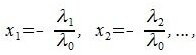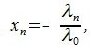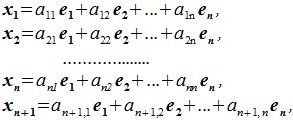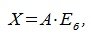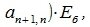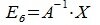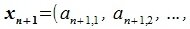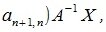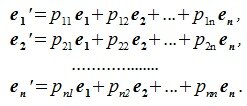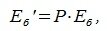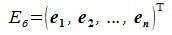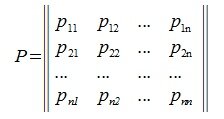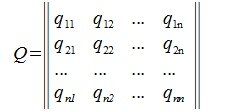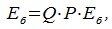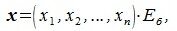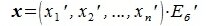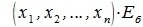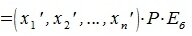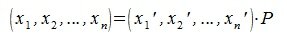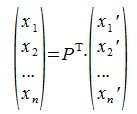Dim l линейная алгебра что это

1. Размерность линейного пространства. Две теоремы о связи размерности линейного пространства и базиса.

Определение. Линейное пространство
L называется n-мерным,
если в нем существует n
линейно независимых элементов, а любые
(n+1) элементов уже являются
линейно зависимыми. При этом число n
называют размерностью пространства L.

Размерность пространства L
обычно обозначают символ dim
L.

Определение. Линейное пространство
L называют бесконечномерным,
если в нем существует любое число линейно
независимых элементов. (dim
L=∞)

Теорема. Если линейной пространство
L – размерности n,
то любые n линейно
независимых элементов этого пространства
образуют его базис.

Доказательство.

Пусть e₁, e₂,…,
e_n –
любая система n линейно
независимых элементов пространства L
(существование хотя бы одной такой
системы вытекает из определения). Если
x – любой элемент
пространства L, то, согласно
определению система (n+1)
элементов x, e₁,
e₂,…, e_n
линейно зависима, то есть найдутся не
все равные нулю числа α₀, α₁,…,
α_n такие, что
справедливо равенство α₀x+α₁e₁+…+α_ne_n=0.
Заметим, что число α₀ заведомо
отлично от нуля (ибо в противном случае
из равенства вытекала бы линейная
зависимость элементов e₁,
e₂,…, e_n).
Но тогда поделив равенство на α₀
и положив x₁=-α₁/α₀,
x₂=-α₂/α₀,…,
x_n=-α_n/α₀,
мы получим x=x₁e₁+x₂e₂+…+x_ne_n.
Так как элемент x
произвольный элемент L,
то это равенство доказывает, что система
элементов e₁,
e₂,…, e_n
является базисом пространства L.
Теорема доказана.

Теорема. Если линейное пространство
L имеет базис, состоящий
из n элементов, то размерность
L равна n.

Доказательство. Пусть система из n
элементов e₁, e₂,…,
e_n
является базисом пространства L.
Достаточно доказать, что любые (n+1)
элементов этого пространства x₁,
x₂,…, x_n+1
линейно зависимы. разложив каждый
элемент по базису, будем иметь

x₁=α₁₁e₁+α₁₂e₂+…+α_1ne_n,

x₂=α₂₁e₁+α₂₂e₂+…+α_2ne_n,

x_n+1=α_(n+1)1e₁+α_(n+1)2e₂+…+α_(n+1)ne_n,
где α₁₁, α₁₂,…,
α_(n+1)n
– некоторые вещественные числа.

О
чевидно,
линейная зависимость элементов x₁,
x₂,…, x_n+1
эквивалента линейной зависимости строк
матрицы

α₁₁α₁₂…α_1n

A= α₂₁α₂₂…α_2n

α_(n+1)1α_(n+1)2…α_(n+1)n

Но строки указанной матрицы заведомо
линейно зависимы, ибо порядок базисного
минора этой матрицы (содержащей (n+1)
строк и n столбцов) не
превосходит n, и хотя бы
одна из (n+1) ее строк не
является базисной и по теореме о базисном
миноре представляет собой линейную
комбинацию базисных (а стало быть, и
всех остальных) строк. Теорема доказана.

(Теорема о базисном миноре – базисные
строки (базисные столбцы) линейно
независимы. Любая строка (любой столбец)
матрицы A является линейной
комбинацией базисных строк (базисных
столбцов))

1. Изоморфизм линейного пространства. Теорема об изоморфизме линейных пространств одинаковой размерности.

Определение. Два произвольных
вещественных линейных пространства L
и L^’ называются
изоморфными, если между элементами этих
пространств можно установить взаимно
однозначное соответствие так, что если
элементам x и y
пространства L отвечают
соответственно элементы x^’
и y^’ пространства
L^’, то элементу x+y
соответствует элемент x^’+y^’,
а элементу λx при любом
вещественном λ отвечает элемент λx^’.

Заметим, что если линейное пространство
L и L^’
изоморфны, то нулевому элементу L
отвечает нулевой элемент L^’
и наоборот. Если пространства L
и L^’ изоморфны, то
максимальное количество линейно
независимых элементов в каждом из этих
пространств одно и то же. Иными словами
два изоморфных пространства должны
иметь одинаковую размерность. Стало
быть пространства разной размерности
не могут быть изоморфны.

Теорема. Любые два n-мерных
вещественных линейных пространства L
и L^’ изоморфны.

Доказательство.

Выберем в L какой-нибудь
базис e₁, e₂,…,
e_n, а
в L^’ – какой-либо
базис e^’₁,
e^’₂,…, e^’_n.
Поставим в соответствие каждому элементу
x=x₁e₁+x₂e₂+…+x_ne_n
пространства L элемент
x^’=x₁e^’₁+x₂e^’₂+…+x_ne^’_n
пространства L^’
(то есть мы берем в качестве x^’
тот элемент пространства L^’,
который относительно базиса e^’₁,
e^’₂,…, e^’_n
те же самые координаты, что и элемент x
относительно базиса e₁,
e₂,…, e_n).

Убедимся в том, что установленное
соответствие является взаимно однозначным.
В самом деле, каждому элементу x
пространства L однозначно
соответствуют координаты x₁,
x₂,…, x_n,
которые в свою очередь определяют
единственный элемент x^’
пространства L^’. В
силу равноправности пространств L
и L^’ каждому элементу
x^’ пространства L^’
в свою очередь соответствует единственный
элемент x пространства L
(Соответствие между элементами двух
множеств L и L^’
называется взаимно однозначным, если
при этом соответствии каждому элементу
L отвечает один и только
один элемент L^’,
причем каждый элемент L^’
отвечает одному и только одному элементу
L). Остается заметить, что
элементам x и y
пространства L отвечают
соответственно элементы x^’
и y^’ пространства
L^’, то в силу теоремы
об операциях над элементами двух линейных
пространств, выраженных в координатах,
элементу x+y
отвечает элемент x^’+y^’,
а элементу λx отвечает
элемент λx^’. Теорема
доказана.

(Единственной существенной характеристикой
конечномерного линейного пространства
является его размерность)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Размерность и базис линейного пространства

Определения размерности и базиса

Линейное пространство называется n-мерным, если в нем существует система из линейно независимых векторов, а любая система из большего количества векторов линейно зависима. Число называется размерностью (числом измерений) линейного пространства и обозначается . Другими словами, размерность пространства — это максимальное число линейно независимых векторов этого пространства. Если такое число существует, то пространство называется конечномерным. Если же для любого натурального числа п в пространстве найдется система, состоящая из линейно независимых векторов, то такое пространство называют бесконечномерным (записывают: ). Далее, если не оговорено противное, будут рассматриваться конечномерные пространства.

Базисом n-мерного линейного пространства называется упорядоченная совокупность линейно независимых векторов (базисных векторов).

Теорема 8.1 о разложении вектора по базису. Если — базис n-мерного линейного пространства , то любой вектор может быть представлен в виде линейной комбинации базисных векторов:

и притом единственным образом, т.е. коэффициенты определяются однозначно. Другими словами, любой вектор пространства может быть разложен по базису и притом единственным образом.

Действительно, размерность пространства равна . Система векторов линейно независима (это базис). После присоединения к базису любого вектора , получаем линейно зависимую систему (так как это система состоит из векторов n-мерного пространства). По свойству 7 линейно зависимых и линейно независимых векторов получаем заключение теоремы.

Следствие 1. Если — базис пространства , то , т.е. линейное пространство является линейной оболочкой базисных векторов.

В самом деле, для доказательства равенства двух множеств достаточно показать, что включения и выполняются одновременно. Действительно, с одной стороны, любая линейная комбинация векторов линейного пространства принадлежит самому линейному пространству, т.е. . С другой стороны, любой вектор пространства по теореме 8.1 можно представить в виде линейной комбинации базисных векторов, т.е. . Отсюда следует равенство рассматриваемых множеств.

Следствие 2. Если — линейно независимая система векторов линейного пространства и любой вектор может быть представлен в виде линейной комбинации (8.4): , то пространство имеет размерность , а система является его базисом.

В самом деле, в пространстве имеется система линейно независимых векторов, а любая система из большего количества векторов линейно зависима, поскольку каждый вектор из этой системы линейно выражается через векторы . Значит, и — базис .

---

Теорема 8.2 о дополнении системы векторов до базиса. Всякую линейно независимую систему векторов n-мерного линейного пространства можно дополнить до базиса пространства.

В самом деле, пусть — линейно независимая система векторов n-мерного пространства . Рассмотрим линейную оболочку этих векторов: . Любой вектор образует с векторами линейно зависимую систему , так как вектор линейно выражается через остальные. Поскольку в n-мерном пространстве существует линейно независимых векторов, то и существует вектор , который не принадлежит . Дополняя этим вектором линейно независимую систему , получаем систему векторов , которая также линейно независимая. Действительно, если бы она оказалась линейно зависимой, то из пункта 1 замечаний 8.3 следовало, что , а это противоречит условию . Итак, система векторов линейно независимая. Значит, первоначальную систему векторов удалось дополнить одним вектором без нарушения линейной независимости. Продолжаем аналогично. Рассмотрим линейную оболочку этих векторов: . Если , то — базис и теорема доказана. Если , то дополняем систему вектором и т.д. Процесс дополнения обязательно закончится, так как пространство конечномерное. В результате получим равенство , из которого следует, что — базис пространства . Теорема доказана.

---

Замечания 8.4

1. Базис линейного пространства определяется неоднозначно. Например, если — базис пространства , то система векторов при любом также является базисом . Количество базисных векторов в разных базисах одного и того же конечномерного пространства, разумеется, одно и то же, так как это количество равно размерности пространства.

2. В некоторых пространствах, часто встречающихся в приложениях, один из возможных базисов, наиболее удобный с практической точки зрения, называют стандартным.

3. Теорема 8.1 позволяет говорить, что базис — это полная система элементов линейного пространства, в том смысле, что любой вектор пространства линейно выражается через базисные векторы.

4. Если множество является линейной оболочкой , то векторы называют образующими множества . Следствие 1 теоремы 8.1 в силу равенства позволяет говорить, что базис — это минимальная система образующих линейного пространства , так как нельзя уменьшить количество образующих (удалить хотя бы один вектор из набора ) без нарушения равенства .

5. Теорема 8.2 позволяет говорить, что базис — это максимальная линейно независимая система векторов линейного пространства, так как базис — это линейно независимая система векторов, и ее нельзя дополнить каким-либо вектором без потери линейной независимости.

6. Следствие 2 теоремы 8.1 удобно применять для нахождения базиса и размерности линейного пространства. В некоторых учебниках оно берется за определение базиса, а именно: линейно независимая система векторов линейного пространства называется базисом, если любой вектор пространства линейно выражается через векторы . Количество базисных векторов определяет размерность пространства. Разумеется, что эти определения эквивалентны приведенным выше.

---

Примеры базисов линейных пространств

Укажем размерность и базис для примеров линейных пространств, рассмотренных выше.

1. Нулевое линейное пространство не содержит линейно независимых векторов. Поэтому размерность этого пространства полагают равной нулю: . Это пространство не имеет базиса.

2. Пространства имеют размерности 1, 2, 3 соответственно. Действительно, любой ненулевой вектор пространства , образует линейно независимую систему (см. пункт 1. замечаний 8.2), а любые два ненулевых век тора пространства коллинеарны, т.е. линейно зависимы (см. пример 8.1). Следовательно, , а базисом пространства является любой ненулевой вектор. Аналогично доказывается, что и . Базисом пространства служат любые два неколлинеарных вектора, взятые в определенном порядке (один из них считается первым базисным вектором, другой — вторым). Базисом пространства являются любые три некомпланарных (не лежащих в одной или параллельных плоскостях) вектора, взятые в определенном порядке. Стандартным базисом в является единичный вектор на прямой. Стандартным базисом в считается базис , со стоящий из двух взаимно перпендикулярных единичных векторов плоскости. Стандартным базисом в пространстве считается базис , составленный из трех единичных попарно перпендикулярных векторов, образующих правую тройку.

3. Пространство содержит не более, чем , линейно независимых векторов. В самом деле, возьмем столбцов из и составим из них матрицу размеров . Если , то столбцы линейно зависимы по теореме 3.4 о ранге матрицы. Следовательно, . В пространстве не трудно найти п линейно независимых столбцов. Например, столбцы единичной матрицы

линейно независимы. Следовательно, . Пространство называется n-мерным вещественным арифметическим пространством. Указанный набор векторов считается стандартным базисом пространства . Аналогично доказывается, что , поэтому пространство называют n-мерным комплексным арифметическим пространством.

4. Напомним, что любое решение однородной системы можно представить в виде , где , a — фундаментальная система решений. Следовательно, , т.е. базисом пространства решений однородной системы служит ее фундаментальная система решений, а размерность пространства , где — количество неизвестных, а — ранг матрицы системы.

5. В пространстве матриц размеров можно выбрать 6 матриц:

которые линейно независимы. Действительно, их линейная комбинация

равна нулевой матрице только в тривиальном случае . Прочитав равенство (8.5) справа налево, заключаем, что любая матрица из линейным образом выражается через выбранные 6 матриц, т.е. . Следовательно, , а матрицы являются базисом (стандартным) этого пространства. Аналогично доказывается, что .

6. Для любого натурального в пространстве многочленов с комплексными коэффициентами можно найти п линейно независимых элементов. Например, многочлены линейно независимы, так как их линейная комбинация

равна нулевому многочлену только в тривиальном случае . Поскольку эта система многочленов линейно независима при любом натуральном л, пространство бесконечномерное. Аналогично делаем вывод о бесконечной размерности пространства многочленов с действительными коэффициентами. Пространство многочленов степени не выше, чем , конечномерное. Действительно, векторы образуют базис (стандартный) это го пространства, так как они линейно независимы и любой многочлен из можно представить в виде линейной комбинации этих векторов:

. Следовательно, .

7. Пространство непрерывных функций является бесконечно мерным. Действительно, для любого натурального многочлены , рассматриваемые как непрерывные функции, образуют линейно независимые системы (см. предыдущий пример).

В пространстве тригонометрических двучленов (частоты ) с действительными коэффициентами базис образуют одночлены . Они линейно независимы, так как тождественное равенство возможно только в тривиальном случае . Любая функция вида линейно выражается через базисные: .

8. Пространство действительных функций, определенных на множестве , в зависимости от области определения может быть конечномерным или бесконечномерным. Если — конечное множество, то пространство конечномерное (например, ). Если — бесконечное множество, то пространство бесконечномерное (например, пространство последовательностей).

9. В пространстве любое положительное число , не равное единице, может служить базисом. Возьмем, например, число . Любое положительное число можно выразить через , т.е. представить в виде , где . Следовательно, размерность этого пространства равна 1, а число является базисом.

10. Пусть — базис вещественного линейного пространства . Определим на линейные скалярные функции , положив:

При этом, в силу линейности функции , для произвольного вектора получаем .

Итак, определены элементов (ковекторов) сопряженного пространства . Докажем, что — базис .

Во-первых, покажем, что система линейно независима. В самом деле, возьмем линейную комбинацию этих ковекторов и приравняем ее нулевой функции

Подставляя в это равенство , получаем . Следовательно, система элементов пространства линейно независима, так как равенство возможно только в тривиальном случае.

Во-вторых, докажем, что любую линейную функцию можно представить в виде линейной комбинации ковекторов . Действительно, для любого вектора в силу линейности функции получаем:

т.е. функция представлена в виде линейной комбинации функций (числа — коэффициенты линейной комбинации). Следовательно, система ковекторов является базисом сопряженного пространства и (для конечномерного пространства ).

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Линейное (векторное) пространство

1. Понятие линейного пространства

Определение 1.1. Множество R элементов x, y, z, … любой природы называется линейным (или векторным) пространством, если выполнены следующие три требования:

1. Существует правило, посредством которого любым двум элементам x и y множества R ставится в соответствие третий элемент z этого множества, называемый суммой элементов x и y и обозначаемый z=x+y.
2. Существует правило, посредством которого любому элементу x множества R и любому вещественному числу α ставится в соответствие элемент w этого множества, называемый произведением элемента x на число α и обозначаемый w=αx или w=xα.
3. Представленные два правила подчинены следующим восьми аксиомам:
   1. x+y=y+x (переместительное свойство суммы);
   2. (x+y)+z=x+(y+z) (сочетательное свойство суммы);
   3. существует нулевой элемент 0 такой, что x+0=x для любого элемента x.
   4. для любого элемента x существует противоположный элемент элемент x’ такой, что x+x’=0;
   5. 1·x=x для любого x;
   6. λ(μx)=(λμ)x (сочетательное свойство относительно числового множителя);
   7. (λ+μ)x=λx+μx (распределительное свойство относительно числовых множителей);
   8. λ(x+y)=λx+λy (распределительное свойство относительно суммы элементов).

Элементы линейного (векторного) пространства называются векторами.

2. Базис линейного пространства

Определение 2.1. Совокупность линейно независимых элементов пространства R называется базисом этого пространства, если для каждого элемента x пространства R существуют вещественные чиcла такие, что выполнено равенство

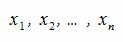
(2.1)

Равенство (2.1) называется разложением элемента x по базису а числа называются координатами элемента x (относительно базиса ).

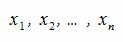
Докажем, что любой элемент x линейного пространства R может быть разложен по базису единственным образом.

Пусть существует и другое разложение x:

(2.2)

Вычитая (2.1) из (2.2) имеем:

(2.3)

Так как базисные элементы линейно независимы из соотношения (2.3) следует, что

или

Следовательно каждый элемент линейного пространства R может быть разложен по базису единственным образом.

Теорема 2.2. При сложении произвольных двух элементов линейного пространства R их координаты (относительно любого базиса пространства R) складываются, а при умножении любого элемента x на любое число α все координаты x умножаются на α.

Доказательство следует из аксиом 1-8 определения 1.1.

3. Размерность линейного пространства

Рассмотрим произвольное вещественное пространство R.

Определение 3.1. Линейное пространство R называется n-мерным, если в нем существует n линейно независимых элементов, а любые (n+1) элементов уже являются линейно зависимыми. При этом число n называется размерностью пространства R.

Размерность пространства обозначают символом dim.

Определение 3.2. Линейное пространство R называется бесконечномерным, если в нем существует любое число линейно независимых элементов.

Теорема 3.3. Пусть R является линейным пространствам размерности n (dim R=n). Тогда любые n линейно независимых элементов этого пространства образуют его базис.

Доказательство. Так как R является n -мерным пространством, то из определения 2.1 следует, что в нем существует совокупность из n линейно независимых элементов . Пусть x — любой элемент из R. Тогда согласно определению 3.1 линейно зависимы, т.е. существуют числа (не все равные нулю) такие, что справедливо равенство

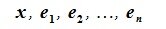
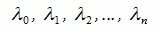
(3.1)

Заметим, что λ₀≠0 т.к. в противном случае из равенства (3.1) следовала, что элементы линейно зависимы. Поделив равенство (3.1) на λ₀ и положив

(3.2)

получим

(3.3)

Из равенства (3.3) следует, что любой вектор из пространства R может быть разложен по элементам и, следовательно, они образуют базис пространства R. ■

Теорема 3.4. Пусть линейное пространство R имеет базис, состоящий из n элементов. Тогда размерность R равна n (dim R=n).

Доказательство. Пусть множество n элементов является базисом пространства R. Достаточно доказать, что любые n+1 элементы этого пространства линейно зависимы. Разложив эти элементы по базису, получим:

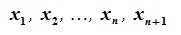
(3.4)

где a₁₁, a₁₂,…, a_n+1,n вещественные числа.

Пусть элементы 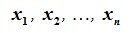линейно независимы. Перепишем (3.4) в матричном виде:

(3.5)

(3.6)

где, n×n-матрицы(элементы здесь являются вектор-строками),

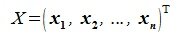
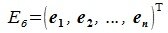
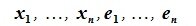
(3.7)

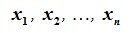
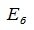
Так как линейно независимы, матрица A имеет обратную матрицу A^-1. Решив матричное уравнение (3.5) относительно получим :

(3.8)

Подставляя (3.8) в (3.6), получим:

(3.9)

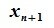
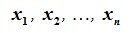
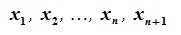
Как видно из уравнения (3.9) можно представить линейной комбинацией векторов . Следовательно векторы линейно зависимы. ■

4. Замена базиса и преобразование координат

Пусть в пространстве R наряду с исходным базисом имеется другой базис . Векторы этого базиса можно выразить через линейную комбинацию векторов исходного базиса следующим образом:

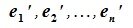
(4.1)

или

(4.2)

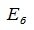
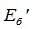
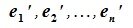
где и матрицы составленные из векторов строк и соответственно (), а матрица P имеет вид:

(4.3)

Матрица P называется матрицей замены базиса на .

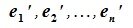
В свою очередь, векторы исходного базиса выражаются через векторы нового следующим соотношением:

(4.4)

где

(4.5)

Подставляя (4.2) в (4.4) имеем:

(4.6)

Из (4.6) следует, что QP=E, где E-единичная матрица, а матрицы Q и P взаимно обратные матрицы.

Рассмотрим как изменяются координаты векторов при замене базиса.

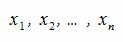
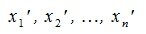
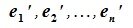
Пусть вектор x имеет координаты в базисе и координаты в базисе , тогда

(4.7)

или

(4.8)

Из (4.8) и из (4.2) имеем:

(4.9)

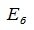
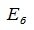
Так как квадратная матрица полного ранга, она имеет обратную матрицу. Умножив левые и правые части уравнения (4.9) на обратную к матрицу получим:

или

(4.10)

Матрица P^T называется матрицей преобразования координат. Она транспонирована с матрицей замены базиса. Обратная матрица (P^T)^-1 дает выражения новых координат через старые.

Матрица, обратная к транспонированной для некоторой матрицы, называется контраградиентной с ней.

5. Изоморфизм линейных пространств

Определение 5.1. Два произвольных вещественных линейных пространства R и R’ называются изоморфными, если между элементами этих пространств можно установить взаимно однозначное соответствие так, что если x, y∈R отвечают x’, y’∊R’ соответственно, то элементу x+y∈R отвечает элемент x’+y’∈R’, а для любого вещественного α, элементу αx∈R отвечает элемент αx’∈R’.

Теорема 5.2. Если пространства R и R’ изоморфны, то они имеют одинаковую размерность.

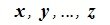
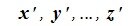
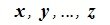
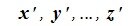
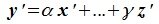
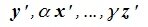
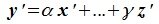
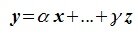
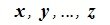
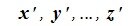
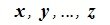
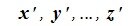
Доказательство. Пусть линейные пространства R и R’ изоморфны, и пусть элементам пространства R отвечают элементы пространства R’ соответственно. Допустим элементы линейно независимы. Покажем, что элементы также линейно независимы. Исходя из обратного предположения допустим, что элементы линейно зависимы. тогда один из них можно представить линейной комбинацией остальных элементов:. Но элементам отвечают элементы y в пространстве R, а сумме отвечает сумма . Но последнее означает линейную зависимость элементов . Следовательно линейно независимы. Из линейной зависимости элементов следует линейная зависимость элементов . Следовательно максимальное количество линейно независимых векторов для пространств R и R’ одно и то же, т.е. эти пространства имеют одинаковую размерность. ■

Теорема 5.3. Любые два n-мерных вещественных линейных пространства R и R’ изоморфны.

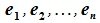
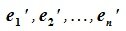
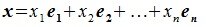
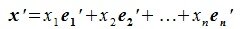
Доказательство. Выберем базисы и для пространств R и R’ соответственно. Тогда каждый элемент пространства R можно представить линейной комбинацией базисных элементов: . Этому элементу в пространстве R’ поставим в соответствие элемент теми же координатами:. В свою очередь элементу x’ пространства R’ соответствует элемент x пространства R . Отметим, что если элементам x и y пространства R отвечают элементы x’ и y’ пространства R’ соответственно , то исходя из теоремы 2.2 элементу x+y пространства R отвечает элемент x’+y’ пространства R’, а элементу αx отвечает элемент αx’. ■

Основные идеи, размышления и примеры

Этот пост взят из заметок к короткому курсу линейной алгебры, который я читал в Red Ventures в рамках нашей программы ускорителя науки о данных (вы можете узнать больше о программе здесь). Таким образом, примечания являются менее формальными и менее исчерпывающими, чем учебник, но они могут быть полезным способом получить быстрый обзор некоторых основополагающих структур для задач машинного обучения.

Обозначение

На протяжении всего курса я буду использовать некоторые обозначения, которые являются стандартными в математике, но в противном случае могут показаться очень забавными (на вкус это забавно, а не «ха-ха»). Поскольку вопросы о нотации очень сложно подобрать в Google, пожалуйста, попросите пояснений в разделе комментариев, чтобы я мог лучше объяснять себя.

Общие поля

Обычно я использую k для произвольного поля, но есть некоторые поля, которые появляются так часто, что требуют особой обработки. В большинстве документов они написаны в стиле «классной доски», но для целей этой статьи я просто буду использовать полужирный шрифт, чтобы их можно было писать в строке без отрисовки магических символов:

• Q: поле рациональных чисел — набор чисел, который может быть представлен как a / b, где a и b — целые числа.
• R: поле действительных чисел.
• C: поле комплексных чисел — набор чисел вида a + bi, где a и b — целые числа.

Итак. . . что за поле? Поле — это просто набор с хорошо выполненными операциями сложения и умножения. В частности, каждый элемент должен иметь аддитивный и мультипликативный обратный — это означает, что каждое число a имеет число, которое вы можете добавить к нему, чтобы получить 0, и число, которое вы можете умножить на него, чтобы получить 1 ( но 0 является особенным и не имеет обратного умножения). Итак, рациональные числа — это поле, а целые — нет.

Установить обозначение

Мы можем рассматривать набор S как набор объектов a, b. . . Обычно мы будем использовать «фигурные скобки» при определении множеств, т. е.

Если мы хотим выразить, что конкретный элемент s содержится в наборе S, мы напишем s ∈ S.

Иногда мы будем определять множества с помощью условий, для этого есть специальные обозначения. Например, мы могли бы определить набор рациональных чисел как:

который можно было бы читать так: «Определите Q как набор элементов x в R, удовлетворяющих свойству, которое x = a / b для некоторых a и b в наборе целых чисел Z .

Для данного набора S мы можем захотеть сослаться на количество элементов в S (или мощность S), обозначенное | S |. Это просто для конечных множеств, но может быть немного странным для бесконечных множеств. Мы не будем спорить о разной мощности бесконечных множеств, хотя может быть интересно подумать об этом, если вы занимаетесь такими вещами.

Функции

Функция — это карта между множествами. Формально, если A и B заданы, то функция от A до B (написано f : A → B) — это набор:

со свойством, что если (a, b) ∈ f и (a, b ’) ∈ f, то b = b’. (В начальной школе это свойство часто называют «тестом вертикальной линии»). Однако мы почти никогда не думаем о f как о множестве — мы обычно думаем об этом как о правиле присваивания: if (a, b) ∈ f, мы говорим, что f отображает a в b, записывается f (a) = b или a ↦ b.

Другие обозначения

Для понимания нескольких примеров в этих заметках потребуется немного больше времени, или они будут более неясными. Я обозначу эти примеры или замечания знаком, например, осторожно, это резковато, не порежься!

Размышления и обрамления

В наши дни в математике одной полезной концепцией для понимания определенных идей (может быть, это топологические пространства, группы или гладкие многообразия) является категориальная перспектива. Категория C грубо говоря — это набор объектов O и набор морфизмов (или стрелок) M. o.

Таким образом мы часто можем обнажить гораздо большую часть структуры, чем если бы мы просто прищурились от самих объектов. (На самом деле это не новая или новая идея, ученые используют ее постоянно — если вы хотите понять что-то новое, очень часто полезно наблюдать, как это взаимодействует с известными величинами.)

Вторая тактика — перевести анализ в более простую категорию с помощью так называемого функтора C → C ’. Это имеет очень точное значение в математике, и его применение привело к скачку вперед в этой области. В науке о данных мы применяем это в духе — проблема понимания данных очень сложна, но часто нам удается свести ее к проблеме в категории векторных пространств. Линейная алгебра является предметом изучения этой категории.

В этом коротком курсе мы попытаемся понять векторные пространства и карты между векторными пространствами. Для тех, кто преобразует данные в векторы действительных чисел. . . поздравляю! Теперь вы находитесь в векторном пространстве и можете применить свое новое понимание.

Векторные пространства

Что такое векторное пространство? К сожалению, нельзя сказать, что такое векторное пространство — вы должны увидеть это сами. Шучу —

Пример 1. Давайте рассмотрим реальное двухмерное пространство R², которое во многих школах принято называть плоскостью x-y.

Набор R² — это прежде всего набор. То есть мы можем описать это как:

то есть набор всех пар действительных чисел. Но это больше, чем набор! Он также имеет двоичную операцию «+», определяемую как:

(p, q) + (r, s) = (p + r, q + s)

У этой бинарной операции есть несколько необычных свойств (которые она заимствовала из R).

1. Ассоциативность: (p + q) + r = p + (q + r)
2. Идентичность: существует элемент i, для каждого p которого есть i + p = p.
3. Инверсии: для каждого p существует элемент q такой, что p + q = q + p = i
4. Коммутативность: для каждого p и q мы имеем p + q = q + p

Набор со свойствами (1) и (2) называется моноидом. Набор со свойствами (1), (2) и (3) называется группой, а набор со всеми четырьмя свойствами называется абелевой группой.

Итак, R² также является моноидом, группой и абелевой группой при сложении. Но дело не только в этом! Также есть действие поля R на нашу абелеву группу R². Если v, w ∈ R² и a, b ∈ R ,, то мы обладают следующими свойствами:

1. 1v = v
2. (ab)v = a(bv)
3. (a + b)v = av + bv
4. a(v + w) = av + aw

В общем, когда объект S, действующий на абелеву группу, является просто кольцом, мы называем весь пакет S -модулем. В особом случае, когда S является полем (например, Q, R, или C), мы называем это векторным пространством.

Дополнительные примеры векторных пространств

Пример 2. Рассмотрим C как векторное пространство над R — это набор комплексных чисел a + bi, где a, b ∈ R рассматривается с действием R предоставлено:

c (a + bi) = ca + cbi

Пример 3: Рассмотрим набор R [x] многочленов от x с действительными коэффициентами.

Пример 4 (воспроизведение гильбертовых пространств ядра ♯): Рассмотрим функцию:

K: R² × R² → R определяется как (x, y) ↦ exp (- | x-y | ²)

где x, y — векторы в R², а |. | ² относятся к квадрату функции евклидова расстояния. задается по формуле: | (a, b) — (a ‘, b’) | ² = (a-a ‘) ² + (b-b’) ².

Эта функция является примером ядра (ядро — это симметричная положительно определенная функция). Для каждого x ∈ R² мы можем определить функцию:

k (x) (y): R² → R путем сопоставления y ↦ K (x, y)

Множество всех функций вида ∑α (i) k (x), где α ∈ R (после добавления некоторых точек техническим процесс, называемый завершением) — это очень специальное векторное пространство, называемое воспроизводящим ядерным гильбертовым пространством. Когда люди используют классификатор SVM (машина опорных векторов) в векторном пространстве V, они выбирают ядро ​​K, а затем решают проблему классификации в (обычно гораздо более крупном) ) ассоциированное воспроизводящее ядро ​​гильбертова пространства. Ядро, которое мы выбрали выше, известно как ядро ​​RBF.

Итак, сколько векторных пространств мы уже видели? Теперь у нас есть три (или четыре) примера «реальных векторных пространств» (иногда мы называем векторные пространства, которые имеют действие R, реальным векторным пространством) . Они все одинаковые? Что это хотя бы значит?! А вообще как сравнивать объекты в категории? !!

Здесь в игру вступают наши морфизмы — это инструменты, которые позволяют нам говорить такие вещи, как «эти два объекта одинаковы» или «этот объект помещается внутри другого объекта, поэтому он не больше». ” Так что же такое морфизм в категории векторных пространств?

Линейные преобразования

Морфизм в категории векторных пространств называется линейным преобразованием. Предположим, у нас есть два векторных пространства V и W над одним и тем же полем k с векторами v, v ‘∈ V и a ∈ k. Прежде всего, линейное преобразование — это функция из V в W в виде наборов: f: V → W. Однако, как мы уже упоминали, V и W — это больше, чем просто наборы! У них две операции. Чтобы f было линейным преобразованием, f должен соблюдать эти операции, что означает, что f удовлетворяет следующие два свойства:

1. f(v + v’) = f(v) + f(v’)
2. f(av) = a f(v)

Так же, как V и W имеют вложенные структуры (они представляют собой наборы, группы и векторные пространства над R), f — это морфизм множеств (мы называем его функцией), морфизм групп (мы называем его гомоморфизмом) и морфизм R векторные пространства (мы называем это линейным преобразованием).

Обычно в категории мы считаем два объекта V и W эквивалентными (обычно фраза изоморфна), когда есть морфизмы f: V → W и g: W → V, так что f ∘ g является тождеством на W и g ∘ f — это идентификатор на V.

Так . . . теперь мы можем задать вопрос: «Изоморфны ли R² и C (одно и то же)?» на который вы должны теперь ответить «Изоморфно как что ?!»

Примеры линейных преобразований

Пример 5: R² и C изоморфны как векторные пространства над R.

Пусть f: R² → C задается как (a, b) ↦ a + bi и пусть g: C → R² задается как a + bi ↦ (a, b). Убедитесь сами, что f ∘ g и g ∘ f являются картами идентичности на C и R² соответственно. Чтобы завершить доказательство изоморфизма, вам также необходимо убедиться, что эти функции линейны, то есть удовлетворяют двум указанным выше свойствам.

Пример 6: Рассмотрим линейное преобразование f из пространства многочленов степени ≤ 2 в пространство многочленов степени ≤ 1, заданное следующим образом:

a + bx +cx² ↦ a + bx

Можете ли вы убедить себя, что это линейно? Может ли f быть изоморфизмом?

Пример 7: Рассмотрим функцию f: R → R, заданную как a ↦ 2a + 1

Является ли эта функция линейным преобразованием?

Вам может показаться интересным, что определить, является ли функция линейным преобразованием, не так просто. . . ну, вроде как, но чтобы понять это, нам нужно ввести понятие основы.

Основа векторного пространства

А теперь давайте познакомимся с важной концепцией, известной как основа. Эта концепция поможет нам значительно упростить нашу модель того, как будут выглядеть векторные пространства и линейные преобразования. Мы обратимся к двум теоремам, которые мы не доказываем в этих заметках. Если вам не нравится принимать заявления без доказательств. . . отличный! Я призываю вас сначала попытаться доказать это самому.

Базис векторного пространства V — это набор векторов B = {v (1), v (2),. . . } ⊂ V такое, что для каждого u ∈ V существует единственный набор скаляров {α (1), α (2),. . . } такие, что

(примечание: более стандартным обозначением было бы иметь i в качестве подстрочного индекса к α и v, но я не знаю, как чтобы сделать это на Medium. Если вы это сделаете, дайте мне знать в комментариях!)

Обратите внимание, что это определение на самом деле имеет два свойства:

1. Существование представления для каждой точки u ∈ V
2. Уникальность этого представления.

Эти свойства часто полезно обсудить отдельно: если B имеет свойство (1), то мы говорим, что B охватывает V . В более общем смысле мы можем ссылаться на span (B) ⊆ V, набор всех векторов в V, которые можно записать как комбинацию векторов в B . Свойство (2) называется линейной независимостью — мы говорим, что B линейно независим от каждого вектора в промежутке B, который может быть однозначно представлен в терминах Б.

В этом смысле базис — это своего рода минимальный набор порождающих для вашего векторного пространства V. Теперь мы сформулируем два результата, которые мы захотим иметь под рукой:

Теорема 1. Каждое векторное пространство имеет базис.

Теорема 2. (Теорема размерности для векторных пространств) Если B и B ‘ являются базами V, то | B | = | B ’|. То есть B и B ’ имеют одинаковую мощность.

Второй результат позволяет нам дать определение, которое теперь имеет смысл:

Пусть V будет векторным пространством, а B — базисом. Мы называем | B | размер V.

Пример 8: Рассмотрим реальное векторное пространство R². Тогда мы можем увидеть, что:

• {(1, 0)} линейно независим, но не охватывает — это не основа.
• {(1, 0), (0, 1), (1, 1)} охватывает, но не является линейно независимым — это не основа.
• {(1, 0), (0, 1)} линейно независим и охватывает. . . это основа!

Пример 9: Каков размер R²?

Пример 10: Какова размерность C как реального векторного пространства? А как насчет комплексного векторного пространства (то есть векторного пространства над C)?

Решение линейных систем

Теперь мы переходим к вопросу, который периодически возникает в машинном обучении — решении линейных систем. Этот вопрос может показаться не связанным с нашим обсуждением основ, но мы скоро увидим связь.

Рассмотрим следующие уравнения:

Обычно это называется системой линейных уравнений. При каких условиях должно быть уникальное решение?

Это может показаться очень сложной задачей, но давайте запишем ее в других обозначениях:

Давайте перепишем это снова как

где a и b находятся в вещественных векторах размерности m-, а x — действительные числа .

Мы можем снова спросить, когда это уравнение должно иметь единственное решение? Что ж, по определению, если n = m и a составляют основу, тогда существует уникальное решение!

Пример 11: Когда нет решения вышеупомянутой проблемы? Когда существует бесконечно много решений?

Пример 12 (уравнения Беллмана для MDP ♯): Для тех, кто задается вопросом, где мы могли бы применить эти знания в машинном обучении — интересное приложение можно найти в рассмотрении Марковских процессов принятия решений или MDP. MDP состоит из набора состояний, в которых агент выбирает действия и получает вознаграждение. Политика π предписывает способ выбора действий с учетом состояния. Один вопрос, который возникает при изучении MDP, — это оценить ценность пребывания в данном состоянии s в рамках данной политики π —, определяемой как сумма полученных вознаграждений со скидкой. во времени в γ раз. Между этими значениями существует естественная рекурсивная связь, описываемая уравнением Беллмана:

где члены R (s, π (s)), γ и P (s ’| s, π (s)) — все константы, которые можно оценить. Вы заметите, что если имеется n общих состояний, то существует n подобных отношений — линейных в терминах V (s) ( из которых также есть n). Таким образом, пока существует линейная независимость между отношениями — существует уникальное решение для системы, и мы можем определять значения каждого состояния!

Линейные преобразования в свете основы

Определение линейного преобразования

Теперь ограничимся случаем векторных пространств с конечным базисом — так называемых конечномерных векторных пространств. Теперь мы готовы сделать критическое наблюдение:

Линейное преобразование определяется тем, что оно делает с базисом.

То есть, предположим, что V — вещественное векторное пространство с базисом {v (1), v (2),. . . , v (n)}. Допустим, мы хотим построить линейное преобразование L: V → W, где W — какое-то другое векторное пространство. Каким должно быть L (v) для данного v ∈ V?

Что ж, мы знаем, что v = a (1) v (1) + a (2) v (2) +. . . + a (n) v (n) для некоторых действительных чисел a (i). По свойствам линейных преобразований:

L(v) = a(1)L(v(1)) + a(2)L(v(2)) + . . . + a(n)L(v(n))

Итак, поскольку любой элемент V может быть записан в терминах v (i) (наш базис), мы видим, что задание линейного преобразования V → W эквивалентно выбору n векторов в W — то есть выбору L (v (1)),. . . , L (v (n)) ∈ W.

Пример 13 (Классификационная теорема для конечномерных векторных пространств): Докажите себе, что все векторные пространства над полем k размерности n изоморфны.

Ранг и аннулирование

Мы также увидели, насколько мощной может быть концепция размерности при описании векторных пространств. Фактически, мы доказали, что в конечномерном случае размерность характеризует класс изоморфизма! Теперь мы хотели бы использовать этот язык также для описания линейных преобразований.

Пусть L: V → W — линейное преобразование. Пусть {v (1), v (2),. . . , v (n)} быть основой V. Рассмотрим диапазон множества {L (v (1)), L (v (2)),. . . , L (v (n))} (мы определили промежуток набора векторов выше в базах раздела). Это само векторное пространство, записанное L (V) и часто называемое изображением L. Поскольку L (V) — векторное пространство, оно имеет размерность, мы называем это число (размерностью) рангом L.

Точно так же мы можем рассмотреть набор векторов в V, которые отправляются в нулевой вектор (вектор всех нулей) в L. Мы называем этот набор ядром L, записывается как ker (L) (и отличается от функции ядра, упомянутой в примере воспроизведения ядра Hilbert пробелы!). Однако, как мы увидим в следующем упражнении, ker (L) — это больше, чем просто набор!

Упражнение 14: Докажите себе, что ker (L) = {v ∈ V | L (v) = 0} — векторное пространство.

Поскольку ker (L) — векторное пространство, мы можем спросить его размерность. Мы называем это число недействительностью L. Теперь мы сформулируем (без доказательства) так называемую теорему «ранг-нуль», которая регулирует отношения между dim (V), rank (L), и недействительностью. (L).

Теорема (нулевой ранг): Пусть L: V → W — линейное преобразование, где V конечномерно. Потом:

dim (V) = ранг (L) + недействительность (L)

или сказал иначе:

dim (V) = dim (L (V)) + dim (ker (L))

Если вы исходите из точки зрения данных — думайте о точках в векторном пространстве как о данных. Тогда за теоремой о нулевом ранге стоит хорошая интуиция. При линейном преобразовании данных вы начинаете с определенного количества информации, представленной dim (V). Количество информации, имеющейся у вас после преобразования (ранг (L)), равно количеству информации, с которой вы начали (dim (V)) минус количество информации, потерянной преобразованием (nullity (L)).

Упражнение 15: Пусть L: V → V — линейное преобразование. Обратным L является карта J такая, что L ∘ J и J ∘ L идентичны на V. Учитывая L, когда существует J? (Подсказка: существует только в том случае, если nullity (L) является специальным значением)

Координаты

До сих пор мы писали вещи в общем. Обычно, когда люди говорят о векторных пространствах, они пишут кортежи, например (1, 3, 0, 0, 7) и матрицы, например

Так что здесь происходит? Что ж, для конечномерных векторных пространств (помните, что для данного поля и данной размерности есть только одно!) Есть естественный выбор базиса — стандартный базис. Для R⁴ стандартная основа выглядит так:

{(1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0), (0, 0, 0, 1)}

которые мы бы сократили: {e (1), e (2), e (3), e (4)}.

Затем мы используем сокращение (7, 2, 1, 4) для обозначения 7e (1) + 2e (2) + 1e (3) + 4e (4). А как же матрица. . . что такое матрица?

Матрица — это способ кодирования информации линейного преобразования. Предположим, у нас есть линейное преобразование L: R³ → R⁴. Мы сказали, что это эквивалентно выбору 3 векторов в R⁴: L (e (1)), L (e (2)) и L (e (3)).

Скажите, что эти векторы приведены ниже:

• L(e(1)) = (1, 0, 7, 3)
• L(e(2)) = (0, 4, 4, 4)
• L(e(3)) = (2, 1, 3, 9)

Затем матрица этих вариантов в виде векторов-столбцов дает нам преобразование посредством умножения матриц:

Таким образом, мы легко можем увидеть структуру преобразования.

Пример 16: Убедитесь, что умножение матриц линейное. Например, если v = a (1) v (1) +. . . + a (n) v (n), тогда Mv = a (1) Mv (1) +. . . + a (n) Mv (n).

Пример 17. Рассмотрим линейное преобразование L, задаваемое следующим образом:

• Куда и откуда идет L (какой домен и кодомен)?
• Каков размер ker (L)?
• Каков размер изображения?
• Может ли L иметь обратное?

Линейная регрессия

Модель линейной регрессии M: V → R — это аффинное преобразование. То есть он имеет форму x ↦ Lx + b, где L — линейное преобразование, а b — вектор в целевом пространстве. (или codomain) — здесь просто реальный номер.

Пример 18: Какую форму имеет L? Согласуйте это определение с характеристикой линейной регрессии как функции вида f (x (1), …, x (n)) = β (0) + ∑ β (i) x (i) .

В качестве альтернативы мы можем расширить V на одно измерение до V ‘ и определить линейную регрессию как линейное преобразование V’ → R с пониманием того, что мы будем передавать только значения вида (1, x (1), x (2), …, x (n)).

Если D ⊂ V ‘ (наши данные) представляет собой набор точек в векторном пространстве нашей предметной области (обычно называемом пространством признаков), естественно подумать о D как матрица X, где каждая строка является строкой данных. Если y является вектором (столбцом) меток для каждой строки X, то так называемый «обычный метод наименьших квадратов» дает нам желаемое линейное преобразование, задаваемое следующим образом:

Пример 19: Что должно быть правдой, чтобы это преобразование существовало? Какое исправление мы можем использовать, если вышеупомянутое преобразование не существует?

Чтобы получить представление о приведенном выше примере, рассмотрим следующий код R:

X <- as.data.frame(matrix(
                  c(0.0, 0.5, 1.0, 0.0, 0.0,
                    0.0, 1.0, 2.0, 0.0, 0.0,
                    0.7, 2.0, 1.0, 1.0, 1.0,
                    7.0, 9.0, 3.0, 2.0, 6.0),
                  ncol = 4,
                  nrow = 5))
# This defines the following matrix:
# > X
#   V1  V2  V3 V4
# 1 0.0  0 0.7  7
# 2 0.5  1 2.0  9
# 3 1.0  2 1.0  3
# 4 0.0  0 1.0  2
# 5 0.0  0 1.0  6
linearModel <- lm(V4 ~ V1 + V2 + V3, data=X)

Этот код определяет матрицу данных и соответствует модели линейной регрессии, используя первые 3 столбца для моделирования последнего столбца. Если вы осмотрите подходящую модель:

linearModel
# Which defines this model:
# 
# Call:
# lm(formula = V4 ~ V1 + V2 + V3, data = X)
# Coefficients:
# (Intercept)           V1           V2           V3  
#       1.744       -2.114           NA        3.763

Мы видим, что из модели убрана одна из функций! Вы можете объяснить, почему это было сделано?

Собственные векторы и собственные значения

Учитывая линейное преобразование L: V → V,, мы можем задать следующий интересный вопрос: «Существуют ли какие-либо векторы v ∈ V, чтобы L просто масштабировал их (т.е. длиннее или короче без изменения направления)? » Этот вопрос имеет смысл, потому что L переводит V в V. Вектор v, удовлетворяющий этому условию, называется собственным вектором, а соответствующее значение λ называется собственным значением.

Более конкретно, допустим, что L: R² → R² со стандартными основаниями, так что мы можем записать его в виде матрицы M. Тогда возникает вопрос: существует ли вектор v ∈ R² и действительное число λ ∈ R, так что Mv = λv?

Если мы позволим I быть единичной матрицей (то есть преобразованием, переводящим каждый вектор в себя), то это эквивалентно запросу, есть ли решения уравнения (M-λI) v = 0

Итак, мы свели вопрос о том, существуют ли v и λ, до вопроса о том, имеет ли M-λI нетривиальное ядро. Что ж, у нас уже есть все необходимое, чтобы ответить на этот вопрос, но оказывается, что есть хороший числовой трюк, который мы можем использовать, который называется определителем. Определитель квадратной матрицы n × n M является полиномом степени n от элементов M. Легко записать в футляре 2 × 2. Позволять

Тогда определитель det (M) определяется как det (M) = ad-bc. В любом случае для нас актуальным является следующее:

Теорема: квадратная матрица M имеет обратную тогда и только тогда, когда det (M) ≠ 0.

Напомним, что наличие инверсии — это то же самое, что наличие тривиального ядра, поэтому, если мы хотим знать, когда M-λI имеет ядро, мы должны просто искать, когда det (M-λI ) = 0. Это просто поиск нулей полинома степени n!

Вернемся к нашему примеру 2 × 2. Мы убедились, что λ ∈ R является собственным значением M тогда и только тогда, когда det (M — λI) = 0 . То есть, когда:

который мы можем расширить до λ²- (a + d) λ + (ad-bc) = 0.

Есть ли нули у полинома степени 2? Иногда нет, иногда один, иногда два. Предположим, есть собственное значение для M, назовем его λ ’, как мы можем найти связанный собственный вектор?

Что ж, это сводится к нахождению векторов v = (v (1), v (2)) в ядре M-λ’I, что составляет решение для v:

Умножение матрицы на вектор сводится к поиску решения линейной системы:

Пример 20. Покажите, что матрица:

не имеет собственных значений. (Примечание: это очевидно геометрически)

Пример 21. Покажите, что матрица

имеет одно собственное значение. Можете ли вы найти соответствующий собственный вектор?

Пример 22. Покажите, что матрица

имеет два различных собственных значения. Можете ли вы найти соответствующие собственные векторы?

Оказывается, наличие в указанной матрице базиса из собственных векторов не случайно. Фактически, это следствие следующей теоремы:

Теорема (вещественная спектральная теорема): Пусть M — вещественная симметричная матрица размером n × n (то есть t (M) = M, где t (M) обозначает транспонирование M). Тогда область этого преобразования имеет базис из собственных векторов.

Эта теорема на самом деле довольно часто используется в науке о данных через так называемую матрицу ковариации дисперсии:

Пример 23 (анализ основных компонентов ♯): даны центрированные и масштабированные данные X (центрирование означает, что среднее значение выборки для каждого столбца равен нулю, а масштабирование означает, что выборочная дисперсия для каждого столбца равна 1), матрица дисперсии-ковариации задается как (1 / (m-1)) Xt (X). Основными компонентами данных являются собственные векторы {p (1), p (2),. . . , p (n)} этого преобразования.

У этих собственных векторов есть несколько интересных свойств:

1. У них есть основа, и они ортогональны (по действительной спектральной теореме).
2. Они некоррелированы (вы можете проверить это простым вычислением!)
3. Величина соответствующего собственного вектора говорит нам, какая часть общей дисперсии данных объясняется этой особенностью.

В результате этих свойств люди часто меняют исходное пространство признаков на пространство, охватываемое первыми k (упорядоченными по величине связанных собственных значений) собственными векторами ковариационной матрицы (то есть первыми k основных компонентов). Это пространство более низкой размерности, которое по-прежнему содержит максимальное количество дисперсии, содержащейся в данных.

Выводы

Очень часто в науке о данных — после всей тяжелой работы по сбору бизнес-требований, упорядочиванию доступа к данным, запросам, очистке и числовому кодированию данных — мы оказываемся в привилегированном положении, когда нам нужно рассуждать о точках в векторном пространстве (или функции). Космос). Модели классификации и регрессии (среди других основных продуктов мира науки о данных) располагаются на вершине этих векторных пространств, и их поведение в значительной степени определяется геометрией этого пространства.

Теперь мы строго понимаем свойства пространства, подобные измерению, а также поведение структурных (линейных) преобразований. Мы понимаем, как эти преобразования сохраняют и теряют информацию, и мы видели множество применений этих принципов.

Я надеюсь, что этот базовый фрейм может значительно упростить ваше понимание многих методов машинного обучения, таких как SVM, MDP, PCA или любой другой цепочки букв, которую вы, возможно, захотите изучить. Если есть тема, которая, по вашему мнению, должна была быть включена в эти заметки, дайте мне знать ниже!

Линейное подпространство является линейным пространством относительно операций объемлющего линейного пространства и поэтому имеет размерность и базис.

Теорема 2.4. Если H — линейное подпространство линейного пространства L, то dimH ≤ dimL. Если к тому же H ≠ L, то dimH < dimL.

◄ Любой базис линейного подпространства H, рассматриваемого как линейное пространство, является линейно независимой системой векторов в объемлющем линейном пространстве L. Если этот базис из Н является базисом и в L, то, согласно теореме 1.5, dimH = dimL и ясно, что в этом случае H = L, так как у них есть общий базис. Если базис из Н не является базисом объемлющего линейного пространства L, то существует такой вектор x ∈L, который не является линейной комбинацией векторов этого базиса. В этом случае, конечно, линейное подпространство H не может совпадать с L. Добавив вектор х к векторам базиса, получим линейно независимую систему векторов (см. свойство 4°, с. 27). Это значит, что в L найдено больше линейно независимых векторов, чем dimH. Следовательно, согласно определению 1.5 размерности линейного пространства, dimН < dimL. ►

Замечание 2.1. Любой базис собственного подпространства Н линейного пространства L можно расширить, добавив вектор так, что расширенная система векторов останется линейно независимой. Если расширенная система опять не является базисом в L, процедуру расширения можно повторить. Для конечномерного линейного пространства очередное расширение через какое-то количество шагов станет невозможным, так как количество векторов в линейно независимой системе не может превышать размерности линейного пространства. Максимально расширенная система векторов будет линейно независимой, а любой вектор будет представляться ее линейной комбинацией, т.е. эта система векторов будет базисом в L. Согласно теореме 1.5, количество векторов в этой системе будет равно размерности линейного пространства L.

Приведенное рассуждение показывает, что любой базис собственного линейного подпространства может быть расширен до базиса объемлющего линейного пространства добавлением новых векторов. Например, рассмотрим линейное пространство V₃ с ортонормированным базисом i, j, k. Линейное подпространство Н = span{i,j} имеет размерность 2, так как его базисом является пара векторов i, j. Действительно, они линейно независимы, а любой вектор из Н представляется в виде линейной комбинации i и j согласно определению этого подпространства. Этот базис можно расширить до базиса в V₃, добавив один вектор. В качестве этого, дополнительного вектора можно взять любой вида x = αi + βj + γk с γ ≠ 0.

Теорема 2.5. Если H₁ и Н₂ — линейные подпространства линейного пространства L, то

dim(H₁ + Н₂) = dimH₁ + dimН₂ — dim(Н₁ ∩ Н₂).

◄ В линейном подпространстве Н₁ ∩ Н₂ выберем некоторый базис е = (e₁ … e_m). Множество Н₁ ∩ Н₂ является линейным подпространством не только в L, но и в его части H₁. Поэтому выбранный базис можно дополнить некоторой системой векторов f = (f₁ … f_l) до базиса (е f) в линейном подпространстве H₁. Точно так же систему е можно дополнить некоторым набором векторов g = (g₁ … g_k) до базиса (е g) в Н₂. Докажем, что система векторов

(е f g) = (е₁ … е_m f₁ … f_l g₁ … g_k)

является базисом в линейном пространстве Н₁ + Н₂.

Во-первых, установим, что указанная система линейно не-зависима. Пусть имеет место равенство

α₁e₁ +… + α_me_m + β₁f₁ + …+ β₁f₁ + γ₁g₁ + … + γ_kg_k = 0. (2.4)

Тогда для вектора

y = β₁f₁ + … + β_lf_l (2.5)

выполнено равенство

у = -α₁e₁ — … — α_mе_m — γ₁g₁ — … — γ_kg_k. (2.6)

Согласно равенству (2.5) заключаем, что у ∈ H₁, а согласно (2.6) делаем вывод, что у ∈ H₂. Следовательно, у ∈ Н₁ ∩ Н₂ и потому имеет единственное разложение

y = δ₁e₁ +…+ δ_me_m (2.7)

по базису е линейного пространства Н₁ ∩ Н₂.

Разложение (2.7) можно рассматривать как разложение по базису (е g) в линейном подпространстве H₂. Но тогда разложения (2.6) и (2.7) совпадают как разложения одного и того же вектора в базисе (е j). Следовательно, γ_j = 0, j = 1,k, а все коэффициенты δ_i, отличаются от соответствующих коэффициентов α_i лишь знаком. С другой стороны, представление (2.5) вектора у и представление (2.7) того же вектора являются разложениями одного вектора в базисе (е f) линейного подпространства H₁ и потому совпадают. Их совпадениё означает, что β = … = β_l = 0 и δ₁ = … = β_m = 0. Тогда и α₁ =
= … = α_m = 0. Таким образом, все коэффициенты произвольно взятой линейной комбинации (2.4), равной нулевому вектору, оказались равными нулю. Значит, система векторов (е f g) линейно независима.

Во-вторых, любой вектор у ∈ H₁ + Н₂ есть линейная комбинация системы векторов (е f g). Действительно, такой вектор представим в виде у = y₁ + у₂, где y₁ ∈ H₁, у₂ ∈ H₂. Вектор y₁ представляется линейной комбинацией системы векторов (е f), а у₂ — линейной комбинацией системы векторов (е g). Поэтому у разлагается по системе векторов (е f g).

Итак, система векторов (е f g) линейно независима и любой вектор из H₁ + H₂ разлагается по этой системе. Следовательно, (е f g) — базис в H₁ + H₂. Нам остается подсчитать размерности:

Таким образом, получаем утверждение теоремы. ►

Следствие. dim(H₁ ⊕ H₂) = dimH₁ + dimH₂.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ