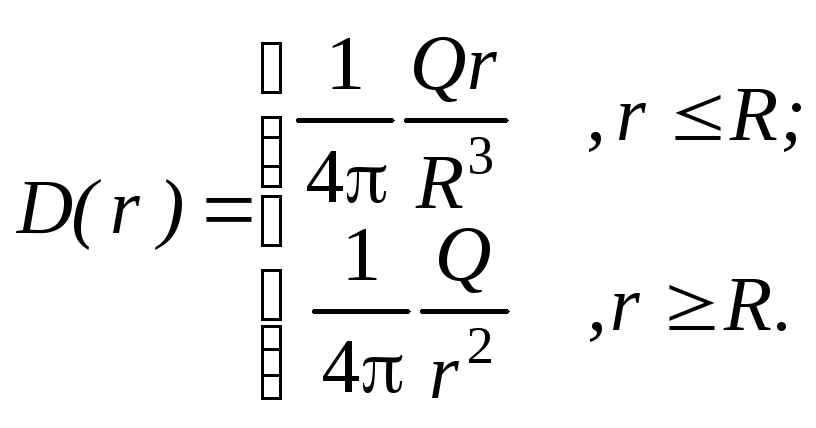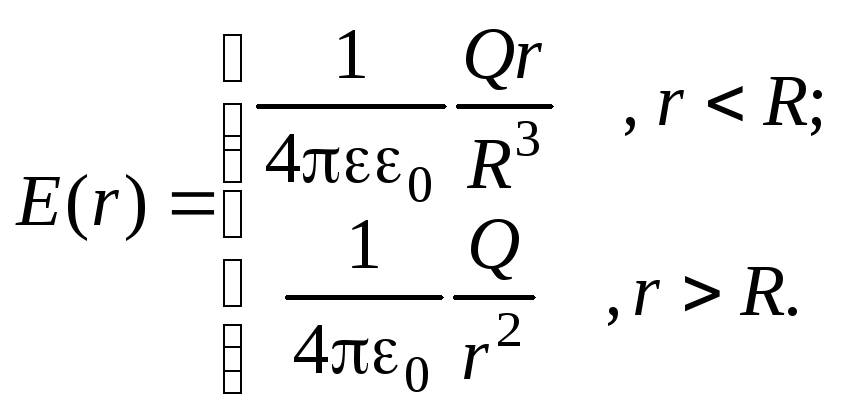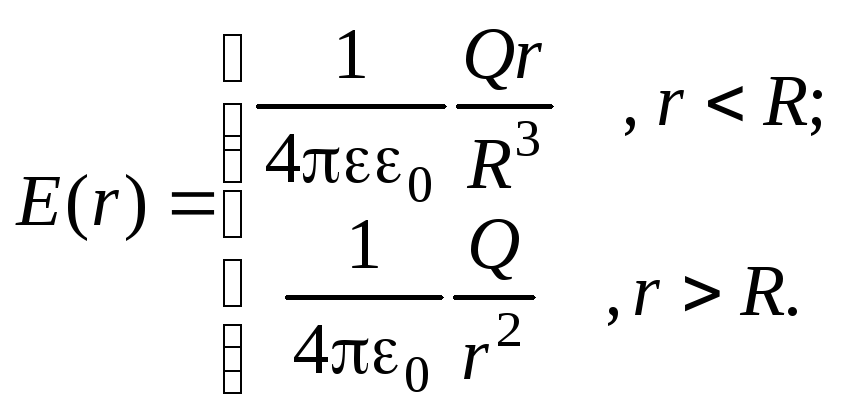Влияние диэлектриков на электрическое поле сводится к ответному действию возникающих в поле поляризационных зарядов. Теорема Остроградского-Гауса для тел в вакууме электростатического поля может быть трансформирована с помощью добавления к свободным зарядам поляризационных для получения теоремы с диэлектриками. В этом случае она запишется как:
Со значением qjsυ в качестве связанных зарядов, qi — свободных зарядов, ΦE — потока вектора напряженности электрического поля.
Теорема Остроградского-Гаусса
Если использовать вектор электрического смещения D→, то это заметно облегчает анализ поля при наличии диэлектрика. Теорему Остроградского-Гаусса при наличии диэлектрика можно записать в интегральном виде:
∮SD→·dS→=∑i=1Nqi=Q, где Q является суммарным свободным зарядом, находящийся внутри объема, который ограничен поверхностью S.
Поток вектора D→ через замкнутую поверхность может быть определен только с помощью свободных зарядов. В вакууме векторы D→ и E→ совпадающие.
Дифференциальная форма теоремы Гаусса выражения ∮SD→·dS→=∑i=1Nqi=Q изображается как:
div D→=ρ с ρ, являющейся объемной плотностью свободных зарядов.
Теорема Остроградского-Гаусса вида ∮SD→·dS→=∑i=1Nqi=Q и div D→=ρ справедлива только в электростатике и выполняется для переменных полей. Ее относят к составной части системы уравнений Максвелла.
Теорема Остроградского-Гаусса в дифференциальной форме
Напомним формулу вектора электрической индукции:
D→=ε0E→+P→ со значением ε0 в качестве электрической постоянной, E→ — вектора напряженности, P→ — вектора поляризации.
Произведем подстановку формулы D→=ε0E→+P→ в div D→=ρ:
div D→=div ε0E→+P→=ε0div E→+div P→.
При использовании теоремы Остроградского-Гаусса дифференциального вида, получим:
div E→=1ε0ρ-div P→.
Для вектора напряженности вышеуказанная формула примет вид в присутствии диэлектрика:
div E→=1ε0ρ+ρsv с ρsv, являющейся плотностью заряда. В этом случае необходимо применить div E→=1ε0ρ+ρsv и div E→=1ε0ρ-div P→:
div P→=-1ε0csv.
Теорема Остроградского-Гаусса для диэлектриков
Теорема Остроградского-Гаусса для вектора электрического смещения в диэлектрике выглядит также, как и для напряженности поля в вакууме. Отсюда следует, что математические соотношения, получившиеся для E→ поля в вакууме, аналогичны записям для однородного диэлектрика при замене напряженности электрического поля на вектор D→.
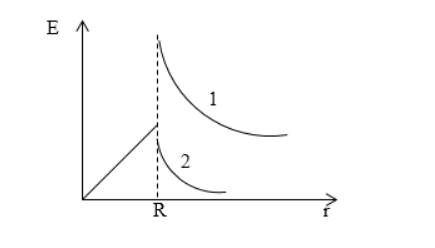
Дан диэлектрический шар, имеющий диэлектрическую проницаемость ε1, равномерно заряжен по объему с постоянной плотностью заряда ρ. Его нахождение в среде обусловлено наличием диэлектрической проницаемости ε2. Изобразить график напряженности поля шара от расстояния до его центра.
Решение
Поле, создаваемое шаром по заданным условиям, имеет сферическую симметрию. Необходимо рассмотреть его внутри шара r≤R. Для нахождения E(r) выбирается сферическая поверхность с радиусом меньше сферы. По теореме Остроградского-Гаусса:
E·S=qε1ε0, где S — площадь поверхности сферы, которая была выделена. Отсюда следует:
S=4πr2.
Заряд, находящийся внутри сферы, ищем из формулы:
q=ρV=ρ43πr3.
Очевидно, что будут происходить изменения напряженности поля внутри шара r≤R, согласно выражениям:
E·4πr2=ρ43πr3ε1ε0,
E=ρr3ε1ε0.
Перейдем к рассмотрению поля вне шара r≥R. Для нахождения E(r) выбираем сферическую поверхность с радиусом больше радиуса сферы. По теореме Остроградского-Гаусса получим:
E·S=qε2ε0, где S обозначает площадь поверхности выделенной сферы. Отсюда следует:
S=4πr2.
Формула S=4πr2 имеет r≥R. Поэтому находящийся внутри заряд выделенной сферы находится из:
q=ρV=ρ43πR3.
Далее следует подставить площадь из S=4πr2, заряд из q=ρV=ρ43πR3, подставив в E·S=qε2ε0:
E·4πr2=ρ43πR3ε2ε0.
E=ρR33ε2ε0r2.
В результате запишем:
E=ρr3ε1ε0 при r≤R,E=ρR33ε2ε0r2 при r≥R.
Рисунок 1
Ответ: графики показаны на рисунке 1. Внутри шара напряженность увеличивается прямо пропорционально расстоянию от центра шара. Вне шара она равняется E~1r2. На границе диэлектриков происходит разрыв. Кривая под номером 1 соответствует условию ε1>ε2.
Предположим, что имеется воображаемая сфера, в центре которой находится точечный заряд. Будет ли изменяться поток вектора напряженности через эту поверхность, если: 1) все пространство будет заполнено однородным и изотопным диэлектриком, 2) произвести замену сферической поверхности на кубическую?
Решение
- По теореме Остроградского-Гаусса поток вектора напряженности через поверхность сферы в пространстве с диэлектриком будет равняться:
ΦE=∮SE→dS→=1ε0q+∑j=1Kqjsv, со значением qjsv в качестве связанных зарядов, которые вызваны поляризацией диэлектрика полем одиночного заряда, q в качестве свободного заряда, находящегося в центре сферы.
Учитывая теорему Остроградского-Гаусса, формула потока вектора напряженности через поверхность сферы в пространстве без диэлектрика примет вид:
ΦE=∮SE→dS→=1ε0q.
- Поле было создано при помощи точечного свободного заряда, то при замене формы поверхности потока вектор напряженности не будет изменяться, потому как равняется аналогичным значению заряда, находящегося на поверхности.
Ответ:
- изменится,
- не изменится.
Электрическое
поле в диэлектрической среде создается
как свободными, так и связанными зарядами.
Вектор напряженности
характеризует результирующее поле.
Согласно принципу суперпозиции (1.9),
напряженность поля в веществе равна
геометрической сумме напряженностей
полей свободных и связанных зарядов:
.
Теорема
Остроградского–Гаусса (1.26) может быть
применена в диэлектрической среде, если
в правой части равенства рассматривать
алгебраическую сумму всех свободных и
связанных зарядов, охватываемых гауссовой
поверхностью:
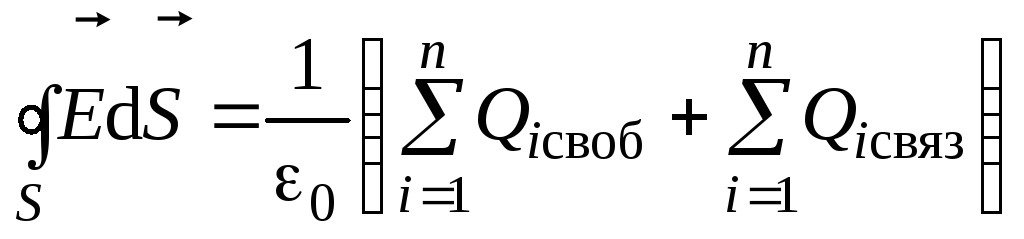
Использование
полученного соотношения для расчета
напряженности поля, создаваемого
заданной системой свободных зарядов в
диэлектрической среде, осложняется
тем, что заранее не известно распределение
связанных зарядов в поле. Соответственно,
невозможно определить величину связанного
заряда, попавшего внутрь гауссовой
поверхности. Поскольку молекулы
диэлектрика электрически нейтральны,
то вклад в
дадут только те молекулы, диполи которых
“перерезаются” гауссовой поверхностью.
Чтобы определить их число, рассмотрим
поляризованный диэлектрик, диполи
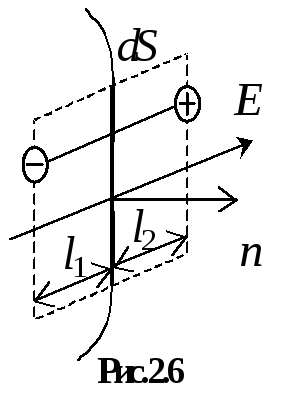
которого ориентированы по направлению(рис.2.6). На рисунке указан фрагмент
гауссовой поверхности площадью,
внешняя нормаль к немуи “перерезанный” молекулярный диполь
с плечом.
Ориентация диполей приводит к тому, что
часть молекулярных зарядов при повороте
диполей выходит за пределы гауссовой
поверхности, а часть зарядов входит
внутрь нее. Покидают объем, ограниченный
гауссовой поверхностью, положительные
заряды, а входят в него отрицательные.
Выделим
некоторый объем диэлектрика в виде
косого цилиндра, образующая которого
параллельна
.
Гауссова поверхность разбивает объем
цилиндра на две части. На рис. 2.6 слева
от,
т.е. внутри гауссовой поверхности,
располагается часть выделенного объема
диэлектрика с образующей длиной.
Общее число положительных зарядов,
покинувших этот объем диэлектрика,
равно,
гдеп
– концентрация молекул диэлектрика.
Справа от
,
т.е. вне гауссовой поверхности,
располагается часть выделенного объема
диэлектрика с образующей длиной.
Общее число отрицательных зарядов,
покинувших этот объем диэлектрика и
вошедших внутрь гауссовой поверхности,
равно.
Поскольку отрицательный и положительный
заряды молекулярных диполей равны по
модулю (),
то можно определить модули “вышедших”
и “вошедших” зарядов:,
.
Однако, увеличение отрицательного
связанного заряда, находящегося внутри
гауссовой поверхности, наэквивалентно уменьшению положительного
связанного заряда, находящегося внутри
гауссовой поверхности на такую же
величину. Таким образом, при поляризации
диэлектрика число положительных
связанных зарядов, находящихся вблизи
участка гауссовой поверхности площадью,
уменьшается на.
Учтем, что,
а.
Тогда.
В целом из объема, ограниченного гауссовой
поверхностью, уходит электрический
заряд
.
С
учетом полученного соотношения
преобразуем выражение (1.26) теоремы
Остроградского–Гаусса так:
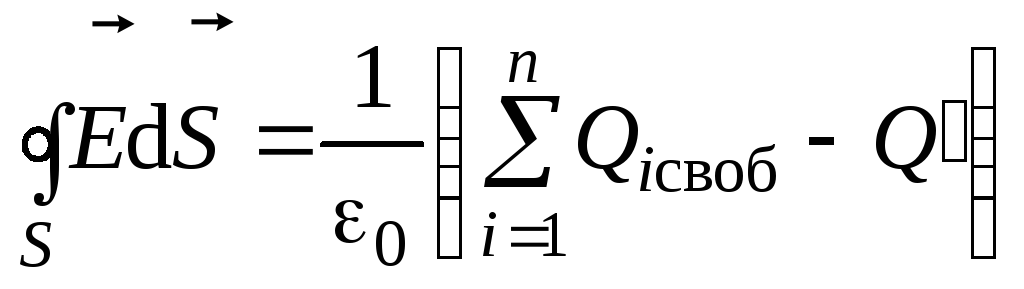
,
.
Согласно
(2.11) последнее равенство запишем в виде
.
(2.15)
Именно
в таком виде теорему
Остроградского–Гаусса
удобно применять в
диэлектрических средах:
поток
вектора электрического
смещения
через произвольную замкнутую поверхность
равен алгебраической сумме свободных
зарядов, охваченных этой поверхностью.
При
расчете напряженности электростатического
поля в диэлектрической среде необходимо
сначала определить модуль и направление
вектора электрического смещения
.
Затем, пользуясь соотношением (2.11)
необходимо определять величину.
Рассмотрим пример 1 из п.1.7 и определим
напряженность электростатического
поля во всех точках пространства, если
электрический заряд
равномерно распределен по объему
диэлектрического шара радиусом R,
относительная диэлектрическая
проницаемость которого равна .
Повторяя
рассуждения п.1.7, получим
Так
как
,
то
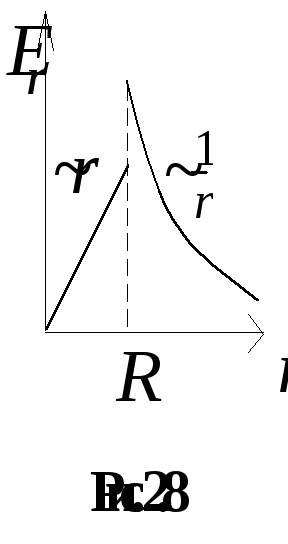
Графики
полученных зависимостей приведены на
рис. 2.7 и 2.8. Отметим, что зависимость
имеет разрыв на границе шара (при
),
т.к. на поверхности шара находится
связанный положительный заряд.
Рассмотрим
физический смысл относительной
диэлектрической проницаемости .
Пусть в вакууме (при отсутствии
диэлектрика) совокупность свободных
зарядов создает электрическое поле,
характеризующееся вектором
.
В диэлектрике те же свободные заряды
создадут поле, для которого.
В соответствии с (2.15),.
Поэтому
.
(2.16)
Поскольку
,то
относительная диэлектрическая
проницаемость показывает, во сколько
раз напряженность поля в вакууме больше,
чем напряженность поля в диэлектрике.
Таким образом, диэлектрик обладает
способностью ослаблять электрическое
поле.
Так
как
,
то
Графики
полученных зависимостей приведены на
рис. 2.7 и 2.8. Отметим, что зависимость
имеет разрыв на границе шара (при
),
т.к. на поверхности шара находится
связанный положительный заряд.
Рассмотрим
физический смысл относительной
диэлектрической проницаемости .
Пусть в вакууме (при отсутствии
диэлектрика) совокупность свободных
зарядов создает электрическое поле,
характеризующееся вектором
.
В диэлектрике те же свободные заряды
создадут поле, для которого.
В соответствии с (2.15),.
Поэтому
.
(2.16)
Поскольку
,
то относительная диэлектрическая
проницаемость показывает, во сколько
раз напряженность поля в вакууме больше,
чем напряженность поля в диэлектрике.
Таким образом, диэлектрик обладает
способностью ослаблять электрическое
поле.
Соседние файлы в папке Шпоргалки
- #
- #
- #
- #
- #
- #
- #
Теорема Остроградского-Гаусса: история открытия
Теорема Остроградского-Гаусса или теорема о дивергенции — один из основополагающих законов электродинамики, устанавливающий связь между электрическими зарядами и электрическим полем.
Эта теорема выражает равенство между потоком напряженности электрического поля через замкнутую поверхность и значением заряда (q), расположенного внутри объема этой поверхности.
В отличие от закона Кулона теорема Остроградского-Гаусса позволяет выразить свойства электростатического поля в более общей форме.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Имея заряд (q), окруженный замкнутой поверхностью любой формы, в каждой точке этой поверхности можно наблюдать электрическое поле, спровоцированное этим зарядом. Чтобы найти поток напряженности электрического поля, необходимо перемножить напряженность этого поля и сколь угодно малую единицу окружающей заряд поверхности. А после, зная это, можно рассчитать поток напряженности, который проходится на каждую единицу поверхности.
В этом заключается суть теоремы Остроградского-Гаусса. Ее можно сформулировать как совокупный поток напряженного электрического поля, проходящий через плоскость, окружающую заряд, пропорционален величине заряда.
Теорема активно используется в электродинамике, а для более сложных полевых теорий, существуют ее обобщения и аналоги.
Теорема была выведена двумя учеными независимо друг от друга. Российский математик Михаил Остроградский в 1828 году вывел теорему, применимую для векторного поля любой природы, а то время как его немецкий коллега Карл Гаусс, увлекшись изучением магнетизма и электрических полей, представил миру свою теорему применительно к электростатическому полю.
Михаил Остроградский доказал теорему электростатики через уравнение дифференциальной формы, в то время как Карл Гаусс в 1839 году получил аналогичный результат в интегральной форме.
Физический смысл формулы
Физический смысл формулы сводится к тому, что поток электрической индукции ((D)) через любую замкнутую поверхность (S) пропорционален суммарному заряду, заключенному внутри этой поверхности ((q)).
Вывод формулы в интегральной форме
Начнем с того, что поток вектора напряженности электрического поля равен числу линий напряженности, пересекающих поверхность (S). Обратим внимание на рисунок 1. В данном случае поток вектора напряженности через (dS) будет равен:
(dphi_E=EdScosleft(alpharight)=E_ndS)
Таким образом, в однородном поле (phi_E=ES) , а в произвольном электрическом поле:
(phi_E=int_SE_ndS=int_soverrightarrow Edoverrightarrow S)
В этом случае (doverrightarrow S=dSoverrightarrow n) — положение (dS) в пространстве задается с помощью вектора (overrightarrow n). То есть направление вектора (doverrightarrow S) совпадает с направлением (overrightarrow n) .
Теперь попробуем вычислить поток вектора (overrightarrow E) через произвольную замкнутую поверхность (S), которая окружает заряд (q) (рисунок 2). Окружим заряд (q) сферой (S_1). Центр сферы и центр заряда совпадают, поэтому радиус сферы (S_1) равен (R_1).
Проекция (overrightarrow E) на направление внешней нормали одинакова на каждой точке поверхности (S_1) и вычисляется по формуле:
(E_n=frac1{4pivarepsilon_0}frac q{R_1^2})
В таким случае поток через (S_1) можно узнать, применив формулу:
(phi_E=oint_{S_1}E_ndS=frac q{4pivarepsilon_0}4pi R_1^2=frac q{varepsilon_0})
Пример
Далее вычислим поток через сферу (S_2), которая имеет радиус (R_2) по формуле:
(phi_E=oint_{S_2}frac q{4pivarepsilon_0R_2^2}dS=frac q{4pivarepsilon_0R_2^2}4mathrmpi{mathrm R}_2^2=frac q{varepsilon_0})
Учитывая непрерывность линии (overrightarrow E), поток через любую поверхность (S) будет равен той же величине:
(phi_E=oint_SE_ndS=frac q{varepsilon_0})
Формула для нескольких зарядов будет записываться следующим образом:
( phi_E=oint_SE_ndS=frac{sum_{}q}{varepsilon_0})
Вывод формулы в дифференциальной форме
Дифференциальная форма теоремы используется для расчета электростатического поля в случае произвольного пространственного распределения зарядов. В этой форме отражена связь между объемной плотностью заряда (rho) и изменением (overrightarrow E) вокруг этой точки пространства.
Используем теорему Остроградского-Гаусса, в соответствии с которой поток вектора (overrightarrow A) через любую замкнутую поверхность равняется интегралу от его дивергенции по объему, охваченному этой поверхностью:
(oint_SA_ndS=int_Vdivoverrightarrow AdV).
Пример
В данном случае (divoverrightarrow A) в любой точке поля обозначает предел отношения потока вектора (overrightarrow A) через замкнутую поверхность (S), которая охватывает точку (M), к объему (triangle V) части поля, ограничиваемой поверхностью (S), при неограниченном уменьшении (triangle V) :
(divoverrightarrow A=lim_{triangle Vrightarrow0}frac1{triangle V}oint(overrightarrow Adoverrightarrow S)).
Вернемся к заряду. Предположим, что он распределен в пространстве (triangle V), а его объемная плотность (<rho>), тогда в соответствии с теоремой Остроградского-Гаусса:
(oint(overrightarrow Edoverrightarrow S)=frac q{varepsilon_0}) или же( oint(overrightarrow Edoverrightarrow S)=frac{<rho>triangle V}{varepsilon_0}).
Если устремить (triangle V) к (0), притягивая его к нужной нам точке, то в этом случае (<rho>) в этом точке будет стремиться к (rho), то есть (frac{<rho>}{varepsilon_0}rightarrowfracrho{varepsilon_0}.)
Дивергенцией вектора (overrightarrow E) называется величина, которая является пределом отношения (oint(overrightarrow Edoverrightarrow S)) к ( triangle V) при (triangle Vrightarrow0) . Обозначается это как (divoverrightarrow E) и соответствует (divoverrightarrow E;=;lim_{triangle Vrightarrow0}frac1{triangle V}oint(overrightarrow Edoverrightarrow S))
Этим же способом определяется дивергенция любого векторного поля.
Применение формулы
Формула используется для того, чтобы преобразовать объемный интеграл в интеграл по замкнутой поверхности и наоборот.
В матанализе формула теоремы Остроградского-Гаусса используется для вычисления дивергенции, то есть потока векторного поля через поверхность окрестности по внешним направлениям. Принимая во внимание то, что поток векторного поля через замкнутую поверхность (delta) в направлении внешней единичной нормали (overline{n_0}) равен дивергенции данного поля, вычисленной по телу (T), которое эта поверхность
Применение теоремы
Для расчета электростатического поля
Теорема Остроградского-Гаусса применяется для расчета электростатического поля для тех задач, где поле имеет специальную симметрию. Например, плоскую, цилиндрическую или сферическую. В данном случае на эффективность применения теоремы влияют симметрия и конфигурация поля, которые должны соответствовать двум условиям:
- заряженное тело должно быть окружено простой замкнутой поверхностью;
- вычисление потока вектора напряженности необходимо свести к умножению (Е) (или (E_n)) на площадь поверхности (S) или часть нее.
Если исходные данные не соответствуют условиям, то при решении задачи необходимо использовать другие методы.
Для плоскости
Рассмотрим применение теоремы для равномерно заряженной плоскости.
Задача
Предположим, что заряд положительный, а плоскость заряжена с постоянной поверхностной плотностью, что выражается в формуле (delta=frac{dq}{dS}). Благодаря симметрии можно сделать вывод, что напряженность в любой точке поля обладает направлением, перпендикулярным плоскости. Из этого же можно сделать вывод, что во всех точках, симметричных плоскости, напряженность поля одинакова, но ее направление противоположно.
Отметим на заряженной плоскости площадь (triangle S). Определим вокруг площадки замкнутую цилиндрическую поверхность (рисунок 3) так, чтобы ее образующие основания были перпендикулярны плоскости, располагались симметрично, относительно нее и имели величину (triangle S).
А теперь используем теорему Остроградского-Гаусса: (oint_SE_ndS=frac1{varepsilon_0}{textstylesum_{}^{}}q_1). Так как в этом случае (E_n=0) в каждой точке, через боковую часть потока не будет. В случае оснований (E_n=E), а исходя из этого совокупный поток через поверхность равен (2Etriangle S).
Посмотрим теперь внутрь поверхности. Там заключен заряд (deltatriangle S). В соответствии с теоремой Остроградского-Гаусса, должно быть выполнено условие: (2Etriangle S=frac{deltatriangle S}{varepsilon_0}), из чего следует (E=fracdelta{2varepsilon_0}).
Так как напряженность поля равна на любых расстояниях от плоскости, в вычисления не нужно включать длину цилиндра. Если плоскость заряжена, то направление векторов изменяется на противоположное.
Для сферической поверхности
Задача
Возьмем поле, которое создает сферическая поверхность с радиусом (R), заряженное с постоянной поверхностной плоскость (delta). Так как этому полю характерна центральная симметрия, направление вектора (overrightarrow E) в любой точке проходит через центр сферы. Учитывая это, мы знаем, что значение напряженности можно выразить функцией расстояния (r) от центра сферы.
Вычислим напряженность поля. Для начала расчетов проведем через точки на A и B (на рисунке 1.1) сферические поверхности для вычисления потока вектора, проходящего через них. Точка B располагается внутри заряженной поверхности, а ее расстояние от центра составляет (r) (при( r<R)). Внутри поверхности, которую мы провели через эту точки, заряд содержаться не будет, а, значит, по теореме Остроградского-Гаусса (oint_SE_ndS=frac1{varepsilon_0}{textstylesum_{}^{}}q_1), напряженность в этой точки будет равняться нулю.
Теперь обратимся к полю, созданному заряженной сферической поверхностью в точке A, чье расстояние от центра сферы равно (r). Поместим заряженное тело в замкнутое сферическую поверхность радиусом r, проходящей через точку A. В этом случае (E_n=E(r)) справедливо для всех точек этой поверхности. Заряд (q), создающий данное поле, пропадает внутри этой поверхности. Таким образом, (E(r)4mathrm{πr}^2=frac{mathrm q}{{mathrmvarepsilon}_0},;mathrm{потому};mathrm{что};oint(overrightarrow{mathrm E}mathrm doverrightarrow{mathrm S})=frac{sum_{}{mathrm q}_1}{{mathrmvarepsilon}_0}). Из этого следует, что напряженность поля в точках, располагающихся на расстоянии (r>R), равняется (E=frac1{4pivarepsilon_0}frac q{r^2}).
В диэлектрике
Диэлектрики влияют на электрического поле. Это влияние выражается в ответном действии поляризационных зарядов, которые возникают в поле. Исходя из этого теорему Остроградского-Гаусса для тел в вакууме можно видоизменить, прибавив к свободным зарядам поляризационные, и тогда эту теорему можно применять в диэлектрической среде.
Теорема будет выглядеть так: (oint_soverrightarrow Ddoverrightarrow S=sum_{i=1}^Nq_i=Q(2))
В этом случае (overrightarrow D) — это вектор электрического смещения, (q_i) — это свободные заряды, а (Q) — суммарный свободный заряд, находящийся внутри объема, ограниченного поверхностью (S). В вакууме векторы (overrightarrow D) и (overrightarrow E) совпадают.
Для расчета магнитного поля
Задача
Выделим элементарную бесконечно малую площадку (dS) в магнитном поле. Предположим, что она настолько маленькая и плоская, что вектор B можно признать одинаковым по величине и направлению в каждой точке магнитного поля, независимо от того однородно оно или нет.
Тогда поток вектора магнитной индукции сквозь (dS) можно определить с помощью выражения (dphi=BdScosleft(overrightarrow Bwedge doverrightarrow Sright)=B_ndS=overrightarrow Bdoverrightarrow S ).
В данном случае (B_n) равно (Bcosleft(alpharight)), где (alpha) это острый угол между направлениями вектора (В) и нормалью. (B_n) — это проекция вектора магнитной индукции в области нахождения площадки (dS) на направление нормали (рисунок 4).
Определение потока магнитной индукции через произвольную поверхность звучит как сумма потоков через элементарные площадки, на которые разбита эта поверхность, и выражается в виде интеграла по этой поверхности:
Области применения теоремы
Ценность теоремы Остроградского-Гаусса состоит в формулировке общих свойств электрического поля. Она — один из основных постулатов теории электричества. Поэтому широко применяется в общей и учебной физике и таких ее областях как электромагнетизм, электростатика и механика, с ее помощью решают задачи и изучают векторные (в том числе электромагнитные) поля.
Кроме этого теорема применяется в электродинамике, гидродинамике и математическом анализе.
Поляризация
диэлектриков
Диэлектрики — это вещества,
которые практически не проводят
электрический ток. Поведение
диэлектриков в электрическом поле
определяется их внутренним
строением. Как известно, мельчайшей
частицей вещества, сохраняющей его
химические свойства, является
молекула. Молекулы состоят из
атомов, в состав которых входят
положительно заряженные ядра и
отрицательно заряженные электроны.
В целом молекулы нейтральны.
Согласно теории ковалентных связей
устойчивость молекул достигается
путем образования одной или
нескольких пар электронов, которые
становятся общими для
соединяющихся атомов, т. е. входят
одновременно в состав оболочек
двух атомов.
Для каждого рода зарядов —
положительных (ядер) и
отрицательных (электронов) — можно
найти такую точку, которая будет
являться как бы их
«электрическим центром
тяжести». Эти точки называются
полюсами молекулы. Если в молекуле
электрические центры тяжести
положительных и отрицательных
зарядов совпадут, то молекула будет
неполярной. Но если
молекула построена несимметрично,
например состоит из двух
разнородных атомов, то общая пара
электронов может быть в большей или
меньшей степени смещена в сторону
одного из атомов. Очевидно, что в
этом случае, вследствие
неравномерного распределения
положительных и отрицательных
зарядов внутри молекулы, их
электрические центры тяжести не
совпадут и получится молекула,
называемая полярной.
Для описания макроскопических
электрических свойств
диэлектриков достаточно
ограничиться представлением о том,
что в них отсутствуют свободные
носители заряда, и при помещении
диэлектрика в электрическое поле в
материале возбуждается множество
микроскопических диполей. В
случае неполярных молекул это
происходит путем смещения в
пределах молекул их положительных
зарядов в направлении внешнего
поля и отрицательных в
противоположном направлении (рис.
5.1).
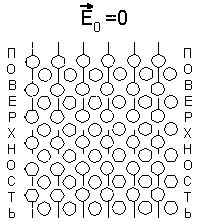 |
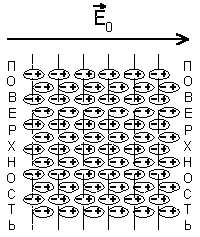 |
|
Рис. 5.1 |
Приобретаемый молекулой
дипольный момент пропорционален
напряженности поля, в котором
находится молекула. В системе СИ он
записывается, как
| (5.1) |
где коэффициент
пропорциональности β
называется поляризуемостью
молекулы.
Для вещества, состоящего из
полярных молекул, под действием
момента сил (3.9)
происходит преимущественное
выстраивание молекул в направлении
внешнего поля. В обоих случаях
(неполярных и полярных молекул) в
результате появляется дипольный
момент и у всего объема
диэлектрика. Средний
дипольный момент, индуцированный
полем в единице объема, называется
поляризованностью диэлектрика:
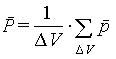 |
(5.2) |
где суммирование производится по
всем молекулам, находящимся в
объеме ΔV, а
дипольный момент p каждой
молекулы определяется
суммированием по всем заряженным
частицам, входящим в молекулу:
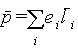 |
(5.3) |
где ei — заряд
каждой частицы, а li
— ее смещение под действием
электрического поля.
Домножив и разделив правую часть
(5.2) на число молекул ΔN,
находящихся в объеме ΔV,
получим еще одно выражение для
поляризованности:
| (5.4) |
где n = ΔN / ΔV — концентрация
молекул, а < p > — средний
диполный момент молекулы.
Вообще говоря, P меняется
в диэлектрике от точки к точке, но
для широкого класса веществ в
каждой точке P ~ E.
Существуют вещества, обладающие
поляризованностью и в отсутствие
внешнего поля, однако здесь они не
рассматриваются.
Поскольку в целом молекулы
нейтральны, то именно дипольный
момент и определяет электрическое
поле, создаваемое самим материалом,
когда его помещают во внешнее поле.
В силу принципа
суперпозиции поле внутри
диэлектрика есть сумма внешнего
поля и поля от всех диполей,
индуцированных в диэлектрике:
| (5.5) |
где E0 —
напряженность поля сторонних
зарядов, а E’ — связанных
зарядов. Связанными
зарядами называются
нескомпенсированные заряды,
появляющиеся в результате
поляризации молекул диэлектрика,
тогда как сторонними — свободные
заряды, находящиеся в диэлектрике
или вне его. E0 и E’
представляют собой макрополя,
т.е. усредненные по некоторому
малому объему микрополя,
создаваемые сторонними и
связанными зарядами,
соответственно.
Так как каждая молекула
поляризуется под воздействием как
поля сторонних зарядов, так и поля,
создаваемого всеми другими
поляризованными молекулами, то
поляризованность диэлектрика
пропорциональна напряженности
именно суммарного поля (5.5):
| (5.6) |
где греческой буквой «каппа»
обозначена, так называемая,
диэлектрическая восприимчивость.
Для изотропных диэлектриков κ — просто коэффициент, и
векторы P и E в
этом случае совпадают по
направлению. В общем случае это не
так. Заметим, что
пропорциональность
поляризованности напряженности
поля имеет место для широкого
класса диэлектриков, однако
существуют вещества
(сегнетоэлектрики) для которых
зависимость P от E имеет
гораздо более сложный характер, чем
(5.6). Здесь они не рассматриваются.
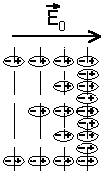
Рис. 5.2 |
При поляризации однородного диэлектрика (см. рис. 5.1) смещения зарядов внутри любого выбранного слоя внутри диэлектрика происходят таким образом, что количество связанного заряда, покидающего слой, равно заряду, входящему в него. Таким образом объемный заряд внутри диэлектрика не образуется. В поверхностных же слоях образуется связанный поверхностный заряд . В случае же неоднородного диэлектрика в каждый слой, мысленно выделенный внутри материала, с одной стороны входит больше заряда, чем выходит с другой, и связанный заряд образуется не только на поверхности, но и в объеме диэлектрика, как это показано на рис. 5.2. |
Теорема
Гаусса для вектора P
Выделим внутри диэлектрика
некоторый объем V,
ограниченный поверхностью S.
Подсчитаем, сколько заряда
проходит через элемент dS воображаемой
поверхности, когда материал
поляризуется. При появлении
электрического поля положительные
заряды молекул сместятся на
некоторое расстояние вдоль
поля, а отрицательные — в
противоположном направлении. При
этом каждая молекула приобретет
дипольный момент, определяемый
соотношением (5.3),
причем вектор смещения будет
направлен вдоль поля, а средняя
длина вектора смещения l
для диполей, находящихся в
прилегающем к dS слою, будет
согласно (5.4) связана с
поляризацией этого слоя
соотношением
| (5.7) |
откуда l = P/ne.
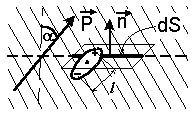
Рис. 5.3 |
Элемент поверхности dS пересечет все те диполи, центры которых расположены в прилегающем к нему слое толщины l |cos α| , где α — угол между нормалью к dS и направлением вектора поляризованности (рис. 5.3). Объем этого слоя равен l |cos α|dS, а число пересекаемых элементом dS диполей равно n l |cos α|dS. |
Следовательно, для выбранного
элемента поверхности
соответствующая абсолютная
величина нескомпенсированного
заряда внутри объема V равна
| (5.8) |
При этом, если cos α
> 0, то снаружи от элемента dS находятся
положительные заряды, а внутри —
отрицательные, а если cos α
< 0, то — наоборот.
Таким образом
алгебраическая величина
нескомпенсированного заряда
внутри объема V равна dq’ = -Pn
dS = — P dS. Тогда
поток вектора P через
поверхность S, ограничивающую
объем V, связан с полным
связанным зарядом q‘ в объеме
соотношением
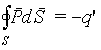 |
(5.9) |
Последнее соотношение
представляет собой теорему
Гаусса для вектора P.
Преобразуем левую часть
выражения (5.9) по теореме Остроградского-Гаусса,
а связанный заряд q’ представим,
как
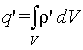 |
(5.10) |
где ρ‘ — объемная
плотность связанного заряда.
Тогда будем иметь
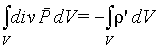 |
(5.11) |
откуда с учетом произвольности
выбранного объема V получим теорему Гаусса для вектора
поляризованности в
дифференциальной форме:
| (5.12) |
Выясним, в каких случаях объемная
плотность связанных зарядов
отлична от нуля. Выразим P
в (5.12) через E согласно (5.6)
| ρ‘ = –∇(κεoE) = –εo∇(κE) = –εo(E∇κ+κ∇E) |
(5.13) |
В теореме Гаусса для вектора E,
записанной в дифференциальной
форме (2.17),
в правой части стоит объемная
плотность заряда, включающая в
случае диэлектрика как плотность
сторонних, так и связанных зарядов
Заменяя в (5.13) ∇E
согласно (5.14) получим
| ρ‘ = –εoE∇κ – κρ –κρ‘ |
(5.15) |
Отсюда
| ρ‘ = – (εoE∇κ + κρ)/(1+κ) | (5.16) |
Из последнего выражения видно,
что объемная плотность связанного
заряда в диэлектрике отлична от
нуля в двух случаях: (1) когда
диэлектрик поляризуется
неоднородно (κ есть
функция координаты) и/или (2) в
диэлектрике присутствует
сторонний заряд (ρ отлично
от нуля). При однородной
поляризации и отсутствии
стороннего заряда внутри
диэлектрика равенство нулю
связанного объемного заряда легко
усматривается из рис. 5.1.
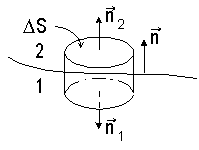
Рис. 5.4 |
Рассмотрим границу раздела двух однородных изотропных диэлектриков 1 и 2 (рис. 5.4). Выделим мысленно на границе раздела цилиндр с площадью основания ΔS с образующей, перпендикулярной границе раздела. Выберем произвольно направление нормали n к границе, как показано на рисунке. Пусть площадка ΔS, вырезаемая цилиндром на границе, столь мала, что ее можно считать плоской, а поляризованность каждого из диэлектриков в ее пределах постоянной. |
Найдем
поток Ф вектора P через
поверхность цилиндра. Поток через
нижнее основание цилиндра равен P1·ΔS cos (P1,
n1), а через
верхнее P2·ΔS
cos (P2, n2),
где индексами 1 и 2 обозначены
величины, относящиеся
соответственно к внутренней и
внешней по отношению к нормали
n сторонам границы раздела.
Поток через боковую поверхность
цилиндра обозначим Ф’. Тогда будем
иметь
| (5.17) |
Направление нормали n2
совпадает с направлением нормали n,
а направление нормали n1
прямо противоположно.
Следовательно
| P1·ΔS cos (P1, n1) = —P1n ; |
P2·ΔS cos (P2, n2)=P2n , |
где P1n и P2n
— проекции вектров P1и
P2 на нормаль n.
Таким образом
Ф= (P2n — P1n
) ΔS + Ф’.
Будем теперь уменьшать
высоту цилиндра, не изменяя при
этом его основания. Поток Ф’ через
безгранично уменьшающуюся боковую
поверхность будет стремиться к
нулю, так что общий поток через
поверхность цилиндра сведется в
пределе к потоку через его
основания:
Ф= (P2n — P1n
) ΔS .
Для однородных
диэлектриков объемный связанный
заряд, как было показано
выше, равен нулю. Стало быть
внутри цилиндра окажется заряд,
расположенный на границе раздела
на элементе поверхности ΔS.
Этот заряд равен ΔS ·σ‘, где σ‘ — поверхностная
плотность связанного заряда на
границе раздела диэлектриков. На
основании теоремы Гаусса
для вектора P запишем
(P2n — P1n
) ΔS = —ΔS ·σ‘,
откуда
| (P2n — P1n ) = — σ‘ |
(5.18) |
Иными словами,
на границе раздела нормальная
составляющая вектора P
испытывает разрыв, величина
которого зависит от σ‘.
В частности, если среда 2 вакуум, то P2n
= 0 и
где Pn проекция
вектора P на внешнюю
нормаль к поверхности данного
диэлектрика.
Вектор D
В случае диэлектрика теорема Гаусса для
вектора E запишется
как
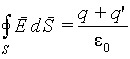 |
(5.20) |
где q и q‘ — находящиеся
внутри поверхности S полные
сторонний и связанный заряды,
соответственно. Поскольку
связанный заряд в диэлектрике
индуцируется под воздействием
искомого поля E, то
применение теоремы Гаусса в виде
(5.20) для определения напряженности
поля становится практически
невозможным. Для преодоления
указанной трудности вводится
вспомогательный вектор D.
Логика определения этого вектора
вытекает из следующих соображений.
Выразим связанный заряд в (5.20)
согласно (5.9)
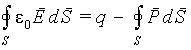 |
(5.21) |
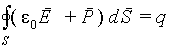 |
(5.22) |
Как видно из (5.22) если
ввести вспомогательный вектор в
виде D = ε0E+P, то
его поток будет определяться
только сторонним зарядом,
распределение которого
предполагается известным. Тогда
для вектора D
теорема Гаусса имеет вид
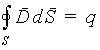 |
(5.23) |
Пользуясь теми же соображениями,
что и при переходе от интегральной
формы теоремы Гаусса для вектора P
к дифференциальной, запишем теорему Гаусса для вектора
D в дифференциальной форме
| (5.24) |
Для изотропного
диэлектрика P = κε0E. Тогда
| (5.25) |
или
| (5.26) |
где обозначено ε = 1+κ — диэлектрическая
проницаемость вещества. Для всех
диэлектриков ε > 0.
Для вакуума ε = 1.
Условия
на границе двух диэлектриков
Рассмотрим поведение векторов E
и D на границе раздела
однородных изотропных
диэлектриков.
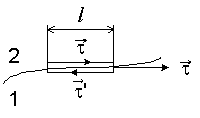
Рис. 5.5 |
Для установления связи между тангенциальными составляющими вектора E по обе стороны границы воспользуемся теоремой о циркуляции вектора E. Выберем контур небольшой длины l, как показано на рис. 5.5 и в предположении, что векторы E1 и E2 с обеих сторон границы постоянны в пределах контура, запишем на основании этой теоремы |
| E2τ + E1τ‘ + C’ = 0 |
(5.27) |
где проекции вектора E
взяты в непосредственной близости
от границы раздела на направление
обхода контура, указанное на
рисунке стрелками, а C’ — вклад в
циркуляцию от перпендикулярных к
границе сторон контура. В пределе
при стремящейся к нулю высоте
контура этим вкладом можно
пренебречь и тогда
Если внутри диэлектрика 1
проекцию вектора E взять
не на орт τ‘, а на
общий орт τ, то так
как E1τ‘
= -E1τ
, то получим
или
Иными словами, тангенциальная
составляющая вектора E
одинакова по обе стороны границы
раздела.
Заменив согласно (5.26)
проекции вектора E проекциями
вектора D, деленными на εoε, получим
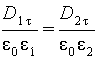 |
(5.31) |
откуда
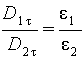 |
(5.32) |
Обратимся теперь к
нормальной составляющей вектора D.
Воспользуемся для этого теоремой
Гаусса для этого вектора. Выбирая
поверхность интегрирования как
показано на рис. 5.4 и
следуя тем же рассуждениям, которые
привели к выражению (5.18),
получим
Из этого соотношения следует, что
при наличии на границе раздела
стороннего заряда с поверхностной
плотностью σ нормальная
составляющая вектора D
терпит разрыв. При отсутствии
стороннего заряда на границе
Нормальные составляющие вектора E
с разных сторон границы раздела
относятся тогда на основании (5.26) , как
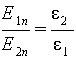 |
(5.35) |
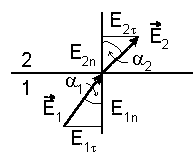
Рис. 5.6 |
Как следует из полученных соотношений (5.30) и (5.35) нормальная и тангенциальная составляющие вектора E на границе раздела ведут себя по разному. В результате линии вектора E испытывают преломление (рис. 5.6). Найдем соотношение между углами α1 и α2 для случая, когда сторонних зарядов на границе раздела нет. Как видно из рисунка
|
Отсюда на основании (5.30) и (5.35)
получаем
| (5.37) |
Если на среда 1 — проводник, а 2 —
диэлектрик, то из соотношения (5.33) следует, что
Dn =σ,
где n — внешняя к проводнику
нормаль. Действительно, т.к. в
проводнике E=0, то и P=0.
Тогда, так как D = ε0E+P, то
и D1n =0.
Если к заряженному проводнику
прилегает однородный диэлектрик,
то на границах диэлектрика
выступают связанные поверхностные
заряды. Найдем их поверхностную
плотность σ‘. Следуя
рассуждениям, которые привели к
выводу соотношения (4.1), в
данном случае получим для
нормальной составляющей вектора E
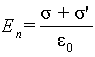 |
(5.38) |
Но
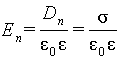 |
(5.39) |
С учетом (5.39) из (5.38) получим
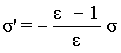 |
(5.40) |
Поле
внутри однородного изотропного
диэлектрика
Если однородный и
изотропный диэлектрик полностью
заполняет объем, ограниченный
эквипотенциальными поверхностями
поля сторонних зарядов, то
напряженность поля внутри
диэлектрика в ε раз
меньше, чем напряженность поля
сторонних зарядов.
Продемонстрируем справедливость
приведенного утверждения на
примере плоского конденсатора. Предположим, что
пространство между обкладками
плоского конденсатора заполнено однородным и
изотропным диэлектриком. Тогда на
поверхности диэлектрика,
прилегающей к пластине с
положительным зарядом, появится
индуцированный связанный
отрицательный заряд, а на
противоположной поверхности
диэлектрика – индуцированный
связанный положительный заряд.
Этот связанный заряд σ‘ является источником
электрического поля с
напряженностью
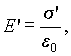 |
(5.41) |
причем, согласно (5.19), σ‘
= Pn, где Pn
– нормальная
составляющая вектора
поляризованности.
В результате, в
силу принципа суперпозиции поле
внутри диэлектрика окажется
векторной суммой полей,
создаваемых сторонним зарядом,
находящимся на обкладках
конденсатора, и поверхностным
связанным зарядом:
E=E0+E‘,
причем векторы
E0 и E‘ коллинеарны и
направлены навстречу друг другу.
Поэтому модуль вектора
напряженности будет равен
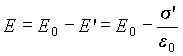 |
(5.42) |
Так как
диэлектрик предполагается
однородным и изотропным, то
поляризованность диэлектрика
пропорциональна напряженности
поля:
P=κ ε 0E .
Поскольку
диэлектрик полностью заполняет
объем, ограниченный
эквипотенциальными поверхностями
поля сторонних зарядов, то вектор E на границе между
проводящей обкладкой конденсатора
и прилегающим к ней диэлектриком
перпендикулярен границе, т.е.
E=En .
Тогда, с учетом
того, что σ‘ = Pn получается
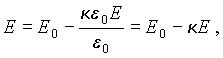 |
(5.43) |
откуда для
напряженности поля внутри
конденсатора имеем
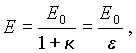 |
(5.44) |
где ε — диэлектрическая
проницаемость диэлектрика.
Сайт управляется системой uCoz