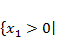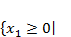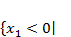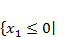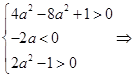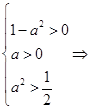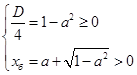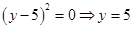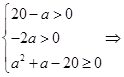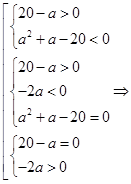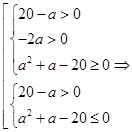��������: 1 2 3 4 5 6 7 >> [����� �����: 49]
��� ����� a � b ��������� x3 + ax + b = 0 ����� ��� ��������� �������, ������������ �������������� ����������?
������ 61257 |
���������: 3 ������: 8,9,10 |
��������, ��� ��������� x³ + ax² – b = 0, ��� a � b ������������ � b > 0, ����� ���� � ������ ���� ������������� ������.
������
66600 |
���������: 3 ������: 8,9,10,11 |
��������� $P(x)=x^3+ax^2+bx+c$ ����� ��� ��������� �������������� �����, ���������� �� ������� ����� ����� ���� ������. ��������, ��� $c>ab$.
��������� ������� ������� ����� ��� ��������� ����� ������ ����� 0 � 1. ������� ������� �������� ��� �� ���� ������.
�ݣ �� ������� ��� ������ ������������ ����������, �� �� ������, � ����� ������� ��� ������������ ����. ����������� �� ����� ������������ ������ ������?
����� a, b, c – ������� ������������, p – ���
������������, � r � R – ������� ��������� � ���������
����������� ��������������. ��������� ��������� � ��������������, ���������� �� p, r, R, ������� �������� �������� ����� a, b, c. �������� ���������
��������: 1 2 3 4 5 6 7 >> [����� �����: 49]
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
2
Аналоги к заданию № 158: 159 Все
3
Применяя теоремы Виета, решите следующие задачи. При каких значениях а сумма корней уравнения равна нулю?.
4
Применяя теоремы Виета, решите следующие задачи При каких значениях а сумма корней уравнения равна нулю?.
Аналоги к заданию № 160: 161 Все
5
Применяя теоремы Виета, решите следующие задачи. При каких значениях а произведение корней уравнения равно нулю?.
Пройти тестирование по этим заданиям
В квадратных уравнениях существует целый ряд соотношений. Основными являются отношения между корнями и коэффициентами. Также в квадратных уравнениях работает ряд соотношений, которые задаются теоремой Виета.
В этой теме мы приведем саму теорему Виета и ее доказательство для квадратного уравнения, теорему, обратную теореме Виета, разберем ряд примеров решения задач. Особое внимание в материале мы уделим рассмотрению формул Виета, которые задают связь между действительными корнями алгебраического уравнения степени n и его коэффициентами.
Формулировка и доказательство теоремы Виета
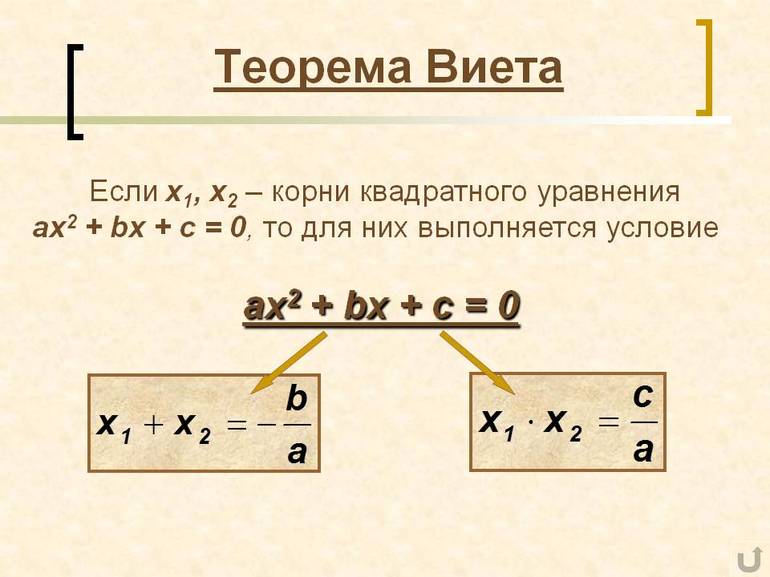
Формула корней квадратного уравнения a·x2+b·x+c=0 вида x1=-b+D2·a, x2=-b-D2·a, где D=b2−4·a·c, устанавливает соотношения x1+x2=-ba, x1·x2=ca. Это подтверждает и теорема Виета.
В квадратном уравнении a·x2+b·x+c=0, где x1 и x2 – корни, сумма корней будет равна соотношению коэффициентов b и a, которое было взято с противоположным знаком, а произведение корней будет равно отношению коэффициентов c и a, т. е. x1+x2=-ba, x1·x2=ca.
Предлагаем вам следующую схему проведения доказательства: возьмем формулу корней, составим суму и произведение корней квадратного уравнения и затем преобразуем полученные выражения для того, чтобы убедиться, что они равны -ba и ca соответственно.
Составим сумму корней x1+x2=-b+D2·a+-b-D2·a. Приведем дроби к общему знаменателю -b+D2·a+-b-D2·a=-b+D+-b-D2·a. Раскроем скобки в числителе полученной дроби и приведем подобные слагаемые: -b+D+-b-D2·a=-b+D-b-D2·a=-2·b2·a. Сократим дробь на: 2-ba=-ba.
Так мы доказали первое соотношение теоремы Виета, которое относится к сумме корней квадратного уравнения.
Теперь давайте перейдем ко второму соотношению.
Для этого нам необходимо составить произведение корней квадратного уравнения: x1·x2=-b+D2·a·-b-D2·a.
Вспомним правило умножения дробей и запишем последнее произведение следующим образом: -b+D·-b-D4·a2.
Проведем в числителе дроби умножение скобки на скобку или же воспользуемся формулой разности квадратов для того, чтобы преобразовать это произведение быстрее: -b+D·-b-D4·a2=-b2-D24·a2.
Воспользуемся определением квадратного корня для того, чтобы осуществить следующий переход: -b2-D24·a2=b2-D4·a2. Формула D=b2−4·a·c отвечает дискриминанту квадратного уравнения, следовательно, в дробь вместо D можно подставить b2−4·a·c:
b2-D4·a2=b2-(b2-4·a·c)4·a2
Раскроем скобки, приведем подобные слагаемые и получим: 4·a·c4·a2. Если сократить ее на 4·a, то остается ca. Так мы доказали второе соотношение теоремы Виета для произведения корней.
Запись доказательства теоремы Виета может иметь весьма лаконичный вид, если опустить пояснения:
x1+x2=-b+D2·a+-b-D2·a=-b+D+-b-D2·a=-2·b2·a=-ba,x1·x2=-b+D2·a·-b-D2·a=-b+D·-b-D4·a2=-b2-D24·a2=b2-D4·a2==D=b2-4·a·c=b2-b2-4·a·c4·a2=4·a·c4·a2=ca.
При дискриминанте квадратного уравнения равном нулю уравнение будет иметь только один корень. Чтобы иметь возможность применить к такому уравнению теорему Виета, мы можем предположить, что уравнение при дискриминанте, равном нулю, имеет два одинаковых корня. Действительно, при D=0 корень квадратного уравнения равен: -b2·a, тогда x1+x2=-b2·a+-b2·a=-b+(-b)2·a=-2·b2·a=-ba и x1·x2=-b2·a·-b2·a=-b·-b4·a2=b24·a2, а так как D=0, то есть, b2-4·a·c=0, откуда b2=4·a·c, то b24·a2=4·a·c4·a2=ca.
Чаще всего на практике теорема Виета применяется по отношению к приведенному квадратному уравнению вида x2+p·x+q=0, где старший коэффициент a равен 1. В связи с этим и формулируют теорему Виета именно для уравнений такого вида. Это не ограничивает общности в связи с тем, что любое квадратное уравнение может быть заменено равносильным уравнением. Для этого необходимо поделить обе его части на число a, отличное от нуля.
Приведем еще одну формулировку теоремы Виета.
Сумма корней в приведенном квадратном уравнении x2+p·x+q=0 будет равна коэффициенту при x, который взят с противоположным знаком, произведение корней будет равно свободному члену, т.е. x1+x2=−p, x1·x2=q.
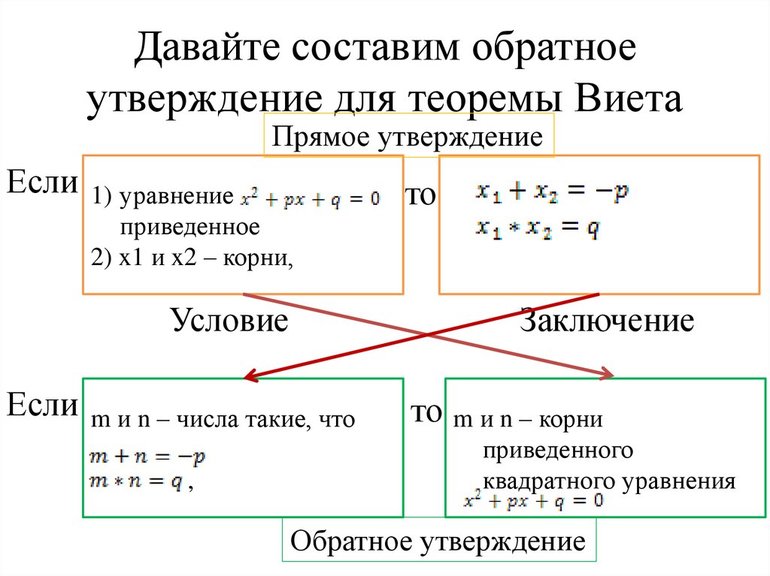
Теорема, обратная теореме Виета
Если внимательно посмотреть на вторую формулировку теоремы Виета, то можно увидеть, что для корней x1 и x2 приведенного квадратного уравнения x2+p·x+q=0 будут справедливы соотношения x1+x2=−p, x1·x2=q. Из этих соотношений x1+x2=−p, x1·x2=q следует, что x1 и x2 – это корни квадратного уравнения x2+p·x+q=0. Так мы приходим к утверждению, которое является обратным теореме Виета.
Предлагаем теперь оформить это утверждение как теорему и провести ее доказательство.
Если числа x1 и x2 таковы, что x1+x2=−p и x1·x2=q, то x1 и x2 являются корнями приведенного квадратного уравнения x2+p·x+q=0.
Замена коэффициентов p и q на их выражение через x1 и x2 позволяет преобразовать уравнение x2+p·x+q=0 в равносильное ему x2−(x1+x2)·x+x1·x2=0.
Если в полученное уравнение подставить число x1 вместо x, то мы получим равенство x12−(x1+x2)·x1+x1·x2=0. Это равенство при любых x1 и x2 превращается в верное числовое равенство 0=0, так как x12−(x1+x2)·x1+x1·x2=x12−x12−x2·x1+x1·x2=0. Это значит, что x1 – корень уравнения x2−(x1+x2)·x+x1·x2=0, и что x1 также является корнем равносильного ему уравнения x2+p·x+q=0.
Подстановка в уравнение x2−(x1+x2)·x+x1·x2=0 числа x2 вместо x позволяет получить равенство x22−(x1+x2)·x2+x1·x2=0. Это равенство можно считать верным, так как x22−(x1+x2)·x2+x1·x2=x22−x1·x2−x22+x1·x2=0. Получается, что x2 является корнем уравнения x2−(x1+x2)·x+x1·x2=0, а значит, и уравнения x2+p·x+q=0.
Теорема, обратная теореме Виета, доказана.
Примеры использования теоремы Виета
Давайте теперь приступим к разбору наиболее типичных примеров по теме. Начнем с разбора задач, которые требуют применения теоремы, обратной теореме Виета. Ее можно применять для проверки чисел, полученных в ходе вычислений, на предмет того, являются ли они корнями заданного квадратного уравнения. Для этого необходимо вычислить их сумму и разность, а затем проверить справедливость соотношений x1+x2=-ba, x1·x2=ac.
Выполнение обоих соотношений свидетельствует о том, что числа, полученные в ходе вычислений, являются корнями уравнения. Если же мы видим, что хотя бы одно из условий не выполняется, то данные числа не могут быть корнями квадратного уравнения, данного в условии задачи.
Какая из пар чисел 1) x1=−5, x2=3, или 2) x1=1-3, x2=3+3, или 3) x1=2+72, x2=2-72 является парой корней квадратного уравнения 4·x2−16·x+9=0?
Решение
Найдем коэффициенты квадратного уравнения 4·x2−16·x+9=0. Это a=4, b=−16, c=9. В соответствии с теоремой Виета сумма корней квадратного уравнения должна быть равна -ba, то есть, 164=4, а произведение корней должно быть равно ca, то есть, 94.
Проверим полученные числа, вычислив сумму и произведение чисел из трех заданных пар и сравнив их с полученными значениями.
В первом случае x1+x2=−5+3=−2. Это значение отлично от 4, следовательно, проверку можно не продолжать. Согласно теореме, обратной теореме Виета, можно сразу сделать вывод о том, что первая пара чисел не является корнями данного квадратного уравнения.
Во втором случае x1+x2=1-3+3+3=4. Мы видим, что первое условие выполняется. А вот второе условие нет: x1·x2=1-3·3+3=3+3-3·3-3=-2·3. Значение, которое мы получили, отлично от 94. Это значит, что вторая пара чисел не является корнями квадратного уравнения.
Перейдем к рассмотрению третьей пары. Здесь x1+x2=2+72+2-72=4 и x1·x2=2+72·2-72=22-722=4-74=164-74=94. Выполняются оба условия, а это значит, что x1 и x2 являются корнями заданного квадратного уравнения.
Ответ: x1=2+72, x2=2-72
Мы также можем использовать теорему, обратную теореме Виета, для подбора корней квадратного уравнения. Наиболее простой способ – это подбор целых корней приведенных квадратных уравнений с целыми коэффициентами. Можно рассматривать и другие варианты. Но это может существенно затруднить проведение вычислений.
Для подбора корней мы используем тот факт, что если сумма двух чисел равна второму коэффициенту квадратного уравнения, взятому со знаком минус, а произведение этих чисел равно свободному члену, то эти числа являются корнями данного квадратного уравнения.
В качестве примера используем квадратное уравнение x2−5·x+6=0. Числа x1 и x2 могут быть корнями этого уравнения в том случае, если выполняются два равенства x1+x2=5 и x1·x2=6. Подберем такие числа. Это числа 2 и 3, так как 2+3=5 и 2·3=6. Получается, что 2 и 3 – корни данного квадратного уравнения.
Теорему, обратную теореме Виета, можно использовать для нахождения второго корня, когда первый известен или очевиден. Для этого мы можем использовать соотношения x1+x2=-ba, x1·x2=ca.
Рассмотрим квадратное уравнение 512·x2−509·x−3=0. Необходимо найти корни данного уравнения.
Решение
Первым корнем уравнения является 1, так как сумма коэффициентов этого квадратного уравнения равна нулю. Получается, что x1=1.
Теперь найдем второй корень. Для этого можно использовать соотношение x1·x2=ca. Получается, что 1·x2=−3512, откуда x2=-3512.
Ответ: корни заданного в условии задачи квадратного уравнения 1 и -3512.
Подбирать корни, используя теорему, обратную теореме Виета, можно лишь в простых случаях. В остальных случаях лучше проводить поиск с использованием формулы корней квадратного уравнения через дискриминант.
Благодаря теореме, обратной теореме Виета, мы также можем составлять квадратные уравнения по имеющимся корням x1 и x2. Для этого нам необходимо вычислить сумму корней, которая дает коэффициент при x с противоположным знаком приведенного квадратного уравнения, и произведение корней, которое дает свободный член.
Напишите квадратное уравнение, корнями которого являются числа −11 и 23.
Решение
Примем, что x1=−11 и x2=23. Сумма и произведение данных чисел будут равны: x1+x2=12 и x1·x2=−253. Это значит, что второй коэффициент -12, свободный член −253.
Составляем уравнение: x2−12·x−253=0.
Ответ: x2−12·x−253=0.
Мы можем использовать теорему Виета для решения заданий, которые связаны со знаками корней квадратных уравнений. Связь между теоремой Виета связана со знаками корней приведенного квадратного уравнения x2+p·x+q=0 следующим образом:
- если квадратное уравнение имеет действительные корни и если свободный член q является положительным числом, то эти корни будут иметь одинаковый знак «+» или «-»;
- если квадратное уравнение имеет корни и если свободный член q является отрицательным числом, то один корень будет «+», а второй «-».
Оба этих утверждения являются следствием формулы x1·x2=q и правила умножения положительных и отрицательных чисел, а также чисел с разными знаками.
Являются ли корни квадратного уравнения x2−64·x−21=0 положительными?
Решение
По теореме Виета корни данного уравнения не могут быть оба положительными, так как для них должно выполняться равенство x1·x2=−21. Это невозможно при положительных x1 и x2.
Ответ: Нет
При каких значениях параметра r квадратное уравнение x2+(r+2)·x+r−1=0 будет иметь два действительных корня с разными знаками.
Решение
Начнем с того, что найдем значения каких r, при которых в уравнении будет два корня. Найдем дискриминант и посмотрим, при каких r он будет принимать положительные значения. D=(r+2)2−4·1·(r−1)=r2+4·r+4−4·r+4=r2+8. Значение выражения r2+8 положительно при любых действительных r, следовательно, дискриминант будет больше нуля при любых действительных r. Это значит, что исходное квадратное уравнение будет иметь два корня при любых действительных значениях параметра r.
Теперь посмотрим, когда корни будут иметь разные знаки. Это возможно в том случае, если их произведение будет отрицательным. Согласно теореме Виета произведение корней приведенного квадратного уравнения равно свободному члену. Значит, правильным решением будут те значения r, при которых свободный член r−1 отрицателен. Решим линейное неравенство r−1<0, получаем r<1.
Ответ: при r<1.
Формулы Виета
Существует ряд формул, которые применимы для осуществления действий с корнями и коэффициентами не только квадратных, но также кубических и других видов уравнений. Их называют формулами Виета.
Для алгебраического уравнения степени n вида a0·xn+a1·xn-1+…+an-1·x+an=0 считается, что уравнение имеет n действительных корней x1, x2, …, xn , среди которых могут быть совпадающие:
x1+x2+x3+…+xn=-a1a0,x1·x2+x1·x3+…+xn-1·xn=a2a0,x1·x2·x3+x1·x2·x4+…+xn-2·xn-1·xn=-a3a0,…x1·x2·x3·…·xn=(-1)n·ana0
Получить формулы Виета нам помогают:
- теорема о разложении многочлена на линейные множители;
- определение равных многочленов через равенство всех их соответствующих коэффициентов.
Так, многочлен a0·xn+a1·xn-1+…+an-1·x+an и его разложение на линейные множители вида a0·(x-x1)·(x-x2)·…·(x-xn) равны.
Если мы раскрываем скобки в последнем произведении и приравниваем соответствующие коэффициенты, то получаем формулы Виета. Приняв n=2, мы можем получить формулу Виета для квадратного уравнения: x1+x2=-a1a0, x1·x2=a2a0.
Формула Виета для кубического уравнения:
x1+x2+x3=-a1a0,x1·x2+x1·x3+x2·x3=a2a0,x1·x2·x3=-a3a0
Левая часть записи формул Виета содержит так называемые элементарные симметрические многочлены.
Теорема Виета .
Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с обратным знаком,
а их произведение равно свободному члену .
Приведенное квадратное уравнение это уравнение у которого (a=1 ) .
(x^2+bx+c=0 )
(x_1+x_2=-b )
(x_1 cdot x_2 =c )
Задача 1. (Теорема Виета)
Найти сумму и произведение корней квадратного уравнения:
( x^2 +4x +3=0 )
Показать ответ
Показать решение
Видеорешение
Задача 2. (Теорема Виета)
Найти сумму и произведение корней квадратного уравнения:
( x^2 +8x -20=0 )
Показать ответ
Показать решение
Видеорешение
Задача 3. (Теорема Виета)
Найти сумму и произведение корней квадратного уравнения:
( x^2 +3x -70=0 )
Показать ответ
Показать решение
Видеорешение
Задача 4. (Теорема Виета)
Найти сумму и произведение корней квадратного уравнения:
( x^2 +3x -10=0 )
Показать ответ
Показать решение
Видеорешение
Задача 5. (Теорема Виета)
Найти сумму и произведение корней квадратного уравнения:
( x^2 +15x -100=0 )
Показать ответ
Показать решение
Видеорешение
Задача 6. (Теорема Виета)
Найти сумму и произведение корней квадратного уравнения:
( x^2 -8x +15=0 )
Показать ответ
Показать решение
Видеорешение
Задача 7. (Теорема Виета)
Найти сумму и произведение корней квадратного уравнения:
( x^2 -3x +2=0 )
Показать ответ
Показать решение
Видеорешение
Задача 8. (Теорема Виета)
В уравнении (x^2+bx-35=0) один из корней равен (-5), найти второй корень и коэффициент (b)
Показать ответ
Показать решение
Видеорешение
Задача 9. (Теорема Виета)
В уравнении (x^2-13x+c=0) один из корней равен (0,5), найти второй корень и свободный член (c)
Показать ответ
Показать решение
Видеорешение
Задача 10. (Теорема Виета)
В уравнении (x^2-8x+c=0) один из корней равен (5), найти второй корень и свободный член (c)
Показать ответ
Показать решение
Видеорешение
- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Анисова Т.Л.
1
Евсеева О.А.
2
Чуев В.Ю.
1
1 Московский государственный технический университет им. Н.Э. Баумана
2 МИРЭА — Российский технологический университет
Решение задач с параметрами — одна из сложных тем курса алгебры средней школы. Задания на эту тему традиционно входят в единый государственный экзамен по математике. Однако опыт показывает, что учащиеся не всегда в достаточной мере владеют навыками решения задач с параметрами, часто допускают ошибки. В большинстве случаев это связано с неправильным выбором метода решения. Поэтому очень важно познакомить выпускников с различными подходами. Настоящая статья посвящена исследованию квадратных уравнений и сводящихся к ним систем уравнений, содержащих параметр, на некоторой области допустимых значений переменной. Подробно изложен метод решения для случаев, когда надо найти значения параметра, при которых уравнение или система уравнений имеет одно единственное решение, два различных решения или хотя бы одно решение. Установлено, что рассмотренный авторами метод решения с использованием теоремы Виета является менее затратным по сравнению с непосредственным нахождением корней, дальнейшей проверкой их попадания на область допустимых значений и последующим определением значений параметра, удовлетворяющего условию поставленной задачи. Метод позволяет избежать решения иррациональных неравенств в случае, когда дискриминант уравнения не является полным квадратом.
задачи с параметрами
математика в школе
подготовка к единому государственному экзамену (егэ)
теорема виета
1. ФГБНУ «Федеральный институт педагогических измерений». [Электронный ресурс]. URL: https://fipi.ru/ege/demoversii-specifikacii-kodifikatory#!/tab/151883967-2 (дата обращения: 17.05.2021).
2. Ященко И.В., Семенов А.В., Высоцкий И.Р. Методические рекомендации для учителей, подготовленные на основе анализа типовых ошибок участников ЕГЭ 2020 года по математике // Педагогические измерения. 2020. № 3. С.17.
3. Ледовских И.А., Горбанева Л.В., Жулидова Ю.В. Задачи с параметрами: с чего начать // Международный научно-исследовательский журнал. 2020. Вып. № 11 (101). [Электронный ресурс]. URL: https://research-journal.org/pedagogy/zadachi-s-parametrami-s-chego-nachat/ (дата обращения: 14.05.2021).
4. Мордкович А.Г. Алгебра и начала математического анализа. 10 класс. В двух частях. Ч.2: задачник (профильный уровень). М.: Мнемозина, 2020. 348 с.
5. Мордкович А.Г. Алгебра и начала математического анализа. 11 класс. В двух частях. Ч.2: задачник (профильный уровень). М.: Мнемозина, 2020. 333 с.
6. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и начала математического анализа. 11 класс. Углубленный уровень. М.: Мнемозина, 2015. 312 с.
7. Алимов Ш.А. Алгебра и начала анализа: учебник для 10-11 класса средней школы. М.: Просвещение, 2020. 463 с.
8. Колмогоров А.Н. Алгебра и начала анализа: учебник для 10-11 класса средней школы. М.: Просвещение, 2020. 320 с.
9. Галицкий М.Л. Сборник задач по алгебре для 8-9 классов: учебное пособие для учащихся школ и классов с углубленным изучением математики. М.: Просвещение, 2020. 271с.
10. Горнштейн П.И., Полонский В.Б., Якир М.С. Задачи с параметрами. М.: Илекса, Харьков: Гимназия, 2005. 328 с.
11. Шабунин М.И. Математика. Пособие для поступающих в вузы. М.: Лаборатория знаний: Лаборатория Базовых Знаний, 2016. 744 с.
12. Козко А.И., Чирский В.Г. Задачи с параметром и другие сложные задачи. М.: МЦНМО, 2007. 296 с.
13. Шахмейстер А.Х. Уравнения и неравенства с параметрами. СПб.: «Виктория плюс»: М.: МЦНМО: СПб.: «Петроглиф», 2019. 304 с.
Ежегодно в письменной части профильного единого государственного экзамена по математике выпускникам предлагается решить задачу с параметрами (задание 18) [1]. Это задание относится к высокому уровню сложности, оценивается в четыре первичных балла (максимальный балл из возможных). Согласно опубликованным данным анализа результатов ЕГЭ [2; 3], за последние пять лет видна растущая заинтересованность учащихся в правильном выполнении задания с параметрами.
Проведенный анализ школьных учебников и задачников по алгебре и началам анализа позволяет сделать следующие выводы.
В задачниках Мордковича А.Г. [4-5] и Виленкина Н.Я. [6] представлен достаточно большой объем упражнений, требующих умения применять различные методы решений заданий с параметрами. В учебнике Алимова Ш.А. [7] материал по методам решения задач с параметрами представлен незначительно. В основном рассматривается аналитический способ решения.
В учебнике Колмогорова А.Н. [8] задачи с параметрами включены в раздел «Повторение. Задачи повышенной трудности». Разобранных примеров, иллюстрирующих методы решения задач с параметрами, не приводится.
Наиболее большой спектр заданий с параметрами представлен в сборнике задач Галицкого М.Л. [9]. В нем содержатся уравнения и неравенства, системы уравнений и неравенств первого и второго порядка с параметрами, для решения которых можно применять аналитический и (или) графический методы решения. Задания располагаются в порядке повышения сложности.
В школьных учебниках практически отсутствуют объяснения решений задач с параметрами. Существует множество пособий по решению таких задач [10-13]. Заметим, что они в основном ориентированы на хорошо подготовленных учащихся, тогда как в школьных программах по математике задачам с параметрами отводится небольшое количество времени, рассматривается небольшой круг заданий.
Умение решать задачи с параметрами является одним из важнейших показателей уровня математической подготовки и глубины освоения материала. В школьной программе 8–11 классов задачи с параметрами обычно рассматриваются в конце каждой темы, что позволяет учащимся обобщать и структурировать полученные знания. Решение задач с параметрами развивает способность анализировать и формирует навыки логического мышления.
Нужно отметить, что задачи, содержащие параметр, очень разнообразны, и при их решении используются различные методы (графический, аналитический, перебор вариантов, комбинированный и т.д.). Наибольшую трудность для учащихся как раз составляет выбор «правильного» метода, позволяющего обоснованно и с наименьшими затратами выполнить решение задачи.
Цель исследования: показать необходимость изучения школьниками метода, основанного на применении теоремы Виета, для решения систем уравнений с параметрами, сводящихся к квадратному уравнению. При этом на область допустимых значений переменной (ОДЗ) накладывается определенное условие, определяемое из условия задачи.
Материал и методы исследования. Рассмотрим следующую задачу. Дана система уравнений, которая сводится к квадратному уравнению вида
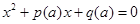
содержащему параметр 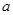
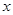
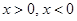
либо 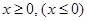
Дискриминант уравнения равен 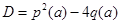
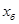
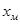
Зачастую учащиеся пытаются непосредственно найти решения уравнения (1) и определить, при каких значениях параметра 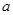
Если требуется найти значения параметра 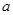
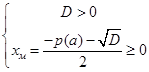
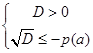
Если требуется найти значения параметра 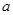
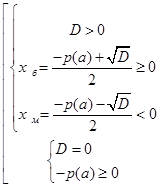
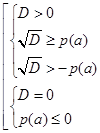
Если же для уравнения (1) с ОДЗ (3) требуется найти значения параметра 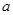
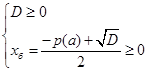
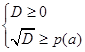
В том случае, когда дискриминант уравнения (1) является полным квадратом, решение систем (4), (6) либо совокупности (5) не вызывает у выпускников трудностей. В противном случае само по себе решение иррациональных неравенств – сложная задача, ведь каждое из этих неравенств, в свою очередь, сводится к решению системы неравенств и приводит чаще всего к ряду ошибок.
Для уравнения (1) при ОДЗ 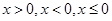
В пособиях [10; 12] для решения рассматриваемого класса задач используется графический метод, основанный на исследовании расположения корней квадратного трехчлена относительно нуля. Этот метод больше подходит учащимся с развитым визуальным восприятием.
Использование теоремы Виета подойдет учащимся, склонным к аналитическому мышлению. Предлагаемый метод позволяет, на наш взгляд, существенно упростить решение рассматриваемой задачи, избежав решения иррациональных неравенств.
Пусть дано квадратное уравнение
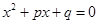
его дискриминант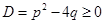


Соответствие между корнями квадратного уравнения и его коэффициентами
|
|
|
|
|
|
|
|
|
|
|
|
Естественно, данная таблица не подлежит заучиванию. Учащимся необходимо объяснить механизм приведенных соответствий, следующих из теоремы Виета.
Используя соответствия, представленные в таблице, при решении выше поставленной задачи приходим к системам, не содержащим иррациональных неравенств.
Если требуется найти значения параметра 
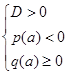
Для нахождения значений параметра 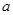
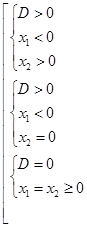
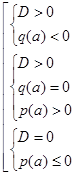
Для нахождения значений параметра 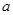
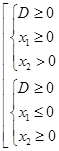
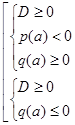
Уравнение (1) при ОДЗ 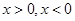
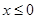
Рассмотрим следующие примеры.
Пример 1. Найти значения параметра 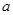
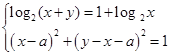
имеет а) два различных решения; б) единственное решение; в) хотя бы одно решение.
Решение. Из первого уравнения получаем
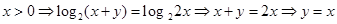
Поскольку для каждого значения переменной 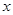
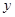
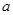
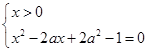
а) Система (8) имеет два различных решения при
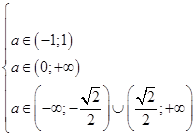
Окончательно, 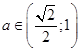
б) Система (8) имеет единственное решение при
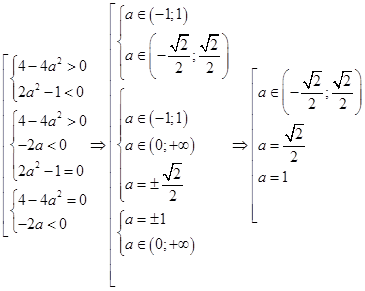
Окончательно, 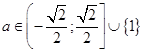
в) Система (8) имеет хотя бы одно решение при
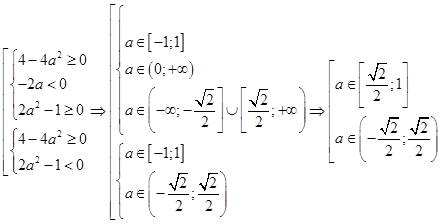
Окончательно, 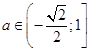
Находя корни квадратного уравнения непосредственно, имеем
содержащую иррациональное неравенство.
Пример 2. Найти значения параметра 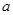
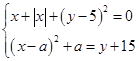
имеет
а) два различных решения; б) единственное решение; в) хотя бы одно решение.
Решение. Поскольку при 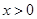
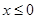
и второе уравнение имеет вид
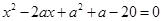
Задача свелась к нахождению числа решений системы
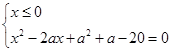
в зависимости от параметра 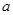
а) Система (10) имеет два различных решения, если
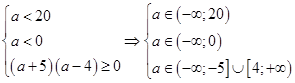
Окончательно, 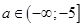
б) Система (10) имеет единственное решение при
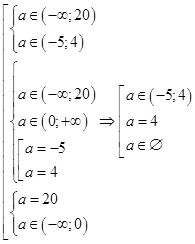
Окончательно, 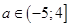
в) Система (10) имеет хотя бы одно решение при
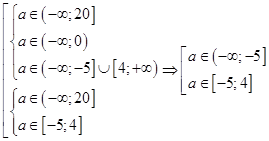
Окончательно, 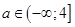
Заключение. Предложенный в статье метод решения задач достаточно легко усваивается учащимися. Навык использования теоремы Виета быстро развивается. Такой способ решения подойдет учащимся, склонным к аналитическому мышлению. Отметим, что важно познакомить выпускников со всеми методами решения задач с параметрами, поскольку зачастую при решении таких задач используется комбинированный подход.
Приведенные примеры иллюстрируют преимущество данного метода по сравнению с непосредственным нахождением корней, дальнейшей проверкой их попадания на ОДЗ и последующим определением значений параметра, удовлетворяющих условию поставленной задачи. При использовании данного метода, в отличие от стандартного метода, отпадает необходимость решения одного или нескольких иррациональных неравенств.
Библиографическая ссылка
Анисова Т.Л., Евсеева О.А., Чуев В.Ю. ПРИМЕНЕНИЕ ТЕОРЕМЫ ВИЕТА К РЕШЕНИЮ НЕКОТОРЫХ ЗАДАЧ С ПАРАМЕТРАМИ // Современные проблемы науки и образования. – 2021. – № 3.
;
URL: https://science-education.ru/ru/article/view?id=30869 (дата обращения: 01.04.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
МЕТОДИЧЕСКАЯ НАУКА — УЧИТЕЛЮ МАТЕМАТИКИ
УДК 373.5.016:51
О ТЕОРЕМЕ ВИЕТА, УРАВНЕНИЯХ КВАДРАТНЫХ И НЕ ТОЛЬКО
Трегуб Нина Леонидовна,
учитель
e-mail: nina.tregub@mail.ru МОУ «Гимназия № 70 г. Донецка», г. Донецк
Tregub Nina, Teacher
Gymnasium number 70, Donetsk
В статье описываются примеры использования теоремы Виета для широкого класса задач с целью расширения методического кругозора молодых учителей математики. Авторский подход к применению теоремы Виета даст возможность познакомить с такими методами решения задач учащихся, в особенности тех, кто готовится к поступлению в высшие учебные заведения, кто интересуется математикой и хочет участвовать в олимпиадах разных уровней.
Ключевые слова: теорема Виета, методы решения нестандартных задач, подготовка учащихся к математическим олимпиадам.
Постановка проблемы. Как свидетельствует авторский многолетний опыт, большинство учителей к сути квадратных уравнений, уравнений высших степеней и к использованию теоремы Виета для квадратных и других алгебраических уравнений относится достаточно «прагматично», то есть используют их очень редко и в совсем простых заданиях. Чаще всего это именно такие традиционные задания, где прямо сказано «использовать теорему Виета» или просто речь идет о сумме и произведении корней (причем только квадратного уравнения).
Увидеть «спрятанную» теорему Виета и тем самым найти короткий и красивый способ решения задачи не так легко, если решающий не имеет определенных навыков. Использование данной теоремы в нестандартных задачах требует наличия семантической гибкости мышления и способствует развитию творческих способностей учащихся.
Цель статьи — показать авторский подход к применению теоремы Виета для решения нестандартных математических задач, позволяющий расширить методический кругозор молодому учителю математики.
Изложение основного материала. Вначале несколько слов хотелось бы сказать об уравнениях вида
ах2 + Ьх + с = 0 , (1)
которые далеко не всегда являются квадратными. Очевидно, что при а = 0 уравнение становится линейным, а при а = Ъ = с = 0 превращается в тождество. Решая задания с параметром, учащиеся часто забывают о таких фактах; то есть на вопрос, когда уравнение вида (1) имеет один корень, тут же отвечают: «Когда дискриминант равен нулю», забывая рассмотреть случай линейного уравнения.
Задание 1. (см. [4]) При каких значениях параметра а уравнение (а + 1)х2 -(4а + 6)х + а + 9 = 0 (2)
имеет единственное решение?
Легко проверяется, что при а = — 1 уравнение (2) становится линейным и имеет один корень. При а ф —1 уравнение (2) будет квадратным и тогда решение будет единственным в случае, когда дискриминант равен нулю. В этом случае, а будет равняться —2/3 или 0.
Таким образом, исходное уравнение (2) будет иметь единственное решение при а, равном —1; —2/3 ; 0.
Остановимся теперь на следующем факте.
Утверждение. Если уравнение ах2 + Ьх + с = 0 имеет три различных корня (то есть функция
f(x) = ах2 + Ьх + с имеет нули в трех различных точках), то а = Ь = с = 0. (Это нетрудно доказать).
Следствием этого факта может быть такое утверждение: «Если уравнение f(x) = М, где f(x) = ах2 + Ьх + с, а М = const, имеет три разных корня, то fipc) = М при всех действительных значениях х, то есть равенство fipc) тождественно равно М».
Таким образом, а = Ь = 0, с = М.
Примерами использования приведенного факта будут небезызвестные задания. (См., например, [1], [2], [5], [6]).
Задание 2. Найдите значение выражения
(.х — а)(х — Ь) (х — Ь)(х — с)
(с — а)(с — Ь) (а — Ь)(а — с) (х — с)(х — а)
(Ь — с)(Ь — а). Задание 3. Докажите тождества:
(х—а)(х—Ь) (х—Ь)(х—с)
а) (с—а)(с—Ь) + (а—Ь)(а—с) + (х — с) (х — а)
+Ь(Ь — с)(Ь — а) =х;
2 (х—а)(х—Ь) 2 (х— Ь)(х— с) ) (с—а)(с—Ь) + (а—Ь)(а—с) + 2(х — С)(х — а) 2
+Ь2-= х2.
(Ь — с)( Ь — а)
Начнем с задания 2. Очевидно, что функция
, _(х а)(х — Ь) (х — Ь)(х — с)
‘(Х) = (с — а)(с — Ь) + (а — Ь)(а — с) + (х с)(х—а)
(Ь—с )(Ь—а ) имеет степень не выше второй. Кроме того, легко увидеть, что
f( а) = f( Ь) = f( ) = 1.
Поэтому в соответствии с выше приведенным утверждением /(х) = 1 при всех действительных значениях х.
Что касается задания 3 а), то, чтобы доказать это тождество, введем функцию *— п (х-а)(х-Ь) , (х-Ь)(х-с)
/(х) ~а (с-а)(с-Ь) + ° (а—Ъ)(а—с) + (х — с)(х — а)
+с—х
(Ъ — с)( Ъ — а) » Степень этой функции также не выше второй. Убедимся, что /(а) = /(Ъ) = /(с) = 0. Поэтому /(х) = 0 при всех действительных значениях х, то есть тождество доказано. Аналогично доказывается и тождество 3б). Только для его доказательства необходимо ввести функцию (х — а) (х — Ъ)
f( х) = 2
+а
+Ь
(с — а) (с — Ь)
(х — Ь)(х — с) 2—+
(а — Ь)(а — с) ( х — )( х — а)
(Ь — с)( Ь — а)
+
х
и убедиться, что
/(а) = /(Ъ) = /(с) = 0.
Задание 4. Пусть а, Ь, с — различные числа. Докажите, что из системы гх + ау + а2 г = 0; х + Ъу + Ъ2х = 0; х + су + с2г = 0
следуют равенства х = у = z = 0.
Для решения этой задачи введем функцию /(1) = г 12 + у1 + х. (3)
Тогда по условию
/ (а) = х + ау + а2 г = 0; < /(Ь) = х + Ьу + Ь2г = 0; / (с) = х + су + с2 г = 0.
Функция (3) имеет три нуля. Это означает, что в уравнении
г г2 + уг + х = 0 все коэффициенты равны нулю, то есть 2 = у = х = 0, что и требовалось доказать.
Приведем теперь примеры заданий, для решения которых может быть использована теорема Виета.
Задание 5. Известно, что
х + у = а + Ъ, х2 + у2 = а2 + Ъ2 .
Докажите, что при любом натуральном п выполняется равенство
(86)
хп + у11 = ап + Ьп. Доказательство начнем с очевидного факта: если х + у = а + Ь, то (х + у)2 = (а + Ъ)2. Тогда ху = аЬ, так как по условию х2 + у2 = а2 + Ъ2 .
Обозначим х + у = а + Ъ = —т, ху = аЬ = п.
Рассмотрим уравнение
г2 + тС + п = 0 . (4)
Уравнение (4) имеет только 2 корня ^ и 12 . По теореме Виета выполняется
Н + ь2 = —т, ь2 = п.
Тогда или х = а, у = Ь, или х = Ь, у = а. Очевидно, что в этих обоих случаях выполняется
хп +уп = ап + Ьп, что и требовалось доказать.
Аналогичная идея лежит в основе решения следующего задания.
Задание 6. Существуют ли 4 различных положительных числа х, у, а, Ь таких, что
х + у = а + Ь, х3 + у3 = а3 + Ъ3 ? Пусть такие 4 числа существуют, причем эти числа различные. Тогда из формул (х + у)(х2 — ху + х2) =
= (а + Ь)(а2 — аЬ + Ъ2) , учитывая, что все числа положительные, то есть х + у = а + Ъ ф 0, получаем: х2 — ху + у2 = а2 — аЬ + Ь2. Отсюда
(х + у)2 — 3ху = (а + Ь)2 — 3аЬ , значит, ху = аЬ.
Проведем рассуждения, аналогичные рассуждениям задания 4. Пусть х + у = а + Ъ = —т, ху = аЬ = п.
По теореме, обратной теореме Виета, х и у , а также а и Ь — корни квадратного уравнения (4). Но это уравнение не может иметь более двух корней, то есть множества этих корней совпадают, вследствие чего различных четырех положительных чисел, удовлетворяющих условию, не существует.
Задание 7. При каких значениях а четыре корня уравнения
х4 + (а — 5)х2 + (а + 2)2 = 0 (5) являются последовательными членами арифметической прогрессии?
Обратим внимание на то, что данное уравнение биквадратное. Обозначим х = I. Получим уравнение
г2 + (а — 5^ + (а + 2)2 = 0……(6)
По теореме Виета для уравнения (6)
Ь1 + Ъ2 = —(а — 5),
^г2 = (а + 2)2. >0; г2> 0. Пусть для определенности ^ > ^ .
Тогда корни уравнения (5) имеют вид ^1; 2; ^2; Так как по усло-
вию в указанном порядке эти корни образуют арифметическую прогрессию, то
t? —
Отсюда = то есть ^ = 9t2.
Подставив данное равенство в соотношения между корнями (теорему Виета), получаем, что
7 7 5
t2 = h =9 •— при а = — —
13
и t2 — 1, t1 — 9 • при а — -5.
13
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Таким образом, корни уравнения (5) являются последовательными членами
арифметической прогрессии при а = —и
и при а = —5.
Приведем теперь теорему Виета для уравнений п — ой степени.
Обобщенная теорема Виета: Пусть х1, х2, …, хп — корни многочлена
1 х + 2Х + •••
+ а1 х + а0(ап ф 0). Тогда справедливы равенства
Х1 + Х2 + •■■ + Х-^ — ;
Х1 х2 + Х1 х3 + •» хп—1 хп = ап—2/ап;
Xi • %2 • *шш • ^^ —
(-1Уа0
Для приведенного уравнения третьей степени вида
х3 + ах2 + Ъ х + с = 0 по теореме Виета
Х1 + Х2 + Х3 = — а, Х1 х2 + Х1 х3 + х2х3 = ^, Х1Х2Х3 = ^ ,
где Х1, х2х.3 — корни уравнения.
Соответствующие равенства можно записать и для уравнения четвертой степени.
Задание 8. Определите все значения а, при каждом из которых три различных корня уравнения
х3 + (а2 — 9а)х2 + 8а х — 64 = 0 (7) образуют геометрическую прогрессию. Найдите эти корни.
Запишем теорему Виета для корней Х1, Х2, Х3 уравнения (7):
(87)
х1 + х2 + х3 = — (а2 — 9а), х1х2 + х1х3 + х2х3 = 8а,х1х2х3 = 64.
Так как корни уравнения (7) образуют
геометрическую прогрессию, то выполня-
2
ется условие х2 = х1 • хз.
Тогда из равенства х1х2х3 = 64 следует, что х23 =64, откуда х2 = 4. Подставив данное значение корня в уравнение (7), получаем, что а = 0 или а = 7. Но при а = 0 уравнение (7) имеет лишь один действительный корень.
Далее можно подставить значение а = 7 в исходное уравнение и, зная, что один из корней равен 4, по схеме Горнера или делением многочлена на многочлен, прийти к квадратному уравнению х2 — 10х + 16 = 0.
Оставшиеся два корня равны 2 и 8.
Это же квадратное уравнение для оставшихся корней можно получить из соотношений теоремы Виета, подставив в соответствующие равенства а = 7; х2 = 4. (х1 + х2 = 10; х1х2 = 16).
Итак, корни образуют геометрическую прогрессию и равны 2, 4, 8 при а = 7.
Задание 9. Решите систему уравнений:
х + у + z = 2;
(8)
а) ху + уг + 1х = —5; хух = —6.
х + у + 2 = 1;
б) {ху + уг + гх = —4; (9)
х3 + у3 + г3 = 1. Для решения системы (8) обратим внимание на то, что по теореме, обратной теореме Виета, х, у и г — корни следующего кубического уравнения
г3 — 2г2 — 5 г+ 6 = 0, которые равны Ь2 = —2^1 = 1^3 = 3 . Поэтому решения этой системы (—2; 1; 3), (—2; 3; 1), (1; 3; —2), (1; —2; 3), (3; —2;1), (3; 1; —2).
Чтобы решить систему (9) используем формулу
(х + у + г)3 = х3 + у3 + г3 + +3(х + у + г)(ху + уг + гх) — 3хуг …. (10) и получим, что хуг = —4. Тогда по теореме, обратной теореме Виета, х, у и г -корни уравнения ^ — ^ — 41 + 4 = 0. Дальнейшее решение системы очевидно.
Задание 10. Известно, что х + у + = а + Ъ + ; 1 ху + ух + гх = аЪ + Ъс + са;
х3 + у3 + 3 = а3 + Ъ3 + 3.
Докажите, что при любом натуральном n выполняется равенство
хп + уп +zn = ап +Ьп +сп.
Для доказательства обозначим х + у + z = А, ху + yz + zx = В. Используя формулу (10), получаем: xyz = abc. Обозначим xyz = abc = С. Рассмотрим уравнение
t3 — Аt2 + Bt — С = 0. Это уравнение имеет не более трех корней. Но x, y, z и a, b, c — соответствующие корни этого уравнения, поэтому множества корней этого уравнения совпадают, то есть
хп + уп + zn = ап +Ьп + сп при любом натуральном п.
Задание 11. Числа x , y , z удовлетворяют системе
<х + у + z = а,
1+1+1—1
x у z а
(11)
Докажите, что хотя бы одно из этих чисел равняется а.
Если привести второе равенство системы (11) к общему знаменателю, то получим, что хуг = а(ху + уz + гх). Обозначим хуг = т; ху + ух + гх = р. Тогда т = ар. По теореме, обратной теореме Виета, х, у и г — корни следующего уравнения третьей степени
13 — а 12 + рЬ — т = 0.
Учитывая, что т = ар, получаем, что наше уравнение преобразуется к виду (t — а2 + р) = 0. Очевидно, что один из корней этого уравнения = а, поэтому хотя бы одно из чисел х , у , г равняется а.
Задание 12. Решить систему г г + ау + а2х + а3 = 0, г + Ъу + Ъ2х + Ъ3 = 0, 2 + су + с2х + С3 = 0.
Рассмотрим многочлен Р( t) =t3 +xt2 + уг +z,
(12)
(13)
который имеет не более трех корней. Но согласно системе (12) P(b) = Р(с) = 0. Тогда a, b, c — корни (13). Поэтому по теореме Виета для многочлена (13). а + b + с = —х; ab + bc + са = у; аЬс = —z. Тогда решение системы (12): х = —(а + b + с); у = ab + bc + са; z = —abc. Задание 13. Один из корней уравнения с целыми коэффициентами
®
х4 + ах2 + Ъх + 2 = 0 (14) равен 1 — V2. Найти а, Ь и остальные корни.
Рассмотрим несколько способов решения этого задания.
Но вначале заметим, что если уравнение имеет целые коэффициенты, то иррациональные корни этого уравнения будут сопряженными, то есть
х1 = 1 — V2, х2 = 1 + VI. Тогда х1 + х2 =2; х1 х2 = —1. Способ 1. По теореме, обратной теореме Виета, х1 и х2 — корни квадратного трехчлена х2 — 2х — 1, а многочлен в левой части уравнения (14) делится на этот трехчлен нацело, при этом частное равно
х2 +2х — 2, (15)
откуда получаем а = —7; Ъ = 2.
Приравняв (15) к нулю получаем, что х3,4 = 1 ±
Способ 2. Проводя рассуждения, аналогичные рассуждениям способа 1, учтем, что многочлен х4 + ах2 + Ъх + 2 делится на х2 — 2х — 1. Используем метод неопределенных коэффициентов. Запишем х4 + ах2 + Ъх + 2 = = (х2 — 2х — 1)(х2 + сх — 2). После раскрытия скобок получаем, что а = —7; Ъ = 2; с = 2.
Способ 3. Используем теорему Виета для уравнения четвертой степени (14).
Х1 + Х2 + Х3 + Х4 = 0, Х1 + Х2 =2;
тогда х3 + х4 = —2.
х1 х2 = —1, х1 х2 х3 х4 = 2, потому
Х3 Х4 = 2.
По теореме Виета
а = Х1Х2 + Х1Х3 + Х1Х4 + Х2 Х3 + +Х2 Х4 + Х3 Х4 =
= — 1 + х1 (х3 + х4) + х2 (х3 + х4) + (—2) = = —3 + (Х1 + Х2 )(Х3 + Х4) = —7.
Ъ = Хц Х2 Х3 + ХцХ2 Х4 + ХцХ3 Х4 + Х2 Х3 Х4 =
— Хц Х2 (х3 + х4) + х3х4 + Х2) — 2.
По теореме, обратной теореме Виета, х3 и х4 — корни квадратного уравнения х2 +2х — 2 = 0, откуда мы и находим х3 и х4.
Все приведенные выше задания -только малая часть примеров, с помощью которых можно привлечь внимание учителей к использованию такой яркой и красивой теоремы, как теорема Виета. Считаю, что эта небольшая статья будет полезна учителям, работающим в классах математического профиля, классах с углубленным изучением математики и учителям, готовящим учащихся к ГИА, ЕГЭ и ВНО и олимпиадам разных уровней.
1. Алфутова Н.Б. Алгебра и теория чисел. Сб. задач для математических школ / Н.Б. Алфутова, А.В. Устинов. — 3-е изд., испр. и доп. — Москва: МЦНМО, 2009. — 336 с.
2. Дорофеев Г.В. Многочлены с одной переменной. Книга для учащихся /Г.В. Дорофеев, С. В. Пчелинцев. — Москва : Просвещение, 2001. -140 с.
3. Козко А.И. ЕГЭ 2010. Математика. Задача С5 / А.И. Козко и др. — М. : МЦНМО, 2010. -127 с.
4. Математика. Пособие для поступающих в десятый лицейский класс: Варианты вступительных заданий : Учеб. пособие / Сост. Л.А. Приходько; Под общей ред. Проф. В.Я. Райцина. — Москва : Изд-во «Экзамен», 2006. -146 с.
5. Мерзляк А.Г. Алгебра. Учебник для 8 кл. с углуб. изучением математики / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. -Харьков : Гимназия, 2016. — 384 с.
6. Мерзляк А.Г. Алгебра и начала анализа. Учебник для 10 класса с углубленным изучением математики / А.Г. Мерзляк, Д.А. Номи-ровский, В.Б. Полонский, М.С. Якир. — Харьков: Гимназия, 2010. — 415 с.
Abstract. Tregub N. ON THE THEORY OF VEET, EQUATIONS OF SQUARE AND NOT
ONLY. The article describes examples of using the Vieta theorem for a wide class of problems with the purpose of expanding the methodological outlook of young mathematics teachers. The author’s approach to the application of Vieta’s theorem will provide an opportunity to acquaint students with such methods of solving problems, especially those who are preparing to enter higher education institutions, who are interested in mathematics and want to participate in Olympiads of different levels.
Key words: Vieta’s theorem, methods for solving non-standard problems, preparing students for mathematical Olympiads.
Статья представлена профессором Вит.В. Волчковым.
Поступила в редакцию 19.03.2018 г.
®
Общие сведения
Для применения формул теоремы Виета для квадратного уравнения следует разобрать некоторые термины и математические определения. Квадратным уравнением вида Am2 + Bm + C = 0 называется многочлен второй степени, состоящий из коэффициента А при некоторой неизвестной в квадрате и суммы произведения второго коэффициента на неизвестную величину и константы С. Этот многочлен преобразовывается в уравнение только при равенстве нулевому значению. Константу С еще называют свободным членом.
Корнями называются такие значения неизвестных, при подстановке которых тождество считается верным. Следует отметить, что в результате отдельных математических преобразований появляются дополнительные корни. Особенно это касается различных замен в тригонометрических функциях. Однако при подстановке корней равенство не соблюдается. Математики называют их ложными. После решения уравнения специалисты рекомендуют произвести подстановку этих значений в исходное уравнение. Этот прием помогает избавиться от нежелательных решений.
Поиск корней при помощи теоремы Виета принадлежит к быстрым методикам, поскольку избавляет человека от ненужных расчетов по формулам с применением дискриминанта.
Виды квадратных уравнений
Квадратные уравнения бывают нескольких видов, поскольку не во всех случаях коэффициенты получаются отличными от нуля. Математики классифицировали их на 2 типа:
- полные;
- неполные.
Первыми называются выражения со всеми коэффициентами (A, B и C), отличными от нуля. Если число перед неизвестной не указано, то считается, что оно эквивалентно 1. Неполными считаются любые уравнения, в которых отсутствует B или C. Однако бывают случаи, когда оба последних коэффициента соответствуют нулю, тогда тождество имеет следующий вид: Am2 = 0. Кроме того, существует еще один критерий распределения на виды, основанный на степени приведенности. По этому признаку выражения делятся на приведенные и неприведенные классы.
К первым следует отнести любые равенства, у которых коэффициент равен 1. Во всех остальных случаях (А > 1) тождества являются неприведенными.
Условие использования закона
Закон Виета применим не ко всем уравнениям. Математики сформулировали важные условия, при соблюдении которых возможно воспользоваться этим правилом: уравнение должно быть приведенным и иметь значение дискриминанта больше 0. Из этого условия можно сделать вывод: когда равенство невозможно преобразовать к приведенному, следует применять другие методики нахождения корней, а не правило Виета.
Существует простой алгоритм преобразования уравнения к необходимому виду. Для этого нужно выполнить несложную операцию деления каждого коэффициента на А. Например, следует преобразовать уравнение 4p2 + 8p + 16 = 0 в приведенное. Следуя описанному алгоритму, получается такое соотношение: [(4p2) / 4] + [8p / 4] + [16 / 4] = 4p2 + 2p + 4 = 0.
Специалисты рекомендуют избегать ситуаций получения обыкновенных дробей в результате преобразования. Примером является тождество 3p2 + 2p — 4 = 0. Его можно свести к приведенному, но применить теорему будет весьма сложно, поскольку равенство будет иметь такой вид: p2 + (2p / 3) — (4 / 3) = 0. Рекомендуется решать такие уравнения, используя другие методики (построение графика функции, при помощи программ или по формуле дискриминанта).
Применение теоремы
Формулировка закона Виета для квадратного уравнения Am2 + Bm + C = 0 следующая: сумма корней соответствует коэффициенту А, взятому с противоположным знаком, а результат произведения эквивалентен свободному члену С. Решение осуществляется методом подбора соответствующих числовых значений. Однако каждая теорема должна доказываться.
Чтобы осуществить эту операцию, нужно воспользоваться специальными формулами корней, используя дискриминант. Нужно предположить, что для уравнения Am2 + Bm + C = 0 справедливы два равенства: m1 + m2 = -B и m1 * m2 = C. Выражая значения корней через дискриминант в обобщенном виде, можно получить такие тождества:
- m1 = [-B — D^(½)] / (2 * A).
- m2 = [-B + D^(½)] / (2 * A).
Далее нужно найти сумму m1 и m2: [-B — D^(½)] / (2 * A) + [-B + D^(½)] / (2 * A). Чтобы упростить полученное выражение, следует воспользоваться таким алгоритмом:
- Привести дроби к общему знаменателю: [(-B — D^(½)) + (-B + D^(½))]/(2 * А).
- Упростить выражение (разложение на множители): [-B — D^(½) — B + D^(½)]/(2 * А) = (-2B) / (2 * A) = — B / A = -B / 1 (А = 1).
После этого нужно доказать, что произведение корней эквивалентно С. Для этого необходимо перемножить m1 = [-B — D^(½)] / (2 * A) и m2 = [-B + D^(½)] / (2 * A), воспользовавшись правилом умножения дробей обыкновенного типа по такой методике:
- Перемножить числители и знаменатели: [-B — D^(½)] / (2 * A) * [-B + D^(½)] / (2 * A) = [(-B + D^(½)) * (-B — D^(½))] / (4 * A2).
- Упростить: [B2 — D] / 4A2 = [B 2 — (-B2 — 4 * A * C)] / 4A2 = (B2 — B2 + 4 * C) / 4 = C (при А = 1).
Вторая формула доказана. Однако перед решением обязательно следует вычислить значение дискриминанта, поскольку при D = 0 уравнение имеет только один корень. Существует обратная теорема Виета. У нее такая формулировка: если сумма чисел m1 и m2 соответствует некоторому значению В, взятому с противоположным знаком, а также их произведение эквивалентно свободному члену многочлена второй степени, значит, они являются корнями Аm 2 + Bm + C = 0. Это утверждение имеет доказательство, для которого следует выполнить следующие шаги:
- Подставить m1 и m2 в исходное уравнение: m2 — (m1 + m2) * m + m1 * m2 = 0.
- Раскрыть скобки и привести подобные слагаемые: m2 — (m1 * m — m2 * m + m1 * m2 = (m — m1) * (m — m2) = 0.
- Найти корни тождества в пункте 2: m = m1 и m = m2.
Следовательно, теорема доказана, поскольку числа m1 и m2 являются корнями уравнения. Далее нужно рассмотреть приведенные кубические уравнения и порядок применения утверждения Виета.
Кубические равенства с неизвестным
Можно также применять теорему Виета для кубического уравнения вида А * m3 + B * m2 + C * m + D = 0. Коэффициент А должен быть равен 1. Находятся корни при помощи перебора значений, но сделать это сложно, поскольку необходимо решить систему, состоящую из трех равенств:
- m1 + m2 + m3 = -B.
- m1 * m2 + m1 * m3 + m2 * m3 = C.
- m1 * m2 * m3 = -D.
Числа m1, m2 и m3 являются корнями. Кроме того, следует обратить внимание на образование ложных результатов, поскольку уравнение является кубическим. Ученые пришли к выводу о том, что чем выше степень, тем больше образовывается ложных ответов. Они рекомендуют применять специальное программное обеспечение для поиска решения. Если его нет под рукой, то можно построить график функции, а затем найти точки пересечения с осью абсцисс. Существуют также специализированные веб-сервисы. Они называются онлайн-калькуляторами.
Примеры решения
Несмотря на простоту теоремы, существует несколько типов упражнений на эту тему. Они делятся на следующие классы:
- простые;
- средние;
- продвинутые;
- сложные.
К первым следует отнести задачи на простой подбор корней. Средними считаются задания на преобразование квадратного уравнения к приведенному.
Продвинутыми являются любые тождества, которые необходимо упростить и привести к коэффициенту А = 1. Сложные — особый вид. Для них следует применить все знания в области математики. Кроме того, нужно осуществить объяснение хода решения. В некоторых случаях необходимо построить таблицу зависимостей и начертить график.
Интересный факт заключается в том, что именно этот класс выражений существенно развивает умственные способности человека на уроках. Встречаются также задачи на пересечения параболы и прямой, которая может проходить под определенным углом. Далее нужно разобрать практическое применение теоремы Виета на примерах с решением для различных классов задач.
Простой и средний
Пусть дано тождество m2 — 5 * m + 6 = 0. Необходимо найти его корни. Для решения следует применить такой алгоритм:
- Найти дискриминант: D = (-5)^2 — 4 * 1 * 6 = 1 (два корня, поскольку D > 0).
- Методом перебора можно получить решения m1 = 2 и m2 = 3.
- Проверка I корня: 22 — 5 * 2 + 6 = 4 — 10 + 6 = 0 (соответствует).
- Подстановка для II: 32 — 5 * 3 + 6 = 9 — 15 + 6 = 0 (соответствует).
Следовательно, тождество решено верно. Далее можно рассмотреть средний тип упражнения. Для этого следует решить уравнение 3 * m2 + 33 * m + 30 = 0. Найти корни можно по такому алгоритму:
- Преобразование к приведенному (разделить на А = 3): 3 * m2 + 33 * m + 30 = m2 + 11 * m + 10 = 0.
- Найти D: D = 121 — 4 * 10 = 81 > 0 (два).
- Корни: m1 = -10 и m2 = -1.
- Проверка: (-10)^2 + 11 * (-10) + 10 = 100 — 110 + 10 = 0 и (-1)^2 + 11 * (-1) + 10 = 1 — 11 + 10 = 0.
Следовательно, корни m1 и m2 удовлетворяют этому уравнению. Если не получается делить все члены на А, то необходимо рассмотреть решение с помощью дискриминанта или графическим методом.
Продвинутый класс
Для иллюстрации этого вида нужно решить следующее тождество: (m — 4)^2 — 20 = -m (m — 8) + 14. Следует воспользоваться инструкцией такого вида:
- Раскрыть скобки: m2 — 8 * m + 16 — 20 = -m2 + 8 * m + 14.
- Перенести все слагаемые в левую часть и упростить: 2 * m2 — 16 * m — 18 = 0.
- Сократить на 2: m2 — 8 * m — 9 = 0.
- Найти значение D: D = 64 + 36 = 100 > 0 (2).
- Вычисление корней: m1 = -1 и m2 = 9.
- Проверка: (-1)^2 — 8 * (-1) — 9 = 1 + 8 — 9 = 0 и 92 — 8 * 9 — 9 = 81 — 72 — 9 = 0.
На основании шестого пункта можно сделать вывод, что корни подобраны правильно. Этот пример показывает, что одной теоремы недостаточно, поскольку следует уметь выполнять математическое преобразование заданного выражения. В этом классе примеров возможен случай, когда величина дискриминанта эквивалентна 0. Следовательно, у тождества с неизвестным всего один корень. К последнему невозможно применить закон Виета.
Сложные упражнения
Примером сложной задачи, которую еще называют «со звездочкой», является следующая: необходимо найти сумму, произведение и сумму квадратов решений уравнения m 2 — 7 * m + 12 = 0, не находя корней. По обычной методике нужно доказать, что у выражения с неизвестным существует два корня по формуле дискриминанта: D = 49 — 4 * 12 = 1 > 0. Следовательно, ориентируясь на последнее равенство, условие соблюдается. По теореме Виета получаются ответы на первые два вопроса:
- m1 + m2 = 7.
- m1 * m2 = 12.
Затем следует записать сумму квадратов, используя две описанные выше формулы: (m1)^2 + (m2)^2 = (m1)^2 + (m2)^2 — 2 * m1 * m2 — 2 * m1 * m2 = (m1 + m2)^2 — 2 * m1 * m2 = 7 2 — 2 * 12 = 25. Задача решена: 7; 12 и 25.
Следующий пример является довольно распространенным. Существует уравнение 5 * m 2 — 15 * m + 30 = 0. Необходимо найти сумму кубов корней и квадрат разности. Многие ученики на протяжении всей истории существования алгебры делают однотипную ошибку. Она заключается в подготовке, то есть записываются соответствующие формулы сокращенного умножения. Если их не знают, то пользуются интернетом или другими источниками. На эту операцию тратится драгоценное время. Чтобы этого избежать, необходимо воспользоваться таким алгоритмом:
- Сократить на общий множитель, равный 5: m2 — 3 * m + 10 = 0.
- Вычислить величину дискриминанта: D = 9 — 4 * 1 * 10 = -31 < 0.
Следовательно, у равенства с неизвестными корней нет вообще. В результате невозможно найти необходимые значения. Этот прием лишний раз показывает, что можно избежать множества ошибок и не тратить время, пользуясь соответствующим алгоритмом.
Решение квадратных и кубических приведенных уравнений осуществляется при помощи соотношения Виета. Однако важным аспектом при осуществлении этой операции является нахождение величины дискриминанта.