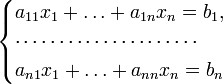Realurix теорема об эквивалентности

ТЕОРЕМА ОБ ЭКВИВАЛЕНТНОСТИ
ИНЕРТНОЙ И ГРАВИТАЦИОННОЙ МАСС

• Автор категорически запрещает использовать изложенное
  для нанесения ущерба кому бы то ни было.

• Копирование статьи для перепечатки и распространения
  возможны исключительно с разрешения автора.

• Если изложенное помогло найти решение какой-то задачи,
  то ссылка на автора и статью обязательны.

Цель работы — демонстрация обнаруженного Автором нарушения Закона Сохранения Энергии ныне действующими воззрениями на гравитацию как искривление пространства-времени и предложение такой физической модели гравитации, которая устраняет обнаруженное нарушение Закона Сохранения Энергии. Работа посвящена физике, поэтому все объёмные математические выкладки желающие могут повторить самостоятельно.

Энергия — свойство объектов материального мира, скалярная и всегда положительная величина. Энергия в материальном мире не может существовать самостоятельно без объекта-носителя. Носителями энергии являются как частицы, так и поля. Энергия никуда не исчезает и из ниоткуда не появляется. Носители энергии могут передавать энергию друг другу, при этом суммарно количество энергии и количество движения (импульс) взаимодействующих объектов всегда остаётся неизменным. Переносящий энергию из одного места пространства в другое носитель энергии можно математически рассматривать как вектор, а упорядоченное движение множества носителей энергии можно рассматривать как векторное поле.

Изложением на языке математики Закона Сохранения Энергии является формула Остроградского-Гаусса: поток вектора через замкнутую поверхность равен интегралу от дивергенции по объёму, ограниченному этой поверхностью. Любое нарушение равенства интегралов в формуле Остроградского-Гаусса является в физике свидетельством нарушения Закона Сохранения Энергии. Это было детально исследовано не только Карлом Гауссом, строго доказано как математический факт Михаилом Остроградским, но было использовано Дж. К. Максвелом при создании электродинамики. Повторять их объёмные выкладки здесь, в ущерб наглядности, нет смысла. Для устранения нарушений Закона Сохранения Энергии Дж. К. Максвел ввёл в электродинамику токи смещения (вихревые токи), что в дальнейшем привело к открытию электромагнитных волн, созданию радиосвязи и электроники.

Несколько важных замечаний. Все тела для упрощения будем считать имеющими пренебрежимо малые точечные размеры. Создаваемое телом гравитационное поле будем математически рассматривать как векторное поле, точечным источником которого является тело, а само поле направлено всегда от источника. Поток вектора через замкнутую поверхность при нахождении точечного источника векторного поля вне ограниченного замкнутой поверхностью объёма всегда будет равен нулю. Сумма потоков векторов двух и более векторных полей так же будет равна нулю, если все точечные источники векторных полей находятся вне данного объёма. Равенство интегралов в формуле Остроградского-Гаусса должно всегда выполняться в любой момент/интервал времени, иначе происходит нарушение Закона Сохранения Энергии.

Проведём следующий эксперимент. Выделим в пространстве некую выпуклую область с замкнутыми границами V и направим через неё точечное тело массы m со скоростью v. В момент времени t₀ фиксируется начальное состояние рассматриваемой системы, в моменты времени t₁ и t₂ тело пересекает границы замкнутой области V, в момент времени t₃ фиксируется конечное состояние системы. Энергия, заключённая в замкнутой области V согласно формулы Остроградского-Гаусса будет меняться только в моменты пересечения телом m границ области V. Поскольку энергия тела m не меняется, то равенство интегралов в формуле Остроградского-Гаусса сохраняется в любой момент/интервал времени.

Поместим теперь эту экспериментальную установку в гравитационное поле тела массы M на расстоянии R и повторим эксперимент. Для упрощения тело m изначально направим строго в сторону тела M. Тело m приобрело за счёт гравитационного притяжения к M дополнительную энергию при движении через объём V, а суммарная энергия объёма V, рассчитанная как поток вектора, после покидания телом m объёма V изменилась и стала отрицательной. Не будет выполняться равенство обеих частей формулы Остроградского-Гаусса и для любых моментов/интервалов времени когда тело m находится внутри объёма V, поскольку при отсутствии векторных полей поток вектора меняется только в моменты пересечения телом m границ V. Энергия не может быть отрицательной. Энергия не может появляться из ниоткуда и исчезать неизвестно куда. Возникло нарушение равенства интегралов, а значит проявилось нарушение Закона Сохранения Энергии.

Проведём ещё раз второй эксперимент, но уже если гравитационное поле является носителем части энергии создающего это поле тела. В этом случае появились дополнительные источники энергии M и m. По формуле Остроградского-Гаусса рассчитаем возникающие потоки энергии. Суммарный поток энергии, которую несут гравитационные поля, направлен от тела M, а тело m приобретает дополнительную энергию, равную работе внешних сил суммарного потока энергии, но приобретаемый телом импульс будет такой, чтобы не нарушался Закон Сохранения Энергии. Несложно убедиться, что в этом эксперименте в любой момент/интервал времени выполняется равенство в формуле Остроградского-Гаусса.

Формула Остроградского-Гаусса указывает единственный путь исполнения Закона Сохранения Энергии для гравитации: нарушения Закона Сохранения Энергии нет тогда и только тогда, когда гравитационное поле уносит часть энергии создающего это поле тела. Даже без теоремы Пуанкаре-Перельмана несложно убедиться, что искривление пространства-времени должно приводить к нарушению равенства в формуле Остроградского-Гаусса если гравитационное поле не уносит часть энергии образующего это поле тела. Действительно, с точки зрения физики метрика пространства — это всего лишь математическая абстракция, которая предназначена для согласования математической модели с наблюдаемой картиной мира. Математическая абстракция не является объектом материального мира, а значит не является носителем энергии, а значит не может изменять энергию объектов материального мира без нарушения Закона Сохранения Энергии. Следовательно, имеющее массу материальное тело создаёт гравитационное поле за счёт расходования своей энергии на создание собственного гравитационного поля, а гравитационное взаимодействие есть исключительно следствие расходования энергии имеющими массу объектами материального мира на создание ими собственных гравитационных полей.

Теорема об эквивалентности инертной и гравитационной масс доказана, поскольку нет самостоятельной гравитационной массы, а есть лишь взаимодействие инертных масс через создаваемые инертными массами гравитационные поля.

Если формула Пуанкаре-Эйнштейна E=m*c² верна, то фотон теряет свою массу/энергию на создаваемое им собственное гравитационное поле и с течением времени, с потерей массы/энергии, приобретает «красное смещение». Величина «красного смещения» как потери энергии определяется не только постоянной Хаббла, но и гравитационной постоянной как мощность излучаемой телом энергии на создание собственного гравитационного поля. Отсюда следует, что никакого Большого Взрыва не было. Помимо эффекта Доплера есть потеря фотоном своей энергии на создание собственного гравитационного поля. Каждый несущий энергию и обладающий массой объект материального мира теряет свою массу/энергию на создание собственного гравитационного поля постепенно «высыхая» и превращаясь в «пар» гравитационного поля. Следовательно, должны существовать условия конденсации гравитационного «пара» обратно в объекты материального мира. И действительно, астрономами в межгалактическом пространстве наблюдаются не только молодые звёзды, но и образующиеся молодые галактики, вроде Магеллановых Облаков, состоящих преимущественно из молодых звёзд. Кроме того, если «чёрные дыры» полностью поглощают все объекты материального мира, то как они осуществляют гравитационное взаимодействие с веществом, находящимся вне «горизонта событий»? Астрономическими наблюдениями зафиксировано, что поглощаемое «чёрной дырой» вещество приобретает энергию. Однако, носителями энергии, согласно современным воззрениям, НЕ являются гравитационное поле «чёрной дыры» и искривлённое «чёрной дырой» пространство. А значит вещество приобретает энергию неизвестно откуда. А значит налицо нарушение Закона Сохранения Энергии.

Предлагаемый подход к Единой Теории Материи устраняет нарушение Закона Сохранения Энергии действующими воззрениями на гравитацию как искривление пространства-времени и даёт уже физическое объяснение многим известным явлениям. Например, «реликтовому излучению», «красному смещению», искривлению траектории движения фотона, «тёмной материи», «чёрным дырам» и Второму Началу Термодинамики. Если физика — это предназначенная для описания некоторого класса явлений окружающего мира формальная система (шестая проблема Гилберта), то предлагаемая модель гравитации усиливает мощность физики как формальной системы настолько, что в соответствии с второй «Сильной» теоремой Курта Гёделя позволяет объяснять уже с точки зрения и в рамках самой физики некоторые явления окружающего мира, которые ранее принимались без физического объяснения, аксиоматически, как данность. Из теорем Гёделя следует решение и шестой проблемы Гилберта,: физика, как и любая другая формальная система, задаётся набором аксиом, а все высказывания (теоремы) в рамках физики как формальной системы строятся на основе формальной логики, благодаря чему помимо качественного описания явлений окружающего мира физикой появляется дополнительная возможность непротиворечивого количественного описания тех же явлений уже языком математики. Неформальные системы, например «вечный двигатель» или бред сумасшедшего, могут и не использовать аксиомы и/или формальную логику для своего построения.

В начале XX века нарушение Закона Сохранения Энергии «фиолетовой катастрофой» привело к созданию квантовой механики и ядерной физики, полётам в космос, микроэлектронике и т.д. Специальная Теория Относительности и квантовая механика отменили Ньютоново дальнодействие, но в силу недостаточности знаний в начале XX века вместо физического объяснения гравитации была предложена математическая абстракция искривления пространства-времени. Математика не заменяет физику, а лишь дополняет физику, усиливает. Теперь, когда дано физическое объяснение гравитации, без создания Единой Теории Материи дальше двигаться нельзя. И прежде всего следует определиться с аксиомами самой физики, из которых неоспоримыми являются Закон Сохранения Энергии и Закон Единообразия Материи. Нарушение Закона Сохранения Энергии «красной катастрофой» должно привести в XXI веке к созданию Единой Теории Материи.

Именно потому, что создавать/развивать Единую Теорию Материи предстоит прежде всего молодым, Автором была специально выбрана такая форма изложения, доступная для понимания даже школьникам старших классов и студентам младших курсов, которая без сложных и объёмных математических выкладок демонстрирует нарушение Закона Сохранения Энергии действующими воззрениями на гравитацию как искривление пространства-времени, предлагает физический путь преодоления нарушения Закона Сохранения Энергии и не навязывает Читателю своего видения Единой Теории Материи. Например, физическое объяснение принимаемых в настоящее время аксиоматически скорости света, Лоренц-фактора и постулатов Бора. Автор не Бог, может и ошибаться…

1974год -:- 09 января 2019 года

Аверьянов Юрий Иванович

---

Он обязан выполняться, поскольку одна из аксиом самой физики это как раз Закон Сохранения Энергии. Аксиомы математики лишь дополняют, усиливают физику (формальную систему для описания физического класса явлений окружающего материального мира) не отменяя аксиом самой физики. Описание явления не заменяет само явление. А абстракция искривления пространства-времени приводит как раз к нарушению Закона Сохранения Энергии. И я показал как это происходит. Т.е., искривление приводит к отмене минимум основной аксиомы физики (Закону Сохранения Энергии), а значит к отмене самой физики. Ну так СТО и ОТО — это всего лишь математические абстракции, к материальному миру не имеющие никакого отношения. Вернее, пытающиеся его описать без учёта аксиом физики.

Энергию материального объекта (носителя энергии) может изменять только другой материальный объект также являющийся носителем энергии. Энергия не может браться из ниоткуда и исчезать неизвестно куда. Пространство-время не является носителем энергии. Следовательно, только создаваемое материальным объектом гравитационное поле является носителем энергии, поскольку изменяет энергию других материальных объектов. То, что гравитационное поле занимает некое место в пространстве, не наделяет сами пространство и время энергией. Носители энергии (гравитоны), которые мы не можем наблюдать непосредственно известными нам сенсорами, занимают место в пространстве не наделяя пространство энергией.

Не случайно Пуанкаре выдвинул гипотезу о том, что доказанная для линейного однородного пространства формула Остроградского-Гаусса справедлива и для неоднородного нелинейного пространства. Формула Остроградского-Гаусса — это математическое изложение Закона Сохранения Энергии. Пуанкаре выдвинул свою гипотезу в ответ на то, что Эйнштейн применил математическую абстракцию искривления пространства-времени для согласования математической (абстрактной) модели мира с наблюдаемой картиной реального (материального) мира.

Пуанкаре не смог доказать несколькосм специальных случаев, поэтому его гипотеза была переформулирована для недоказанных специальных случаев, в результате чего «огрызки» гипотезы потеряли очень существенную семантическую часть. Мне повезло и я в 70-х годах читал оригинальную постановку гипотезы Пуанкаре. Недоказанные случаи и доказал Перельман. Во времена Пуанкаре (самое начало XX века) ещё не были доказаны теоремы Гёделя (1931-1934 годы) и не была разработана теория формальных языков (систем), поэтому я поражаюсь предвидению Пуанкаре.

Не случайно многие читали вторую часть ОТО Эйнштейна, но после его смерти в его архиве не нашлось ни одной строчки из второй части ОТО. Он её сжёг так же, как Гоголь сжёг вторую часть «Мёртвых душ». Как я понимаю, перед смертью Эйнштейн понял что хотел сказать ему Пуанкаре выдвинув свою гипотезу. А хотел он ему сказать, что Французская Академия Наук ещё в XVIII веке прекратила принимать заявки на «вечные двигатели»…

Category:

• Россия
• Cancel

Тяжёлая дорога домой

Вот так добирается домой сотрудник посолства СЩА в Москве Наварро Николас Сторми. Тяжёлая работа у сотрудников американского посольства.

Categories:

• Наука
• Технологии
• История
• Cancel

самоусложнение алгоритмов

1. Нейман показал, что возможно самовоспроизведение автоматов

Дж. фон Нейман, Теория самовоспроизводящихся автоматов. М.: «Мир», 1971.
ru.wikipedia.org/wiki/Автомат_фон_Неймана

2. я показал, что возможно самоусложнение алгоритмов

я хочу показать (и якобы понял как это возможно), что возможно построение сознания и сильного ИИ, и следовательно возможно самоусложнение алгоритмов/автоматов начиная с некоторого достаточного уровня сложности

3. отдельная задача — возможность доказать самоусложнение с нуля до «достаточного уровня сложности», тоже весьма интересная и достойная задача и очень сложная имхо

а вот доказать, что п.3 невозможен, я не уверен, что вообще можно

и как идея неопределенному кругу лиц
4. сделать типа клеточную автоматную среду по типу как у Неймана или как в игре Жизнь Конвея
есть среда и есть правила среды функционирования автоматов и надо както показать что это все может развиться до автоматов Неймана

но этого тоже будет недостаточно, с самовоспроизводящихся автоматов до самоусложняющихся автоматов дистанция еще больше похоже, чем с 0 до самовоспроизведения

итак есть три задачи
1. показать, что возможно самоусложнение с 0 до самовоспроизводящихся автоматов Неймана
2. показать, что возможно самоусложнение с самовоспроизводящихся автоматов до самоусложняющихся алгоритмов
3. показать, что возможно самоусложнение алгоритмов (якобы я эту задачу решил)

ps навеяно дискуссией с mns2012
Достойный взгляд на проблему
https://mns2012.livejournal.com/507771.html

Оригинал взят у sokura в Трусливые учёные
Оригинал взят у ss69100 в Трусливые учёные

Автор — Дмитриев Александр Леонидович, доктор технических наук, профессор Балтийского университета Военмех.

Соседство двух слов в заглавии этой заметки, на первый взгляд, кажется невозможным. Ученые – и вдруг трусливые! Быть такого не может!

Наука всегда смело шагает вперед, открывая дальние горизонты мысли, решая самые трудные проблемы и сметая препятствия на своем пути.

Но, как показано только на двух приведенных ниже примерах, жизнь науки и ее деятелей далеко не так проста.

Трусливые ученые, ученые шкурники, были, есть и наверняка останутся.

Пример первый: освоение околоземного пространства и космонавтика. Усомниться в том, что американцы побывали на Луне, в серьезных научных кругах считается проявлением наивности, невежества и просто дурным тоном.

Как ни добивайтесь, любознательные, ответов на вопросы, почему космонавты Аполлонов такими бодрячками шествовали по палубе авианосца доложить о благополучном прибытии с Луны, как им посчастливилось уцелеть в убийственных потоках космического излучения, где находятся сотни килограммов привезенных лунных камней и зачем эти камни так надежно спрятаны, внятного ответа никто из авторитетных ученых вам не даст.

Между тем, ответ на все приведенные вопросы прост¸ как сама правда: не было их там! Но трусят все: администраторы, ученые, даже мужественные космонавты – опасаются лишиться работы и жизни, исполняя обязательства врать и дальше об успешных полетах людей к Луне. Времена Джордано Бруно и Галилея миновали, а их порядочность и научная принципиальность современными интеллектуалами давно осмеяны.

Второй пример немного сложнее: теория относительности и гравитация.

Более сотни лет всеми средствами массовой информации восхваляется «величайшая теория относительности» Эйнштейна. Ее критика объявлена научным невежеством, а иногда и проявлением оголтелого антисемитизма.

Если находятся экспериментаторы, осмелившиеся представить в своих научных статьях результаты, противоречащие теории относительности, со стороны ортодоксов-релятивистов они подвергаются замалчиванию либо, наоборот, дружному шельмованию.

Эти исследователи, а заодно и журналы, в которых их статьи опубликованы, презрительно нарекаются самыми грубыми, вплоть до нецензурных, эпитетами. Провозглашена замечательная научная идеология: «физика без теории относительности — это физика обезьян!» (правда, среди этих «обезьян» следует упомянуть не знавших теории относительности Ньютона, Ломоносова, Фарадея, Максвелла, Менделеева и многих других).

К примеру, физик-экспериментатор получил результаты, доказывающие уменьшение силы гравитации при росте температуры взаимодействующих тел. Опубликовать эти результаты никакой «серьезный» научный журнал не посмеет, опасаясь потерять статус научного издания.

А все дело в том, что уменьшение силы гравитации при росте температуры тел явно противоречит теории Эйнштейна и, в частности, указывает на невозможность гравитационного сжатия (коллапса) до состояния «черной дыры» — любимой, очень хлебной (приносящей немалые доходы) темы современных теоретиков-астрофизиков.

Как и в первом примере, причиной отмеченной ученой трусости, в сущности, является страх коллег-ученых потерять работу, попросту — «кормушку».

Страх этот столь велик, что авторитетные ученые сторонятся поддержки экспериментальных исследований, в которых эффекты теории относительности (ведь чем черт не шутит!) могут не подтвердиться – так им, авторитетам, спокойнее.

Феномен трусливых ученых довольно типичен для современной науки. Его возникновение связано как с упадком общественной значимости, авторитета науки, так и с внедрением в научную среду разного рода шоуменов и «бизнесменов» (проще говоря, — прохвостов) от науки. Изгнать этих торгующих из храма науки под силу лишь гению.

А.Л. Дмитриев
Источник

=============================
[Сделать перепост всего текста ]Перепост всего текста

Скопируйте весь текст в рамке и введите его в поле HTML-редактора у себя в ЖЖ, войдя туда через кнопку «Новая запись». И не забудьте внести название в заголовок и нажать на кнопку «Отправить в …».

=============================

Структура общего решения системы уравнений

Однородная система линейных уравнений

всегда совместна, так как имеет тривиальное решение . Если ранг матрицы системы равен количеству неизвестных , то тривиальное решение единственное. Предположим, что . Тогда однородная система имеет бесконечно много решений. Заметим, что расширенная матрица однородной системы при элементарных преобразованиях строк приводится к упрощенному виду , т.е. . Поэтому из (5.11) получаем общее решение однородной системы уравнений :

Получим другую форму записи решений однородной системы, которая раскрывает структуру множества решений. Для этого подчеркнем следующие свойства.

Свойства решений однородной системы уравнений

1. Если столбцы — решения однородной системы уравнений, то любая их линейная комбинация также является решением однородной системы.

В самом деле, из равенств следует, что

т.е. линейная комбинация решений является решением однородной системы.

2. Если ранг матрицы однородной системы равен , то система имеет линейно независимых решений.

Действительно, по формулам (5.13) общего решения однородной системы найдем частных решений , придавая свободным переменным следующие стандартные наборы значений (всякий раз полагая, что одна из свободных переменных равна единице, а остальные — равны нулю):

которые линейно независимы. В самом деле, если из этих столбцов составить матрицу, то последние ее строк образуют единичную матрицу. Следовательно, минор, расположенный в последних строках не равен нулю (он равен единице), т.е. является базисным. Поэтому ранг матрицы будет равен . Значит, все столбцы этой матрицы линейно независимы (см. теорему 3.4).

Любая совокупность линейно независимых решений однородной системы называется фундаментальной системой (совокупностью) решений .

Заметим, что фундаментальная система решений определяется неоднозначно. Однородная система может иметь разные фундаментальные системы решений, состоящие из одного и того же количества линейно независимых решений.

Теорема 5.3 об общем решении однородной системы. Если — фундаментальная система решений однородной системы уравнений (5.4), то столбец

при любых значениях произвольных постоянных также является решением системы (5.4), и, наоборот, для каждого решения х этой системы найдутся такие значения произвольных постоянных , при которых это решение удовлетворяет равенству (5.14).

Прямое утверждение теоремы следует из свойства 1 решений однородной системы. Докажем обратное утверждение о том, что любое решение можно представить в виде (5.14). Для этого составим матрицу , приписав к столбцам фундаментальной системы решений столбец

Найдем ранг этой матрицы. Так как первые столбцов линейно независимы, то . Так как каждый из столбцов матрицы является решением системы , то по первой формуле из (5.13) получаем

Следовательно, первая строка матрицы является линейной комбинацией последних строк этой матрицы.

По второй формуле из (5.13) получим, что вторая строка матрицы является линейной комбинацией последних строк этой матрицы, и т.д. По r-й формуле из (5.13) получим, что r-я строка матрицы является линейной комбинацией последних строк этой матрицы. Значит, первые строк матрицы можно вычеркнуть и при этом ранг матрицы не изменится. Следовательно, , так как после вычеркивания в матрице будет всего строк. Таким образом, . Значит, есть базисный минор матрицы , который расположен в первых ее столбцах, а столбец не входит в этот базисный минор. Тогда по теореме о базисном миноре найдутся такие числа , что

Итак, обратное утверждение доказано.

Алгоритм решения однородной системы уравнений

1-5. Выполнить первые 5 пунктов алгоритма Гаусса. При этом не требуется выяснять совместность системы, так как любая однородная система имеет решение (пункт 3 метода Гаусса следует пропустить). Получить формулы (5.11) общего решения, которые для однородной системы будут иметь вид (5.13).

Если ранг матрицы системы равен числу неизвестных , то система имеет единственное тривиальное решение и процесс решения заканчивается.

Если ранг матрицы системы меньше числа неизвестных , то система имеет бесконечно много решений. Структуру множества решений находим в следующих пунктах алгоритма.

6. Найти фундаментальную систему решений однородной системы. Для этого подставить в (5.13) последовательно стандартных наборов значений свободных переменных, в которых все свободные переменные равны нулю, кроме одной, равной единице (см. свойство 2 решений однородной системы).

7. Записать общее решение однородной системы по формуле (5.14).

1. В пункте 6 алгоритма вместо стандартного набора значений свободных переменных можно использовать и другие наборы значений, лишь бы они обеспечивали линейную независимость получаемых частных решений однородной системы.

2. Матрица столбцы которой образуют фундаментальную систему решений однородной системы, называется фундаментальной. Используя фундаментальную матрицу, общее решение (5.14) однородной системы можно записать в виде

3. Если базисный минор матрицы расположен в левом верхнем углу (в первых строках и первых столбцах), то упрощенный вид расширенной матрицы (5.9) однородной системы можно представить в виде блочной матрицы

Тогда блочная матрица размеров является фундаментальной. В этом можно убедиться, используя стандартные наборы значений свободных переменных. Применение блочных матриц может служить вторым способом нахождения фундаментальной системы решений.

Пример 5.4. Найти фундаментальную систему решений и общее решение однородной системы

Решение. 1. Составляем расширенную матрицу системы

2-4. Используя элементарные преобразования над строками матрицы , приводим ее к ступенчатому, а затем и к упрощенному виду (см. решение примера 5.3):

Пункт 3 метода Гаусса пропускаем.

5. Переменные — базисные, а — свободные. Записываем формулу (5.13) общего решения однородной системы

6. Находим фундаментальную систему решений. Так как и , надо подобрать линейно независимых решения. Подставляем в систему стандартные наборы значений свободных переменных:

В результате получили фундаментальную систему решений

7. Записываем общее решение однородной системы по формуле (5.14):

Заметим, что фундаментальную систему решений можно получить, взяв иные наборы значений свободных переменных. Например, и . Тогда получим другую фундаментальную систему решений

Несмотря на различия, обе формулы задают одно и то же множество решений.

Структура общего решения неоднородной системы уравнений

Ранее была выведена формула (5.11) общего решения системы линейных уравнений. Получим другую форму записи, отражающую структуру множества решений.

Рассмотрим неоднородную систему и соответствующую ей однородную систему . Между решениями этих систем имеются связи, выражающиеся следующими свойствами.

Свойства решений неоднородной системы уравнений

1. Разность двух решений и неоднородной системы есть решение однородной системы.

Действительно, из равенств и следует, что .

2. Пусть — решение неоднородной системы. Тогда любое решение неоднородной системы можно представить в виде

В самом деле, для любого решения неоднородной системы разность по свойству 1 является решением однородной системы, т.е. — решение однородной системы.

Теорема 5.4 о структуре общего решения неоднородной системы.

Пусть — решение неоднородной системы, а — фундаментальная система решений соответствующей однородной системы уравнений. Тогда столбец

при любых значениях [i]произвольных постоянных является решением неоднородной системы, и, наоборот, для каждого решения этой системы найдутся такие значения произвольных постоянных , при которых это решение удовлетворяет равенству (5.15).[/i]

Говорят, что общее решение неоднородной системы есть сумма частного решения неоднородной системы и общего решения соответствующей однородной системы.

Доказательство теоремы вытекает из свойств 1, 2 и теоремы 5.3.

Алгоритм решения неоднородной системы уравнений

1-5. Выполнить первые 5 пунктов метода Гаусса решения системы уравнений и получить формулу общего решения неоднородной системы вида (5.11).

6. Найти частное решение неоднородной системы, положив в (5.11) все свободные переменные равными нулю.

7. Записав формулы (5.13) общего решения соответствующей однородной системы, составить фундаментальную систему ее решений. Для этого подставить в (5.13) последовательно стандартных наборов значений свободных переменных, в которых все переменные равны нулю, за исключением одной, равной единице.

8. Записать общее решение неоднородной системы по формуле (5.15).

1. Используя фундаментальную матрицу однородной системы , решение неоднородной системы можно представить в виде

2. Если базисный минор матрицы расположен в левом верхнем углу (в первых строках и первых столбцах), то упрощенный вид расширенной матрицы (5.9) неоднородной системы можно представить в виде блочной матрицы

Тогда блочная матрица оказывается фундаментальной (см. п.3 замечаний 5.3), а столбец является частным решением неоднородной системы (в этом можно убедиться, подставляя в (5.11) нулевой набор свободных переменных). Используя блочные матрицы, общее решение (5 15) неоднородной системы можно представить в виде

где — столбец произвольных постоянных. Полученную формулу можно считать вторым способом решения неоднородной системы.

Пример 5.5. Найти структуру (5.15) общего решения неоднородной системы

Решение. 1-5. Первые 5 пунктов метода Гаусса выполнены при решении примера 5.3, где получены формулы общего решения неоднородной системы:

Переменные — базисные, а — свободные.

6. Полагая , получаем частное решение неоднородной системы .

7. Находим фундаментальную систему решений однородной системы (см. пример 5.4):

8. Записываем по формуле (5.15) общее решение неоднородной системы

Искомая структура множества решений найдена.

Получим формулу общего решения вторым способом , используя п.2 замечаний 5.4. При решении примера 5.3 расширенная матрица системы была приведена к упрощенному виду. Разбиваем ее на блоки:

Записываем частное решение неоднородной системы

и составляем фундаментальную матрицу:

По формуле (5.16) получаем общее решение неоднородной системы, которое преобразуем к виду (5.15):

Эквивалентность СЛАУ при элементарных преобразованиях

Определения

Система m линейных уравнений с n неизвестными(или, линейная система) в линейной алгебре — это система уравнений вида

a11x1 + a12x2 + … + a1nxn = b1,	(1)
a21x1 + a22x2 + … + a2nxn = b2,
. . . . . . . . . . . . . . . . . .
am1x1 + am2x2 + … + amnxn = bm.

Система (1) называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = bm = 0), иначе — неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Решение системы (1) — совокупность n чисел c₁, c₂, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все ее уравнения в тождества.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения c₁ (1) , c₂ (1) , …, cn (1) и c₁ (2) , c₂ (2) , …, cn (2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:

c₁ (1) = c₁ (2) , c₂ (1) = c₂ (2) , …, cn (1) = cn (2) .

Совместная система вида (1) называется определенной, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределенной. Если уравнений больше, чем неизвестных, она называется переопределённой.

Матричная форма Править

Система линейных уравнений может быть представлена в матричной форме как:

или, согласно правилу перемножения матриц,

Методы решения системы (1) Править

Прямые методы Править

§ Метод прогонки – Для трехдиагональных матриц

Приближенные методы Править

§ Метод Якоби (метод итераций)

Метод Крамера (Крамера правило) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причем для таких уравнений решение существует и единственно).

Описание метода

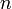
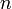
Для системы линейных уравнений с неизвестными (над произвольным полем) (число уравнений совпадает с числом переменных).

с определителем матрицы системы , отличным от нуля, решение записывается в виде:

,

.

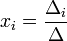
(i-й столбец матрицы системы заменяется столбцом свободных членов).

Рангом матрицы A называется наибольший из порядков миноров матрицы A , отличных от нуля. Ранг нулевой матрицы считается равным нулю.

Алгоритм вычисления ранга матрицы:

• матрица приводится к ступенчатому с помощью элементарных преобразований;
• количество ненулевых строк в полученной матрице будет равно рангу первоначальной матрицы.

Свойства ранга матрицы:

• ранг матрицы не превосходит меньшего из ее размеров;
• ранг матрицы равен нулю тогда и только тогда, когда матрица нулевая;
• ранг матрицы не изменится, если из нее вычеркнуть все нулевые строки и столбцы;
• ранг матрицы не изменится при ее транспонировании;
• элементарные преобразования матрицы не меняют ее ранга

Элементарные преобразования матрицы.

Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.

Определение

Элементарными преобразованиями строк называют:

§ перестановка местами любых двух строк матрицы;

§ умножение любой строки матрицы на константу , ;

§ прибавление к любой строке матрицы другой строки, умноженной на константу , .

Аналогично определяются элементарные преобразования столбцов.

Элементарные преобразования обратимы.

Обозначение указывает на то, что матрица может быть получена из путём элементарных преобразований (или наоборот).

Свойства

Инвариантность ранга при элементарных преобразованиях

Эквивалентность СЛАУ при элементарных преобразованиях

Назовём элементарными преобразованиями над системой линейных алгебраических уравнений:

§ умножение уравнения на ненулевую константу;

§ сложение одного уравнения с другим, умноженным на некоторую константу.

Т.е. элементарные преобразования над её расширенной матрицей. Тогда справедливо следующее утверждение:

Теорема (об эквивалентности систем уравнений при элементарных преобразованиях). Система линейных алгебраических уравнений, полученная путём элементарных преобразований над исходной системой, эквивалентна ей.

Напомним, что две системы называются эквивалентными, если множества их решений совпадают.

Теорема 1. ( Об эквивалентности пар на плоскости ). Две пары,
лежащие в одной плоскости и имеющие равные по величине и по знаку моменты,
эквивалентны.

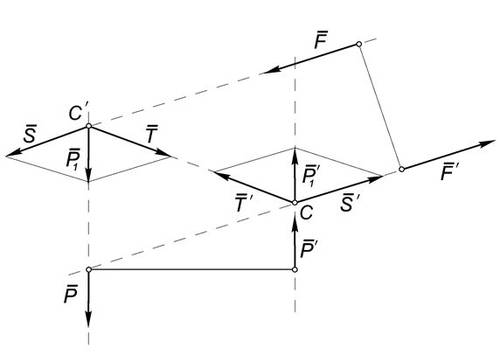
Для доказательства рассмотрим две пары $(vec{P}, vec{P’})text{ и }(vec{F}, vec{F’})$, лежащие в одной плоскости и имеющие равные по величине и по знаку моменты (Рис.1).

Продолжим линии действия сил пар до их пересечения в точках С и С’.

На основании следствия из аксиомы 3 действие сил $vec{P}text{ и }vec{P’}$ не изменится, если эти силы перенести в эти точки, то есть $(vec{P}, vec{P’}) sim (vec{P_1}, vec{P_1′})$.

Воспользовавшись аксиомой 4, заменим силу $vec{P_1}$ составляющими $vec{S}text{ и }vec{T}$,
направленными, соответственно, вдоль линии действия силы $vec{F}$, и по прямой
СС’. Аналогично поступим с силой $vec{Р1′}$, заменив ее составляющими $vec{S’}text{ и }vec{T’}$.

По построению $vec{T} = — vec{T’}$, поэтому согласно аксиоме 2: $(vec{T}, vec{T’}) sim 0$ и в соответствии с аксиомой 3 эту систему можно исключить.

Таким образом,

$$(vec{P}, vec{P’}) sim (vec{P_1}, vec{P_1′}) sim ((vec{S}, vec{T}),(vec{S’}, vec{T’})) sim ((vec{S}, vec{S’}),(vec{T}, vec{T’})) sim (vec{S}, vec{S’})$$,

, то есть пары сил $(vec{P}, vec{P’})text{ и }(vec{S}, vec{S’})$ эквивалентны.

Остается доказать эквивалентность пар $(vec{S}, vec{S’})text{ и }(vec{F}, vec{F’}). Поскольку эти пары имеют равные плечи, они будут эквивалентны, если будут равны их моменты.

По условию теоремы моменты пар $(vec{P}, vec{P’})text{ и }(vec{F}, vec{F’})$ равны. Таким образом:

$$M(vec{F}, vec{F’}) = M(vec{P}, vec{P’}) = M(vec{P_1}, vec{P_1′}) = M_C(vec{P_1})$$

В силу теоремы Вариньона:

$$M_C(vec{P_1}) = M_C(vec{S}) + M_C(vec{T}) = M_C(vec{S})$$

, поскольку линия действия силы $vec{T}$ проходит через точку С и ее момент равен нулю. Итак:

$$M(vec{F}, vec{F’}) = M_C(vec{S}) = M(vec{S}, vec{S’})$$

, а значит пары $(vec{S}, vec{S’})text{ и }(vec{F}, vec{F’})$ будут эквивалентны.

Таким образом: $(vec{P}, vec{P’}) sim (vec{S}, vec{S’}) sim (vec{F}, vec{F’}), и теорема доказана.

Рассмотрим следствия этой теоремы, которые также можно рассматривать как свойства пар сил в дополнение к свойствам, рассмотренным в «Пара сил и ее свойства».

Следствия:

1. Действие пары сил на ТТ не меняется при ее перемещении в своей плоскости.

2. Действие пары сил на ТТ не изменится, если одновременно изменить плечо и силы пары, сохранив неизменным ее момент.

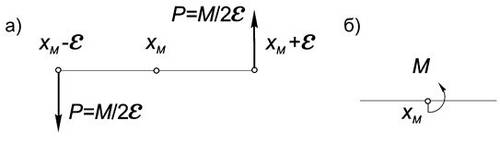
Рассмотрим в частности пару, представленную силами $pm P=frac{M}{2varepsilon}$ ,
приложенными к балке в точках $x=x_Mpmvarepsilon$ (Рис.2а). Плечо такой пары, равно
$2varepsilon$ , а ее момент равен M. При изменении ( будут меняться плечо и силы пары,
но величина ее момента останется равной первоначальному значению.

Определение 1. Моментом называется система, полученная из пары сил $pm P=frac{M}{2varepsilon}$ , при $varepsilonto 0$.

Таким образом, термин «момент» имеет в ТМ два значения:

1. момент как произведение силы на ее плечо и

2. момент как система, полученная из пары сил в соответствии с определением 1.

Отметим, что при таком предельном переходе плечо пары стремится к
нулю, а силы пары – к бесконечности. Полученный в соответствии с
определением 1 момент фактически является таким же самостоятельным
объектом в механике, как и сила, и в дальнейшем мы будем обозначать его
так, как показано на рис.2б.

Если для абсолютно твердого тела последний момент эквивалентен паре
сил, показанной на рис.2а , то в механике деформируемого тела действие
такого сосредоточенного момента, приложенного в точке х=хМ , существенно
отличается от действия пары сил.

Теорема 2. ( Об эквивалентности пар в пространстве ). Две пары,
лежащие в параллельных плоскостях и имеющие равные по величине и по знаку
моменты, эквивалентны.

Для доказательства этой теоремы нам понадобится следующая:

Лемма. Равнодействующая двух параллельных и равных по модулю сил
равна их сумме, а ее линия действия проходит посредине между точками их
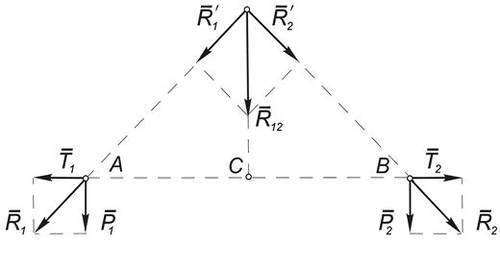
приложения (Рис.3).

Для доказательства леммы достаточно к системе двух сил $(vec{P_1}, vec{P_2})$ ,
приложенных соответственно в точках A и B, о которых идет речь в теореме,
добавить уравновешенную систему сил $(vec{T_1},vec{T_2})$ , а затем воспользоваться
аксиомой параллелограмма:

$$(vec{P_1}, vec{P_2}) sim ((vec{P_1}, vec{P_2}), (vec{T_1}, vec{T_2})) sim ((vec{P_1}, vec{T_1}), (vec{P_2}, vec{T_2})) sim (vec{R_1}, vec{R_2}) sim (vec{R_{12}})$$

, где $vec{P_1} = vec{P_2} = vec{P},,, vec{R_{12}} = 2cdot P$ , а AС = BC .

Переходя к доказательству теоремы, рассмотрим две пары сил $(vec{P_1}, vec{P_2})text{ и }(vec{F_1}, vec{F_2})$, имеющие равные моменты и лежащие в параллельных плоскостях П₁ и П₂ соответственно (Рис.4).

Построим в плоскости П₂ отрезок CD, равный и параллельный отрезку
АВ и приложим в точках C и D две системы уравновешенных сил: $(vec{S_1}, vec{S_2}) sim 0text{ и }(vec{T_1}, vec{T_2}) sim 0$
, выбрав силы $vec{S}$ и $vec{T}$ равными по модулю и параллельными силам $vec{P}$.

На основании аксиом 2, 3 и последней леммы:

$$ (vec{P_1}, vec{P_2}) sim ((vec{P_1}, vec{P_2}), (vec{S_1}, vec{S_2}), (vec{T_1}, vec{T_2})) sim ((vec{P_1}, vec{T_1}), (vec{P_2}, vec{S_2}), (vec{S_1}, vec{T_2})) sim
\ sim ((vec{R_1}, vec{R_2}), (vec{S_1}, vec{T_2})) sim (vec{S_1}, T_2)
$$

, поскольку $vec{R_1} sim (vec{P_1}, vec{T_1})$ и $vec{R_2} sim (vec{P_2}, vec{S_2})$ также образуют уравновешенную систему сил, которую можно исключить.

Таким образом, мы получили две пары сил: $(vec{S_1}, vec{T_2})$ и $(vec{F_1}, vec{F_2})$ , которые
лежат в одной плоскости и имеют равные по величине и по знаку моменты. В
силу предыдущей теоремы 1 они будут эквивалентны, откуда следует, что

$$(vec{P_1}, vec{P_2}) sim (vec{S_1}, vec{T_2}) sim (vec{F_1}, F_2)$$

Теорема доказана.

Следствие. Действие пары сил на ТТ не изменится при ее перемещении в
параллельную плоскость, расположенную в пределах этого тела.