Теорема о циркуляции вектора напряженности
Теорема о циркуляции вектора напряженности
Теорема о циркуляции вектора напряженности электрического поля
Взаимодействие неподвижных зарядов реализуется посредством электростатического поля. Описывают электростатическое поле при помощи вектора напряженности ($overline{E}$), который определен как сила ($overline{F}$), действующая на единичный положительный заряд, размещенный в рассматриваемой точке поля:
[overline{E}=frac{overline{F}}{q}left(1right).]
Электростатические силы являются консервативными, это значит, что их работа по замкнутой траектории ($L$) равна нулю:
[A=ointnolimits_L{overline{F}doverline{r}=}qointnolimits_L{overline{E}doverline{r}=}0 left(2right),]
где $overline{r}$ — перемещение.
Интеграл в формуле (2) называется циркуляцией вектора напряженности электростатического поля. Циркуляция вектора $overline{E}$- это работа, которую могут совершить силы Кулона, перемещая положительный заряд равный единице по контуру.
Учитывая, что $qne 0$, получим:
[ointnolimits_L{overline{E}doverline{r}=}0 left(3right).]
Теорема о циркуляции вектора напряжённости электростатического поля говорит о том, циркуляция $overline{E}$ по замкнутому контуру равна нулю.
В дифференциальной форме теорему о циркуляции записывают как:
[rot overline{E}=0 left(4right).]
Такой вид записи как (4) удобно использовать для проверки потенциальности векторного поля. Потенциальное поле является безвихревым.
Как следствие из теоремы о циркуляции $overline{E}$: работа при перемещении заряда из одной точки поля в другую не зависит от формы траектории движения.
Из теоремы о циркуляции следует, что линии электростатического поля не бывают замкнутыми, они начинаются на положительных, а заканчиваются на отрицательных зарядах.
Теорема о циркуляции вектора напряженности магнитного поля
Физическая величина ($overline{H}$), являющаяся характеристикой магнитного поля, равная:
[overline{H}=frac{overline{B}}{{mu }_0}-{overline{P}}_m(5)]
называется напряженностью магнитного поля. $overline{B}$ — вектор магнитной индукции поля; ${mu }_0$ — магнитная постоянная; ${overline{P}}_m$- вектор намагниченности.
Циркуляция вектора напряженности магнитного поля равна алгебраической сумме токов проводимости, которые охвачены замкнутым контуром, по которому рассматривается циркуляция:
[ointlimits_L{overline{H}doverline{r}=sum{I_m}left(6right).}]
Если направление обхода контура связывается с направлением тока правилом правого винта, то ток в сумме (5) стоит со знаком плюс.
Циркуляция вектора напряженности в общем случае отлична от нуля, это означает, что магнитное поле — это вихревое поле, оно не является потенциальным.
Теорему о циркуляции вектора напряженности магнитного поля доказывают, опираясь на закон Био-Савара-Лапласа и принцип суперпозиции.
Теорема о циркуляции вектора $overline{H}$ исполняет роль, похожую на роль теоремы Гаусса для вектора напряженности электрического поля. Если имеется симметрия при распределении токов, то используя теорему о циркуляции $overline{H},$ находят саму напряженность магнитного поля.
Примеры задач с решением
Пример 1
Задание. Определите, является ли потенциальным электрическое поле, которое задано уравнением: $overline{E}left(x,yright)=Aleft(2xy overline{i}+left(x^2-y^2right)overline{j}right).$
Решение. Из теоремы о циркуляции, которая записана в дифференциальном виде:
[rot overline{E}=0 left(1.1right).]
следует, что если вихрь поля равен нулю, то поле потенциально. Используя определение ротора:
[rot overline{E}=left| begin{array}{ccc}
overline{i} & overline{j} & overline{k} \
frac{partial}{partial x} & frac{partial }{partial y} & frac{partial}{partial z} \
E_x & E_y & E_z end{array}
right|(1.2)]
найдем:
[rot overline{E}=rot left[Aleft(2xy overline{i}+left(x^2-y^2right)overline{j}right)right]=frac{partial E_y}{partial x}overline{k}-frac{partial E_x}{partial y}overline{k}left(1.3right).]
Частные производные от $overline{E}$ равны:
[frac{partial E_y}{partial x}=Acdot 2x;; frac{partial E_x}{partial y}=Acdot 2x left(1.4right).]
Подставляя (1.4) в (1.3), получаем, что
[rot overline{E}=rot left[Aleft(2xy overline{i}+left(x^2-y^2right)overline{j}right)right]=0.]
Ответ. Поле является потенциальным.
Пример 2
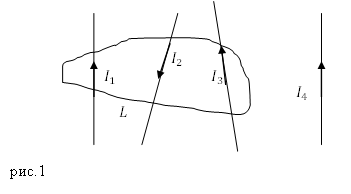
Задание. Какова циркуляция вектора напряженности магнитного поля для замкнутого контура $L$ (рис.1), если $I_1=5 A;; I_2=2 A;; I_3=10 A;; I_4=1 A?$
Решение. Основой для решения задачи служит теорема о циркуляции вектора напряжённости магнитного поля:
[ointlimits_L{overline{H}doverline{r}=sum{I_m}left(2.1right).}]
Контур $L$ охватывает три тока, следовательно:
[ointlimits_L{overline{H}doverline{r}=I_1-I_2+I_3.}]
Вычислим циркуляцию:
[ointlimits_L{overline{H}doverline{r}=5-2+10=13 (А).}]
Ответ. $ointlimits_L{overline{H}doverline{r}=13А .}$
Читать дальше: типы ядерных реакций.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Когда
зарядов много, при расчётах полей
возникают некоторые трудности.

их помогает теорема Гаусса. Суть теоремы
Гаусса
сводится к следующему: если произвольное
количество зарядов мысленно окружить
замкнутой поверхностью S,
то поток напряжённости электрического
поля через элементарную площадку dS
можно записать как dФ
= Есоsα۰dS
где α
— угол между нормалью к плоскости и
вектором напряжённости .
(рис.12.7)
Полный
же поток через всю поверхность будет
равен сумме потоков от всех зарядов,
произвольным образом распределённых
внутри её и пропорционально величине
этого заряда
(12.9)

поток вектора напряжённости сквозь
сферическую поверхность радиуса r,
в центре которой расположен точечный
заряд +q
(рис.12.8). Линии напряжённости перпендикулярны
поверхности сферы, α =0, следовательно
соsα
= 1. Тогда
или
Если
поле образовано системой зарядов, то
Теорема
Гаусса:
поток вектора напряжённости
электростатического поля в вакууме
сквозь любую замкнутую поверхность
равен алгебраической сумме зарядов,
заключенных внутри этой поверхности,
делённой на электрическую постоянную.
(12.10)
Если
внутри сферы зарядов нет, то Ф = 0.
Теорема
Гаусса позволяет сравнительно просто
рассчитать электрические поля при
симметрично распределённых зарядов.
Введём
понятие о плотности распределенных
зарядов.
-
Линейная
плотность обозначается τ и характеризует
заряд q,
приходящийся на единицу длины ℓ. В
общем виде может быть рассчитана по
формуле
(12.11)
При
равномерном распределении зарядов
линейная плотность равна
-
Поверхностная
плотность обозначается σ и характеризует
заряд q,
приходящийся на единицу площади S.
В общем виде определяется по формуле
(12.12)
При
равномерном распределении зарядов по
поверхности поверхностная плотность
равна
-
Объёмная
плотность обозначается ρ, характеризует
заряд q,
приходящийся на единицу объёма V.
В общем виде определяется по формуле
(12.13)
При
равномерном распределении зарядов она
равна .
-
Н
апряжённость
электростатического поля равномерно
заряженной сферы
(рис.12.9),
имеющей радиус r0.
Найдём модуль вектора
в какой-либо точке А, находящейся на
расстоянии r1
от центра
этой сферы.
Так
как заряд q
располагается на сфере равномерно, то
σ
= const.
Применим теорему Гаусса. Проведём сферу
радиусом через точку А. Поток вектора
напряжённости рис.12.9 сквозь
сферическую поверхность радиуса равен
соsα
= 1, так как α
= 0. По теореме Гаусса, .
или
(12.14)
Из
выражения (12.14) следует, что напряжённость
поля вне заряженной сферы такая же, как
напряжённость поля точечного заряда,
помещённого в центре сферы. На поверхности
сферы, т.е. r1
= r0
, напряжённость .
Внутри
сферы r1
< r0
(рис.12.9) напряжённость Е = 0, так как сфера
радиусом r2
внутри
никаких зарядов не содержит и, по теореме
Гаусса, поток вектора сквозь такую
сферу равен нулю.
-
Н
апряжённость
поля, создаваемого равномерно заряженным
бесконечно длинным цилиндром
Цилиндр
радиусом r0
равномерно
заряжен с поверхностной плотностью σ
(рис.12.10). Определим напряжённость поля
в произвольно выбранной точке А. Проведём
через точку А воображаемую цилиндрическую
поверхность радиусом R
и длиной ℓ. Вследствие симметрии поток
будет выходить только через боковые
поверхности цилиндра, так как заряды
на цилиндре радиуса r0
распределены по его поверхности
равномерно, т.е. линии напряжённости
будут радиальными прямыми, перпендикулярными
боковым поверхностям обоих цилиндров.
Так как поток через основание цилиндров
равен нулю (cos
α
= 0), а боковая поверхность цилиндра
перпендикулярна силовым линиям (cos
α
= 1), то
или
(12.15)
Выразим
величину Е через σ — поверхностную
плотность. По определению,
следовательно,
Подставим
значение q
в формулу (12.15)
(12.16)
По
определению линейной плотности,
, откуда ;
подставляем это выражение в формулу
(12.16):
(12.17)
т.е.
напряжённость поля, создаваемого
бесконечно длинным заряженным цилиндром,
пропорциональна линейной плотности
заряда и обратно пропорциональна
расстоянию.
-
Напряжённость
поля, создаваемого бесконечной
равномерно заряженной плоскостью
напряжённость поля, создаваемого
бесконечной равномерно заряженной
плоскостью в точке А. Пусть поверхностная
плотность заряда плоскости равна σ. В
качестве замкнутой поверхности удобно
выбрать цилиндр, ось которого
перпендикулярна плоскости, а правое
основание содержит точку А. Плоскость
делит цилиндр пополам. Очевидно, что
силовые линии перпендикулярны плоскости
и параллельны боковой поверхности
цилиндра, поэтому весь поток проходит
только через основания цилиндра. На
обоих основаниях напряжённость поля
одинакова, т.к. точки А и В симметричны
относительно плоскости. Тогда поток,
через основания цилиндра равен
Согласно
теореме Гаусса,
Так
как ,
то ,
откуда
(12.18)
Таким
образом, напряжённость поля бесконечной
заряженной плоскости пропорциональна
поверхностной плотности заряда и не
зависит от расстояния до плоскости.
Следовательно, поле плоскости является
однородным.
-
Напряжённость
поля, создаваемого двумя разноименно
равномерно заряженными параллельными
плоскостями

поле, создаваемое двумя плоскостями,
определяется по принципу суперпозиции
полей:
(рис.12.12). Поле, создаваемое каждой
плоскостью, является однородным,
напряжённости этих полей равны по
модулю, но противоположны по направлению:
.
По принципу суперпозиции напряжённость
суммарного поля вне плоскости равна
нулю:
Между плоскостями
напряжённости полей имеют одинаковые
направления, поэтому результирующая
напряжённость равна
(12.19)
Таким
образом, поле между двумя разноименно
равномерно заряженными плоскостями
однородно и его напряжённость в два
раза больше, чем напряжённость поля,
создаваемого одной плоскостью. Слева
и справа от плоскостей поле отсутствует.
Такой же вид имеет и поле конечных
плоскостей, искажение появляется только
вблизи их границ. С помощью полученной
формулы можно рассчитать поле между
обкладками плоского конденсатора.
Соседние файлы в папке Физика
- #
- #
- #
- #
- #
- #
- #
- #
Уравнения Максвелла — это 4 уравнения, которые описывают, как электрические и магнитные поля распространяются и взаимодействуют; т.е. эти уравнения (правила или даже законы) описывают процессы/взаимодействия электромагнетизма.
Эти правила описывают, как проходит управление поведением электрических и магнитных полей. Уравнения Максвелла показывают, что электрический заряд (положительный и отрицательный):
- Порождает электрическое поле (также если заряд изменяется со временем, то он вызывает появление электрического поля).
- В дальнейшем он вызывает появление магнитного поля.
Уравнения Максвелла в дифференциальной форме
Уравнение 1: Закон Гаусса или Теорема Гаусса

Дивергенция электрического поля равняется плотности заряда. Существует вязь между электрическим полем и электрическим зарядом.
Дивергенция в физике показывает, насколько данная точка пространства является источником или потребителем потока поля.
Очень кратко: Электрические поля расходятся от электрических зарядов: электрический заряд создаёт поле вокруг себя и, таким образом, действует как источник электрических полей. Это можно сравнить с краном, который является источником воды.
Ещё закон Гаусса говорит о том, что отрицательные заряды действуют как сток для электрических полей (способ, как вода стекает через отверстие стока). Это означает, что линии электрического поля имеют начало и поглощаются при электрическом заряде.
Заряды с одинаковым знаком отталкиваются друг от друга, а противоположные заряды притягиваются друг к другу (если есть два положительных заряда, они будут отталкиваться; а если есть один отрицательный и один положительный, они будут притягиваться друг к другу).
Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)

Можно создать электрическое поле, изменив магнитное поле.
Очень кратко: Закон Фарадея гласит, что изменяющееся магнитное поле внутри контура вызывает индуцированный ток, который возникает из-за силы или напряжения внутри контура. Это значит:
- Электрический ток порождает магнитные поля, а эти магнитные поля (вокруг цепи) вызывают электрический ток.
- Изменяющееся во времени магнитное поле вызывает распространение электрического поля.
- Циркулирующее во времени электрическое поле вызывает изменение магнитного поля во времени.
Уравнение 3: Закон Гаусса для магнетизма

Дивергенция магнитного потока любой замкнутой поверхности равна нулю. Магнитного монополя не существует.
Закон Гаусса для магнетизма утверждает (очень кратко):
- Магнитных монополей не существует.
- Расхождение полей B или H всегда равно нулю в любом объёме.
- На расстоянии от магнитных диполей (это круговой ток) магнитные поля текут по замкнутому контуру.
Уравнение 4: Закон Ампера

Магнитное поле создаётся с помощью тока или изменяющегося электрического поля.
Очень кратко: Электрический ток порождает магнитное поле вокруг тока. Изменяющийся во времени электрический поток порождает магнитное поле.
Уравнения Максвелла в интегральной и дифференциальной форме
Вспомним сначала в дифференциальной форме и следом будет в интегральной форме.
Уравнение 1: Закон Гаусса (Теорема Гаусса)

Это же уравнение в интегральной форме:

Поток вектора электрической индукции D через любую замкнутую поверхность равняется сумме свободных зарядов, охваченных этой поверхностью. Электрическое поле создаётся нескомпенсированными электрическими зарядами (это те, что создают вокруг себя своё собственное электрическое поле).
Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)

И это же уравнение в интегральной форме:

Циркуляция вектора напряжённости Е вихревого электрического поля (по любому замкнутому контуру) равняется скорости изменения магнитного потока через площадь контура (S) с противоположным знаком.
Уравнение 3: Закон Гаусса для магнетизма

И это же уравнение в интегральной форме:

Силовые линии магнитного поля замкнуты, т.к. поток вектора индукции В магнитного поля через любую замкнутую поверхность равняется нулю.
Уравнение 4: Закон Ампера

И это же уравнение в интегральной форме:

Циркуляция вектора напряжённости Н магнитного поля по замкнутому контуру равняется алгебраической сумме токов, которые пронизывают этот контур. Магнитное поле создаётся не только током проводимости, но и переменным электрическим полем.
Узнайте также про Напряжённость электрического поля, Резонанс и Магнитную индукцию.
 апряжённость
апряжённость апряжённость
апряжённость