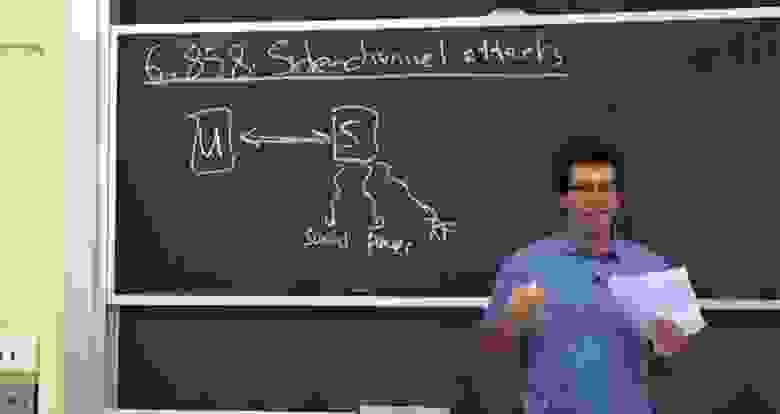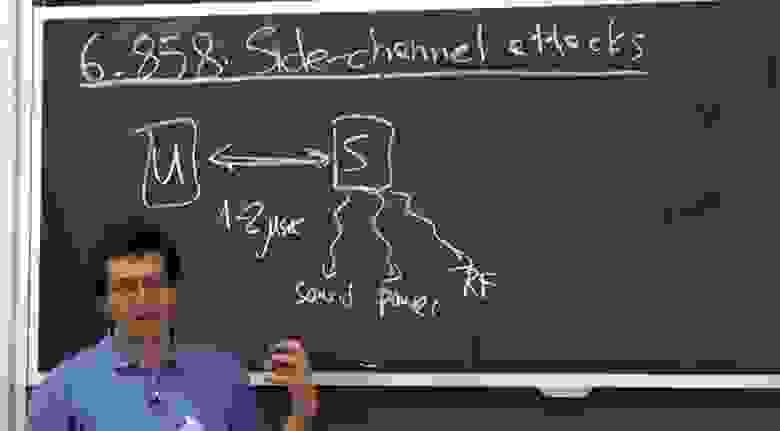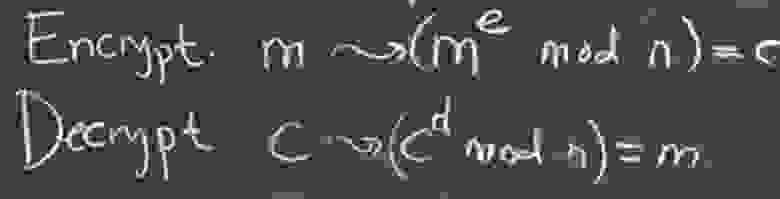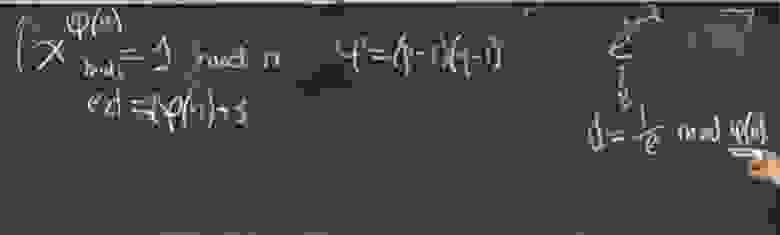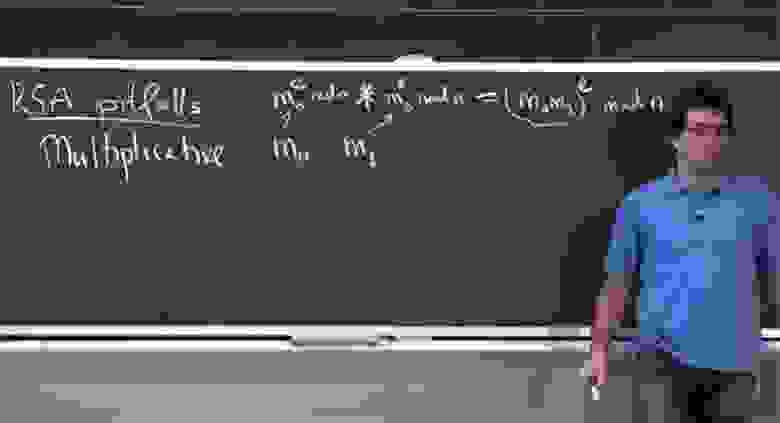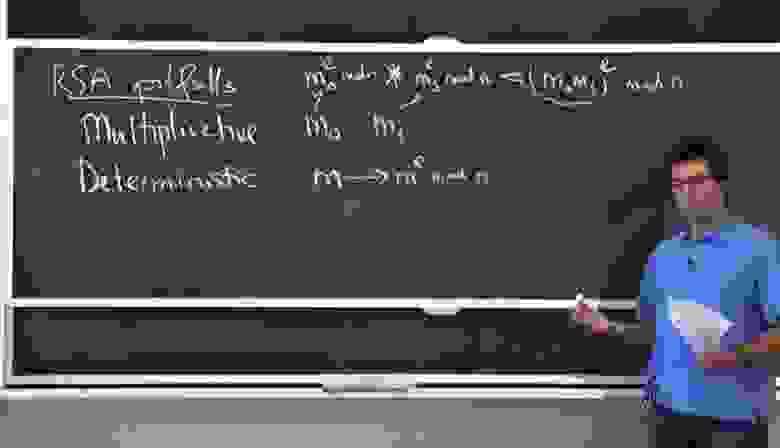Китайская теорема об остатках (CRT) RSA и множественные простые числа
Я написал код для облегчения вычисления больших чисел:
[email protected]:mrpre/bn_tool.git
Расчеты в этом фильме можно произвести с помощью этого инструмента.
Вычислить закрытый ключ открытого ключа RSA традиционным способом
Генерация закрытого ключа открытого ключа RSA
Два больших простых числа p, q, вычислить n = p * q
Вычислить phi (n), поскольку p и q — простые числа, поэтомуphi(n) = (p-1)*(q-1)
Возьмите случайное число e, взаимно простое с phi (n), и вычислите его элемент, обратный phi (n). То есть спросить d так, чтобы d удовлетворял
d*e = 1 mod (phi(n))。
(n, e) — открытый ключ, (n, d) — закрытый ключ
Используйте открытый ключ для шифрования и используйте закрытый ключ для дешифрования процесса (традиционный способ):
Расчет
Использовать шифрование с открытым ключом:
Чтобы зашифровать открытый текст m1, необходимо вычислитьc = m1^e mod n, C — зашифрованный текст.
Используйте закрытый ключ для расшифровки:
Чтобы расшифровать зашифрованный текст c, необходимо вычислитьm2 = c ^d mod n, m2 — открытый текст, то есть m2 = m1
Введение в китайскую теорему об остатках:
p и q — независимые большие простые числа, n равно p * q, для любого (m1, m2), (0 <= m1 <p, 0 <= m2 <p)
Должен быть уникальный m, 0 <= m <n
делает
m1 = m mod p
m2 = m mod q
Другими словами, при заданном a (m1, m2) должно существовать только m, удовлетворяющее вышеуказанному уравнению.
Итак, процесс расшифровки rsac^d mod n, Можно разложить наm1=c^d mod pтакже как иm2=c^d mod qУравнения, а затем вычислить m (метод вычисления m показан ниже).
, но уравнениеc ^ d mod p или c ^ d mod q , Хотя модуль был уменьшен с n до p или q, показатель степени d все еще относительно велик, и операция по-прежнему является дорогостоящей. Нам нужно понизить индекс.
Посмотрите внимательно на уравнениеc^d mod p
Сделать
d = k(p-1) + r
затем
c^d mod p
=c^(k(p-1) + r) mod p
=c^r * c^(k(p-1)) mod p
Поскольку c ^ (p-1) mod p = 1 (Теорема Эйлера)
=c^r mod pr — остаток от деления c на p-1, то есть r = d mod (p-1)
так что c^d mod pМожет быть уменьшено доc^(d mod p-1) mod p
Аналогичным образомc ^ d mod q сводится к c^(d mod q-1) mod q
среди них dp = d mod p-1 с участием dq = d mod q-1 Можно рассчитать заранее.
Но вычисление dp и dq может быть проще, то есть вычисление обратного значения e к p-1 и q-1 соответственно.
это (доказательство более сложное, если вы не понимаете, просто используйте егоd mod p-1с участиемd mod q-1В теме)
Процесс использования шифрования с открытым ключом и использования закрытого ключа для расшифровки (китайская оставшаяся теорема):
готово
Во-первых, нам нужно сгенерировать еще несколько чисел при генерации закрытого и открытого ключей:
Наш d является обратным элементом e к phi (n), теперь нам нужны два других обратных элемента (для (p-1) и (q-1)), И то и другое
1: вычислить dp так, чтобыdp*e = 1 mod(p-1)
2: вычислить dq так, чтобыdq*e = 1 mod(q-1)
Кроме того, необходим третий элемент, который является обратным q к p.
3: вычислить qInv так, чтобыqInv * q = 1 mod p
1 2 3 — все являются частью закрытого ключа.
Расчет
Использовать шифрование с открытым ключом:
Чтобы зашифровать открытый текст m, необходимо вычислитьc = m^e mod n, C — зашифрованный текст.
Используйте закрытый ключ для расшифровки:
1:m1=c^dp mod p
2:m2=c^dq mod q
3:h= (qInv*((m1 - m2)mod p)) mod p
4:m = m2 + h*q
m — простой текст.
например:
p=137
q=131
n = 137*131=17947
расчетphi(n) = 136*130=17680
Возьмите e = 3, вычислите обратное значение e к phi (n), d = 11787
Вы можете использовать мой инструмент для выполнения следующих команд
./a.out mod_inv "03" "2E0B"Я использовал алгоритм Евклида, чтобы найти здесь обратный элемент. Если вам интересно, вы можете изучить его подробно.
3*d = 1 mod 17680
3*d - 17680*x = 1
-17680 = -5893*3 - 1
решение1 d=-5893, x=-1
решение2 d=11787, x=2Для шифрования открытого текста 513
Используйте открытый ключ для шифрования и используйте закрытый ключ для дешифрования процесса (традиционный способ):
Зашифрованный текст513 ^ 3 mod 17947 = 8363
(можно использовать команду./a.out mod_exp "0201" "03" "461B")
Чтобы расшифровать зашифрованный текст 8363, необходимо вычислить8363^11787 mod 17947 = 513 , Расшифровка прошла успешно.
(можно использовать команду./a.out mod_exp "20AB" "2E0B" "461B")
Процесс использования шифрования с открытым ключом и использования закрытого ключа для расшифровки (китайская оставшаяся теорема):
предварительно рассчитано
dp = 91
dq = 87
qInv = 114
Затем расшифруйте c = 8363 и выполните следующие вычисления:
m1 = c^dp mod p = 102
m2 = c^dq mod q = 120
h = (qInv*((m1 - m2)modp))mod p
= (114*(-18 mod 137)) mod 137
= 114*119 mod 137
= 3
m = m2 + h*q = 120 + 3*131 = 513Множественные простые числа
Чтобы подчеркнуть особенность нескольких простых чисел, мы называем сертификат RSA в приведенном выше примере сертификатом одного простого числа (на самом деле такого имени нет).
Генерация открытого ключа
p=137
q=131
r=127
Расчетn=p*q*r=2279269
расчетphi(n)=136*130*126=2227680
Возьмите e = 19 и вычислите элемент, обратный e к phi (n). То есть спросить d так, чтобы d удовлетворялd*19= 1 mod phi(n)
d=351739
(можно использовать команду./a.out mod_inv "13" "21FDE0")
Открытый ключ (2279269, 19)
закрытый ключ (2279269, 351739)
Шифрование открытым ключом и расшифровка закрытым ключом (традиционный способ):
Чтобы зашифровать 513,
513^19 mod 2279269 = 768924
(можно использовать команду./a.out mod_exp "0201" "13" "22C765")
Чтобы расшифровать 768924,
768924^351739 mod 2279269 = 513
(можно использовать команду./a.out mod_exp "0BBB9C" "055DFB" "22C765")
Этот расчет такой же, как и для сертификата с одним простым числом. Но это глупо, доступно много простых чисел, почему бы и нет?
Используйте шифрование с открытым ключом и используйте закрытый ключ для дешифрования (китайская теорема об остатках для нескольких простых чисел):
Предварительно рассчитано:
dp = 19^-1 mod 137-1 = 43
dq = 19^-1 mod 131-1 = 89
dr = 19^-1 mod 127-1 = 73
Чтобы расшифровать зашифрованный текст 768924, сначала вычислите
1:m1=768924^43 mod 137 = 102
2:m2=768924^89 mod 131 = 120
3:m3=768924^73 mod 127 = 5
Расчет непрерывных уравнений по уравнениям 1 и 2:
qInv = 114(Рассчитывается заранее)
h = (qInv*((m1 - m2)mod p)) mod p
= (114*(-18 mod 137) mod 137 ) mod 137
= 3
m12 = m2 + h*q = 120 + 3*131 = 513Общее решение 1 и 2:
513+k1*(131*137)
После объединения уравнений 1 и 2 и добавления уравнения 3 проблема преобразуется в:
m1=513 p=17947
m2=5 q=127Вычислите величину, обратную q к p qInv = 10316
h = (10316*((513 - 5)mod 17947)) mod 17947
= 4
m = 5 + 4*127 = 513Преимущества сертификатов с несколькими простыми числами
Для достижения одинаковой длины n, n можно разложить на несколько маленьких простых чисел; чем больше маленьких простых чисел, тем меньше значение p, q, r, … rn. Чем быстрее используется китайская теорема об остатках.
Сертификат на несколько простых чисел
Закрытый ключ — это многопозиционный сертификат, который является многопозиционным сертификатом. . . . .
Рассмотрим систему
сравнений
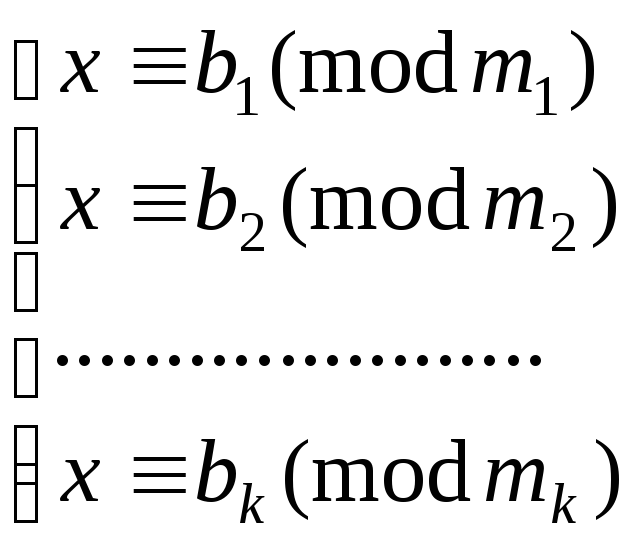
От системы сравнений
вида aix
≡ bi
(mod
mi)
можно перейти к данной способом,
указанным в п.1.
Китайская
теорема об остатках (I
век до н.э. Сунь-Цзе)
Пусть m1,…,
mk
– попарно простые числа
система
сравнений (*) имеет единственное решение
x0
≡
**,
где M=,
Mi=,
.
Доказательство:
Т.к. msMj
система (*)
равносильна системе
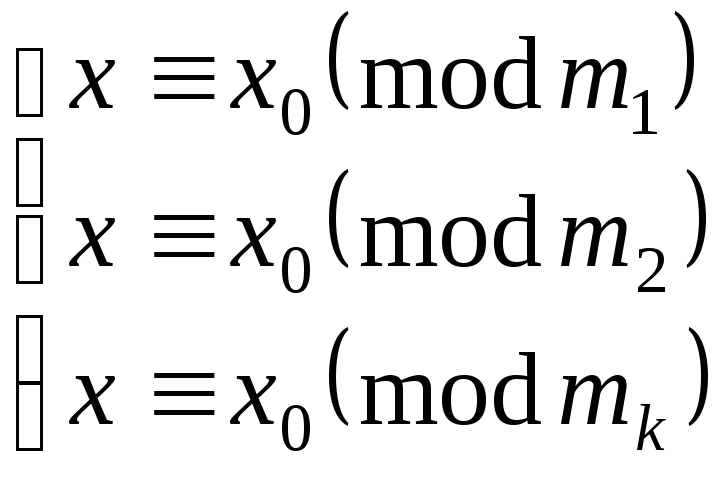
т.е. системам (*) и
(***) удовлетворяют одни и те же значения
x.
Системе (***) (в силу свойств 12 и 13 сравнений)
удовлетворяют те и только те значения,
которые заданы теоремой (т.е. x0).
□
Следствие.
Если в системе **
независимо друг от друга пробегают
полные системы вычетов по модулямсоответственно, то
пробегает полную систему вычетов по
модулюM.
Доказательство:
в силу свойства 13 сравнений, x0
пробегает ровно M
не сравнимых по модулю M
значений.
□
Пример
Решить систему
сравнений:
|
mi |
3 |
4 |
5 |
|
Mi |
20 |
15 |
12 |
|
|
2 |
3 |
3 |
Вычислим параметры,
необходимые для нахождения решения.
Составим таблицу
Согласно китайской
теореме об остатках, решением будет
являться
x0≡1∙20∙2+2∙15∙3+4∙12∙3(mod
60)≡40+90+144(mod
60)≡34(mod
60).
Ответ:
x≡34(mod
60).
Проверка:
Решение верно.
4.3. Применения китайской теоремы об остатках.
Китайская теорема
об остатках находит широкое применение
в теории чисел и криптографии.
Применение
Китайской теоремы об остатках в
криптосистеме RSA.
В криптосистеме
RSA
при расшифровании требуется вычислить
ydmod
n,
причем известно, что n=p∙q,
где p,
q
– большие простые числа. Как было
показано ранее, степень d,
в которую требуется возвести шифрованный
текст, можно понизить за счет использования
теоремы Эйлера. Зная разложение числа
n
на простые сомножители и используя
китайскую теорему об остатках, возможно
еще более ускорить вычисления.
Сначала вычисляют:
r1=yd
mod
p=(y
mod
p)d
mod
(p–1)mod
p,
r2=yd
mod
q=(y
mod q)d
mod (q–1)mod
q.
Как читатель мог
заметить, при вычислениях для ускорения
возведения в степень используется
теорема Ферма.
Получим систему
сравнений
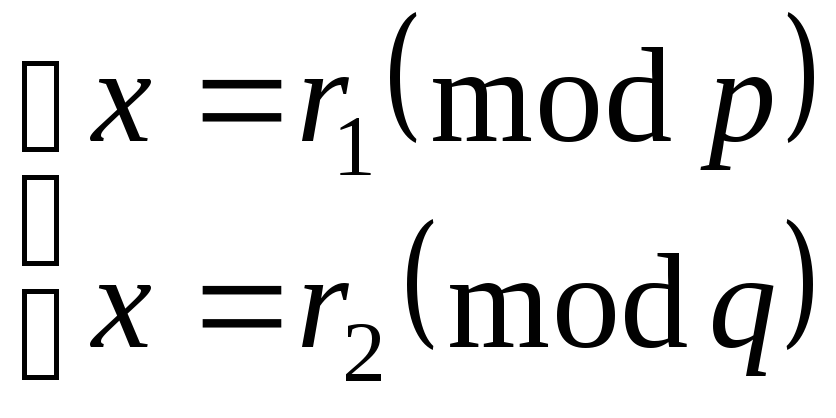
Решая ее по
китайской теореме об остатках, получим
решение
.
Сложность возведения
в степень с использованием китайской
теоремы об остатках и теоремы Ферма
составляет около
6k3
против 24k3
при
использовании только теоремы Ферма
(где k
есть размерность числа
n).
Пример.
Пусть в RSA
Требуется вычислить
x=10029
mod
187.
Вычисляем:
r1=(100
mod 11)29
mod 10 mod
11=19
mod 11 = 1,
r2=(100
mod 17)29
mod 16
mod 17=1513
mod
17=2.
Cоставляем
систему
Пользуясь Китайской
теоремой об остатках, решаем эту систему.
-
mi
11
17
Mi
17
11
M’i
2
14
Получаем
Ответ: 10029
mod
187=155.
Схема разделения
секрета на основе Китайской теоремы
об остатках.
На основе китайской
теоремы об остатках можно построить
(n,k)–пороговую
схему разделения секрета. Напомним
основные принципы схем разделения
секрета.
Пусть существует
некая информация, которую следует
сохранить в секрете, и имеется n
участников, не доверяющих друг другу.
Эти участники хотят, чтобы секретную
информацию можно было получить только
при условии того, что как минимум k
участников из n
собрались вместе.
(n,k)-пороговая
схема разделения секрета
– это схема разделения секретной
информации между n
участниками таким образом, чтобы только
k
из них (или более), собравшись вместе,
могли получить этот секрет. Причем
вероятность угадать верное значение
секрета при наличии k–m
долей секрета
m>0
равна вероятности угадать верное
значение секрета без обладания долей
секрета. При этом все участники протокола
равноправны.
Как правило, схемы
разделения секрета состоят из 2-х фаз:
фазы разделения, когда каждому участнику
протокола выдается его доля секрета,
и фаза восстановления, когда k
или более любых участников, собрав свои
доли, восстанавливают общий секрет.
Схема разделения
секрета на основе китайской теоремы
об остатках выглядит следующим образом:
Пусть
N
– общий секрет.
Разделение
секрета:
Берем p1,
p2,…,
pn
– различные простые числа.
Часть секрета,
выдаваемая i-му
участнику схемы, есть число xi,
вычисляемое как xi≡N(mod
pi).
Заметим, что числа
p1,
p2,…,
pn
должны быть такими, чтобы произведение
любых k
из них было больше, чем N.
А это достигается, когда для всех i
выполняется pi>.
Для того, чтобы
k–1
участников не смогли восстановить
секрет без k-го
участника, необходимо, чтобы pi
<<
.
Итак, относительно
чисел p1,
p2,…,
pn
должны
выполняться условия:
<
pi
<<
.
Восстановление
секрета:
Собравшись вместе,
k
участников составляют и решают систему
сравнений
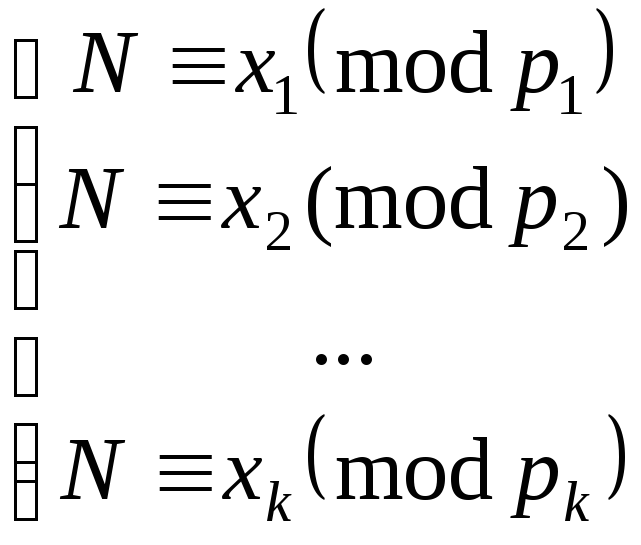
Решив систему,
участники получают общий секрет N.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Prerequisite : RSA Algorithm
Why RSA decryption is slow ?
RSA decryption is slower than encryption because while doing decryption, private key parameter ” d ” is necessarily large. Moreover the parameters – ” p and q ” are two very large Prime Numbers.
Given integers c, e, p and q, find m such that c = pow(m, e) mod (p * q) (RSA decryption for weak integers).
Basics :
- RSA is a public key encryption system used for secure transmission of messages.
- RSA involves four steps typically :
(1) Key generation
(2) Key distribution
(3) Encryption
(4) Decryption- Message Encryption is done with a “Public Key”.
- Message Decryption is done with a “Private Key” – parameters (p, q, d) generated along with Public Key.
- The private key is known only to the user, and the public key can be made known to anyone who wishes to send an encrypted message to the person with the corresponding private key.
- A public key which is depicted by two parameters n (modulus) and e (exponent). The modulus is a product of two very large prime numbers (p and q as shown below). Decryption of this message would require the user to factorize n into two prime factors(the main reason, RSA is secure), and then find the modular inverse of e, wherein the difficult task lies.
- A text message is first converted to the respective decimal value, which is the parameter ‘m’ which we are finding below. We now encrypt this message by doing c = pow(m, e) mod (p * q), where c is the encrypted text.
In this code, we exploit weak modulus and exponent values to try and crack the encryption by generating the private key by finding the values of p, q and d. In these examples, we will try to find d given p and q.
NOTE :
Here, in this example we are using small values of p and q but in actual we use very large values of p and q to make our RSA system secure.
Examples :
Input : c = 1614 e = 65537 p = 53 q = 31 Output : 1372 Explanation : We calculate c = pow(m, e)mod(p * q). Insert m = 1372. On calculating, we get c = 1614. Input : c = 3893595 e = 101 p = 3191 q = 3203 Output : 6574839 Explanation : As shown above, if we calculate pow(m, e)mod(p * q) with m = 6574839, we get c = 3893595
Normally, we can find the value of m by following these steps:
(1) Calculate the modular inverse of e.
We can make use of the following equation, d = e^(-1)(mod lambda(n)),
where lambda is the Carmichael Totient function.
Read: Carmichael function(2) Calculate m = pow(c, d)mod(p * q)
(3) We can perform this calculation faster by using the Chinese Remainder Theorem,
as defined below in the function
Further reading on Chinese Remainder Theorem can be done at
RSA (cryptosystem)
Below is the Python implementation of this approach :
def gcd(p, q):
if q == 0:
return p
return gcd(q, p % q)
def lcm(p, q):
return p * q / gcd(p, q)
def egcd(e, phi):
if e == 0:
return (phi, 0, 1)
else:
g, y, x = egcd(phi % e, e)
return (g, x - (phi // e) * y, y)
def modinv(e, phi):
g, x, y = egcd(e, phi)
return x % phi
def chineseremaindertheorem(dq, dp, p, q, c):
m1 = pow(c, dp, p)
m2 = pow(c, dq, q)
qinv = modinv(q, p)
h = (qinv * (m1 - m2)) % p
m = m2 + h * q
return m
p = 9817
q = 9907
e = 65537
c = 36076319
d = modinv(e, lcm(p - 1, q - 1))
dq = pow(d, 1, q - 1)
dp = pow(d, 1, p - 1)
print chineseremaindertheorem(dq, dp, p, q, c)
Output :
41892906
Sun-tzu’s original formulation: x ≡ 2 (mod 3) ≡ 3 (mod 5) ≡ 2 (mod 7) with the solution x = 23 + 105k, with k an integer
In mathematics, the Chinese remainder theorem states that if one knows the remainders of the Euclidean division of an integer n by several integers, then one can determine uniquely the remainder of the division of n by the product of these integers, under the condition that the divisors are pairwise coprime (no two divisors share a common factor other than 1).
For example, if we know that the remainder of n divided by 3 is 2, the remainder of n divided by 5 is 3, and the remainder of n divided by 7 is 2, then without knowing the value of n, we can determine that the remainder of n divided by 105 (the product of 3, 5, and 7) is 23. Importantly, this tells us that if n is a natural number less than 105, then 23 is the only possible value of n.
The earliest known statement of the theorem is by the Chinese mathematician Sun-tzu in the Sun-tzu Suan-ching in the 3rd century CE.
The Chinese remainder theorem is widely used for computing with large integers, as it allows replacing a computation for which one knows a bound on the size of the result by several similar computations on small integers.
The Chinese remainder theorem (expressed in terms of congruences) is true over every principal ideal domain. It has been generalized to any ring, with a formulation involving two-sided ideals.
History[edit]
The earliest known statement of the theorem, as a problem with specific numbers, appears in the 3rd-century book Sun-tzu Suan-ching by the Chinese mathematician Sun-tzu:[1]
There are certain things whose number is unknown. If we count them by threes, we have two left over; by fives, we have three left over; and by sevens, two are left over. How many things are there?[2]
Sun-tzu’s work contains neither a proof nor a full algorithm.[3] What amounts to an algorithm for solving this problem was described by Aryabhata (6th century).[4] Special cases of the Chinese remainder theorem were also known to Brahmagupta (7th century), and appear in Fibonacci’s Liber Abaci (1202).[5] The result was later generalized with a complete solution called Da-yan-shu (大衍術) in Ch’in Chiu-shao’s 1247 Mathematical Treatise in Nine Sections (數書九章, Shu-shu Chiu-chang)[6] which was translated into English in early 19th century by British missionary Alexander Wylie.[7]
The notion of congruences was first introduced and used by Carl Friedrich Gauss in his Disquisitiones Arithmeticae of 1801.[9] Gauss illustrates the Chinese remainder theorem on a problem involving calendars, namely, «to find the years that have a certain period number with respect to the solar and lunar cycle and the Roman indiction.»[10] Gauss introduces a procedure for solving the problem that had already been used by Leonhard Euler but was in fact an ancient method that had appeared several times.[11]
Statement[edit]
Let n1, …, nk be integers greater than 1, which are often called moduli or divisors. Let us denote by N the product of the ni.
The Chinese remainder theorem asserts that if the ni are pairwise coprime, and if a1, …, ak are integers such that 0 ≤ ai < ni for every i, then there is one and only one integer x, such that 0 ≤ x < N and the remainder of the Euclidean division of x by ni is ai for every i.
This may be restated as follows in terms of congruences:
If the 
has a solution, and any two solutions, say x1 and x2, are congruent modulo N, that is, x1 ≡ x2 (mod N ).[12]
In abstract algebra, the theorem is often restated as: if the ni are pairwise coprime, the map
defines a ring isomorphism[13]
between the ring of integers modulo N and the direct product of the rings of integers modulo the ni. This means that for doing a sequence of arithmetic operations in 

The theorem can also be restated in the language of combinatorics as the fact that the infinite arithmetic progressions of integers form a Helly family.[14]
Proof[edit]
The existence and the uniqueness of the solution may be proven independently. However, the first proof of existence, given below, uses this uniqueness.
Uniqueness[edit]
Suppose that x and y are both solutions to all the congruences. As x and y give the same remainder, when divided by ni, their difference x − y is a multiple of each ni. As the ni are pairwise coprime, their product N also divides x − y, and thus x and y are congruent modulo N. If x and y are supposed to be non-negative and less than N (as in the first statement of the theorem), then their difference may be a multiple of N only if x = y.
Existence (first proof)[edit]
The map
maps congruence classes modulo N to sequences of congruence classes modulo ni. The proof of uniqueness shows that this map is injective. As the domain and the codomain of this map have the same number of elements, the map is also surjective, which proves the existence of the solution.
This proof is very simple but does not provide any direct way for computing a solution. Moreover, it cannot be generalized to other situations where the following proof can.
Existence (constructive proof)[edit]
Existence may be established by an explicit construction of x.[15] This construction may be split into two steps, first solving the problem in the case of two moduli, and then extending this solution to the general case by induction on the number of moduli.
Case of two moduli[edit]
We want to solve the system:
where 

Bézout’s identity asserts the existence of two integers 

The integers 

A solution is given by
Indeed,
implying that 
General case[edit]
Consider a sequence of congruence equations:
where the 

As the other 


Existence (direct construction)[edit]
For constructing a solution, it is not necessary to make an induction on the number of moduli. However, such a direct construction involves more computation with large numbers, which makes it less efficient and less used. Nevertheless, Lagrange interpolation is a special case of this construction, applied to polynomials instead of integers.
Let 





A solution of the system of congruences is
In fact, as 

we have
for every 
Computation[edit]
Consider a system of congruences:
where the 



Several methods of computation are presented. The two first ones are useful for small examples, but become very inefficient when the product 

Systematic search[edit]
It is easy to check whether a value of x is a solution: it suffices to compute the remainder of the Euclidean division of x by each ni. Thus, to find the solution, it suffices to check successively the integers from 0 to N until finding the solution.
Although very simple, this method is very inefficient. For the simple example considered here, 40 integers (including 0) have to be checked for finding the solution, which is 39. This is an exponential time algorithm, as the size of the input is, up to a constant factor, the number of digits of N, and the average number of operations is of the order of N.
Therefore, this method is rarely used, neither for hand-written computation nor on computers.
Search by sieving[edit]
The smallest two solutions, 23 and 128, of the original formulation of the Chinese remainder theorem problem found using a sieve
The search of the solution may be made dramatically faster by sieving. For this method, we suppose, without loss of generality, that 


By testing the values of these numbers modulo 

Testing the values of these numbers modulo 
This method is faster if the moduli have been ordered by decreasing value, that is if 
- 4 mod 4 → 0. Continue
- 4 + 5 = 9 mod 4 →1. Continue
- 9 + 5 = 14 mod 4 → 2. Continue
- 14 + 5 = 19 mod 4 → 3. OK, continue by considering remainders modulo 3 and adding 5 × 4 = 20 each time
- 19 mod 3 → 1. Continue
- 19 + 20 = 39 mod 3 → 0. OK, this is the result.
This method works well for hand-written computation with a product of moduli that is not too big. However, it is much slower than other methods, for very large products of moduli. Although dramatically faster than the systematic search, this method also has an exponential time complexity and is therefore not used on computers.
Using the existence construction[edit]
The constructive existence proof shows that, in the case of two moduli, the solution may be obtained by the computation of the Bézout coefficients of the moduli, followed by a few multiplications, additions and reductions modulo 




For more than two moduli, the method for two moduli allows the replacement of any two congruences by a single congruence modulo the product of the moduli. Iterating this process provides eventually the solution with a complexity, which is quadratic in the number of digits of the product of all moduli. This quadratic time complexity does not depend on the order in which the moduli are regrouped. One may regroup the two first moduli, then regroup the resulting modulus with the next one, and so on. This strategy is the easiest to implement, but it also requires more computation involving large numbers.
Another strategy consists in partitioning the moduli in pairs whose product have comparable sizes (as much as possible), applying, in parallel, the method of two moduli to each pair, and iterating with a number of moduli approximatively divided by two. This method allows an easy parallelization of the algorithm. Also, if fast algorithms (that is, algorithms working in quasilinear time) are used for the basic operations, this method provides an algorithm for the whole computation that works in quasilinear time.
On the current example (which has only three moduli), both strategies are identical and work as follows.
Bézout’s identity for 3 and 4 is
Putting this in the formula given for proving the existence gives
for a solution of the two first congruences, the other solutions being obtained by adding to −9 any multiple of 3 × 4 = 12. One may continue with any of these solutions, but the solution 3 = −9 +12 is smaller (in absolute value) and thus leads probably to an easier computation
Bézout identity for 5 and 3 × 4 = 12 is
Applying the same formula again, we get a solution of the problem:
The other solutions are obtained by adding any multiple of 3 × 4 × 5 = 60, and the smallest positive solution is −21 + 60 = 39.
As a linear Diophantine system[edit]
The system of congruences solved by the Chinese remainder theorem may be rewritten as a system of linear Diophantine equations:
where the unknown integers are 

Over principal ideal domains[edit]
In § Statement, the Chinese remainder theorem has been stated in three different ways: in terms of remainders, of congruences, and of a ring isomorphism. The statement in terms of remainders does not apply, in general, to principal ideal domains, as remainders are not defined in such rings. However, the two other versions make sense over a principal ideal domain R: it suffices to replace «integer» by «element of the domain» and 
However, in general, the theorem is only an existence theorem and does not provide any way for computing the solution, unless one has an algorithm for computing the coefficients of Bézout’s identity.
Over univariate polynomial rings and Euclidean domains[edit]
The statement in terms of remainders given in § Theorem statement cannot be generalized to any principal ideal domain, but its generalization to Euclidean domains is straightforward. The univariate polynomials over a field is the typical example of a Euclidean domain which is not the integers. Therefore, we state the theorem for the case of the ring ![{displaystyle R=K[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3fe87f64d3fb94108c78a00de91e770e01ea465)

The Chinese remainder theorem for polynomials is thus: Let 

![{displaystyle R=K[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3fe87f64d3fb94108c78a00de91e770e01ea465)



If 







The construction of the solution may be done as in § Existence (constructive proof) or § Existence (direct proof). However, the latter construction may be simplified by using, as follows, partial fraction decomposition instead of the extended Euclidean algorithm.
Thus, we want to find a polynomial 
for 
Consider the polynomials
The partial fraction decomposition of 


and thus
Then a solution of the simultaneous congruence system is given by the polynomial
In fact, we have
for 
This solution may have a degree larger than 




Lagrange interpolation[edit]
A special case of Chinese remainder theorem for polynomials is Lagrange interpolation. For this, consider k monic polynomials of degree one:
They are pairwise coprime if the 



Now, let 



for every 
Lagrange interpolation formula is exactly the result, in this case, of the above construction of the solution. More precisely, let
The partial fraction decomposition of 
In fact, reducing the right-hand side to a common denominator one gets
and the numerator is equal to one, as being a polynomial of degree less than 


Using the above general formula, we get the Lagrange interpolation formula:
Hermite interpolation[edit]
Hermite interpolation is an application of the Chinese remainder theorem for univariate polynomials, which may involve moduli of arbitrary degrees (Lagrange interpolation involves only moduli of degree one).
The problem consists of finding a polynomial of the least possible degree, such that the polynomial and its first derivatives take given values at some fixed points.
More precisely, let 











Consider the polynomial
This is the Taylor polynomial of order 


Conversely, any polynomial 


therefore 



The Chinese remainder theorem asserts that there exists exactly one polynomial of degree less than the sum of the 

There are several ways for computing the solution 
Generalization to non-coprime moduli[edit]
The Chinese remainder theorem can be generalized to non-coprime moduli. Let 


If 

If one uses Bézout’s identity to write 
This defines an integer, as g divides both m and n. Otherwise, the proof is very similar to that for coprime moduli.
Generalization to arbitrary rings[edit]
The Chinese remainder theorem can be generalized to any ring, by using coprime ideals (also called comaximal ideals). Two ideals I and J are coprime if there are elements 


Let I1, …, Ik be two-sided ideals of a ring 
between the quotient ring 
where «

Moreover, if 
if Ii and Ij are coprime for all i ≠ j.
Interpretation in terms of idempotents[edit]
Let 

be the isomorphism defined above. Let 


The 




In summary, this generalized Chinese remainder theorem is the equivalence between giving pairwise coprime two-sided ideals with a zero intersection, and giving central and pairwise orthogonal idempotents that sum to 1.[18]
Applications[edit]
Sequence numbering[edit]
The Chinese remainder theorem has been used to construct a Gödel numbering for sequences, which is involved in the proof of Gödel’s incompleteness theorems.
Fast Fourier transform[edit]
The prime-factor FFT algorithm (also called Good-Thomas algorithm) uses the Chinese remainder theorem for reducing the computation of a fast Fourier transform of size 




Encryption[edit]
Most implementations of RSA use the Chinese remainder theorem during signing of HTTPS certificates and during decryption.
The Chinese remainder theorem can also be used in secret sharing, which consists of distributing a set of shares among a group of people who, all together (but no one alone), can recover a certain secret from the given set of shares. Each of the shares is represented in a congruence, and the solution of the system of congruences using the Chinese remainder theorem is the secret to be recovered. Secret sharing using the Chinese remainder theorem uses, along with the Chinese remainder theorem, special sequences of integers that guarantee the impossibility of recovering the secret from a set of shares with less than a certain cardinality.
Range ambiguity resolution[edit]
The range ambiguity resolution techniques used with medium pulse repetition frequency radar can be seen as a special case of the Chinese remainder theorem.
Decomposition of surjections of finite abelian groups[edit]
Given a surjection 
where 
from the original surjection, we have 


can be defined if 

These observations are pivotal for constructing the ring of profinite integers, which is given as an inverse limit of all such maps.
Dedekind’s theorem[edit]
Dedekind’s theorem on the linear independence of characters. Let M be a monoid and k an integral domain, viewed as a monoid by considering the multiplication on k. Then any finite family ( fi )i∈I of distinct monoid homomorphisms fi : M → k is linearly independent. In other words, every family (αi)i∈I of elements αi ∈ k satisfying
must be equal to the family (0)i∈I.
Proof. First assume that k is a field, otherwise, replace the integral domain k by its quotient field, and nothing will change. We can linearly extend the monoid homomorphisms fi : M → k to k-algebra homomorphisms Fi : k[M] → k, where k[M] is the monoid ring of M over k. Then, by linearity, the condition
yields
Next, for i, j ∈ I; i ≠ j the two k-linear maps Fi : k[M] → k and Fj : k[M] → k are not proportional to each other. Otherwise fi and fj would also be proportional, and thus equal since as monoid homomorphisms they satisfy: fi (1) = 1 = fj (1), which contradicts the assumption that they are distinct.
Therefore, the kernels Ker Fi and Ker Fj are distinct. Since k[M]/Ker Fi ≅ Fi (k[M]) = k is a field, Ker Fi is a maximal ideal of k[M] for every i in I. Because they are distinct and maximal the ideals Ker Fi and Ker Fj are coprime whenever i ≠ j. The Chinese Remainder Theorem (for general rings) yields an isomorphism:
where
Consequently, the map
is surjective. Under the isomorphisms k[M]/Ker Fi → Fi (k[M]) = k, the map Φ corresponds to:
Now,
yields
for every vector (ui)i∈I in the image of the map ψ. Since ψ is surjective, this means that
for every vector
Consequently, (αi)i∈I = (0)i∈I. QED.
See also[edit]
- Covering system
- Hasse principle
- Residue number system
Notes[edit]
- ^ Katz 1998, p. 197
- ^ Dence & Dence 1999, p. 156
- ^ Dauben 2007, p. 302
- ^ Kak 1986
- ^ Pisano 2002, pp. 402–403
- ^ Dauben 2007, p. 310
- ^ Libbrecht 1973
- ^ Gauss 1986, Art. 32–36
- ^ Ireland & Rosen 1990, p. 36
- ^ Ore 1988, p. 247
- ^ Ore 1988, p. 245
- ^ Ireland & Rosen 1990, p. 34
- ^ Ireland & Rosen 1990, p. 35
- ^ Duchet 1995
- ^ Rosen 1993, p. 136
- ^ Ireland & Rosen 1990, p. 181
- ^ Sengupta 2012, p. 313
- ^ Bourbaki, N. 1989, p. 110
References[edit]
- Dauben, Joseph W. (2007), «Chapter 3: Chinese Mathematics», in Katz, Victor J. (ed.), The Mathematics of Egypt, Mesopotamia, China, India and Islam : A Sourcebook, Princeton University Press, pp. 187–384, ISBN 978-0-691-11485-9
- Dence, Joseph B.; Dence, Thomas P. (1999), Elements of the Theory of Numbers, Academic Press, ISBN 9780122091308
- Duchet, Pierre (1995), «Hypergraphs», in Graham, R. L.; Grötschel, M.; Lovász, L. (eds.), Handbook of combinatorics, Vol. 1, 2, Amsterdam: Elsevier, pp. 381–432, MR 1373663. See in particular Section 2.5, «Helly Property», pp. 393–394.
- Gauss, Carl Friedrich (1986), Disquisitiones Arithemeticae, translated by Clarke, Arthur A. (Second, corrected ed.), New York: Springer, ISBN 978-0-387-96254-2
- Ireland, Kenneth; Rosen, Michael (1990), A Classical Introduction to Modern Number Theory (2nd ed.), Springer-Verlag, ISBN 0-387-97329-X
- Kak, Subhash (1986), «Computational aspects of the Aryabhata algorithm» (PDF), Indian Journal of History of Science, 21 (1): 62–71
- Katz, Victor J. (1998), A History of Mathematics / An Introduction (2nd ed.), Addison Wesley Longman, ISBN 978-0-321-01618-8
- Libbrecht, Ulrich (1973), Chinese Mathematics in the Thirteenth Century: the «Shu-shu Chiu-chang» of Ch’in Chiu-shao, Dover Publications Inc, ISBN 978-0-486-44619-6
- Ore, Oystein (1988) [1948], Number Theory and Its History, Dover, ISBN 978-0-486-65620-5
- Pisano, Leonardo (2002), Fibonacci’s Liber Abaci, translated by Sigler, Laurence E., Springer-Verlag, pp. 402–403, ISBN 0-387-95419-8
- Rosen, Kenneth H. (1993), Elementary Number Theory and its Applications (3rd ed.), Addison-Wesley, ISBN 978-0201-57889-8
- Sengupta, Ambar N. (2012), Representing Finite Groups, A Semimsimple Introduction, Springer, ISBN 978-1-4614-1232-8
- Bourbaki, N. (1989). Algebra I. Springer. ISBN 3-540-64243-9.
Further reading[edit]
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001), Introduction to Algorithms (Second ed.), MIT Press and McGraw-Hill, ISBN 0-262-03293-7. See Section 31.5: The Chinese remainder theorem, pp. 873–876.
- Ding, Cunsheng; Pei, Dingyi; Salomaa, Arto (1996), Chinese Remainder Theorem: Applications in Computing, Coding, Cryptography, World Scientific Publishing, pp. 1–213, ISBN 981-02-2827-9
- Hungerford, Thomas W. (1974), Algebra, Graduate Texts in Mathematics, Vol. 73, Springer-Verlag, pp. 131–132, ISBN 978-1-4612-6101-8
- Knuth, Donald (1997), The Art of Computer Programming, vol. 2: Seminumerical Algorithms (Third ed.), Addison-Wesley, ISBN 0-201-89684-2. See Section 4.3.2 (pp. 286–291), exercise 4.6.2–3 (page 456).
External links[edit]
- «Chinese remainder theorem», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Weisstein, Eric W. «Chinese Remainder Theorem». MathWorld.
- Chinese Remainder Theorem at PlanetMath.
- Full text of the Sun-tzu Suan-ching (Chinese) – Chinese Text Project
Курсовая работа
по дисциплине «Алгебра»
на тему: «Китайская
Теорема об остатках и её следствия»
Оглавление
Введение
Глава 1. Элементарная теория сравнений, а ≡ b (mod p)
. Определения и основные свойства сравнений
. Теорема Эйлера, теорема Ферма
Глава 2. Китайская теорема об остатках
. Китайская теорема об остатках (КТО)
. Примеры. Применение к решению олимпиадных задач
. КТО. Применение к открытию сейфа в банке
Заключение
Список литературы
Введение
Первоначальные элементы
математики связаны с появлением навыков счета, возникающих в примитивной форме
на сравнительно ранних ступенях развития человеческого общества в процессе
трудовой деятельности. Понятие натурального числа, появляющееся как результат
постепенного абстрагирования, является основой всего дальнейшего развития
математики. В теории чисел, естественно, выделяются и рассматриваются в первую
очередь те проблемы, которые глубоко и достаточно непосредственно связаны с
изучаемыми объектами и важны для построения математики в ее целом. Некоторые
теоретико-числовые задачи возникают уже в рамках школьного курса арифметики.
Исторически теория чисел возникла как непосредственное развитие арифметики. В
настоящее время в теорию чисел включают значительно более широкий круг
вопросов, выходящих за рамки изучения натуральных чисел. В теории чисел
рассматриваются не только натуральные числа, но и множество всех целых чисел, а
также множество рациональных чисел.
Современную теорию чисел
можно в основном разбить на следующие разделы:
) Элементарная теория
чисел (теория сравнений, теория форм, неопределенные уравнения). К этому
разделу относят вопросы теории чисел, являющиеся непосредственным развитием
теории делимости, и вопросы о представимости чисел в определенной форме. Более
общей является задача решения систем неопределенных уравнений, т. е. уравнений,
в которых значения неизвестных должны быть обязательно целыми числами.
Неопределенные уравнения называют также диофантовыми уравнениями, так как
Диофант был первым математиком, систематически рассматривавшим такие уравнения.
Мы условно называем этот раздел „Элементарная теория чисел», поскольку
здесь часто применяются обычные арифметические и алгебраические методы
исследования.
) Алгебраическая теория
чисел. К этому разделу относят вопросы, связанные с изучением различных классов
алгебраических чисел.
) Диофантовы приближения.
К этому разделу относят вопросы, связанные с изучением приближения
действительных чисел рациональными дробями. К диофантовым приближениям
примыкают тесно связанные с этим же кругом идей вопросы изучения арифметической
природы различных классов чисел.
) Аналитическая теория
чисел. К этому разделу относят вопросы теории чисел, для изучения которых
приходится применять методы математического анализа.
В данной курсовой работе
мы столкнемся с элементарной теорией чисел, а точнее с элементарной теорией
сравнений, её основными свойствами и определениями, которые будут рассмотрены в
первой главе.
Во второй главе будет
рассмотрен один из важных результатов теории чисел, так называемая китайская
теорема об остатках (KTO). По существу эта теорема утверждает, что можно
восстановить целое число по множеству его остатков от деления на числа из
некоторого набора попарно взаимно простых чисел. Эта теорема в её
арифметической формулировке была описана в трактате китайского математика Сунь
Цзы «Сунь Цзы Суань Цзин» (кит.упр.孙子算经, пиньинь: sunzi suanjing), предположительно датируемом третьим
веком н. э. и затем была обобщена Цинь Цзюшао в его книге «Математические
рассуждения в 9 главах» датируемой 1247 годом.
Китайская теорема об
остатках широко применяется в теории чисел, криптографии и других дисциплинах:
. Взаимно
однозначное соответствие между некоторым числом и набором его остатков,
определяемым набором взаимно простых чисел, существование которого утверждается
в теореме, на практике помогает работать не с длинными числами, а с наборами их
коротких по длине остатков. Кроме того вычисления по каждому из модулей можно
выполнять параллельно. Если в качестве базиса взять, к примеру, первые 500
простых чисел, длина каждого из которых не превосходит 12 бит, то этого хватит
для представления десятичных чисел длиной до 1519 знаков. (Откуда взялось число
1519 понять очень просто: сумма десятичных логарифмов первых 500 простых чисел
равна 1519,746…). Например, в алгоритме RSA вычисления производятся по модулю очень большого числа n, представимого в виде
произведения двух больших простых чисел. Теорема позволяет перейти к
вычислениям по модулю этих простых делителей, которые по величине уже порядка
корня из n, а значит имеют в два раза меньшую битовую длину. Отметим также,
что применение вычислений согласно китайской теореме об остатках делает
алгоритм RSA восприимчивым к атакам по времени.
. На теореме
основаны схема Асмута — Блума и схема Миньотта — пороговые схемы разделения
секрета в группе участников. Секрет могут узнать только k из n участников, объединив
свои ключи.
. Одним из
применения является быстрое преобразование Фурье на основе простых чисел
. Теорема лежит в
основе принципа Хассе поиска целочисленных корней уравнения.
. Из теоремы
следует мультипликативность функции Эйлера.
. На теореме
основывается алгоритм Полига-Хеллмана нахождения дискретного логарифма за
полиномиальное время для чисел, имеющих специальный вид.
. Теорема имеет
множество применений в шифровании и дешифровании в криптографических системах,
например, в криптосистеме Рабина или в шифре Виженера.
Глава 1. Элементарная
теория сравнений, а ≡ b (mod p)
. Определения и
основные свойства сравнений
В данном параграфе мы
рассмотрим целые числа, а обозначать их будем латинскими буквами.
Возьмём произвольное
фиксированное натуральное число p и будем рассматривать остатки при делении на
р различных целых чисел.
При рассмотрении свойств
этих остатков и проведении операций над ними удобно ввести понятие сравнения по
модулю.
Определение. Целые числа а и b называются сравнимыми по модулю р, если разность чисел а — b делится на р, то есть,
если . Таким образом
сравнение представляет собой соотношение между тремя числами a,b и p, причем p,играющее своего рода
эталона сравнения, мы называем модулем. Для краткости мы будем это соотношение
между a, b и p записывать следующим образом: a≡b (mod p), a и b будем называть соответственно левой и правой частями сравнения.
Число p, стоящее под знаком
модуля, будем всегда считать положительным, т.е запись mod p будет означать, что, числа а и b — вычеты. Если разность а
— b не делится на р, то а не
сравнимо с b по mod p.
Согласно определению а ≡ 0
(mod p) означает, что а делится
на р.
Пример:
≡ 17 (mod 21)т. к. 101 — 17 = 84, а
84⁞21.
Теорема: число а сравнимо с числом b по модулю p тогда и только тогда, когда а и b имеют одинаковые остатки при делении на р, поэтому в качестве
определения сравнения можно взять следующее:
Определение: Целые числа а и b называются сравнимыми по модулю р, если остатки от деления этих
чисел на р равны.
Дадим основные свойства
сравнений:
. Рефлексивность
отношения сравнимости: а ≡ a (mod p)
.Симметричность отношения
сравнимости:
если, а ≡ b (mod p) то b ≡ a (mod p).
3. Транзитивность отношения
сравнимости:
если а ≡ b (mod p), b ≡ c (mod p), то а ≡ c(mod p).
. Если а ≡ b (mod p) и k — произвольное целое
число, то kа ≡ kb (mod p)
. Если kа ≡ kb (mod p) и (k, p) = 1, то а ≡ b (mod p).
. Если а ≡ b (mod p)и k— произвольное натуральное
число, то kа ≡ kb (mod kp)
. Если kа ≡ kb (mod kp), где k и р — произвольные
натуральные числа, то а ≡ b (mod p)
. Если а ≡ b (mod p),c ≡ d (mod p), то а+c ≡ b+d (mod p)и а-c ≡ b—d (mod p).
. Если а ≡ b (mod p), c ≡ d (mod p), то аc ≡ bd (mod p)
. Если а ≡ b (mod p), то при любом целом n > 0,а ≡ b (mod p).
. Если а ≡ b (mod p) и f(x)= +
+
+… — произвольный многочлен с целыми
коэффициентами, то f(а) ≡ f(b) (mod p)
. Любое слагаемое
левой или правой части сравнения можно перенести с противоположным знаком в другую
часть.
. Если а ≡ b (mod p) и , то а ≡ b (mod d)
. Если а ≡ b (mod p), то множество общих
делителей а и р совпадает с множеством общих делителей b и р. В частности, (a,p)=(b,p).
. Если а ≡ b (mod ),а ≡ b (mod
)…,а ≡ b (mod
), то а ≡ b (mod p), где p=[
,
,…,
].
При делении целого числа
на модуль р в остатке получается 0, 1, 2, 3,…,р- 1 чисел.
2. Теорема Эйлера,
теорема Ферма
элементарный теорема китайский остаток
Теорема (Эйлера). Пусть m>1,(a,m)=1,j(m)- функция Эйлера. Тогда: aj(m)≡1(mod m)
Доказательство. Пусть х пробегает приведенную систему вычетов по mod m:
x=,
,…,rc
где c=j(m) их число ,…,
— наименьшие неотрицательные
вычеты по mod m. Следовательно,
наименьшие неотрицательные вычеты, соответствующие числам ax суть соответственно: — тоже пробегают приведенную
систему вычетов, но в другом порядке. Значит:
a≡
(mod m) a
≡
(mod m) … arc≡
(mod m), c=φ(m)
Перемножим эти с штук
сравнений. Получится:
≡
(mod m)
Так как ≠0 и взаимно просто с модулем m, то, поделив последнее
сравнение на r1r2…rc, получим ).
Теорема (Ферма). Пусть р — простое число, р не делит a. Тогда: a p-1≡1(mod p).
Доказательство 1. Положим в условии теоремы Эйлера m=p, тогда φ (m)=p-1. Получаем.
Замечание: Необходимо отметить важность условия взаимной простоты модуля и
числа a в формулировках теорем
Эйлера и Ферма. Простой пример: сравнение очевидно не выполняется.
Однако можно легко
подправить формулировку теоремы Ферма, чтобы снять ограничение взаимной
простоты.
Глава 2. Китайская
теорема об остатках
. Китайская теорема
об остатках
Одним из важных
результатов теории чисел является так называемая китайская теорема об остатках
(KTO). По существу эта теорема утверждает, что можно восстановить целое число
по множеству его остатков от деления на числа из некоторого набора попарно
взаимно простых чисел. Эта теорема в её арифметической формулировке была
описана в трактате китайского математика Сунь Цзы «Сунь Цзы Суань Цзин»
(кит.упр.孙子算经, пиньинь: sunzi suanjing), предположительно датируемом третьим
веком н. э. и затем была обобщена Цинь Цзюшао в его книге «Математические
рассуждения в 9 главах» датируемой 1247 годом, где было приведено точное
решение.Существует несколько формулировок данной теоремы, я предоставлю здесь
некоторые из них.
Теорема. Пусть , 1 ≤ i ≤ k, взаимно простые числа
и пусть ai целые числа. Тогда
существует такое число x,
что имеет место
x≡ mod
,
x≡ ,
…
x≡ .
Наконец, рассмотрим еще
одну формулировку теоремы,
которую будем использовать
в практических работах.
Теорема. Пусть {} —
взаимно простые числа и M =
Пусть 0 ≤ ≤
, целые числа. Введем обозначение
=
. Пусть
число, которое удовлетворяет сравнению
≡1 mod
.При этих условиях сравнение
x≡ mod
, имеет на интервале [0, M — 1] единственное
решение,которое определяется формулой x = +
+ … +
В рамках условий теоремы
китайская теорема об остатках утверждает, что существует взаимно однозначное
соответствие между целыми числами и некоторым наборами целых чисел. Другими
словами, для каждого целого числа B найдется соответствующий ему единственный набор чисел и наоборот, для каждого набора
чисел () найдется
единственное соответствующему этому набору число B.
Арифметическая
формулировка КТО:
Если числа попарно
взаимно просты, то для любых остатков таких, что при всех i=
1,2,…n., найдётся число N,
которое при делении на даёт остаток при всех i= 1,2,…n.
Доказательство:
Применим индукцию
по n. При n=1 утверждение теоремы очевидно. Пусть теорема справедлива при n= k-1, т. е. существует число M,
дающее остаток при делении на при .Обозначим и рассмотрим числа . Покажем, что
хотя бы одно из этих чисел даёт остаток при делении на . Допустим это не так.
Поскольку количество чисел равно , а возможных остатков при делении этих чисел
на может быть не более чем (ведь ни одно число не даёт остаток ), то среди них
найдутся два числа, имеющих равные остатки (принцип Дирихле). Пусть это числа
и при и . Тогда их разность делится на , что невозможно, т.к. и взаимно просто с , ибо числа попарно взаимно просты (по условию).
Противоречие.
Таким образом,
среди рассматриваемых чисел найдётся число , которое при делении на даёт
остаток . В то же время при делении на число N даёт остатки соответственно.
Наиболее
используемая формулировка КТО:
Пусть — попарно взаимно простые
числа и — произвольные целые числа. Тогда существует целое число ,такое что
Целое число у удовлетворяет условию
тогда и только тогда когда
Доказательство: Обозначим М=и
. Тогда числа
являются взаимно простыми для
всех i. Cледовательно существует целое число такое что
где
. Положим
тогда
, поскольку числа
. Аналогично доказывается, что
. Пусть
— остаток от деления числа a на M. Тогда
и
≡ a (mod M). В частности
Далее, пусть целое чисто у удовлетворяет условию
. Тогда
т. е. Число
делится на каждое из чисел
.В силу того, что числа
попарно взаимно простые, получаем что
делится на число
. Таким образом,
≡0 (mod
).Теорема
доказана.
2. Примеры.
Применение к решению олимпиадных задач
В этом параграфе я опишу
один из методов решения систем линейных сравнений. Это очень древний алгоритм.
Он применялся еще в античности для решения проблем астрономии. Приведу
несколько примеров решения олимпиадных задач и примеров решения сравнений с
помощью КТО. Начнем с задачи, сформулированной на современном языке, которая могла
бы рассматриваться древними астрономами (Астрономический пример).
Пример 1: Три спутника пересекут меридиан города Лидса сегодня ночью:
первый — в 1 ночи, второй — в 4 утра, а третий — в 8 утра. У каждого спутника
свой период обращения. Первому на полный оборот вокруг Земли требуется 13
часов, второму — 15, а третьему — 19 часов. Сколько часов пройдет (от полуночи)
до того момента, когда спутники одновременно пересекут меридиан Лидса?
Посмотрим, как эта задача
переводится на язык сравнений.
Пусть х — количество
часов, которые пройдут с 12 часов ночи до момента одновременного прохождения
спутниками над меридианом Лидса. Первый спутник пересекает этот меридиан каждые
13 часов, начиная с часу ночи. Это можно записать
как х = 1 + 13t для некоторого целого t. Другими словами, х ≡ 1 (mod 13). Соответствующие
уравнения для остальных спутников имеют вид: х ≡ 4 (mod 15) и х≡ 8 (mod 19). Таким образом, три
спутника одновременно пересекут меридиан Лидса через х часов, если х
удовлетворяет эти трем уравнениям. Следовательно, для ответа на поставленный
вопрос достаточно решить систему сравнений:
х ≡ 1 (mod 13),
х ≡4 (mod 15), (B1)
х ≡ 8 (mod 19).
Заметим, что мы не можем
складывать или вычитать уравнения системы, поскольку модули сравнений в них
разные. Будем решать эту задачу, переходя от сравнений к уравнениям в целых
числах. Так, сравнение х ≡ 1 (mod 13) соответствует диофантову уравнению: х = 1 + 13t. Заменяя х во втором
сравнении системы на 1 + 13t, получаем:
+ 13t ≡ 4 (mod 15), т.е. 13t ≡ 3 (mod 15).
Но 13 обратимо по модулю
15, обратный к нему элемент — это 7. Умножая последнее сравнение на 7 и
переходя в нем к вычетам по модулю 15, имеем:
t ≡ 6 (mod 15).
Значит, t может быть записан в
виде: t = 6+15u для какого-то целого u. Следовательно,
х = 1 + 13t = 1 + 13(6 + 15u) = 79 + 195u.Заметим, что все числа
вида 79 + 195u являются целыми решениями первых двух сравнений системы (B.1). Наконец, подставим в
третье сравнение вместо х выражение 79 + 195u:
+ 195u ≡ 8 (mod 19), так что 5u ≡ 5 (mod 19).
Ввиду обратимости остатка
5 по модулю 19, на него можно сократить и увидеть, что
u ≡ 1 (mod 19). Переписывая это сравнение как диофантово уравнение, мы
получим
u= 1 + 19v для некоторого целого v.
Итак, х = 79 + 195u = 79 + 195(1 + 19v) = 274 + 3705v.
Какой отсюда можно сделать
вывод относительно спутников? Напомним, что х — количество часов, которые
пройдут от полуночи до момента одновременного прохождения спутников над
меридианом Лидса. Поэтому нам нужно было найти наименьшее натуральное значение
переменной х, удовлетворяющее системе (B.1). Мы это сделали. Поскольку решение системы: х = 274 + 3705v, то ответ: 274. Итак,
спутники одновременно пройдут над меридианом Лидса через 274 часа после 0 часов
сегодняшней ночи, что соответствует 11 дням и 10 часам. Но общее решение
системы дает больше информации. Прибавляя к 274 любое кратное 3705, мы получаем
другое решение системы. Иначе говоря, спутники одновременно пересекают
означенный меридиан каждые 3705 часов после первого такого момента, что
соответствует 154 дням и 9 часам.
Пример 2: Найти все целые решения системы сравнений:
Решение: М= 3*5*7=105
Найдем целые числа ,
,
такие что :
1)*35≡1 (mod 3)
*2≡1 (mod 3)
=-1(mod 3)
)*21≡1 (mod 5)
*1≡1 (mod 5)
=1
)*15≡1 (mod 7)
=1
По КТО:
≡
,
подставим найденные нами
значения в формулу:
≡-1*35*2+
1*21*3+1*15*2=23, т. е.
Числа вида 23+105t, где ,исчерпывают все множество решений
исходной системы сравнений.
Ответ: 23+105t.
Пример 3: Доказать что сравнение ≡ 0 (mod m)разрешимо для каждого натурально числа m>1, несмотря на то, что
уравнение =0 не имеет
целых решений.
Поскольку =(2x+1)(3x+1), то уравнение
не имеет решений в кольце
. Пусть m=
(2b+1). тогда по китайской
теореме об остатках существует целое число х, такое, что 3х≡ -1(mod) и 2х≡-1(mod(2b+1)). Следовательно
≡0 (mod m).
Пример 4: Доказать что в каждой возрастающей арифметической прогрессии,
состоящей из натуральных чисел, существует отрезок произвольной длины,
состоящий только из составных чисел.
Рассмотрим арифметическую
прогрессию b,b+a,b+2a,…, где a,bN, Пусть
,
,…,
— простые числа, причем a<
<
<…<
. По Китайской теореме об остатках существует
натуральное число,
такое,что a≡-b—aj (mod
), где j=1,2,…,m. Это означает, что числа b+a(
+1), b+a(
+2), b+a(
+m) являются составными.
Пример 5: Доказать что для любых натуральных чисел ,таких что
)=
)=…=(
=1, уравнение
имеет бесконечно много натуральных решений. Если
n=1,то ,
— решение уравнения
=
при любом z
.Если n>2, то по китайской теореме об остатках существует бесконечно
много таких чисел z, что z
(mod
), z
(mod
). Для каждого
такого z числа
,
…,
,
являются решениями нашего
уравнения.
3. КТО. Применение к
открытию сейфа в банке
Бенджамен Франклин (Franklin) однажды сказал:
«Трое могут хранить тайну, если двое из них мертвы». В этом параграфе мы
изучаем безопасную систему допуска живых к секретным сведениям, основанную на
китайской теореме об остатках. Представьте себе следующую ситуацию
Пусть -попарно взаимно простые числа, такие,
что .Пусть S— произвольное целое число
с условием M<S<N и — остатки
от деления S на .
Предположим, далее, что в
некотором банке работают n кассиров. Кассир с номером i знает пару чисел .Для открытия сейфа необходимо знать ключевое
число S. Докажем, что любые k кассиров смогут открыть
сейф, но никакие (k-1) кассиров не смогут это сделать. Действительно, пусть собрались
кассиры с номерами ,
тогда им известен набор чисел По КТО можно найти такое число
, что
. Так как
, то a=S (ввиду единственности решения этой системы сравнений по модулю
) и ключевое число найдено,
т.е. сейф можно открыть. Если собрались (k-1) кассиров, то они знают пары чисел. По КТО они могут найти
такое целое число b, что и
, т. е. b≠S. Таким образом, b не является искомым
ключом к открытию сейфа.
В качестве конкретного
примера можно рассмотреть числа : и,например, S=4001. Каждый из пяти кассиров знает одну из пар чисел (5,9),
(1.10), (32,49), (32,53),(48,59).
Из предыдущего следует,
что любые три кассира смогут найти ключ (равный S=4001) и открыть сейф, но никакие два не смогут этого сделать.
Заключение
В выше приведённой работе
была сформулирована китайская теорема об остатках, приведены её доказательства,
а также указанно применение КТО к решению олимпиадных задач и к некоторым
прикладным вопросам теории чисел.
Список литературы
1. Бухштаб А.А. Теория чисел. — М: Просвящение,1996.
. Кузьмина А.С., Мальцев Ю.А. Теория чисел: учебное
пособие/ А.С. Кузьмина, Ю.Н. Мальцев. — Барнаул: АлтГПА,2011.-240с.
. Коутинхо С. Введение в теорию чисел. Алгоритм RSA. Москва: Постчаркет,
2001. — 328 с.
. Рыбников К.А. История математики: учебное пособие для
университетов-Издательство Московского Университета,1960.
Массачусетский Технологический институт. Курс лекций #6.858. «Безопасность компьютерных систем». Николай Зельдович, Джеймс Микенс. 2014 год
Computer Systems Security — это курс о разработке и внедрении защищенных компьютерных систем. Лекции охватывают модели угроз, атаки, которые ставят под угрозу безопасность, и методы обеспечения безопасности на основе последних научных работ. Темы включают в себя безопасность операционной системы (ОС), возможности, управление потоками информации, языковую безопасность, сетевые протоколы, аппаратную защиту и безопасность в веб-приложениях.
Лекция 1: «Вступление: модели угроз» Часть 1 / Часть 2 / Часть 3
Лекция 2: «Контроль хакерских атак» Часть 1 / Часть 2 / Часть 3
Лекция 3: «Переполнение буфера: эксплойты и защита» Часть 1 / Часть 2 / Часть 3
Лекция 4: «Разделение привилегий» Часть 1 / Часть 2 / Часть 3
Лекция 5: «Откуда берутся ошибки систем безопасности» Часть 1 / Часть 2
Лекция 6: «Возможности» Часть 1 / Часть 2 / Часть 3
Лекция 7: «Песочница Native Client» Часть 1 / Часть 2 / Часть 3
Лекция 8: «Модель сетевой безопасности» Часть 1 / Часть 2 / Часть 3
Лекция 9: «Безопасность Web-приложений» Часть 1 / Часть 2 / Часть 3
Лекция 10: «Символьное выполнение» Часть 1 / Часть 2 / Часть 3
Лекция 11: «Язык программирования Ur/Web» Часть 1 / Часть 2 / Часть 3
Лекция 12: «Сетевая безопасность» Часть 1 / Часть 2 / Часть 3
Лекция 13: «Сетевые протоколы» Часть 1 / Часть 2 / Часть 3
Лекция 14: «SSL и HTTPS» Часть 1 / Часть 2 / Часть 3
Лекция 15: «Медицинское программное обеспечение» Часть 1 / Часть 2 / Часть 3
Лекция 16: «Атаки через побочный канал» Часть 1 / Часть 2 / Часть 3
Ладно, ребята, давайте начнем. Итак, сегодня мы поговорим об атаках через побочные каналы, общей проблеме, свойственной всем видам систем. В широком смысле атаки через побочный канал возникают в ситуации, когда вы не думаете, что какая-то информация способна раскрыть сведения о вашей системе.
Как правило, у вас есть несколько компонентов, которые устанавливают связь между пользователем и сервером. При этом вы думаете, что знаете обо всём, что проходит по этому проводу, связывающему двух абонентов, знаете обо всех битах, которыми пользователь и сервер обмениваются друг с другом, и это безопасно. Но часто бывает так, что некая информация всё же раскрывается пользователем или сервером. Пример, о котором говорится в материалах сегодняшней лекции, описывает ситуацию, когда синхронизация сообщений между пользователем и сервером раскрывает некоторую дополнительную информацию, о которой вы бы не узнали, просто наблюдая за потоком битов между этими абонентами.
На самом деле, есть гораздо более широкий класс побочных каналов, относительно которых вы можете беспокоиться. О появлении побочных каналов люди узнали ещё в 40-х годах, когда обнаружили, что если вы начинаете печатать символы на телетайпе, то электроника телетайпа начнёт излучать радиочастотную радиацию. При этом можно просто расположить рядом осциллограф и наблюдать, как изменяется частота радиосигнала в зависимости от того, какой символ печатает оператор телетайпа. Таким образом, радиочастотное излучение является классическим примером побочного канала, который заставляет вас беспокоиться.
Есть много других примеров, замеченных людьми, таких, как потребление электроэнергии. Это еще один побочный канал, о котором вы можете беспокоиться, так как ваш компьютер будет использовать разное количество энергии в зависимости от того, что именно он вычисляет.
Примером побочного канала может служить звук, благодаря которому также возможны утечки информации. Например, люди слушают принтер и, основываясь на издаваемых им звуках, могут сказать, какие символы он печатает. Это особенно легко сделать для матричных принтеров с точечной печатью, которые во время печати издают очень надоедливые звуки.
И вообще, это то, о чём стоить подумать. На лекции в понедельник Кевин также упомянул некоторые интересные побочные каналы, которыми он занимается в своих исследованиях. Но мы собираемся рассмотреть конкретный побочный канал, который изучали Дэвид Брамли и Дэн Бонэ. В своей работе, опубликованной около 10 лет назад, они пишут, что смогли извлечь криптографический ключ веб-сервера Apache путем измерения тайминга разных ответов на различные входные пакеты враждебного клиента. В данном конкретном случае они «охотились» за криптографическим ключом. В действительности, многие атаки через побочный канал нацелены на криптографические ключи отчасти потому, что довольно сложно получить большое количество данных через такой канал. А криптографические ключи — это одна из ситуаций, когда на выходе получается небольшое количество бит, то есть во время атаки злоумышленники могут извлечь около 200 — 256 бит информации. Но основываясь только на этих 200 битах, они способны взломать криптографический ключ этого веб-сервера.
Если же вы пытаетесь просочиться в какую-то базу данных, полную номеров социального страхования, вам потребуется «слить» из неё очень много бит информации. Вот почему большинство атак через побочные каналы сосредотачиваются на получении небольших секретов, таких как криптографические ключи или пароли. Но в целом это применимо и ко многим другим ситуациям.
В материалах лекции описана ещё одна классная вещь — это то, что всё это можно проделать по сети. Вероятно, вы поняли, что им пришлось проделать много тщательной работы, чтобы уловить эти мельчайшие различия во временной информации. Каждый запрос, который они отправляли на сервер, отличался от другого запроса на 1-2 микросекунды, что является очень малым промежутком времени. Поэтому вы должны быть очень осторожны, так как наши сети не позволяют уловить такую временную разницу и определить, что сервер обрабатывал ваш запрос на 1-2 микросекунды дольше, чем был должен.
В результате было не ясно, можно ли организовать подобную атаку в очень «зашумленной» сети, так как полезная информация должна быть отделена от уровня шумов. Эти ребята были одними из первых, кто показал, что вы действительно можете проделать подобное по сети Ethernet с сервером на одном конце сети и клиентом на другом конце. Они доказали, что действительно можно измерить эти различия частично путем усреднения, частично с помощью других трюков.
План остальной части этой лекции таков – сначала мы погрузимся в детали криптографического алгоритма с открытым ключом RSA, который использовали эти ребята. Мы не будем оценивать его с точки зрения безопасности, а будем смотреть, как это реализуется, потому что именно реализация алгоритма является критичной для использования побочного канала.
Брамли и Бонэ тщательно исследовали различные детали реализации, чтобы понять, в каких случаях некоторые вещи выполнялись быстрее или медленнее. Так что сначала мы должны узнать, как реализуется криптосистема RSA, а затем вернемся и выясним, как можно атаковать все эти структуры, имеющиеся в RSA.
Давайте начнем с рассмотрения RSA на высоком уровне. RSA – это довольно широко используемая криптосистема с открытым ключом. Мы упоминали этих парней пару недель назад, когда говорили о сертификатах. Теперь мы собираемся посмотреть, как это работает на самом деле.
Как правило, есть 3 вещи, о которых вам нужно побеспокоиться – это генерирование ключа, шифрование и расшифровка. В RSA способ создания ключа заключается в выборе 2 больших простых целых чисел, обозначим их p и q. В своей статье эти ребята пишут о p и q каждое размером по 512 бит. Обычно это называется 1024 битным RSA, потому что произведение этих простых чисел — это 1000-битное целое число. В наши дни, это, вероятно, не слишком хороший выбор для размера ключа RSA, потому что его взлом – относительно легкая задача для злоумышленников. Так что если 10 лет назад 1000 бит казались разумной величиной, сегодня при построении системы следует выбрать 2000, 3000 или даже 4000 битный ключ RSA. Так что размер ключа RSA означает размер этих простых чисел.
Затем, для удобства, мы поговорим о числе n, которое является просто произведением этих простых чисел n=pq, и это число называется модулем. Итак, теперь, когда мы знаем, как создать ключ, или, по крайней мере, часть ключа, нам придется выяснить, как зашифровывать и расшифровывать сообщения.
И то, как мы будем шифровать и расшифровывать сообщения, основано на возведении в степень чисел по модулю n. Это кажется немного странным, но мы разберёмся с этим через секунду. Так что если вы хотите зашифровать сообщение m, вы должны преобразовать его в me по mod n. Величина e – это степень, через секунду мы выясним, как её выбирать. Вот таким образом мы собираемся зашифровать сообщение.
То есть мы просто возьмем это сообщение как целое число и возведем его в степень. Через секунду мы посмотрим, почему это работает, а пока что обозначим всё это зашифрованное сообщение литерой С.
Затем, чтобы расшифровать его, мы должны найти другую интересную экспоненту d, которая позволяет взять зашифрованное сообщение C, возвести его в степень d по модулю n и в результате волшебным образом получить расшифрованное сообщение m.
Итак, общий принцип заключается в использовании одной экспоненты для шифрования сообщения и другой экспоненты для его расшифровки.
В целом, кажется, немного трудно понять, как мы собираемся придумать эти два магических числа, которые каким-то образом возвращают нам первоначальное сообщение. Но если вы посмотрите, как работает возведение в степень или умножение по модулю этого числа n, то всё поймёте.
Если взять Х и возвести его в степень, равную функции φ от n, то это будет равно 1 по модулю n:
X φ(n) = 1 mod n
Эта функция «фи» для нашего конкретного выбора n довольно проста, она равна φ = (p-1)(q-1).
Тогда произведение открытой экспоненты е, которое больше 1, но меньше φ(n), на секретную экспоненту d, будет равно:
ed = ɑφ(n) +1, где ɑ — некая константа.
Таким образом, удаётся правильно расшифровать сообщение, так как существует достаточно простой алгоритм, если вы знаете значение φ(n) для того, чтобы вычислить d с учетом e или e с учетом d.
Аудитория: разве 1 по модулю n не равна 1?
Профессор: да, я здесь допустил неточность, равенство должно выглядеть так:
X φ(n) mod n = 1 mod n, то есть величина Х в степени функции «фи» от n по модулю n равна единице по модулю n.
В основном это означает, что для RSA мы должны выбрать некоторое значение е, которое будет нашим значением шифрования. Затем из e мы собираемся сгенерировать d на основе формулы d.e = 1 mod φ(n), отсюда d = 1/e mod φ(n).
Есть некоторые Эвклидовы алгоритмы, которые вы можете эффективно использовать для этого вычисления. Но для того, чтобы сделать это, вы должны знать эту φ(n), которая требует факторизации, то есть разложения нашего числа n на множители p и q.
Итак, RSA является системой, где открытый ключ — это пара: экспонента шифрования е и число n, а пара d и n – это закрытый ключ, который держится в секрете. Так что любой может возвести сообщение в степень, чтобы зашифровать его для вас. Но только вы знаете это значение d и поэтому сможете расшифровать сообщение. И до тех пор, пока вы не знаете факторизацию этих множителей P и Q, или N, равное произведению P и Q, вы не знаете, что собой представляет φ = (p-1)(q-1).
В результате вычислить это значение d — достаточно трудная задача. Вот что в общих чертах представляет собой алгоритм RSA на высоком уровне.
Теперь, когда мы ознакомились с принципами RSA, я хочу остановиться на 2-х вещах. Есть хитрости, как правильно его использовать и есть подводные камни, возникающие при его использовании. Существуют множество способов, как реализовать код для этого возведения в степень и делать это эффективно. Это довольно незаурядная задача, потому мы имеем дело 1000-битными целыми числами, для которых нельзя просто выполнить инструкцию умножения. Вероятно, потребуется много времени, чтобы сделать эти операции.
Поэтому первое, что я хочу упомянуть, — это различные подводные камни RSA. Один из них — это мультипликативность. Предположим, у нас есть 2 сообщения: m0 и m1. Я зашифрую их, превратив m0 в m0e mod n, а m1 в m1e mod n. Возможной проблемой, вернее, не обязательно проблемой, но неприятным сюрпризом для того, кто использует RSA, будет то, что очень легко произвести шифрование произведения m0 на m1, потому что вы просто умножаете эти 2 цифры: m0e mod n * m1e mod n.
Если вы их умножите, то в результате получите произведение (m0m1)e по модулю n. Это корректное шифрование при упрощенном использовании RSA для значения m0m1. На данный момент это не большая проблема, потому что вы просто можете создать это зашифрованное сообщение, но не в состоянии его расшифровать. Однако существует возможность, что общая система позволит вам расшифровать определенные сообщения. То есть если она позволяет вам расшифровать созданное вами сообщение, то возможно, следуя обратным путём, вы сможете узнать, что собой представляют эти сообщения m0 и m1.
Данный факт не стоит игнорировать, так как он влияет на ряд протоколов, использующих RSA. Существует одно свойство, которым мы воспользуемся в качестве защитного механизма в конце нашей лекции.
Второй подводный камень, или свойство RSA, на которое стоит обратить внимание – это детерминированность, или определяемость. В описанной ранее элементарной реализации, если вы берете сообщение m и шифруете его, превращая в me mod n, то это детерминированная функция сообщения. Поэтому, если вы зашифруете его снова, вы получите точно такое же шифрование.
Это не желательное свойство, потому что, если я вижу, что вы посылаете какое-то сообщение, зашифрованное с помощью RSA, и хочу знать, что это такое, мне может быть трудно его расшифровать. Но я могу попробовать разные вещи, в результате которых я вижу, что вы посылаете это сообщение.
Тогда я зашифрую его и посмотрю, получите ли вы тот же зашифрованный текст. И если это так, то я узнаю, что вы зашифровали. Потому что все, что мне нужно для шифрования сообщения — это общедоступный открытый ключ, который представляет собой пару чисел (n,e).
Так что это не так уж и здорово, и вам, возможно, придётся быть внимательным с этим свойством при использовании RSA. Таким образом, примитивы такого рода достаточно трудно непосредственно использовать.
На практике, чтобы избежать подобных проблем с RSA, люди перед шифрованием кодируют сообщение определенным образом. Вместо того, чтобы напрямую возводить в степень сообщение, они берут какую-то функцию сообщения и возводят её в степень по модулю n:
(f(m))e mod n.
Эта функция f, обычно используемая в наши дни, называется OAEP — Оптимальным Ассиметричным Шифрованием с Дополнением. Это нечто закодированное, обладающее двумя интересными свойствами.
Во-первых, оно привносит случайность. Вы можете думать о f(m) как о генерации 1000-битного сообщения, которое вы собираетесь зашифровать. Частью этого сообщения будет ваше сообщение m здесь, в середине этого прямоугольника. Конечно, вы сможете получить его обратно при расшифровке. Итак, есть 2 интересные вещи, которые вы хотите сделать: справа вы размещаете некую случайность, значение r. Оно даёт то, что если вы зашифруете сообщение несколько раз, то каждый раз будете получать разные результаты, так что шифрование больше не будет детерминировано.
Для того, чтобы превозмочь это мультипликативное свойство и другие виды проблем, слева вы располагаете некое дополнение pad, которое представляет собой последовательность типа 1 0 1 0 1 0. Можно выбрать последовательность и получше, но грубо говоря, это какая-то предсказуемая последовательность, которую вы вставляете сюда и всякий раз, когда вы расшифровываете сообщение, вы убеждаетесь, что эта последовательность все еще там. Мультипликативность уничтожит эти биты pad, и тогда вам будет ясно, что кто-то испортил ваше сообщение и отбросил его. Если же эти биты остаются на месте, это доказывает, что никто не подделал ваше сообщение и вы в состоянии принять его, так как оно было правильно кем-то зашифровано.
Аудитория: если злоумышленник знает, насколько велико значение pad, не может ли он установить 1 в самый низ последовательности, а затем мультиплицировать это значение?
Профессор: да, возможно. Это немного сложно, потому что эта случайность r будет распространяться далее. Так что конкретная конструкция этого OAEP немного сложнее того, что я изобразил. Но представьте, что это целочисленное, а не битовое умножение, случайность распространяется далее, поэтому вы сможете создать такую схему OAEP, в которой подобное не будет происходить.
Получается, что вы не должны использовать эту математику RSA напрямую, на практике вы должны использовать некую библиотеку, которая реализует для вас все эти вещи правильным образом, и применять её как параметр шифрования и дешифрования.
Однако рассмотренные выше детали будут иметь для нас значение, так как мы на самом деле пытаемся выяснить, как сломать или как атаковать существующую реализацию RSA.
В частности, атака, описанная в лекционной статье, будет использовать тот факт, что сервер собирается проверить это дополнение pading, когда он получит сообщение. Так вот как мы собираемся рассмотреть время, которое потребуется серверу для расшифровки. Мы собираемся отправить тщательно построенное сообщение, но оно не создано из реального сообщения m и его шифрования. Мы собираемся создать тщательное зашифрованное целочисленное значение.
Сервер попытается его расшифровать и получит некую несуразность, с которой с высокой долей вероятности не будет сопрягаться дополнение pad, и сервер сразу же отклонит это сообщение. Это именно то, что нам требуется, потому что таким образом сервер точно скажет нам, сколько времени ему потребовалось, чтобы добраться до этой точки: расшифровать RSA, получить это сообщение, проверить дополнение и отклонить его. Вот что мы будем измерять в этой атаке, описанной в лекционном материале. В этом сообщении имеется некий целостный компонент, который позволит нам определить время дешифровки.
Итак, теперь давайте поговорим о том, как нам реализовать RSA. Суть реализации заключается в возведении в степень, что довольно нетривиально, как я упоминал ранее, потому что все это очень большие целые числа. Само сообщение, по крайней мере, в этой статье, представляет собой 1000 разрядное целое число. И сама экспонента e также будет иметь довольно большое значение.
По крайней мере, экспонента шифрования хорошо известна. Но лучше, чтобы экспонента расшифровки была большим числом также порядка 1000 бит. Так что у вас есть 1000-битное целое число, которое вы хотите возвести в 1000 битную целую степень по модулю ещё одного 1000 битного целого числа n, что будет довольно трудоёмко. Поэтому практически в каждой реализации RSA предусмотрена оптимизация, позволяющая сделать этот процесс немного быстрее.
Есть 4 основных оптимизации, которые имеют значение для этой атаки. На самом деле их больше, но самыми важными являются следующие. Первая называется китайской теоремой об остатках, или CRT. Просто вспомните её из курса средней или высшей школы. Она утверждает следующее. Предположим, что у вас есть два числа, у вас имеется некоторое значение Х, и вы знаете, что [Х = a1] mod p и одновременно [Х = a2] mod q, где р и q – простые числа, и это модульное равенство применимо ко всему уравнению.
Выясняется, что у этой системы уравнений есть уникальное решение [Х = Х1] mod pq. Существует такая уникальная величина Х1, которую на самом деле можно очень эффективно вычислить. Китайская теорема об остатках снабжена алгоритмом вычисления этого уникального простого числа Х1, которое равно Х mod pq при значениях соответственно a1 и a2 mod p и q.
Хорошо, так как можно использовать эту китайскую теорему об остатках для ускорения модульного возведение в степень? Нам поможет то, что если вы заметили, мы делаем вычисление некоторой связки вещей по модулю n, который равен p умноженному на q.
Китайская теорема об остатках говорит, что если вы хотите узнать значение mod pq, достаточно вычислить значение mod p и значение mod q. После этого китайская теорема об остатках используется для того, чтобы найти единственно верное решение того, что такое mod pq. Как вы думаете, почему это быстрее? Ведь похоже, что вы делаете одно и то же дважды, а это больше работы по рекомбинации?
Аудитория: вероятно, эти значения достаточны малы и позволяют провести вычисление быстрее?
Профессор: ну, они конечно меньше, но не настолько, чтобы это оказало существенное влияние. Итак, произведение p и q, или число n составляет около 1000 бит, p и q оба по 500 бит, но они всё ещё не похожи на размер машинного слова. Но это нам поможет, потому что большая часть того, что мы делаем в этих вычислениях — это умножение, и оно примерно равно квадрату тех вещей, которые вы умножаете. Вспомните метод умножения из курса высшей школы — вы берете все цифры одного числа и умножаете их на все остальные цифры в другом числе. Как следствие, умножение, возведение в степень на выходе выдаёт примерно квадратичный размер исходного числа. Так что если мы по существу идем от 1000 битов до 512 битов, то мы уменьшаем размер входных данных в 2 раза. Это означает, что все возведение в степень будет примерно в 4 раза проще. Так что если мы просчитаем эти выражения [Х = a1] mod p и [Х = a2] mod q дважды, мы ускорим процесс вычисления в 4 раза. Так что в итоге применение китайской теоремы об остатках даёт повышение производительности в 2 раза при выполнении любой операции RSA как при шифровании, так и при дешифровке.
Это первая оптимизация, которую использует большинство людей.
Вторая оптимизация основана на технике, которая носит название Sliding windows, «скользящие окна». Мы рассмотрим два этапа этой оптимизации. Сначала рассмотрим, с помощью каких основных операций выполняется это возведение в степень.
Предположим, у вас есть какой-то зашифрованный текст С, который теперь составляет 500 бит, потому что вы не делали mod p или mod q, и примерно такого же размера d. Так как же возвести c в степень d? Я думаю, что глупо просто взять c и перемножить её саму на себя d раз. Но экспонента d очень большая, около 500, так что это никогда не закончится. Более эффективный план состоит в том, чтобы сделать то, что называется повторением квадрирования. Это шаг, который нужно совершить перед «скользящими окнами». Технически повторение квадрирования выглядит так.
Если вы хотите вычислить c2x, то вы можете вычислить С в степени Х и затем возвести его в квадрат: (cx)2:
c2x = (cx)2
В нашем простом плане вычисление c2x потребовало бы от нас в два раза больше итераций умножения, потому что С умножается 2 раза, но гораздо умнее будет сначала вычислить cx, а позже возвести эту величину в квадрат. Так как это работает довольно хорошо, то мы можем использовать этот принцип и для другой экспоненты, например c2x+1:
c2x+1 = (cx)2 x с
Это и называется повторением квадрирования.
Этот приём позволяет нам вычислить эти степени, или модульные степени, во время, линейное в размере экспоненты. Таким образом, каждый бит экспоненты мы либо возводим в квадрат, либо возводим в квадрат, а затем умножаем. Таков план повторения квадрирования, позволяющий не тратить много времени на вычисление модульных экспонент.
В чём же заключается трюк со «скользящими окнами», о которых пишет лекционная статья? Он немного изощрённей, чем повторение квадрирования. В любом случае, возведение в квадрат является неизбежным, но оптимизация методом «скользящих окон» позволяет уменьшить накладные расходы умножения на это дополнительное значение с в конце формулы c2x+1 = (cx)2 x с.
Предположим, что у вас есть некоторое число, которое имеет несколько единичных бит в экспоненте, каждый единичный бит – бинарное представление, и вам придётся выполнить этот шаг c2x+1 вместо шага c2x, потому что для каждого нечетного числа вам придется умножить на c. Ребятам, чью статью мы обсуждаем, не хотелось производить это умножение на с слишком часто. Поэтому их план состоял в том, чтобы предварительно вычислять различные степени с.
Они создали своего рода таблицу, где располагались такие значения:
с1
с3
с7
…
с31
Они предварительно подсчитали значения в каждом из слотов этой таблицы. Затем, когда вы захотите сделать возведение в степень, вместо повторения квадрирования с умножением всякий раз на с, вы будете использовать другую формулу.
Например, если у вас имеется выражение с32x+y, то сначала вы можете выполнить возведение с в квадрат 5 раз, чтобы получить с в 32-й степени, а затем умножить полученное значение на сy.
Причем значение с32 вы можете взять из этой таблицы. Таким образом, вы видите, что мы возводим в квадрат столько же раз, сколько и раньше, но при этом нам не нужно умножать на c столько раз. Вы просто «выуживаете» значение из таблицы и вместо нескольких умножений умножаете всего один раз.
29:00 мин
Курс MIT «Безопасность компьютерных систем». Лекция 16: «Атаки через побочный канал», часть 2
Полная версия курса доступна здесь.
Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас оформив заказ или порекомендовав знакомым, 30% скидка для пользователей Хабра на уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps от $20 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).
VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps до декабря бесплатно при оплате на срок от полугода, заказать можно тут.
Dell R730xd в 2 раза дешевле? Только у нас 2 х Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 ТВ от $249 в Нидерландах и США! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5-2650 v4 стоимостью 9000 евро за копейки?

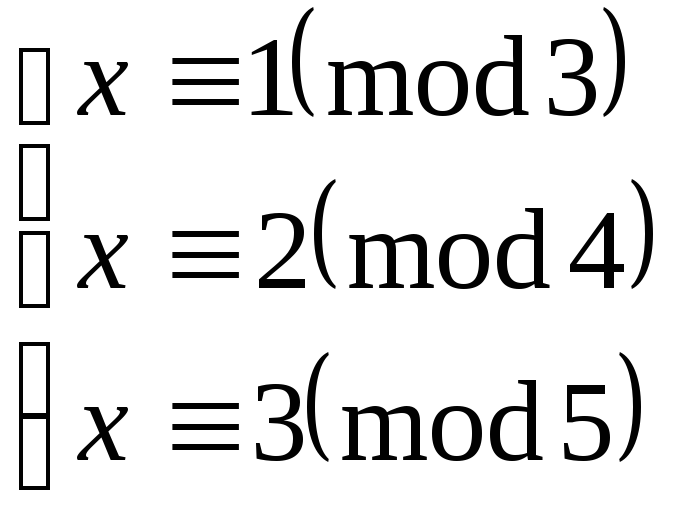
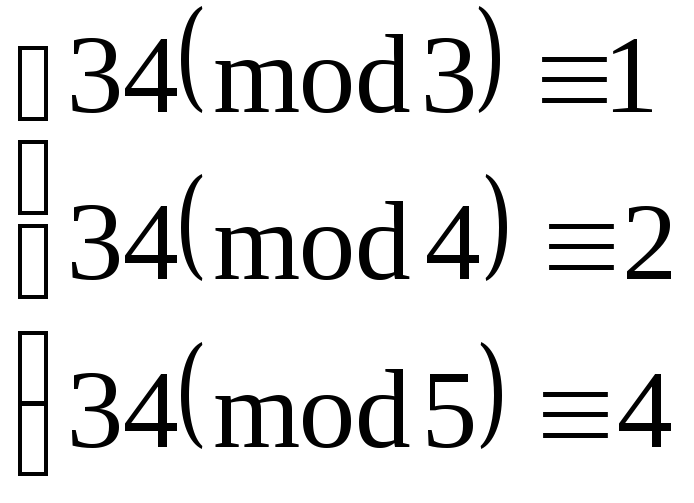
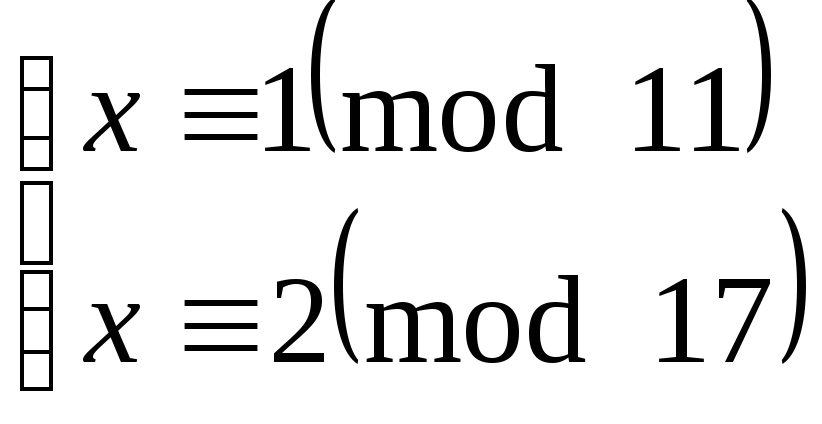




































![{displaystyle {begin{aligned}Q(X)&=prod _{i=1}^{k}(X-x_{i})\[6pt]Q_{i}(X)&={frac {Q(X)}{X-x_{i}}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b45587c61cab9fe77839ef0375254a9ec92ae1a1)



















![{begin{aligned}phi :k[M]/K&to prod _{{iin I}}k[M]/{mathrm {Ker}}F_{i}\phi (x+K)&=left(x+{mathrm {Ker}}F_{i}right)_{{iin I}}end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8176305b47702fd7343f6223ab0fbcf047f349da)

![{begin{aligned}Phi :k[M]&to prod _{{iin I}}k[M]/{mathrm {Ker}}F_{i}\Phi (x)&=left(x+{mathrm {Ker}}F_{i}right)_{{iin I}}end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd5d28277427dfee1e915ad6e9aeae4655e41f44)
![{begin{aligned}psi :k[M]&to prod _{{iin I}}k\psi (x)&=left[F_{i}(x)right]_{{iin I}}end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9598795d3005ba9a366342806215a44e9427b4c)