Содержание
Введение 3
Основная
часть 5
1История
создания 5
2Описание
алгоритма 5
2.1Создание ключей 6
2.2Шифрование и
расшифрование 6
7
2.3Пример
использования 7
Заключение 9
Список
использованных источников 10
Введение
Криптография – специальная система
изменения обычного письма, используемая
с целью сделать текст понятным лишь для
ограниченного числа лиц, знающих эту
систему [1].
Криптография – наука о защите информации
с использованием математических методов
[2].
Современная криптография включает в
себя:
-
симметричные
криптосистемы; -
асимметричные
криптосистемы; -
системы
электронной цифровой подписи (ЭЦП); -
хеш-функции;
-
управление
ключами; -
получение
скрытой информации; -
квантовая
криптография.
Симметричное шифрование — симметричными
называются алгоритмы, в которых для
шифрования и дешифрования используется
один и тот же (известный только отправителю
и получателю) секретный ключ.
Распространенные алгоритмы
симметричного шифрования:
-
AES (англ.
Advanced Encryption Standard) — американский стандарт
шифрования; -
ГОСТ
28147-89 — отечественный стандарт шифрования
данных; -
DES (англ.
Data Encryption Standard) — стандарт шифрования
данных в США до AES; -
3DES
(Triple-DES, тройной DES); -
IDEA
(англ. International Data Encryption
Algorithm); -
SEED —
корейский стандарт шифрования данных; -
Camellia —
сертифицированный для использовании
в Японии шифр; -
XTEA —
наиболее простой в реализации алгоритм
[3].
Асимметричные криптоалгоритмы призваны
в первую очередь устранить основной
недостаток симметричных криптосистем
– сложность управления и распространения
ключей.
Основой всех асимметричных криптоалгоритмов
является большая вычислительная
сложность восстановления открытого
текста без знания закрытого ключа.
Примеры асимметричных криптоалгритмов:
-
Diffie-Hellmann;
-
RSA
– Rivest, Shamir,
Adelman – основан на сложности
задачи разложения на множители больших
чисел за короткое время; -
El
Hamal; -
DSA
– Digital Signature algorithm, стандарт
США; -
ГОСТ Р
34.10 – 94, 2001, стандарты РФ [4].
В данном реферате подробно рассмотрим
ассиметричный криптоалгоритм шифрования
– алгоритм RSA.
Основная часть
Алгоритм RSA (буквенная аббревиатура от
фамилий Rivest, Shamir и Adleman) – криптографический
алгоритм с открытым ключом, основывающийся
на вычислительной сложности задачи
факторизации больших целых чисел.
Криптосистема RSA стала первой системой,
пригодной и для шифрования, и для цифровой
подписи.
-
История создания
Опубликованная в ноябре 1976 года статья
Уитфилда Диффи и Мартина Хеллмана «Новые
направления в криптографии» перевернула
представление о криптографических
системах, заложив основы криптографии
с открытым ключом. Разработанный
впоследствии алгоритм Диффи — Хеллмана
позволял двум сторонам получить общий
секретный ключ, используя незащищенный
канал связи. Однако этот алгоритм не
решал проблему аутентификации. Без
дополнительных средств пользователи
не могли быть уверены, с кем именно они
сгенерировали общий секретный ключ.
Изучив эту статью, трое учёных Рональд
Ривест (англ. Ronald Linn Rivest), Ади
Шамир (англ.
Adi Shamir) и Леонард Адлеман (англ.
Leonard Adleman) из Массачусетского Технологического
Института (MIT) приступили к поискам
математической функции, которая бы
позволяла реализовать сформулированную
Уитфилдом Диффи и Мартином Хеллманом
модель криптографической системы с
открытым ключом. После работы над более
чем 40 возможными вариантами, им удалось
найти алгоритм, основанный на различии
в том, насколько легко находить большие
простые числа и насколько сложно
раскладывать на множители произведение
двух больших простых чисел, получивший
впоследствии название RSA. Система была
названа по первым буквам фамилий её
создателей.
-
Описание алгоритма
Первым этапом любого асимметричного
алгоритма является создание пары ключей
– открытого и закрытого и распространение
открытого ключа «по всему миру».
-
Создание ключей
Для алгоритма RSA этап создания ключей
состоит из следующих операций:
-
Выбираются
два очень больших простых числа
and
.
-
Вычисляется
их произведение
,
которое называется модулем. -
Вычисляется
значение функции Эйлера от числа
:
-
Выбирается
произвольное число
(
),
взаимно простое со значением функции
.
Число
называется открытой экспонентой
-
С помощью
алгоритма Евклида вычисляется число
,
которое удовлетворяет условию
-
Пара
публикуется в качестве открытого ключа
RSA. -
Пара
играет роль закрытого ключа RSA и держится
в секрете.
-
Шифрование и расшифрование
Предположим, отправитель хочет послать
получателю сообщение
.
Сообщениями являются целые числа в
интервале от 0 до
,
т.е .
.
На рисунке 1 представлена схема алгоритма
RSA.
Рисунок 1 – Схема алгоритма RSA
Алгоритм Отправителя:
-
Взять
открытый ключ
получателя
-
Взять
открытый текст
-
Зашифровать
сообщение с использованием открытого
ключа получателя:
Алгоритм Получателя:
-
Принять
зашифрованное сообщение
-
Взять
свой закрытый ключ
-
Применить
закрытый ключ для расшифрования
сообщения:
Уравнения (1) и (2), на которых основана
схема RSA, определяют взаимно обратные
преобразования множества
[5].
-
Пример использования
В таблице 1 представлен пример использования
алгоритма RSA. Отправитель
отправил зашифрованное сообщение
«111111» и получатель, используя свой
закрытый ключ, расшифровал его.
Таблица 1 –
Поэтапное выполнение алгоритма RSA
|
Этап |
Описание |
Результат |
|
Генерация |
Выбрать |
|
|
Вычислить |
|
|
|
Вычислить |
|
|
|
Выбрать |
|
|
|
Вычислить |
|
|
|
Опубликовать |
|
|
|
Сохранить |
|
|
|
Шифрование |
Выбрать |
|
|
Вычислить |
|
|
|
Расшифрование |
Вычислить |
|
Заключение
В данном реферате был подробно рассмотрен
алгоритм ассиметричного шифрования
RSA. Была описана история
его создания, описаны алгоритмы создания
ключей, шифрования и расшифровки. Также
представлен пример практического
использования алгоритма RSA.
Список использованных источников
-
Семенов
Ю.А. Протоколы Internet // М.: Проспект, 2011. –
114 с.
-
Беляев
А.В. Методы и средства защиты информации
// ЧФ СПбГТУ, 2010. – 142с. -
Венбо М.
Современная криптография. Теория и
практика // М.: Вильямс, 2005. — 768 с. -
Шнайер
Б. Прикладная криптография. Протоколы,
алгоритмы, исходные тексты // М.: Триумф,
2002. — 816 с. -
Алгоритм
RSA // Интернет ресурс:
http://ru.wikipedia.org/wiki/Rsa
10
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ДИПЛОМНАЯ РАБОТА
на тему Применение
алгоритма RSA при шифровании потоков
данных
СОДЕРЖАНИЕ
|
Введение |
5 |
1.Постановка задачи |
10 |
|
2. |
11 |
|
2.1. Система шифрования RSA |
12 |
|
2.2.Сложность теоретико-числовых алгоритмов |
16 |
|
2.2.1. Алгоритм вычисления |
17 |
|
2.2.2. Алгоритм Евклида |
18 |
|
2.2.3. Алгоритм решения уравнения |
18 |
|
2.2.4. Алгоритм нахождения делителей |
21 |
|
3. |
23 |
|
3.1. Алгоритм, доказывающий непростоту |
24 |
|
3.2. Нахождение больших простых чисел |
26 |
|
3.3. Проверка большого числа на простоту |
30 |
|
4. |
37 |
|
4.1. Реализованные алгоритмы |
37 |
|
4.2. Анализ результатов |
38 |
|
5. |
39 |
|
5.1 Алгоритм |
39 |
|
5.2 Алгоритм и программа |
39 |
|
Заключение |
41 |
|
Список использованных источников |
42 |
|
Приложение 1. Листинг программы |
43 |
|
Приложение 2. Главная форма программы |
46 |
|
Приложение 3. Форма базы данных абонентов |
47 |
|
Приложение 4. Форма нахождения простых чисел и генерации |
48 |
ВВЕДЕНИЕ
Проблема защиты информации
путем ее преобразования, исключающего ее прочтение
посторонним лицом, волновала человеческий ум с давних
времен. История криптографии — ровесница истории человеческого
языка. Более того, первоначально письменность сама по себе была своеобразной
криптографической системой, так как в древних обществах ею владели только избранные. Священные книги древнего Египта, древней Индии тому примеры.
История криптографии условно можно разделить
на 4 этапа.
1) наивная криптография.
2) формальная криптография.
3) научная криптография.
4) компьютерная криптография.
Для наивной
криптографии (до нач. XVI века) характерно использование любых (обычно примитивных) способов
запутывания противника относительно содержания
шифруемых текстов. На начальном этапе для защиты
информации использовались методы кодирования и стеганографии, которые
родственны, но не тождественны криптографии.
Большинство из используемых
шифров сводились к перестановке или моноалфавитной подстановке. Одним из первых зафиксированных примеров является шифр Цезаря, состоящий в замене каждой буквы исходного текста на другую, отстоящую от нее в алфавите на определенное число позиций. Другой шифр, полибианский квадрат, авторство которого приписывается греческому писателю Полибию, является общей моноалфавитной подстановкой, которая проводится с помощью случайно заполненной алфавитом квадратной таблицейдля греческого алфавита размер
составляет 5×5). Каждая буква исходного текста
заменяется на букву, стоящую в квадрате снизу от нее.
Этап формальной криптографии (кон. XV века — нач. XX века)
связан с появлением формализованных и относительно стойких
к ручному криптоанализу шифров. В европейских странах
это произошло в эпоху Возрождения, когда развитие науки
и торговли вызвало спрос на надежные способы защиты информации.
Важная роль на этом этапе принадлежит Леону Батисте
Альберти, итальянскому архитектору, который одним из
первых предложил многоалфавитную подстановку. Данный шифр, получивший
имя дипломата XVI века Блеза Вижинера, состоял в последовательном «сложении» букв исходного текста с ключом (процедуру можно облегчить с помощью специальной таблицы). Его работа «Трактат о шифре» (1466) считается первой научной работой по криптологии.
Одной из первых печатных
работ, в которой обобщены и сформулированы известные на тот момент алгоритмы
шифрования является труд «Полиграфия» (1508 г.) немецкого аббата Иоганна
Трисемуса. Ему принадлежат два небольших, но важных
открытия: способ заполнения полибианского квадрата (первые
позиции заполняются с помощью легко запоминаемого ключевого
слова, остальные — оставшимися буквами алфавита) и
шифрование пар букв (биграмм).
Простым но стойким способом
многоалфавитной замены (подстановки биграмм) является шифр Плейфера, который
был открыт в начале XIX
века Чарльзом Уитстоном. Уитстону принадлежит и важное
усовершенствование — шифрование «двойным квадратом». Шифры
Плейфера и Уитстона использовались вплоть до первой мировой
войны, так как с трудом поддавались ручному криптоанализу.
В XIX веке голландец Керкхофф сформулировал главное требование
к криптографическим системам, которое остается актуальным и поныне: секретность
шифров должна быть основана на секретности ключа,
но не алгоритма.
Наконец, последним словом в
донаучной криптографии, которое обеспечили еще более высокую криптостойкосить,
а также позволило автоматизировать (в смысле механизировать) процесс шифрования стали роторные криптосистемы.
Одной из первых подобных систем стала
изобретенная в 1790 году Томасом Джефферсоном, будущим президентом США механическая машина. Многоалфавитная
подстановка с помощью роторной
машины реализуется вариацией взаимного положения вращающихся роторов, каждый из
которых осуществляет «прошитую» в нем подстановку.
Практическое
распространение роторные машины получили только в начале XX века. Одной из
первых практически используемых машин, стала немецкая Enigma, разработанная в
1917 году Эдвардом Хеберном и усовершенствованная Артуром Кирхом. Роторные машины
активно использовались во время второй мировой войны. Помимо немецкой машины
Enigma использовались также устройства Sigaba (США), Турех (Великобритания),
Red, Orange и Purple2 (Япония). Роторные системы -вершина формальной
криптографии так как относительно просто реализовывали очень стойкие шифры.
Успешные криптоатаки на роторные системы стали возможны только с появлением ЭВМ
в начале 40-х годов.
Главная отличительная черта
научной криптографии (30-е — 60-е годы XX века) — появление криптосистем со строгим
математическим обоснованием криптостойкости. К началу 30-х годов окончательно
сформировались разделы математики, являющиеся научной основой криптологии:
теория вероятностей и математическая статистика, общая алгебра, теория чисел,
начали активно развиваться теория алгоритмов, теория информации, кибернетика.
Своеобразным водоразделом стала работа Клода Шеннона «Теория связи в секретных
системах» (1949), где сформулированы теоретические принципы криптографической
защиты информации. Шеннон ввел понятия «рассеивание» и «перемешивание»,
обосновал возможность создания сколь угодно стойких криптосистем.
В 60-х годах ведущие
криптографические школы подошли к созданию блочных шифров, еще более стойких по
сравнению с роторными криптосистемами, однако допускающие практическую
реализацию только в виде цифровых электронных устройств.
Компьютерная криптография
(с 70-х годов XX века) обязана своим появлением вычислительным средствам с
производительностью, достаточной для реализации критосистем, обеспечивающих при
большой скорости шифрования на несколько порядков более высокую
криптостойкость, чем «ручные» и «механические» шифры.
Первым классом
криптосистем, практическое применение которых стало возможно с появлением
мощных и компактных вычислительных средств, стали блочные шифры. В 70-е годы
был разработан американский стандарт шифрования DES (принят в 1978 году). Один из его авторов, Хорст Фейстел (сотрудник IBM), описал модель блочных шифров, на основе которой были построены
другие, более стойкие симметричные криптосистемы, в том числе отечественный
стандарт шифрования ГОСТ 28147-89.
С появлением DES обогатился и криптоанализ, для атак на американский алгоритм был
создано несколько новых видов криптоанализа (линейный, дифференциальный и
т.д.), практическая реализация которых опять же была возможна только с
появлением мощных вычислительных систем.
В середине 70-х годов
произошел настоящий прорыв в современной криптографии — появление асимметричных
криптосистем, которые не требовали передачи секретного ключа между сторонами.
Здесь отправной точкой принято считать работу, опубликованную Уитфилдом Диффи и
Мартином Хеллманом в 1976 году под названием «Новые направления в современной
криптографии». В ней впервые сформулированы принципы обмена шифрованной
информацией без обмена секретным ключом. Независимо к идее асимметричных
криптосистем подошел Ральф Меркли. Несколькими годами позже Рон Ривест, Ади
Шамир и Леонард Адлеман открыли систему RSA,
первую практическую асимметричную криптосистему, стойкость которой была
основана на проблеме факторизации больших простых чисел. Асимметричная
криптография открыла сразу несколько новых прикладных направлений, в частности
системы электронной цифровой подписи (ЭЦП) и электронных денег.
В 80-90-е годы появились
совершенно новые направления криптографии: вероятностное шифрование, квантовая
криптография и другие. Осознание их практической ценности еще впереди.
Актуальной остается и задача совершенствования симметричных криптосистем. В
80-90-х годах были разработаны нефейстеловские шифры (SAFER, RC6 и др.), а в 2000 году после
открытого международного конкурса был принят новый национальный стандарт
шифрования США — AES.
1. ПОСТАНОВКА
ЗАДАЧИ
Безопасность передачи
данных по каналам связи является актуальной. Современные компьютерные сети не
исключение. К сожалению, в сетевых операционных системах (Windows NT/XP, Novell и т.д.) иностранного производства, как следствие, из-за экспортных
соображений уровень алгоритмов шифрования заметно снижен.
Задача: исследовать
современные методы шифрования и их приложимость к шифрованию потоков данных.
Разработать собственную библиотеку алгоритмов шифрования и программный продукт,
демонстрирующий работу этих алгоритмов при передаче данных в сети.
2. АЛГОРИТМ RSA
Труды Евклида и Диофанта, Ферма и Эйлера, Гаусса,
Чебышева и Эрмита содержат остроумные и весьма эффективные алгоритмы решения
диофантовых уравнений, выяснения разрешимости сравнений, построения больших по
тем временам простых чисел, нахождения наилучших приближений и т.д. В последние
два десятилетия, благодаря в первую очередь запросам криптографии и широкому
распространению ЭВМ, исследования по алгоритмическим вопросам теории чисел
переживают период бурного и весьма плодотворного развития.
Вычислительные машины и электронные средства
связи проникли практически во все сферы человеческой деятельности. Немыслима
без них и современная криптография. Шифрование и дешифрование текстов можно
представлять себе как процессы переработки целых чисел при помощи ЭВМ, а
способы, которыми выполняются эти операции, как некоторые функции,
определённые на множестве целых чисел. Всё это делает естественным появление в
криптографии методов теории чисел. Кроме того, стойкость ряда современных
криптосистем обосновывается только сложностью некоторых теоретико-числовых задач.
Но возможности ЭВМ имеют определённые границы.
Приходится разбивать длинную цифровую последовательность на блоки ограниченной
длины и шифровать каждый такой блок отдельно. Мы будем считать в дальнейшем,
что все шифруемые целые числа неотрицательны и по величине меньше некоторого
заданного (скажем, техническими ограничениями) числа m. Таким же условиям будут
удовлетворять и числа, получаемые в процессе шифрования. Это позволяет считать
и те, и другие числа элементами кольца вычетов .
Шифрующая функция при этом может рассматриваться как взаимнооднозначное
отображение колец вычетов
а число представляет собой сообщение
в зашифрованном виде.
Простейший шифр такого рода — шифр замены,
соответствует отображению при некотором
фиксированном целом k. Подобный шифр использовал еще Юлий Цезарь. Конечно, не каждое
отображение подходит для целей надежного сокрытия
информации.
В 1978 г. американцы Р. Ривест, А. Шамир и Л.
Адлеман (R.L.Rivest. A.Shamir. L.Adleman) предложили
пример функции , обладающей рядом
замечательных достоинств. На её основе была построена реально используемая
система шифрования, получившая название по первым буквам имен авторов -система
RSA. Эта функция
такова, что
1) существует
достаточно быстрый алгоритм вычисления значений ;
2) существует
достаточно быстрый алгоритм вычисления значений обратной функции ;
3) функция
обладает некоторым «секретом», знание
которого позволяет быстро вычислять значения ; в
противном же случае вычисление становится трудно разрешимой
в вычислительном отношении задачей, требующей для своего решения столь много
времени, что по его
прошествии зашифрованная информация перестает представлять интерес для лиц,
использующих отображение в качестве шифра.
Еще до выхода из печати статьи копия доклада в
Массачусетском Технологическом институте, посвящённого системе RSA. была послана известному
популяризатору математики М. Гарднеру, который в 1977 г. в журнале Scientific American опубликовал
статью посвящённую этой системе шифрования. В русском переводе заглавие статьи
Гарднера звучит так: Новый вид шифра, на расшифровку которого потребуются миллионы
лет. Именно эта статья сыграла важнейшую роль в распространении информации об RSA, привлекла к
криптографии внимание широких кругов неспециалистов и фактически способствовала
бурному прогрессу этой области, произошедшему в последовавшие 20 лет.
2.1. система шифрования RSA
Пусть и
натуральные числа. Функция
реализующая схему RSA, устроена следующим
образом
. (1)
Для расшифровки сообщения достаточно
решить сравнение
.
(2)
При некоторых условиях на и
это сравнение имеет единственное решение
.
Для того, чтобы описать эти условия и объяснить,
как можно найти решение, нам потребуется одна теоретико-числовая функция, так
называемая функция Эйлера. Эта функция натурального аргумента обозначается
и
равняется количеству целых чисел на отрезке от 1 до ,
взаимно простых с . Так
и
для любого простого числа
и натурального
.
Кроме того, для любых натуральных взаимно простых
и
. Эти
свойства позволяют легко вычислить значение , если
известно разложение числа на простые
сомножители.
Если показатель степени в
сравнении (2) взаимно прост с , то сравнение (2)
имеет единственное решение. Для того, чтобы найти его, определим целое число , удовлетворяющее условиям
.
(3)
Такое число существует, поскольку , и
притом единственно. Здесь и далее символом будет
обозначаться наибольший общий делитель чисел и
. Классическая теорема Эйлера, утверждает,
что для каждого числа , взаимно простого с
, выполняется сравнение
и, следовательно.
. (4)
Таким образом, в предположении ,
единственное решение сравнения (2) может быть найдено в виде
.
(5)
Если
дополнительно предположить, что число состоит
из различных простых сомножителей, то сравнение (5) будет выполняться и без
предположения . Действительно, обозначим
и
. Тогда
делится на
, а из
(2) следует, что . Подобно (4), теперь легко
находим . А кроме того, имеем
. Получившиеся сравнения в силу
дают нам (5).
Функция (1), принятая в системе RSA, может быть вычислена достаточно быстро.
Обратная к функция
вычисляется
по тем же правилам, что и , лишь с заменой
показателя степени на
. Таким
образом, для функции (1) будут выполнены указанные выше свойства 1) и 2).
Для вычисления функции (1) достаточно знать лишь числа и
.
Именно они составляют открытый ключ для шифрования. А вот для вычисления
обратной функции требуется знать число . оно и
является «секретом», о котором речь идёт в пункте в). Казалось бы. ничего не
стоит. зная число . разложить его на простые
сомножители, вычислить затем с помощью известных правил значение и, наконец, с помощью (3) определить
нужное число . Все шаги этого вычисления могут быть реализованы
достаточно быстро, за исключением первого. Именно разложение числа на простые множители и составляет
наиболее трудоемкую часть вычислений. В теории чисел несмотря на многолетнюю её
историю и на очень интенсивные поиски в течение последних 20 лет, эффективный
алгоритм разложения натуральных чисел на множители так и не найден. Конечно,
можно, перебирая все простые числа до , и.
деля на них , найти требуемое разложение. Но,
учитывая, что количество простых в этом промежутке, асимптотически равно , находим, что при
, записываемом 100 десятичными цифрами,
найдётся не менее простых чисел, на которые
придётся делить при разложении его на
множители. Очень грубые прикидки показывают, что компьютеру, выполняющему
миллион делений в секунду, для разложения числа таким
способом на простые сомножители потребуется не менее, чем лет. Известны и более эффективные способы
разложения целых чисел на множители, чем простой перебор простых делителей, но
и они работают очень медленно.
Авторы схемы RSA предложили выбирать число в виде произведения двух простых
множителей и
,
примерно одинаковых по величине. Так как
, (6)
то единственное условие на выбор показателя степени в отображении (1) есть
.
(7)
Итак, лицо, заинтересованное в организации шифрованной переписки с
помощью схемы RSA, выбирает два
достаточно больших простых числа и
. Перемножая их, оно находит число
. Затем выбирается число
, удовлетворяющее условиям (7),
вычисляется с помощью (6) число и с помощью (3) —
число . Числа
и
публикуются, число
остается секретным. Теперь любой может
отправлять зашифрованные с помощью (1) сообщения организатору этой системы, а
организатор легко сможет расшифровывать их с помощью (5).
Для иллюстрации своего метода Ривест, Шамир и
Адлеман зашифровали таким способом некоторую английскую фразу. Сначала она
стандартным образом (а=01, b=02, …. z=26, пробел=00) была записана в виде целого числа , а затем зашифрована с помощью
отображения (1) при
m=11438162575788886766932577997614661201021829672124236256256184293570
6935245733897830597123563958705058989075147599290026879543541
и . Эти два числа были
опубликованы, причем дополнительно сообщалось, что . где
и
—
простые числа, записываемые соответственно 64 и 65 десятичными знаками.
Первому, кто расшифрует соответствующее сообщение

была обещана награда в 100$.
Эта история завершилась спустя 17 лет в 1994 г., когда
D. Atkins, M. Graff, А. К. Lenstra и Р. С. Leyland сообщили о
расшифровке фразы. Числа и
оказались равными
,
.
Этот замечательный результат (разложение на множители
129-значного десятичного числа) был достигнут благодаря использованию
алгоритма разложения чисел на множители, называемого методом квадратичного решета.
Выполнение вычислений потребовало колоссальных ресурсов. В работе, возглавлявшейся
четырьмя авторами проекта, и продолжавшейся после предварительной теоретической
подготовки примерно 220 дней, на добровольных началах участвовало около 600
человек и примерно 1600 компьютеров, объединённых сетью Internet. Наконец, отметим, что
премия в 100$ была передана в Free Software Foundation.
2.2.Сложность теоретико-числовых алгоритмов
Сложность алгоритмов теории чисел обычно принято
измерять количеством арифметических операций (сложений, вычитаний, умножений и
делений с остатком), необходимых для выполнения всех действий, предписанных
алгоритмом. Впрочем, это определение не учитывает величины чисел, участвующих в
вычислениях. Ясно, что перемножить два стозначных числа значительно сложнее,
чем два однозначных, хотя при этом и в том, и в другом случае выполняется лишь
одна арифметическая операция. Поэтому иногда учитывают ещё и величину чисел,
сводя дело к так называемым битовым операциям, т. е. оценивая количество необходимых
операций с цифрами 0 и 1, в двоичной записи чисел.
Говоря о сложности алгоритмов, мы будем иметь в
виду количество арифметических операций. При построении эффективных алгоритмов
и обсуждении верхних оценок сложности обычно хватает интуитивных понятий той
области математики, которой принадлежит алгоритм. Формализация же этих понятий
требуется лишь тогда, когда речь идёт об отсутствии алгоритма или
доказательстве нижних опенок сложности.
Приведем теперь примеры достаточно быстрых
алгоритмов с опенками их сложности. Здесь и в дальнейшем мы не будем придерживаться
формального описания алгоритмов, стараясь в первую очередь объяснить смысл
выполняемых действий.
Следующий алгоритм вычисляет за
арифметических
операций. При этом, конечно, предполагается, что натуральные числа и
не
превосходят по величине .
2.2.1. Алгоритм вычисления
1) Представим в двоичной системе счисления
, где
, цифры
в двоичном представлении, равны 0 или 1, .
2) Положим и затем для
вычислим
.
3) есть искомый вычет
.
Справедливость этого алгоритма вытекает из сравнения
,
легко
доказываемого индукцией по .
Так как каждое вычисление на шаге 2 требует не
более трёх умножений по модулю и этот шаг выполняется
раз, то сложность алгоритма может быть
оценена величиной .
Второй алгоритм — это классический алгоритм Евклида
вычисления наибольшего общего делителя целых чисел. Мы предполагаем заданными
два натуральных числа и
и
вычисляем их наибольший общий делитель .
2.2.2. Алгоритм Евклида
1) Вычислим — остаток от деления числа
на
,
,
.
2) Если , то
есть
искомое число.
3) Если , то заменим пару чисел
парой
и
перейдем к
шагу 1.
Теорема 1. При вычислении наибольшего общего
делителя с помощью алгоритма Евклида будет
выполнено не более операций деления с остатком,
где есть количество цифр в десятичной записи
меньшего из чисел и
.
Доказательство. Положим и
определим — последовательность делителей,
появляющихся в процессе выполнения шага 1 алгоритма Евклида. Тогда
.
Пусть также ,
,
,
, — последовательность Фибоначчи.
Индукцией по от
до
легко доказывается неравенство
. А так как
, то
имеем неравенства и
.
Немного подправив алгоритм Евклида, можно
достаточно быстро решать сравнения при условии, что
. Эта задача равносильна поиску целых решений
уравнения .
2.2.3. Алгоритм
решения уравнения
0) Определим матрицу 
1) Вычислим — остаток
от деления числа на
,
,
.
2) Если , то второй столбец матрицы
даёт вектор
решений уравнения.
3) Если , то заменим матрицу
матрицей

4) Заменим пару
чисел парой
и
перейдем к шагу 1.
Если обозначить через матрицу
, возникающую в процессе работы алгоритма
перед шагом 2 после делений с остатком (шаг 1), то
в обозначениях из доказательства теоремы 1 в этот момент выполняется векторное
равенство . Поскольку числа
и
взаимно просты, имеем
, и это доказывает, что алгоритм
действительно даёт решение уравнения . Буквой
мы обозначили количество делений с
остатком, которое в точности такое же, как и в алгоритме Евклида.
Три приведённых выше алгоритма относятся к
разряду так называемых полиномиальных алгоритмов. Это название носят
алгоритмы, сложность которых оценивается сверху степенным образом в
зависимости от длины записи входящих чисел. Если наибольшее из чисел,
подаваемых на вход алгоритма, не превосходит , то
сложность алгоритмов этого типа оценивается величиной ,
где — некоторая абсолютная постоянная. Во
всех приведённых выше примерах .
Полиномиальные алгоритмы в теории чисел — большая
редкость. Да и опенки сложности алгоритмов чаше всего опираются на какие-либо
не доказанные, но правдоподобные гипотезы, обычно относящиеся к аналитической
теории чисел.
Для некоторых задач эффективные алгоритмы вообще
не известны. Иногда в таких случаях все же можно предложить последовательность
действий, которая, «если повезет», быстро приводит к требуемому результату.
Существует класс так называемых вероятностных алгоритмов, которые дают
правильный результат, но имеют вероятностную опенку времени работы. Обычно
работа этих алгоритмов зависит от одного или нескольких параметров. В худшем
случае они работают достаточно долго. Но удачный выбор параметра определяет
быстрое завершение работы. Такие алгоритмы, если множество «хороших» значений
параметров велико, на практике работают достаточно эффективно, хотя и не имеют
хороших опенок сложности.
Мы будем иногда использовать слова
детерминированный алгоритм, чтобы отличать алгоритмы в обычном смысле от
вероятностных алгоритмов.
Как пример, рассмотрим вероятностный алгоритм,
позволяющий эффективно находить решения полиномиальных сравнений по простому
модулю. Пусть — простое число, которое
предполагается большим, и — многочлен, степень
которого предполагается ограниченной. Задача состоит в отыскании решений
сравнения
. (8)
Например, речь может идти о решении квадратичных сравнений, если
степень многочлена равна 2. Другими словами, мы
должны отыскать в поле все элементы, удовлетворяющие
уравнению .
Согласно малой теореме Ферма, все элементы поля являются однократными корнями многочлена
. Поэтому, вычислив наибольший общий
делитель , мы найдем многочлен
, множество корней которого в поле
совпадает с множеством корней многочлена
, причем все эти корни однократны. Если
окажется, что многочлен имеет нулевую степень,
т. е. лежит в поле , это будет означать, что
сравнение (8) не имеет решений.
Для вычисления многочлена удобно
сначала вычислить многочлен , пользуясь
алгоритмом, подобным описанному выше алгоритму возведения в степень (напомним,
что число предполагается большим). А затем с
помощью аналога алгоритма Евклида вычислить . Всё
это выполняется за полиномиальное количество арифметических операций.
Таким образом, обсуждая далее задачу нахождения решений
сравнения (8), мы можем предполагать, что в кольце многочленов справедливо равенство
2.2.4. Алгоритм нахождения
делителей многочлена в кольце
1) Выберем каким-либо способом элемент .
2) Вычислим
наибольший общий делитель 
3) Если многочлен окажется собственным делителем
, то многочлен
распадётся
на два множителя и с каждым из них независимо нужно будет проделать все
операции, предписываемые настоящим алгоритмом для многочлена .
4) Если окажется, что или
, следует перейти к шагу 1 и. выбрав новое
значение , продолжить выполнение алгоритма.
Количество операций на шаге 2 оценивается величиной
, если вычисления проводить так, как это
указывалось выше при нахождении . Выясним теперь, сколь
долго придётся выбирать числа , пока на шаге 2 не
будет найден собственный делитель .
Количество решений
уравнения в поле
не превосходит
. Это означает, что подмножество
элементов
,
удовлетворяющих условиям
,
состоит не менее,
чем из элементов. Учитывая теперь, что каждый
ненулевой элемент удовлетворяет одному из
равенств , либо
, заключаем,
что для одно из чисел
будет
корнем многочлена , а другое — нет. Для таких
элементов многочлен
,
определённый на шаге 2 алгоритма, будет собственным делителем многочлена .
Итак, существует не менее «удачных»
выборов элемента , при которых на шаге 2
алгоритма многочлен распадётся на два собственных
множителя. Следовательно, при «случайном» выборе элемента , вероятность того, что многочлен не
разложится на множители после повторений шагов
алгоритма 1-4. не превосходит . Вероятность с ростом
убывает очень быстро. И действительно, на
практике этот алгоритм работает достаточно эффективно.
Заметим, что при опенке вероятности мы
использовали только два корня многочлена . При
эта вероятность, конечно, еще меньше.
Более тонкий анализ с использованием опенок А. Вейля для сумм характеров
показывает, что вероятность для многочлена не
распасться на множители при однократном проходе шагов алгоритма 1-4. не превосходит
. Здесь постоянная в
зависит от
.
Если в сравнении (8) заменить простой модуль составным модулем
, то задача нахождения решений
соответствующего сравнения становится намного более сложной. Известные
алгоритмы её решения основаны на сведении сравнения к совокупности сравнений
(8) по простым модулям — делителям , и. следовательно, они
требуют разложения числа то на простые сомножители, что, как уже указывалось,
является достаточно трудоемкой задачей.
3. КАЧЕСТВЕННАЯ
ТЕОРИЯ АЛГОРИТМА RSA
Существует довольно эффективный способ убедиться,
что заданное число является составным, не разлагая это число на множители.
Согласно малой теореме Ферма, если число простое,
то для любого целого , не делящегося на
, выполняется сравнение
.
(9)
Если же при каком-то это сравнение
нарушается, можно утверждать, что — составное. Проверка
(9) не требует больших вычислений, это следует из алгоритма 1. Вопрос только в
том, как найти для составного целое число
, не удовлетворяющее (9). Можно, например,
пытаться найти необходимое число , испытывая все целые
числа подряд, начиная с 2. Или попробовать выбирать эти числа случайным образом
на отрезке .
К сожалению, такой подход не всегда даёт то, что хотелось бы. Имеются
составные числа , обладающие свойством (9) для
любого целого с условием
. Такие числа называются числами
Кармайкла. Рассмотрим, например, число . Так
как 560 делится на каждое из чисел 2, 10, 16, то с помощью малой теоремы Ферма
легко проверить, что 561 есть число Кармайкла. Можно доказать, что любое из
чисел Кармайкла имеет вид , где все простые
различны, причем
делится
на каждую разность . Лишь недавно, была решена
проблема о бесконечности множества таких чисел.
В 1976 г. Миллер предложил заменить проверку (9)
проверкой несколько иного условия. Если —
простое число, , где
нечётно,
то согласно малой теореме Ферма для каждого с
условием хотя бы одна из скобок в произведении
делится на . Обращение этого свойства можно
использовать, чтобы отличать составные числа от простых.
Пусть — нечётное составное
число, , где
нечётно.
Назовем целое число ,
,
«хорошим» для , если нарушается одно из двух
условий:
1) не делится на
;
2) или существует целое
,
,
такое, что
.
Из сказанного ранее следует, что для простого
числа не существует хороших чисел
. Если же
составное
число, то, как доказал Рабин, их существует не менее .
Теперь можно построить вероятностный алгоритм,
отличающий составные числа от простых.
3.1. Алгоритм, доказывающий
непростоту числа
1) Выберем случайным
образом число ,
, и
проверим для
этого числа указанные выше свойства 1) и 2) п.2.
2) Если хотя бы одно
из них нарушается, то число составное.
3) Если выполнены
оба условия 1) и 2) п.2, возвращаемся к шагу 1.
Из сказанного выше следует, что составное число
не будет определено как составное после однократного выполнения шагов 1-3 с
вероятностью не большей . А вероятность не
определить его после повторений не превосходит
. т. е. убывает очень быстро.
Миллер предложил детерминированный алгоритм
определения составных чисел, имеющий сложность ,
однако справедливость его результата зависит от недоказанной в настоящее время
так называемой расширенной гипотезы Римана. Согласно этому алгоритму достаточно
проверить условия 1) и 2) п.2 для всех целых чисел ,
. Если при каком-нибудь
из указанного промежутка нарушается одно
из условий а) или б), число составное. В противном
случае оно будет простым или степенью простого числа. Последняя возможность,
конечно, легко проверяется.
Напомним некоторые понятия, необходимые для
формулировки расширенной гипотезы Римана. Они понадобятся нам и в дальнейшем.
Пусть — целое число. Функция
называется характером Дирихле по модулю
, или просто характером, если эта функция
периодична с периодом , отлична от нуля только на
числах, взаимно простых с , и мультипликативна,
т. е. для любых целых выполняется равенство
. Для каждого
существует
ровно характеров Дирихле. Они образуют группу
по умножению. Единичным элементом этой группы является так называемый главный
характер , равный 1 на всех числах, взаимно простых
с , и 0 на остальных целых числах. Порядком
характера называется его порядок как элемента мультипликативной группы
характеров.
С каждым
характером может быть связана так называемая — функция
Дирихле — функция комплексного переменного , определённая
рядом
и может быть аналитически продолжена на
всю комплексную плоскость. Следующее соотношение связывает
L — функцию,
отвечающую главному характеру, с дзета-функцией Римана 
Расширенная гипотеза Римана утверждает, что комплексные нули всех L -функций
Дирихле, расположенные в полосе , лежат на прямой
. В настоящее время не доказана даже
простейшая форма этой гипотезы — классическая гипотеза Римана, утверждающая
такой же факт о нулях дзета-функции.
В 1952 г. Анкени с помощью расширенной гипотезы
Римана доказал, что для каждого простого числа существует
квадратичный невычет , удовлетворяющий неравенствам
. Константа 70 была сосчитана позднее.
Именно это утверждение и лежит в основе алгоритма Миллера. В 1957 г. Берджесс
доказал существование такого невычета без использования расширенной гипотезы
Римана, но с худшей оценкой , справедливой при
любом положительном и
,
большем некоторой границы, зависящей от.
Алгоритм Миллера принципиально отличается от
алгоритма 2.1., так как полученное с его помощью утверждение о том, что число — составное, опирается на недоказанную
расширенную гипотезу Римана и потому может быть неверным. В то время как
вероятностный алгоритм 2.1. даёт совершенно правильный ответ для составных
чисел. Несмотря на отсутствие оценок сложности, на практике он работает вполне
удовлетворительно.
3.2. Нахождение больших простых чисел
Конечно же, большие простые числа можно строить
сравнительно быстро. При этом можно обеспечить их случайное распределение в
заданном диапазоне величин. В противном случае теряла бы всякий практический
смысл система шифрования RSA. Наиболее эффективным средством построения простых чисел является
несколько модифицированная малая теорема Ферма.
Теорема 2. Пусть —
нечётные натуральные числа, , причем для каждого
простого делителя числа
существует
целое число такое, что

Тогда каждый простой делитель числа
удовлетворяет сравнению
.
Доказательство. Пусть —
простой делитель числа , a
— некоторый
делитель . Из условий (10) следует, что в поле
вычетов справедливы соотношения
.
(11)
Обозначим буквой порядок элемента
в мультипликативной группе поля
. Первые два из соотношений (11) означают,
что входит в разложение на простые множители
числа в степени такой же, как и в разложение
, а последнее — что
делится на
. Таким
образом, каждый простой делитель числа входит
в разложение в степени не меньшей, чем в
, так что
делится
на . Кроме того,
четно.
Теорема 2 доказана.
Следствие. Если выполнены условия теоремы 2 и , то
—
простое число.
Действительно, пусть равняется
произведению не менее двух простых чисел. Каждое из них, согласно утверждению
теоремы 2, не меньше, чем . Но тогда
. Противоречие и доказывает следствие.
Покажем теперь, как с помощью последнего
утверждения, имея большое простое число , можно
построить существенно большее простое число .
Выберем для этого случайным образом чётное число на промежутке
и положим
. Затем
проверим число на отсутствие малых простых
делителей, разделив его на малые простые числа; испытаем некоторое количество раз с помощью
алгоритма 5. Если при этом выяснится, что —
составное число, следует выбрать новое значение и
опять повторить вычисления. Так следует делать до тех пор, пока не будет
найдено число , выдержавшее испытания алгоритмом
5 достаточно много раз. В этом случае появляется надежда на то, что — простое число, и следует попытаться
доказать простоту с помощью тестов теоремы 2.
Для этого можно случайным образом выбирать число , и проверять для него выполнимость
соотношений
.
(12)
Если при
выбранном эти соотношения выполняются, то, согласно
следствию из теоремы 2, можно утверждать, что число простое.
Если же эти условия нарушаются, нужно выбрать другое значение и повторять эти операции до тех пор, пока
такое число не будет обнаружено.
Предположим, что построенное число действительно является простым.
Зададимся вопросом, сколь долго придётся перебирать числа , пока не будет найдено такое, для
которого будут выполнены условия (12). Заметим, что для простого числа первое условие (12), согласно малой
теореме Ферма, будет выполняться всегда. Те же числа ,
для которых нарушается второе условие (12), удовлетворяют сравнению . Как известно, уравнение
в поле вычетов
имеет
не более решений. Одно из них
. Поэтому на промежутке
имеется не более
чисел,
для которых не выполняются условия (12). Это означает, что, выбирая случайным
образом числа на промежутке
, при простом
можно
с вероятностью большей, чем , найти число
, для которого будут выполнены условия
теоремы 2, и тем доказать, что действительно является
простым числом.
Заметим, что построенное таким способом простое число будет удовлетворять неравенству
, т. е. будет записываться вдвое большим
количеством цифр, чем исходное простое число .
Заменив теперь число на найденное простое число
и повторив с этим новым
все указанные выше действия, можно
построить еще большее простое число. Начав с какого-нибудь простого числа,
скажем, записанного 10 десятичными цифрами (простоту его можно проверить,
например, делением на маленькие табличные простые числа), и повторив указанную
процедуру достаточное число раз. можно построить простые числа нужной величины.
Обсудим теперь некоторые теоретические вопросы, возникающие в
связи с нахождением числа , удовлетворяющего
неравенствам , и такого, что
— простое число. Прежде всего, согласно
теореме Дирихле, доказанной еще в 1839 г., прогрессия ,
содержит бесконечное количество простых
чисел. Нас интересуют простые числа, лежащие недалеко от начала прогрессии.
Опенка наименьшего простого числа в арифметической прогрессии была получена в
1944 г. Ю. В. Линником. Соответствующая теорема утверждает, что наименьшее
простое число в арифметической прогрессии не
превосходит , где
—
некоторая достаточно большая абсолютная постоянная.
Таким образом, в настоящее время никаких
теоретических гарантий для существования простого числа не
существует. Тем не менее опыт вычислений на ЭВМ показывает, что простые числа
в арифметической прогрессии встречаются достаточно близко к её началу. Упомянем
в этой связи гипотезу о существовании бесконечного количества простых чисел с условием, что число
также простое, т. е. простым является уже
первый член прогрессии.
Очень важен в связи с описываемым методом построения
простых чисел также вопрос о расстоянии между соседними простыми числами в
арифметической прогрессии. Ведь убедившись, что при некотором число
составное,
можно следующее значение взять равным
и действовать так далее, пока не будет
найдено простое число . И если расстояние между
соседними простыми числами в прогрессии велико, нет надежды быстро построить
нужное число . Перебор чисел
до
того момента, как мы наткнемся на простое число окажется
слишком долгим. В более простом вопросе о расстоянии между соседними простыми
числами и
в
натуральном ряде доказано лишь, что 
очень хорошо для наших целей. Вместе с тем существует так называемая гипотеза
Крамера (1936 г.), что , дающая вполне
приемлемую опенку. Примерно такой же результат следует и из расширенной
гипотезы Римана. Вычисления на ЭВМ показывают, что простые числа в
арифметических прогрессиях расположены достаточно плотно.
В качестве итога обсуждения в этом пункте
подчеркнём следующее: если принять на веру, что наименьшее простое число, а
также расстояние между соседними простыми числами в прогрессии при
оцениваются
величиной , то описанная схема построения больших
простых чисел имеет полиномиальную опенку сложности. Кроме того, несмотря на
отсутствие теоретических опенок времени работы алгоритмов, отыскивающих простые
числа в арифметических прогрессиях со сравнительно большой разностью, на
практике эти алгоритмы работают вполне удовлетворительно. На обычном
персональном компьютере без особых затрат времени строятся таким способом
простые числа порядка .
Конечно, способ конструирования простых чисел для
использования в схеме RSA должен быть массовым, а сами простые числа должны быть в каком-то
смысле хорошо распределёнными. Это вносит ряд дополнительных осложнений в
работу алгоритмов.
Наконец, отметим, что существуют методы
построения больших простых чисел, использующие не только простые делители , но и делители чисел
. В основе их лежит использование последовательностей
целых чисел, удовлетворяющих линейным рекуррентным уравнениям различных
порядков. Отметим, что последовательность , члены
которой присутствуют в формулировке малой теоремы Ферма, составляет решение
рекуррентного уравнения первого порядка .
3.3. Проверка большого числа на простоту
Есть некоторое отличие в постановках задач
предыдущего и настоящего пунктов. Когда мы строим простое число , мы обладаем некоторой дополнительной
информацией о нем, возникающей в процессе построения. Например, такой
информацией является знание простых делителей числа . Эта
информация иногда облегчает доказательство простоты .
В этом пункте мы предполагаем лишь, что нам задано некоторое число
, например, выбранное случайным образом на
каком-то промежутке, и требуется установить его простоту, или доказать, что
оно является составным. Эту задачу за полиномиальное количество операций решает
указанный в п. 3 алгоритм Миллера. Однако, справедливость полученного с его
помощью утверждения зависит от недоказанной расширенной гипотезы Римана. Если
число выдержало испытания алгоритмом 5 для 100
различных значений параметра , то, по-видимому,
можно утверждать, что оно является простым с вероятностью большей, чем . Эта вероятность очень близка к единице,
однако всё же оставляет некоторую тень сомнения на простоте числа . В дальнейшем в этом пункте мы будем
считать, что заданное число является простым, а
нам требуется лишь доказать это.
В настоящее время известны детерминированные
алгоритмы различной сложности для доказательства простоты чисел. Мы
остановимся подробнее на одном из них, предложенном в 1983 г. в совместной
работе Адлемана. Померанца и Рамели. Для доказательства простоты или непростоты
числа этот алгоритм требует
арифметических операций. Здесь
— некоторая положительная абсолютная
постоянная. Функция хоть и медленно, но всё же
возрастает с ростом , поэтому алгоритм не является
полиномиальным. Но всё же его практические реализации позволяют достаточно
быстро тестировать числа на простоту. Существенные усовершенствования и
упрощения в первоначальный вариант алгоритма были внесены в работах X. Ленстры и А. Коена. Мы
будем называть описываемый ниже алгоритм алгоритмом Адлемана — Ленстры.
В основе алгоритма лежит использование сравнений
типа малой теоремы Ферма, но в кольцах целых чисел круговых полей, т. е.
полей. порождённых над полем числами
— корнями из 1. Пусть
— простое нечётное число и
— первообразный корень по модулю
, т. е. образующий элемент
мультипликативной группы поля , которая пиклична. Для
каждого целого числа , не делящегося на
, можно определить его индекс,
, называемый также дискретным
логарифмом, с помощью сравнения . Рассмотрим далее два
простых числа ,
с
условием, что делится на
, но не делится на
.
Следующая функция, определённая на множестве
целых чисел.
является
характером по модулю и порядок этого характера равен
.
Сумма
называется суммой Гаусса. Формулируемая ниже теорема 3
представляет собой аналог малой теоремы Ферма, используемый в алгоритме
Адлемана — Ленстры.
Теорема 3. Пусть —
нечетное простое число, . Тогда в кольце
выполняется сравнение
.
Если при каких-либо числах сравнение из теоремы 3 нарушается. можно
утверждать, что составное число. В противном
случае, если сравнение выполняется, оно даёт некоторую информацию о возможных
простых делителях числа . Собрав такую
информацию для различных , в конце концов
удаётся установить, что имеет лишь один
простой делитель и является простым.
В случае легко
проверить, что сравнение из теоремы 3 равносильно хорошо известному в
элементарной теории чисел сравнению

где — так называемый символ Якоби.
Хорошо известно также, что последнее сравнение выполняется не только для
простых , но и для любых целых
, взаимно простых с
. Заметим также, что для вычисления
символа Якоби существует быстрый алгоритм, основанный на законе взаимности
Гаусса и. в некотором смысле, подобный алгоритму Евклида вычисления
наибольшего общего делителя. Следующий пример показывает. каким образом
выполнимость нескольких сравнений типа (13) даёт некоторую информацию о
возможных простых делителях числа .
Пример (X. Ленстра). Пусть —
натуральное число, . для которого выполнены
сравнения

а кроме того с некоторым целым числом имеем
. (15)
Как уже указывалось, при простом сравнения (14) выполняются для любого
, взаимно простого с
, а сравнение (15) означает, что
есть первообразный корень по модулю
. Количество первообразных корней равно
, т. е. достаточно велико. Таким образом,
число с условием (15) при простом
может быть найдено достаточно быстро с
помощью случайного выбора и последующей проверки (15).
Докажем, что из выполнимости (14-15) следует, что
каждый делитель числа
удовлетворяет
одному из сравнений
или
. (16)
Не уменьшая общности, можно считать, что —
простое число. Введем теперь обозначения , где
и
—
нечётные числа. Из (15) и сравнения следует, что
. Далее, согласно (14). выполняются
следующие сравнения

означающие (в силу того, что символ Якоби может равняться лишь -1
или +1), что

При это равенство означает, что

, и, следовательно,
. Если же
, то
имеем 
. Этим
(16) доказано.
Информация такого рода получается и в случае
произвольных простых чисел и
с указанными выше свойствами.
Опишем схему алгоритма Адлемана — Ленстры для проверки
простоты :
1) выбираются различные простые числа и различные простые нечётные
такие, что
1) для каждого все
простые делители числа содержатся
среди и
не
делятся на квадрат простого числа;
1) .
2) для каждой пары
выбранных чисел ,
проводятся
тесты, подобные сравнению из теоремы 3. Если не
удовлетворяет какому-либо из
этих тестов — оно составное. В противном случае
3) определяется не
очень большое множество чисел, с которыми только и могут быть сравнимы простые
делители . А именно, каждый простой делитель
числа
должен
удовлетворять сравнению вида
,
.
4) проверяется, содержит ли найденное множество делители . Если при этом делители не обнаружены,
утверждается, что — простое
число.
Если число составное,
оно обязательно имеет простой делитель ,
меньший , который сам содержится среди возможных
остатков. Именно на этом свойстве основано применение пункта 4) алгоритма.
Сумма Якоби
определяется для двух характеров модулю
. Если характеры имеют порядок
, то соответствующая сумма Якоби
принадлежит кольцу . Поскольку числа
, участвующие в алгоритме, сравнительно
невелики, то вычисления с суммами Якоби производятся в полях существенно
меньшей степени, чем вычисления с суммами Гаусса. Это главная причина, по
которой суммы Якоби предпочтительнее для вычислений. При выполняется классическое соотношение
связывающее суммы Гаусса с суммами Якоби и позволяющее переписать
сравнение теоремы 3 в терминах сумм Якоби. Так. при и
соответствующее сравнение, справедливое
для простых , отличных от 2,3,7, принимает вид
,
где и
—
некоторый корень кубический из 1.
В 1984 г. было внесено существенное усовершенствование в алгоритм,
позволившее освободиться от требования неделимости чисел на квадраты простых чисел. В результате,
например, выбрав число и взяв
равным произведению простых чисел
с условием, что
делится
на , получим
, что
позволяет доказывать простоту чисел , записываемых сотней
десятичных знаков. При этом вычисления будут проводиться в полях, порождённых
корнями из 1 степеней 16, 9, 5 и 7.
Персональный компьютер с процессором Pentium-150. пользуясь
реализацией этого алгоритма на языке UBASIC, доказал простоту записываемого 65 десятичными
знаками, большего из простых чисел в примере Ривеста, Шамира и Адлемана за 8
секунд. Сравнение этих 8 секунд и 17 лет, потребовавшихся для разложения на
множители предложенного в примере числа, конечно, впечатляет.
Отметим, что опенка сложности этого алгоритма
представляет собой трудную задачу аналитической теории чисел. Как уже
указывалось, количество операций оценивается величиной .
Однако соответствующие числа и
, возникающие в процессе доказательства,
не могут быть явно указаны в зависимости от .
Доказано лишь существование чисел и
, для которых достигается оценка. Впрочем,
есть вероятностный вариант алгоритма, доказывающий простоту простого числа с вероятностью большей
за
арифметических
операций. А в предположении расширенной гипотезы Римана эта опенка сложности может
быть получена при эффективно указанных и
.
4. ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ АЛГОРИТМА
Представленный
выше алгоритм шифрования был реализован с помощью интегрированного пакета фирмы
Borland Delphi 5.0. Выбор данного языка программирования обоснован тем что,
он предоставляет такие возможности, как объектно-ориентированный подход к
программированию, основанный на формах, интеграция с программированием для Windows и компонентная технология. Среду
визуального программирования Delphi 5 позволяет с помощью компонентного подхода к созданию приложений,
быстро и качественно «собрать» интерфейс программы и большую часть
времени использовать именно на реализацию составленного алгоритма.
Программа
построена по технологии клиент/сервер, т.е. клиент передает по сети данные из
стандартного потока ввода (с клавиатуры), предварительно зашифровав, сервер,
получая поток данных, автоматически его расшифровывает.
Программный
продукт состоит из двух приложений. Первое приложение представляет собой
программу генерации ключей. Она выводит все простые числа заданного диапазона,
из которых потом выбираются числа и
. Там же находятся открытый и закрытый
ключи, которые сохраняются на диске. Второе приложение, основная программа,
производит соединение между двумя компьютерами и, отправляя сообщение, шифрует
его. Это приложение клиент. Приложение сервер получает сообщение и
расшифровывает его. Так же во второй программе содержится небольшая база данных
абонентов, хранящая в себе имена абонентов, IP адреса и их открытые ключи.
4.1. Реализованные алгоритмы
В
программном продукте были реализованы основные алгоритмы схемы RSA. Функция ModDegree
производит вычисление . Функция Prost находит все
простые числа заданного диапазона. Функция Evklid реализует алгоритм Евклида и
находит закрытый ключ . Функция HOD производит
вычисление наибольшего общего делителя и находит открытый ключ . Вышеперечисленные функции представлены в
приложении 1.
4.2. Анализ результатов
Результатом
работы созданной программы являются зашифрованные и расшифрованные сообщения.
Для тестирования
программы использовался пример приведенный в [11] ,
,
и
. Также
и
.
5. ВЫВОДЫ
Перейдем к
обсуждению выводов после детального просмотра специфики метода, реализованного
программного продукта на основе построенного алгоритма, а также представленного
анализа результатов по обработанному материалу.
5.1 Алгоритм
Использованный
алгоритм RSA имеет ряд преимуществ:
1) алгоритм RSA является ассиметричным, т.е. он
основывается на распространении открытых ключей в сети. Это позволяет
нескольким пользователям обмениваться информацией, посылаемой по незащищенным
каналам связи;
2) пользователь
сам может менять как числа ,
, так и открытый и закрытый ключ по своему
усмотрению, только потом он должен распространить открытый ключ в сети. Это
позволяет добиваться пользователю нужной ему криптостойкости.
При всех этих
преимуществах данный алгоритм имеет существенный недостаток – невысокая
скорость работы. Алгоритм RSA
работает более чем в тысячу раз медленнее симметричного алгоритма DES.
Из всего
вышесказанного можно заключить, что данный алгоритм шифрования, хотя довольно
медленный, но он ассиметричный и позволяет добиваться нужной криптостойкости,
что делает его незаменимым при работе в незащищенных каналах связи.
5.2 Алгоритм и программа
Исходя из
проработанных данных, по построенному алгоритму и созданному программному
продукту сделаны следующие выводы:
1) построенный
алгоритм, а соответственно и созданный на его базе программный продукт,
полностью реализует базовые механизмы схемы RSA и, таким образом удовлетворяют основным поставленным задачам;
2) данный
программный продукт построен по технологии клиент/сервер и предназначен
сохранять конфиденциальность передачи информации в сети.
Таким образом, по
выводам о построенном алгоритме и созданном программном продукте можно
заключить, что он подходит для решения проблем шифрования информации, связанных
с передачей данных по сети.
ЗАКЛЮЧЕНИЕ
В рамках данного дипломного проектирования перед
студентом Малышевым А.А. была поставлена задача: на основе алгоритма RSA для шифрования блоков данных, построить алгоритм и реализовать
программный продукт для шифрования потоков данных.
В результате выполнения дипломного проектирования
был составлен принципиальный алгоритм для решения поставленной задачи. Далее он
был детализован и реализован на ЭВМ. В конце, был проведён анализ полученных
результатов, и сделаны необходимые выводы.
За основу построения алгоритма был принят алгоритм RSA для шифрования блоков данных, изучена соответствующая литература по
алгоритму, и был построен алгоритм и реализован программный продукт в среде
визуального программирования Delphi 5 под ОС типа Windows
для IBM PC-совместимых компьютеров.
Созданный
программный продукт позволяет решить поставленную задачу и, дополнительно,
содержит в себе небольшую базу данных абонентов. Т.е. в результате выполнения
программы исходное сообщение шифруется и передается по сети, где оно
расшифровывается. Также можно указать о том, что программа имеет интуитивно
понятный интерфейс, что дополнительно помогает пользователю с наибольшей
результативностью использовать всю ресурсную базу.
В заключении,
после анализа полученных результатов были сделаны выводы, согласно которым
алгоритм работает и применим для поставленной задачи.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Ященко В. В. Основные понятия криптографии // Математическое
просвещение. Сер. 3. №2. 1998. С. 53-70.
2. Виноградов И.
М. Основы теории чисел. М.: Наука. 1972.
3. Карацуба А. А. Основы аналитической теории чисел. М.: Наука.
1983 г.
4. Кнут Д. Искусство программирования на ЭВМ. Т.2: Получисленные
алгоритмы. М.: Мир. 1977.
5. Ахо А.. Хопкрофт Дж.. Ульман Дж. Построение и анализ вычислительных
алгоритмов. М.: Мир. 1979.
6. Варновский Н. П. Криптография и теория сложности // Математическое
просвещение. Сер. 3. №2. 1998. С. 71-86.
7. Василенко О. Н. Современные способы проверки простоты чисел //
Кибернетический сборник, вып. 25. 1988. С. 162-188.
8. Прахар К. Распределение
простых чисел. М.: Мир. 1967.
9.Боревич З.И.
Шафаревич И.Р. Теория чисел. М.: Наука. 1964.
10. Кострикин
А.И. Введение в алгебру. М.: Наука. 1977.
11. Брассар Дж. Современная
криптология. Мир ПК. №3. 1997.
ПРИЛОЖЕНИЕ
1
Листинг программы
Модуль Key.pas
Function
Prost(n:integer):Boolean;
var k:Boolean;
i:integer;
begin
k:=true;
if n<>2 then
for i:=2 to
trunc(sqrt(n))+1 do
if (n/i)=trunc(n/i)
then
begin
k:=False;
Break;
end;
Prost:=k;
end;
{________________________________________________________}
Function
Evklid(Num1,Num2:integer):integer;
var r,q1,p1:array of
integer;
i,n,k:integer;
begin
if Num1>=Num2 then
begin
SetLength(r,10);
r[0]:=Num1;
r[1]:=Num2;
end
else
begin
SetLength(r,10);
r[0]:=Num2;
r[1]:=Num1;
end;
i:=1;
while r[i]<>0 do
begin
inc(i);
r[i]:=r[i-2] mod
r[i-1];
end;
n:=i-2;
SetLength(q1,n+1);
for i:=0 to n do
q1[i]:=r[i] div r[i+1];
SetLength(p1,n+2);
p1[0]:=1;
p1[1]:=q1[0];
k:=length(q1);
if k>1 then
for i:=2 to k do
p1[i]:=q1[i-1]*p1[i-1]+p1[i-2];
Result:=trunc(power(-1,k-1))*p1[k-1]
mod Num2;
end;
{________________________________________________________}
Function
HOD(Num1,Num2:integer):integer;
var r:array of integer;
i:integer;
begin
if Num1>=Num2 then
begin
SetLength(r,Num2);
r[0]:=Num1;
r[1]:=Num2;
end
else
begin
SetLength(r,Num1);
r[0]:=Num2;
r[1]:=Num1;
end;
i:=1;
While r[i]<>0 do
begin
inc(i);
r[i]:=r[i-2] mod r[i-1];
end;
Result:=r[i-1];
end;
{________________________________________________________}
Function
ModDegree(Num,Degree,n:integer):integer;
var x:array of integer;
i:integer;
begin
SetLength(x,n);
x[1]:=Num mod n;
for i:=2 to Degree do
x[i]:=x[i-1]*Num mod n;
Result:=x[Degree];
end;
ПРИЛОЖЕНИЕ 2
Главная форма программы
ПРИЛОЖЕНИЕ 3
Форма базы данных абонентов
ПРИЛОЖЕНИЕ 4
Форма нахождения простых чисел и генерации ключей
Системы с открытым ключом: алгоритм шифрования RSA
Нижегородский
государственный университет им. Н. И. Лобачевского
Факультет
вычислительной математики и кибернетики
Кафедра
информатизации и автоматизации научных исследований
Курсовая
работа
Системы с
открытым ключом: алгоритм шифрования RSA
Выполнил: Скульский М. А.
Научный руководитель: Фомина И. А.
Н. Новгород,
1997 г.
Оглавление
Введение
Понятие криптосистемы с открытым
ключом
Описание алгоритма RSA
Возможные атаки на RSA
Практическая реализация RSA
Обоснование алгоритма
Комментарии к программе
Текст программы
Литература
Введение
Основной целью построения криптографических
систем всегда была защита информации при ее передаче и хранении. Эта проблема
остается актуальной и до сегодняшнего дня, однако же развитие вычислительных систем
придало ей новое качество: вопрос уже не просто в том, чтобы, скажем, Александр
мог послать письмо Борису, не опасаясь, что оно будет прочитано Сергеем.
Сетевые компьютерные системы могут включать в себя сотни и даже тысячи
пользователей; в такой ситуации классическая симметричная схема оказывается
неэффективной. Новым требованием к криптосистемам также является обеспечение
аутентификации сообщения — доказательство того, что Борис получил именно то
сообщение, которое ему отправил Александр, и что оно не было подделано или
изменено злоумышленником в процессе передачи. Кроме того, приходится мириться с
тем, что к зашифрованной информации потенциально может иметь доступ довольно
большое количество людей — например, маршрут любого сообщения, проходящего через
Internet, в принципе невозможно предсказать, оно может пройти через несколько
десятков узлов прежде чем попадет к своему адресату. Так что, если прежде
наиболее надежным подходом к защите информации был все-таки амбарный замок, то
теперь задача все более усложняется противоречивыми требованиями одновременно
надежности и секретности передачи и легкости доступа к информации.
Традиционная криптографическая схема выглядит
следующим образом. Александр и Борис оба знают некий ключ, с помощью которого
они могут обмениваться зашифрованными сообщениями так, что любое третье лицо,
даже если ему удастся перехватить шифровку, не сможет ничего в ней понять.
Такая схема называется симметричной, так как и адресат, и отправитель
используют один и тот же ключ для шифрования и дешифрования. Давайте попробуем
применить ее к какой-нибудь простой распределенной задаче. Пусть у нас есть
некое сетевое устройство — например, ядерная ракетная установка, — принимающая
команды по сети. Конечно, не от всех, а только от имеющих соответствующие права
доступа. Пусть у нашего устройства есть некий ключ, которым должны быть
зашифрованы все команды, подаваемые на него. Этот ключ, так как систему мы
предполагаем симметричной, необходимо сообщить всем пользователям. Теперь
предположим, что Александр зашифровал сообщение “Стреляй в Бориса” и отправил
его нашему устройству. Другой пользователь, Сергей, подкупленный Борисом,
перехватил это сообщение и, зная ключ, с легкостью расшифровал его, сообщив о
содержании Борису. Казалось бы, проблема легко решается введением разных
паролей для разных пользователей. Ну а если доступ к данному устройству должен
быть более или менее свободным?
Теперь давайте представим себе сеть из,
например, ста пользователей и сервера баз данных. Между пользователями и сервером
происходит некий обмен информацией, причем всем пользователям совершенно
необязательно и, более того, нежелательно знать информацию, хранимую и
запрашиваемую на сервере другими пользователями. Разумеется, необходимо
защитить сам сервер — так, чтобы каждый пользователь имел доступ только к своей
информации. Но ведь все это происходит в одной сети, и все данные передаются по
одним и тем же проводам, а если это, скажем, что-нибудь типа Token Ring, то
информация от сервера до владельца последовательно проходит через все станции,
находящиеся между ними в кольце. Следовательно, ее необходимо шифровать. Можно
опять ввести для каждого пользователя свой пароль, которым и шифровать весь
информационный обмен с сервером. Но как отличить одного пользователя от другого?
Один вариант — перед началом работы спрашивать у пользователя этот самый пароль
и сверять с хранящимся на сервере. Но тогда он с легкостью может быть
перехвачен в том же самом канале связи. Другой вариант — пароль не спрашивать,
а верить тому, что пользователь говорит о себе. Так как пароль секретный, то
даже сказав серверу “Я — Александр!”, злоумышленник не сможет расшифровать
получаемые данные. Но зато он сможет получить столько материала для взлома
шифра, сколько ему захочется — при этом часто можно предсказать ответ сервера
на какой-то специфический вопрос и получить сразу шифр и соответствующий
оригинальный текст. Согласитесь, это очень продвигает нас в взломе сервера.
Данная проблема носит название проблемы
распределения ключей. Ее наличие делает симметричную схему неприспособленной
для задач обмена данными с большим количеством пользователей, так как в ней для
шифрования и дешифрования используется один и тот же ключ.
Понятие
криптосистемы с открытым ключом
Концепция криптосистем с открытым ключом была
предложена в 1976 г Уайтфилдом Диффи и Мартином Хеллманом в качестве решения
проблемы распределения ключей. В соответствии с ней, каждая сторона получает
пару ключей — открытый и закрытый. Открытый ключ распространяется свободно, в
то время как закрытый держится в тайне. Исходный текст шифруется открытым
ключом адресата и передается ему. Обратный процесс в принципе не может быть
выполнен с помощью открытого ключа, для расшифровки получатель использует
закрытый ключ, который известен только ему. Таким образом, кто угодно может
посылать шифрованные сообщения, для этого ему не надо знать ничего тайного, но
при этом только владелец закрытого ключа сможет их прочитать.
Системы с открытым ключом базируются на
использовании так называемых односторонних функций — функций, вычислить
значения которых во много раз проще, чем значения их обратной функции. Особенно
важен подкласс односторонних функций-ловушек — так называются односторонние
функции, вычисление которых в обратную сторону возможно при наличии некоторой
дополнительной информации, и очень трудно иначе. Открытый ключ является
параметром при вычислении односторонней функции; закрытый же представляет
информацию, необходимую для вычисления обратной. Хорошая односторонняя функция
должна обладать следующими очевидными свойствами:
Обратную функцию очень сложно вычислить, не зная
закрытого ключа;
Закрытый ключ невозможно найти из открытого;
Сложность вычисления должна катастрофически
возрастать с возрастанием длины ключа.
Существует большое количество функций, которые
считаются односторонними, однако отсутствие полиномиального решающего алгоритма
ни для одной не доказана. Поэтому при использовании любой системы с открытым
ключом всегда остается риск того что в будущем обнаружится быстрый алгоритм
нахождения обратной функции без закрытого ключа. На самом деле, корнем любой
такой функции является какая-нибудь математическая проблема, традиционно
считающаяся трудной. Если удается доказать, что раскрытие шифра эквивалентно
разрешение этой проблемы, то проблема надежности шифра зависит от
справедливости гипотезы P ¹
NP. Наиболее часто
используются:
Разложение больших чисел на простые множители —
RSA;
Вычисление дискретного логарифма (логарифма в
конечном поле) — система Эль-Гамаля;
Вычисление квадратных корней в конечном поле —
система Рабина;
Вычисление дискретного логарифма над
эллиптическими кривыми;
Задача о камнях;
Таким образом, с развитием криптографии все
более размывается граница между ней и другими областями математики. Новейшие
достижения в решении сложных математических проблем сразу же находят применения
в криптографии и наоборот, наличие такого лакомого куска подвигает многих
математиков на исследования в смежных областях.
Описание алгоритма
RSA
Выберем достаточно большие простые числа p и q;
Вычислим n=pq, называемый модулем;
Выберем e<n взаимно простое с j=(p-1)(q-1);
е называется открытой экспонентой;
Найдем d | res(p-1)(q-1)(ed)=1 (то есть, ed=1
mod ); d называется закрытой экспонентой;
Теперь (n, d) — закрытый ключ; (n, e) — открытый
ключ;
Шифрование: ;
Дешифрование:
Здесь m — целое число, .
Ниже я сделаю некоторые комментарии
к сказанному, а также приведу полное обоснование данного алгоритма, а сейчас
обсудим вопрос о его потенциальной криптостойкости.
Возможные атаки на
RSA
Главным и наиболее очевидным способом сломать
RSA является отыскание закрытого ключа по данному открытому. Это позволило бы
злоумышленнику читать все сообщения, зашифрованные этим ключом. Сделать это
можно, например, разложив n на простые множители p и q. После этого отыскание d
является тривиальной задачей. Надежность RSA основывается на трудности
разложения n.
Лучшим алгоритмом, применяемым для факторизации
на сегодняшний день, является NFS (Number Field Sieve — числовое решето),
вычислительная сложность которого оценивается как O(exp(1.9223(ln n)1/3 (ln ln
n)2/3)). Алгоритм этот сравнительно новый — при разложении знаменитого числа
RSA-129, полученного в марте 1994, еще использовалось менее эффективное
квадратичное решето, а не NFS. RSA-129 — это 129-значное число, разложение
которого считалось весьма желательным с 1977 года. Для осуществления этого
проекта через Internet было задействовано 1600 компьютеров (в том числе два
факса), работавших в течение восьми месяцев. По некоторым оценкам использование
NFS могло бы сократить этот срок в три-четыре раза. Таким образом, если 130 знаков
примерно составляют предел для квадратичного решета, то использование NFS
поднимает планку до 140-150 знаков. Модуль длиной 512 бит содержит около 155
знаков, поэтому для практически большинства приложений этого достаточно. По
мнению фирмы RSA Data Security разложение такого числа будет стоить порядка
$1,000,000 и займет около восьми месяцев. Также по ее мнению ключ длиной 768
бит останется неразложимым примерно до 2004 года.
Другим способом сломать RSA является
отыскание способа вычисления корней степени e по модулю n. Так как , то
даст нам
исходное сообщение m. Этот способ не является эквивалентным разложению n, так
как он не дает нам закрытого ключа d. Тем не менее само по себе вычисление
корней над полями Галуа представляет собой сложную задачу. Известна теорема
Рабина о том, что вычисление эквивалентно факторизации n, так что
на самом деле практически не предпринималось попыток раскрытия шифра в этом
направлении.
Все прочие способы не дают
возможности раскрытия всех сообщений, зашифрованных данным ключом. Однако
существуют подходы, иногда дающие возможность взломать данное конкретное
сообщение. Простейший из них — угадывание оригинала. Злоумышленник видит шифр,
догадывается, что в сообщении написано “Стреляй в Бориса”, зашифровывает свою
версию известным открытым ключом и сравнивает с шифровкой. Еще один подход
основан на свойствах преобразования RSA. Если одно и то же сообщение посылается
e разным получателям (где е не основание натурального логарифма, а открытая
экспонента), то злоумышленник, перехвативший все е шифровок, сможет
восстановить исходное сообщение.
Практическая
реализация RSA
Практическая реализация RSA сопряжена с
определенными проблемами. Первая и, пожалуй, главная из них — вычислительная
сложность алгоритма. По сравнению с большинством симметричных криптосистем RSA
работает в несколько сот раз медленнее. При обычной реализации генерация ключа
длины k требует O(k4) операций; шифрование — O(k2), а расшифровывание- O(k3)
операций. Наиболее быстрая из чисто программных реализаций (bSafe 3.0, RSA Data
Security) осуществляет шифрование со скоростью 21.6 Kбит/сек для 512-битного
ключа. Это очень быстро если представить себе операции с числами из 150 знаков,
но само по себе это конечно же медленно. Поэтому обыкновенно системы с открытым
ключом используют в сочетании с какой-нибудь симметричной системой — например,
DES. Допустим, Александр хочет послать Борису сообщение. Для этого он
генерирует случайный ключ DES и шифрует им текст сообщения. После этого он
берет открытый ключ Бориса и шифрует им ключ DES. То, что получается в
результате, носит название “двоичного конверта”(digital envelope) и сочетает в
себе лучшее из обоих принципов — скорость симметричных систем и удобство
использования систем с открытым ключом. Двоичный конверт можно безопасно
передавать по линиям связи — используя свой закрытый ключ, Борис сначала
восстановит ключ DES, а соответственно и текст исходного сообщения.
Обычной практикой является выбор не слишком
большого e — это не отражается на криптостойкости алгоритма, но существенно
ускоряет шифрование. Тем не менее, d почти всегда оказывается велико. Поэтому
возводить при дешифровании cd обычно оказывается не самой лучшей идеей. К
счастью, использование Китайской теоремы об остатках позволяет существенно
понизить порядок возведения в степень, а также свести вычисления по модулю n к
вычислениям по модулю p и q. Подробнее об этом см. у Е. Бубновой [2].
Результаты несложного теста, проведенного нами с помощью нашей (весьма
медленной) реализации RSA приведены в таблице и позволяют наглядно увидеть,
почему надо пользоваться Китайской теоремой об остатках и не надо ничего
возводить в степень “в лоб”.
|
Размер |
Время |
Время |
|
256 |
12 |
5 |
При шифровании мы использовали метод
последовательного возведения в квадрат, а при дешифровании — теорему об
остатках. В результате шифрование оказалось примерно в 2.5 раза медленнее
дешифрования!! То есть, грубо говоря, возведение в степень 30-40 занимает втрое
больше времени, чем в степень 1,000,000,000.
Еще одна сложная проблема, связанная с
реализацией алгоритма — это генерация p и q. Самый примитивный вариант — решето
Эратосфена — хорошо работает для чисел длиной знаков 10, не более. Для
генерации пригодного к использованию ключа в 150 знаков этот метод не работает.
Фирма RSA Data Security рекомендует использовать вероятностный подход — то
есть, генерировать не на самом деле простые числа, а те, для которых
вероятность того, что они составные, меньше наперед заданной малой величины.
Существуют хорошие алгоритмы, позволяющие доказать это для заданного числа —
или показать, что оно составное. Однако если тестируемое число на самом деле
окажется составным, криптостойкость RSA падает. Поэтому альтернативой этому
является использование намного более медленных тестов, позволяющих абсолютно
точно сказать простое это число или составное. Классическая группа таких тестов
основана на знании простых множителей для p-1 или p+1; если их можно найти, то
появляется возможность доказать или опровергнуть простоту p. Вообще проблема
доказательства простоты достаточно сложна, но совершенно не эквивалентна
разложению чисел на множители, так что за приемлемое время всегда можно найти
нужные p и q.
Обоснование
алгоритма
Сначала выведем некоторые важные свойства
остатков. Через a=resnx будем обозначать остаток от деления n на x;
эквивалентная этому запись x=a mod n. Все числа считаются целыми и
неотрицательными.
Свойства остатков
Пусть x = a mod n; y = b mod n; Тогда resnxy =
resnab
x=un+a; y=vn+b;
Следовательно,
xy=(un+a)(vn+b)=uvn2+avn+bun+ab;
resnxy=resnab
Пусть x = a mod
n; y = b mod n; Тогда
resn(x+y) = resn(a+b)
Пусть x = a mod
n; Тогда
resn(xm) = resn(am)
= resn(x*x*…*x) = resn(a*a*…*a) =
resn(am)
Пусть x<n. Тогда resnx=x (resn(x))
= resnx
Пусть n=pq; Тогда resp(resnx) =
respx
Следующие два утверждения приводятся
без доказательства.
Теорема Эйлера
Пусть p — простое, a<p. Тогда , где
— к-во
чисел < n и вз. простых с n; криптосистема
открытый ключ
Лемма
Если n = pq, p и q простые, то
Функция называется
функцией Эйлера. Следующая теорема использует эти результаты для доказательства
возможности найти d; ее доказательство представляет практический способ его
нахождения.
Теорема
Пусть e взаимно просто с . Тогда
уравнение имеет
единственное решение u <
Существование.
Так как НОД(e, )=1, то
Возможны два случая:>0, v<0.
Тогда ue=1+(-v);
Следовательно ue = 1 mod <0,
v>0.
Рассмотрим
Пусть u >, тогда
Единственность
Пусть
Следовательно,
Отсюда окончательно имеем
Наконец, последняя теорема
доказывает корректность самого алгоритма.
Теорема
При соответствующем условиям
алгоритма выборе e и d,
Обозначим это выражение за (*).
Если m взаимно просто с n, то по
теореме Эйлера что и
требовалось. В противном случае либо m=tp, либо m=tq, так как у n нет других
делителей; без ограничения общности будем предполагать m=tp. При этом t
необходимо меньше q, так как m<n=pq
.
Но (т. Эйлера); следовательно, это
равно
(+)
Найдем r. Выражение (+) на самом
деле означает, что t*p*…*p = Apq+r. Так как это равенство в целых числах, то
отсюда следует, что r делится на p. То есть, t*p*…*p=Aq+r/p=r1;
Теперь т.к. по
т.Эйлера .
Следовательно, (*)=r=tp=m и в этом
случае.
Комментарии к
программе
В качестве иллюстрации предлагается реализация
алгоритма RSA с длиной модуля 32 бита. В программе используются настоящие
простые числа, генерируемые с помощью решета Эратосфена. Для возведения в
степень при шифровании используется последовательное возведение в квадрат; при
дешифровании — Китайская теорема об остатках. В программе реализован аппарат
длинной 64-битной арифметики.
Текст программы
#include <dos.h>
#include <stdio.h>
#include <iostream.h>
#include <string.h>
#include «compcl.cpp»
/*************************************/
/** The following global variables **/
/** are required for all encryption **/
/** and decryption operations. **/
/*************************************/
/* The modulus */long modulus=0;
/* The primes; n=pq */int prime1=0, prime2=0;
/* The public exponent */int pub_exp=0;
/* The private exponent */long priv_exp;
/* The Euler Phi = (p-1)(q-1) */
unsigned long phi=0;
#include «math.cpp»
/*************************************/
/** RSA functions follow. **/
/*************************************/
/* Generate the keys for the first
time*/
void InitRSA(void);
/* Initialize RSA for encryption
*/InitRSAe(unsigned int apub_exp, unsigned long amodulus);
/* Initialize RSA for decryption */InitRSAd
(unsigned int aprime1, unsigned int aprime2, comp apriv_exp);
/* Encrypt one LONG of data */
unsigned long encrypt (unsigned long data);
/* Decrypt one LONG of ciphertext */
unsigned long decrypt (unsigned long cipher);
/*************************************/
/** Hehe — the actual function **/
/** instances follow **/
/*************************************/InitRSA(void)
{
get_primes(&prime1,&prime2);
modulus=((unsigned long)prime1)*((unsigned
long)prime2);
phi=((unsigned long)(prime1-1))*((unsigned
long)(prime2-1));
get_exponents(&pub_exp, &priv_exp);
}
void InitRSAe(unsigned int apub_exp,
unsigned long amodulus)
{
modulus=amodulus; pub_exp=apub_exp;
}
void InitRSAd (unsigned int aprime1,
unsigned int aprime2, unsigned long apriv_exp)
{
prime1=aprime1; prime2=aprime2;
phi=((unsigned long)prime1-1)*((unsigned
long)prime2-1);
modulus=(unsigned long)prime1*(unsigned
long)prime2;
priv_exp=apriv_exp;
}
#include
«encr.cpp»ErrCommand(char *Msg)
{
cout << «Error: «;
cout << Msg;
cout << «n»;
exit(1);
}
/************************************************************/
/************************** M A I N
*************************/
/****************888***********************888***************/main()
{
char name[128];
FILE *f, *fi, *fo;
time_t st=time(NULL);int i, j;
unsigned long l;
cout << «nRSA
implementation (c) 1997 M.Skulsky & K.Bubnova.n»;
cout << «Special thanks to Rivest, Shamir,
Aldeman for their invaluable help, ton»;
cout << «Euclid, Euler, Fermat and
Galois for having provided a bunch of very usefuln»;
cout << «theorems and to V.N.
Shevchenko for having made us able to understand them.nn»;
switch (_argc) {
case 4:
case 2:
case 1:
cout << «Usage: rsa -k
<key file name>n»;<< » — for generating random
keysn»;<< » rsa -e <plain file> <encrypted file>
<public key file>n»;
cout << » — for encryptionn»;
cout << » rsa -d
<encrypted file> <plain file> <private key file>n»;<<
» — for decryptionnn»;<< «Public and private key files
have .PBK and PVK respectively, so these are n»;<< «added to
the <key file name> that you specify.n»;
exit(0);
case 3:
if
(strcmp(strlwr(_argv[1]),»-k»)) ErrCommand(«Command not
recognized.n»);();(name, _argv[2]);(name, «.pbk»);=fopen(name,
«wb»);(f==NULL) ErrCommand(«Invalid path.»);(&modulus,
sizeof(modulus), 1, f);(&pub_exp, sizeof(pub_exp), 1, f);(f);(name,
_argv[2]);(name, «.pvk»);=fopen(name, «wb»);(&prime1,
sizeof(prime1), 1, f);(&prime2, sizeof(prime2), 1, f);(&priv_exp,
sizeof(priv_exp), 1, f);(f);<< «Private and public keys successfully
created.n»;
break;5:
if
(!strcmp(strlwr(_argv[1]),»-e»)) { /* encrypting */
f=fopen (_argv[4], «rb»);
if (f==NULL) ErrCommand («Can’t
open public key!»);
fread (&l, sizeof(l), 1, f);
fread (&i, sizeof(i), 1, f);
fclose(f);
InitRSAe (i, l);((fi =
fopen(_argv[2], «rb»))==NULL)
ErrCommand («Can’t open plaintext
file!»);
if ((fo = fopen(_argv[3],
«wb»))==NULL)
ErrCommand («Can’t create ciphertext
file!»);=0;
while (!feof(fi)) {
l=0;
i=fread (&l, 1, 3, fi);
if (i==0) break;
l=encrypt(l);
fwrite (&l, 1, sizeof (long), fo);
if (j++==50) {j=0; cout << «+»;
}
} /* while */
printf («n»);
fclose (fi);
fclose (fo);
printf («Successfully encrypted
%sn», _argv[2]);
break;
}if
(!strcmp(strlwr(_argv[1]),»-d»)) { /* decrypting */
f=fopen (_argv[4], «rb»);
if (f==NULL) ErrCommand («Can’t
open private key!»);
fread (&i, sizeof(i), 1, f);
fread (&j, sizeof(j), 1, f);
fread (&l, sizeof(l), 1, f);
fclose(f);
InitRSAd (i, j, l);((fi =
fopen(_argv[2], «rb»))==NULL)
ErrCommand («Can’t open ciphertext
file!»);
if ((fo = fopen(_argv[3],
«wb»))==NULL)
ErrCommand («Can’t create plaintext
file!»);
j=0;
while (!feof(fi)) {
i=fread (&l, 1, sizeof (long), fi);
if (i==0) break;
if (i==sizeof(long)) {
l=decrypt(l);
fwrite (&l, 1, 3, fo);
}
else /* unexpected end of file encountered */
ErrCommand («Broken ciphertext!»);
if (j++==50) {j=0; cout <<«+»;}
} /* while */
printf («n»);(fi);
fclose (fo);
printf («Successfully decrypted
%sn», _argv[2]);
break;
} else ErrCommand(«Command not
recognized.n»);
}; /* switch */
st = time(NULL)-st;
printf («Time running: %lu
seconds.n», st);
}
/************************ ENCR.CPP
************************/
/************ This file contains the encryption
**************/
/*************** and decryption procedures
*******************/
/************************************************************/
unsigned long encrypt (unsigned long
data)
{
comp c, res, cmod;
int i;=modulus;
c=data;
c=(c*c)%cmod;
res=c;
for (i=1; i<pub_exp/2; i++)
res = (res*c)%cmod;=data;
res=(res*c)%cmod;
return res.lo();
}
unsigned long crt (unsigned long c,
unsigned int m);long decrypt (unsigned long cipher)
{
comp a, b, M, u, Cp, Cq, Bmp;= crt (cipher,
prime1);
b = crt (cipher, prime2);
u = inverse (prime2, prime1);=
(unsigned long) prime1;
Cq = (unsigned long) prime2;=
b%Cp;(a >= Bmp)
M=(((a-Bmp)*u)%Cp)*Cq+b;
else
M=(((a+Cp-Bmp)*u)%Cp)*Cq+b;M.lo();
}
unsigned long crt (unsigned long c,
unsigned int m)
{
unsigned long dmm;
unsigned int i;
unsigned long res=1, cmm;= c%m;
dmm = (unsigned long) (m-1);
dmm = priv_exp%dmm;(i=0; i<dmm; i++) {
res*=cmm%m;
if (res>=m) res %= m;
}res;
}
/***************************************
MATH.CPP *************************************/
#include <stdlib.h>
#include <mem.h>
#include <time.h>
/**************************************/
/************* Prototypes *************/
/**************************************/long
inverse(unsigned int x, unsigned long iModulus);get_primes(unsigned int *p1,
unsigned int *p2);get_exponents(unsigned int *pbe, unsigned long *pve);
/**************************************/
/********** Function bodies ***********/
/**************************************/
int iter;inv (unsigned int x,
unsigned long n, unsigned long *a, unsigned long *b)
{
unsigned long q, r, t;
q = n/x;
r = n%x;(r==1) { *b=q; *a=1; }
else {
inv(r, x, a, b);
iter++;= *a;
*a = *b;
*b = t+q*(*b);
}
}
unsigned long inverse (unsigned int
x, unsigned long n)
{
unsigned long a,b;=0;
inv (x, n, &a, &b);
if (iter%2==0) return n-b; else
return b;
}
unsigned long rnd(unsigned long
upto)
{
unsigned long t=time(NULL);=t*rand();
return t%upto;
}
#define MaxE 32767get_primes(unsigned int *p1,
unsigned int *p2)
{
char *c;
unsigned long i=1, j, k;=(char *)malloc(MaxE+1);
if (c==NULL) {
cout<<«Error: Out of memory!n»;
exit(1);
};
memset (c, 0, MaxE);
while (i<MaxE) {
for(j=3;(k=(j*(2*i+1)-1)/2)<MaxE;j+=2)
*(c+k)=1;
i++;
while ((i<MaxE) && *(c+i)) i++;
}
while (((i=rnd(MaxE))<MaxE/2) ||
*(c+i));
*p1=2*i+1;
j=i;
while (((i=rnd(MaxE))<MaxE/2) || *(c+i) ||
(i==j));
*p2=2*i+1;(c);
}
void get_exponents(unsigned int
*pbe, unsigned long *pve)
{
unsigned int n=random(10);{
n=random(10);
*pbe=n*n-n+41;
} while ((phi%*pbe)==0);
*pve=inverse(*pbe, phi);
}
/********************************* COMP.CPP
*********************************/comp
{
unsigned long a,b; /* a-high, b-lower */:
comp(unsigned long lo=0, unsigned long
hi=0);&operator =(comp c);
comp &operator =(unsigned long c);
comp operator +(comp c);
comp operator -(comp c);
comp operator *(comp c);
comp operator /(comp c);
comp operator %(comp c);
comp operator <<(int i);
int operator >(comp c);
int operator >=(comp c);
int operator ==(unsigned long l);
int operator ==(comp c);long lo(void);
unsigned long hi(void);
/*private:*/
void set1(int where);
int is1(int where);
int pow(void);
};
/**** Results of the last division
op ****/
comp lastdiv, lastmod;
comp::comp(unsigned long lo,
unsigned long hi)
{
a=hi;
b=lo;
}
comp &comp::operator =(comp c)
{
a=c.a; b=c.b;
return (*this);
}
comp &comp::operator =(unsigned
long c)
{
a=0; b=c;
return (*this);
}
comp comp::operator +(comp c)
{
comp res;
int i;
int was, is;
unsigned long l;
res=*this;=b&(1ul<<31);
for (i=0;i<=31;i++) {
res.b+=c.b & (1ul<<i);
is=(res.b & (1ul<<31))!=0;
if (was && !is) res.a++;
was=is;
}
res.a+=c.a;
return res;
}
comp comp::operator +(unsigned long
l)
{
comp t=l;*this+t;
}
comp comp::operator -(comp c)
{
comp res;
if (a<c.a || (a==c.a &&
b<c.b))
res=0;
else if (a>=c.a && b>=c.b) {
res.a=a-c.a;
res.b=b-c.b;
}
else {
res.b=(0xffffffff)-(c.b-b)+1;
res.a=a-c.a-1;
}
return res;
}
comp comp::operator *(comp c)
{
comp res=0;
int i, llen;=c.pow();
for(i=0;i<=llen;i++)
if (c.is1(i)) res=res+(*this<<i);res;
}
comp comp::operator /(comp t)
{
comp th, r, result=0, rt;
int s1, s2;=pow(); s2=t.pow();
if (s1<s2) {
lastdiv=0l;
lastmod=*this;
return 0;
}=*this;
while (s1>s2) {
r=0;
r.set1(s1-s2);
if(th>=(rt=r*t)) th=th-rt; else {r=0;
r.set1(s1-s2-1); th=th-r*t;}
result=result+r;
s1=th.pow();
}(s1==s2 && th>=t) {
result=result+1l;
th=th-t;
}=result;
lastmod=th;
return result;
}
comp comp::operator %(comp c)
{
*this/c;
return lastmod;
}
void comp::set1(int where)
{
unsigned long *l;(where>31) {
l=&a;
where-=32;
}
else l=&b;
*l=*l|(1l<<where);
}comp::pow(void)
{
int i,j;
unsigned long *l;(a==0) {
l=&b;
j=0;
}
else {
l=&a;
j=32;
}(*l==0) return 0;
for (i=31;!(*l>>i);i—);
return i+j;
}
comp comp::operator <<(int i)
{
comp t=*this;(;i>0;i—) {
t.a=(t.a)<<1;
if(t.b & (1ul<<31)) (t.a)++;
t.b=(t.b)<<1;
}t;
}
int comp::operator >(comp c)
{
comp t=*this-c;
return (t.a!=0) || (t.b!=0);
}
int comp::operator >=(comp c)
{
return (*this==c) || (*this>c);
}
int comp::is1(int where)
{
unsigned long *l;
unsigned long res;
if (where>31) {where-=32;
l=&a; }
else l=&b;
res = *l & (1ul<<(unsigned
long)where);
return res!=0;
}
int comp::operator ==(unsigned long
l)
{
return ((a==0) && (b==l));
}
int comp::operator ==(comp c)
{
return ((a==c.a) && (b==c.b));
}
unsigned long comp::lo(void)
{
return b;
}
unsigned long comp::hi(void)
{
return a;
}
Литература
1. Баричев
С., Криптография без секретов
2. Е.Бубнова,
Системы с открытым ключом: алгоритм дешифрования RSA
. RSA
Laboratories, Frequently Asked Questions About Today’s Cryptography, 1995
. Д.Сяо,
Д. Керр, С.Мэдник, Защита ЭВМ
. Л.Дж.Хоффман,
Современные методы защиты информации
. James
Nechvatal, Public key cryptography, 1991
. Chris
K.Caldwell, Finding Primes and proving primality
Содержание:
ВВЕДЕНИЕ
Информация (данные) в общем смысле – это сведения, представленные в различной форме, которая может быть распознана человеком и/или специальными устройствами. С течением времени понятие информации, используемое в повседневной речи, претерпело значительные изменения. Главным образом это произошло из-за распространения технологий, связанных с коммуникацией. В середине XX в. появилась информатика – наука, отделившаяся от кибернетики, занимающаяся исследованиями способов получения, хранения, передачи и обработки информации. В промышленно развитых западных обществах информация стала чем-то необходимым, главным и незаменимым компонентом общества. Таким образом, актуальность использования методов передачи и обработки информации (данных) возрастает.
Кодирование – это процесс формирования представления информации, как правило, в удобном для хранения и передачи виде. В связи с развитием информационных технологий кодирование является центральным вопросом при решении самых разных задач, в том числе имеющих отношение к программированию. Преобразование информации в дискретную (набор логических нулей и единиц) или при помощи кодирования может подразумевать:
- Представление данных произвольной структуры (числа, текст, графика) в памяти компьютера;
- Обеспечение помехоустойчивости при передаче данных по каналам связи;
- Шифрование данных;
- Сжатие информации.
Информация, кодирование которой необходимо осуществить, как правило, доступна в виде файлов данных.
Файл данных – это компьютерный файл (именованная область внешней памяти, выделенная для хранения), в котором хранятся данные, используемые компьютерным приложением или системой, включая входные и выходные данные [3.]. Файл данных обычно не содержит инструкций или кода для выполнения (то есть компьютерной программы). Большинство компьютерных программ работают с файлами данных.
Файлы данных могут храниться двумя способами:
- Текстовые файлы;
- Бинарные файлы.
Текстовые файлы (часто называемые ASCII-файлами) хранят информацию в символах кодировки ASCII. Текстовый файл содержит удобочитаемые символы. Пользователь может читать содержимое текстового файла или редактировать его с помощью текстового редактора. В текстовых файлах каждая строка текста заканчивается (разделяется) специальным символов, известным от EOL (от англ. End Of Line – конец строки). Примером текстового файла может служить текстовый документ – файл с расширением .txt.
Бинарные (двоичные) файлы содержат информацию в том же формате, в котором она хранится в памяти, то есть в двоичной форме. В двоичном файле нет разделителей строк и символов перевода. Это позволяет проще и быстрее осуществлять операции чтения и записи, чем при работе с текстовыми файлами [3.]. До тех пор, пока файл не нужно переносить в другую операционную систему либо читать при помощи текстового редактора, двоичные файлы являются лучшим способом хранения информации. Примером бинарного файла может служить изображение в формате JPEG.
Цель данной работы – изучить методы кодирования информации, позволяющие выполнять шифрование и сжатие файлов данных, а также выявление ошибок в файлах.
Для достижения цели в курсовой работе были поставлены следующие задачи:
- изучить методы кодирования, предназначенные для шифрования и дешифрования данных;
- изучить методы кодирования, предназначенные для сжатия файлов данных;
- ознакомиться с теорией циклических избыточных кодов для выявления искажений в сообщениях;
- выбрать язык программирования высокого уровня для программной реализации алгоритмов кодирования с возможностью использования графического пользовательского интерфейса;
- реализовать программы на выбранном языке программирования, а также выполнить тестирование и отладку разработанных программ.
В процессе выполнения работы все поставленные задачи были успешно выполнены.
Методы шифрования данных
Теоретические основы шифрования данных
Актуальность использования криптографических методов обусловлена быстрым развитием сетевых технологий и мощностей вычислительных устройств, а также широким использованием компьютерных сетей, в том числе и глобальной сети Интернет, по которым передаются большие объемы информации государственного, военного, коммерческого и частного характера, не допускающего возможность доступа к ней посторонних лиц. Потребность в криптографии возникла с появлением письменности. Так, например, еще до нашей эры встречались первые криптосистемы – в секретной переписке римского полководца Цезаря был использован шифр подстановки, впоследствии названный его именем. Тем не менее, до появления алгоритма RSA (аббревиатура от фамилий его создателей – Rivest, Shamir и Adleman) все существующие криптосистемы основывались на том факте, что как передающая сообщение сторона, так и принимающая его должны разбираться в принципах работы самого метода шифрования и обладать знанием о единственном ключе для декодирования шифра.
Алгоритм RSA, разработанный в 1977 году Ривестом, Шамиром и Адлеманом, предложил новую модель шифрования – шифрование с открытым ключом. Создатели алгоритма исходили из предпосылки о том, что отправитель сообщения не обязательно должен уметь его расшифровывать. В этой парадигме для шифрования используется так называемый открытый ключ, который может быть опубликован для всех, кто хочет получить доступ к результату шифрования. Для дешифрования используется закрытый ключ, доступный только получателю. Обеспечение конфиденциальности в криптосистеме с открытым ключом состоит в том, что чрезвычайно трудно получить ключ дешифрования из общедоступного ключа шифрования [6.]. Алгоритм работает, используя понятия теории чисел, в том числе теорему Ферма.
Метод Диффи-Хеллмана
Общим слабым местом криптографических систем, существовавших до второй половины XX века, была проблема распределения ключей. Для того, чтобы обмен информацией между двумя сторонами был конфиденциальным, используемый для этого обмена ключ должен быть сгенерирован одной из сторон, а затем безопасно передан другой. Таким образом, даже для передачи самого ключа требовалось использование какой-то криптосистемы. Как передающая сообщение сторона, так и принимающая его должны были разбираться в принципах работы самого метода шифрования и обладать знанием о единственном ключе для декодирования шифра [5.].
Впервые эта проблема была решена Уитфилдом Диффи, работающим в сотрудничестве с Мартином Хеллманом [6.]. Шифр, предложенный Диффи, содержал асимметричный ключ (пару «открытый ключ, закрытый ключ»). В других криптосистемах дешифрование было просто противоположным шифрованию; эти системы использовали симметричный ключ, потому что дешифрование и шифрование симметричны. Несмотря на то, что Диффи разработал общую концепцию асимметричного шифра, у него фактически не было определенной односторонней функции, которая отвечала бы необходимым требованиям. Тем не менее, его статья, опубликованная в 1975 году, вызвала интерес среди других математиков и ученых. Диффи и Хеллман, однако, не смогли продвинуться дальше в разработке нового шифра. Это открытие было сделано группой других исследователей: Ривестом, Шамиром и Адлеманом в 1977-м году [6.].
Пример алгоритма Диффи-Хеллмана.
1 шаг: Алиса и Боб договариваются о значениях для некоторой математической односторонней функции. Значения не являются секретными. Допустим, что эти значения 9 и 14. Функция будет иметь вид 9х (mod 14)
2 шаг: Алиса и Боб выбирают свои случайные числа, которые хранят в секрете. Пусть Алиса выбрала число 5, а Боб – 7. Эти числа обозначаются А и В соответственно.
3 шаг: Алиса и Боб подставляют свои секретные числа в функцию и вычисляют значение. 95 (mod 14) = 59 049 mod 14 = 11. 97 (mod 14) = 4782969 (mod 14) = 9. Эти числа обозначаются С и Е соответственно.
4 шаг: Алиса и Боб обмениваются вычисленными значениями и вычисляют значение функции со своим и полученным числом в качестве аргумента, т.е. Алиса вычисляет ЕА (mod 14), Боб, соответственно, вычисляет СВ (mod 14). 95 (mod 14) = 59 049 mod 14 = 11. 117 (mod 14) = 19487171 mod 14 = 11. Полученное в результате всех операций число 11 будет секретным ключом для шифрования передаваемых данных.
При работе алгоритма Диффи-Хеллмана [5.] каждая сторона:
- Генерирует случайное натуральное число a – закрытый ключ, затем совместно с удалённой стороной устанавливает открытые параметры p и g (обычно значения p и g генерируются на одной стороне и передаются другой), где p является случайным простым числом, g является первообразным корнем по модулю p
- Вычисляет открытый ключ A, используя преобразование над закрытым ключом по формуле (1):
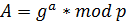
- Обменивается открытыми ключами с удалённой стороной и вычисляет общий секретный ключ K, используя открытый ключ удаленной стороны B и свой закрытый ключ a, формула (2):
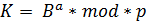
К получается равным с обоих сторон, потому что
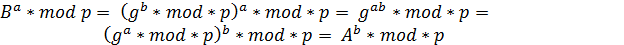
Алгоритм [5.] проиллюстрирован на рисунке 1.
Рисунок 1. Алгоритм Диффи-Хеллмана
Алгоритм RSA
Алгоритм RSA получения открытого и закрытого ключей выглядит следующим образом [5.]:
- Выбрать два простых числа
и
.
- Найти их произведение
, которое называется модулем.
- Найти значение функции Эйлера от числа
:
.
- Выбрать целое число
:
, взаимно простое со значением функции
.
- Найти линейное представление наибольшего общего делителя этих двух чисел:
и вычислить число
(например, при помощи расширенного алгоритма Евклида).
Пара чисел 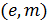
Пара чисел 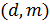
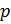
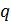
В схеме RSA сообщением являются целые числа, лежащие от 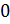
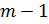
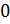
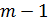
Алгоритм шифрования RSA [3.]:
- Взять открытый ключ
- Взять открытый текст
- Получить криптограмму
:
- Передать шифрованное сообщение
Алгоритм дешифрования [5.]:
- Принять зашифрованное сообщение
.
- Применить закрытый ключ
для расшифровки сообщения
.
Одним из наиболее известных протоколов аутентификации является протокол на основе алгоритма RSA, который состоит из этапов генерации (получения открытого и закрытого ключей) и аутентификации:
До появления Интернета шифрование во многих отношениях считалось проблемой только для государственных учреждений. Алгоритм RSA был введен в то время, когда потенциальная популярность Интернета впервые стала очевидной. С этой популярностью пришел высокий спрос на безопасную и надежную возможность передачи информации. Алгоритм RSA, воспринимаемый как почти неразрушимая криптосистема с открытым ключом, быстро стал ключевым методом выбора для приложений криптографии в Интернете, включая, например, шифрование электронной почты. Сегодня RSA также продолжает использоваться внутри протокола Secure Socket Layer (SSL), используемого в большинстве случаев обмена данными в интернете [1.]. Это позволяет сделать вывод о том, что алгоритм RSA является очень надежной криптосистемой, которая используется в течение последних тридцати лет для обеспечения безопасности в миллионах приложений в Интернете.
Вместе с тем алгоритм был подвергнут ряду криптографических атак, то есть попыток найти и использовать слабые стороны алгоритма. Некоторые из них рассматриваются в следующем разделе. Основа безопасности алгоритма RSA состоит в том, что при заданном 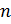
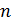
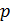
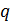
Методы сжатия данных
Основы сжатия данных
Объемы регулярно производимых цифровых данных растут день ото дня. По данным всемирной консалтинговой организации International Data Corporation, общий объем новых данных будет увеличиваться с ежегодным приростом 57%, что опережает ожидаемый рост емкости носителей информации. Поскольку необходимо сохранять большую часть этих данных, всегда существует экономически целесообразная потребность в эффективных цифровых архивах. Наиболее популярные их них используют принцип сжатия данных. Сжатие представляет собой процесс преобразования входного потока данных (исходного потока, или исходных необработанных данных) в другой поток данных (выходной поток, поток битов, или сжатый поток), который имеет меньший размер [14.]. Поток – это файл или буфер в памяти.
Для конечного пользователя потребность сжатия файлов и каталогов на компьютере обусловлена целым рядом причин. Некоторые из них экономят место на диске и используют минимальную пропускную способность для сетевого взаимодействия с передачей файлов. Как правило, архивирование данных означает создание резервной копии и ее сохранение в безопасном месте, которое находится в сжатом формате. Архивный файл состоит из одного или нескольких файлов, включая метаданные в дополнительных полях, таких как имя файла, разрешение и так далее. Архивные файлы обычно используются для объединения нескольких файлов данных в один с целью добиться переносимости и меньшего пространства для хранения [11.].
Предметную область сжатия данных часто называют кодированием для сжатия. Легко представить себе, что входные символы (такие как биты, коды ASCII, байты, аудиосэмплы или значения пикселей) генерируются определенным источником информации и должны быть закодированы перед их отправкой по назначению. Источник может быть без внутренней памяти, но может также иметь память. В первом случае каждый символ не зависит от предшествующих ему, во втором – зависит от некоторых ему предшествующих и, возможно, также от следующих за ним символов, поэтому они взаимосвязаны. Источник данных без памяти также называется «независимым и одинаково распределенным». Сжатие данных достигло своего пика за последние 20 лет. Количество и качество литературы в этой области являются достаточным доказательством.
Существует много известных способов сжатия данных [14.]. Они основаны на разных идеях, подходят для разных типов данных и дают разные результаты, но в основе каждого из них лежит один и тот же принцип – они сжимают данные, удаляя избыточность из исходных данных в исходном файле. Любые неслучайные данные имеют некоторую структуру, и эта структура может быть использована для достижения меньшего представления данных, представления, где структура не различима. Термины «избыточность» и «структура» используются в профессиональной литературе, равно как и «гладкость», «согласованность» и «корреляция»; все они относятся к одному и тому же понятию. Таким образом, избыточность является ключевым понятием в любой дискуссии о сжатии данных.
Идея сжатия путем уменьшения избыточности формулирует общий закон сжатия данных, который заключается в том, чтобы «присваивать короткие коды общим событиям (символы или фразы) и длинные коды редким событиям». Существует много способов реализации этого закона, и анализ любого метода сжатия демонстрирует, что в своей фундаментальной реализации он работает, подчиняясь общему закону.
Сжатие данных осуществляется путем изменения их представления с неэффективного (то есть длинного) на эффективное (короткое). Следовательно, сжатие возможно только потому, что данные обычно представлены на компьютере в формате, который длиннее, чем это в целом требуется. Причина того, что неэффективные (длинные) представления данных используются постоянно, состоит в том, что эти представления облегчают их обработку, а обработка данных является более распространенной практикой и более важной, чем сжатие. Кодировка ASCII для символов является хорошим примером представления данных, которое длиннее, чем это необходимо. Она использует 7-битные коды, потому что с кодами фиксированного размера легко работать. Однако коды переменного размера были бы более эффективными, поскольку некоторые символы используются чаще других, и поэтому им могут быть назначены более короткие коды. В мире, где информация всегда представлена в кратчайшем формате, невозможно будет сжимать данные.
Принцип сжатия путем удаления избыточности [15.] также отвечает на следующий вопрос: «Почему уже сжатый файл не может быть сжат в дальнейшем?» Ответ, конечно же, заключается в том, что такой файл имеет небольшую избыточность или не имеет ее вообще, поэтому из него уже ничего нельзя удалить. Примером такого файла является случайный текст. В случайном тексте каждая буква встречается с равной вероятностью, поэтому присвоение символам кодов фиксированного размера не добавляет избыточности. Когда такой файл сжимается, избыточность для удаления отсутствует. Другой ответ на вопрос заключается в том, что если бы можно было сжимать уже сжатый файл, то последовательные сжатия уменьшали бы размер файла до тех пор, пока он не станет занимать всего лишь один байт или даже один бит в памяти компьютера. Это, конечно, невозможно, поскольку один байт не может содержать информацию, представленную в сколь угодно большом файле.
Как правило, файлы со случайными данными встречаются редко, но есть еще один хороший пример с ранее сжатым файлом. Владелец сжатого файла, как правило, знает, что он уже сжат, и не будет пытаться сжимать его дальше, но существует одно исключение при передаче данных модемами. Современные модемы содержат оборудование для автоматического сжатия отправляемых данных, и, если эти данные уже сжаты, дальнейшего сжатия не будет. Возможно даже расширение данных. Вот почему модем обязан отслеживать степень сжатия «на лету», а если она низкая, он должен прекратить сжатие и передавать оставшиеся данные без него.
Методы сжатия без потерь создают файл меньшего размера, чем исходный, который можно использовать для восстановления исходного файла. Эти методы используют некоторые алгоритмы для определения повторяющихся частей внутри файла, где всегда создается список переменных, которые определяют блоки данных. Фактически все методы сжатия без потерь используют двухэтапный процесс: сначала сопоставляют сильно повторяющиеся значения с чем-то менее повторяющимся, на что можно легко ссылаться, а затем изменяют вхождения всех этих значений с помощью ссылок.
Кроме того, современные методы сжатия без потерь [11.] являются адаптивными, поскольку они не просматривают весь входной файл и не создают словарь ссылок, который должен быть заменен. Вместо этого они анализируют файл, когда начинают его читать, и воссоздают словарь, основываясь на том, какие данные в действительности повторяются. Словарь становится более информативным и объемным по мере продолжения процесса.
Архивы и форматы архивных файлов
Архивный файл (архив) – это файл, который состоит из одного или нескольких компьютерных файлов вместе с метаданными (метаинформацией). Архивные файлы используются для объединения нескольких файлов данных в один с целью облегчить переносимость и хранение этих файлов, или просто для сжатия файлов с целью уменьшения места для их хранения. Архивы часто хранят структуры каталогов, информацию об обнаружении и исправлении ошибок (как правило, контрольные суммы), произвольные комментарии, а иногда используют встроенное шифрование (шифруя данные при помощи пароля).
Некоторые архивы могут быть оформлены в виде программ [17.]. Они являются самораспаковывающимися – для распаковки содержимого такого архива не требуется иметь совместимую с ним программу-архиватор.
Использование архивов имеет ряд преимуществ:
- удобство ориентации в файловом пространстве;
- экономия места;
- надежность хранения информации.
При создании многофайлового архива можно добавить специальную информацию для восстановления данных и указать пароль для ограничения доступа. Если произойдет повреждение какого-либо файла (из-за технических проблем устройства или по другим причинам), то открыть его будет почти невозможно. Добавив в архив информацию для восстановления, с большой вероятностью можно восстановить данные в архиве. Наличие пароля также обеспечивает приватность хранимой информации.
Кроме того, многие интернет-сервисы ограничивают разрешенные для загрузки типы файлов. Оптимальным решением в данных случаях будет архив информации. В нем может храниться как один файл, так и папка с множеством подкаталогов и файлов. Использование архивов для обмена информацией в интернете является стандартом де-факто.
Формат архива – это файловый формат архивного файла. Существует множество форматов для различных архивных файлов, но лишь некоторые из них получили широкое признание и поддержку со стороны поставщиков программного обеспечения и пользовательских сообществ.
Программистам UNIX-подобных систем хорошо известна стандартная утилита ar, так как она широко используется даже сегодня для создания статических библиотек, которые являются не чем иным, как архивами скомпилированных файлов. Утилита ar может использоваться для создания архивов всех видов. Как правило, файлы пакетов .deb в системах Debian – это не что иное, как ar-архивы. А пакеты mpkg в MacOS X – это сжатые gzip-архивы cpio. Формат tar более популярен среди пользователей, чем thanar и cpio, поскольку команда tar была действительно хорошей и простой в использовании [11.].
RAR – это хорошо известный формат архивных файлов, который используется для сжатия данных, восстановления после ошибок и охвата файлов [11.]. Структурно файл RAR состоит из блоков переменной длины обязательных и необязательных данных. Точность создания блоков со временем развивалась от версии к версии. Первоначально файл RAR состоял из маркера или вводного блока, архивного блока, который состоял из заголовка архива и заголовка файла, и закрывающего блока, который состоял из дополнительных комментариев или другой информации, необходимой для правильной обработки файла. Порядок этих блоков мог варьироваться, но первый блок должен быть вводным блоком, за которым следует блок заголовка архива. Блок архива очень сложен, потому что он содержит заголовки своих архивов, а также заголовки файлов [18.].
Формат файла ZIP был введен в конце 1980-х годов для утилиты PKZIP. Он обновлялся из года в год, и теперь включает в себя различные алгоритмы сжатия. Не всегда случается так, что ZIP-алгоритмы являются наиболее эффективными или действенными – у них есть много других конкурентов, которые могут работать лучше во многих ситуациях, но общая производительность этих алгоритмов хорошая. Формат файла ZIP используется во многих продуктах, таких как файлы JAR Java, файлы проекта SAS Enterprise Guide и т.д. Формат ZIP поддерживается Windows, поэтому он специально используется в кроссплатформенных средах [14.].
После десятилетия внедрения tar формат ZIP также появился в мире MS-DOS в качестве формата архива, поддерживающего сжатие. Самым распространенным методом сжатия, используемым в ZIP, является deflate, который представляет собой не что иное, как реализацию алгоритма LZ77. Но формат ZIP-файла, разработанный PKWARE для коммерческих целей, годами сталкивался с препятствиями для патентов. Формат gzip был создан для реализации алгоритма LZ77 в свободном программном обеспечении без нарушения каких-либо патентов PKWARE, который использовался только для сжатия файлов. Таким образом, чтобы создать сжатый архивный файл, сначала необходимо создать архивный файл, используя, например, утилиту tar, затем сжать этот архивный файл и получить файл tar.gz (иногда сокращенно .tgz).
tar-файл – это обычный архивный файл, в котором данные находятся не в сжатом виде. Другими словами, при создании tar из 100 файлов размером 50 КБ можно получить архив, размер которого составит около 5000 КБ. Единственный выигрыш, который можно ожидать при использовании только формата tar, – это предотвращение потери используемой памяти файловой системой, поскольку большинство из них выделяют пространство с определенной степенью детализации (например, в некоторых системах однобайтовый файл использует 4 КБ дискового пространства, 1000 из них потребуют 4 МБ, но соответствующий архив tar просто требует 1 МБ) [17.].
По мере развития компьютерных наук было разработано еще несколько алгоритмов для достижения более высокой степени сжатия. Например, алгоритм Барроуза-Уилера, используемый в bzip2 (сокращение с tar.bz2 архива), или популярный в последнее время Timesxz, который реализует алгоритм LZMA, используемый в утилите 7zip.
Tar поддерживает множество программ сжатия, таких как gzip, bzip2, lzip, lzma, lzop, xz. Из них gzip, вероятно, наиболее широко используемый инструмент хранения, используемый в системах Unix и Linux. Для сжатия данных используется алгоритм Лемпеля-Зива (LZ77).
Формат gzip использует технику сжатия, известную как Deflate. Этот алгоритм также используется в некоторых других популярных технологиях, таких как формат файла изображения PNG, веб-протокол HTTP и протокол защищенной оболочки SSH. Одним из главных его преимуществ является скорость. Он может сжимать, а также распаковывать данные с гораздо большей скоростью, чем другие конкурирующие технологии, особенно при сравнении самых компактных форматов сжатия этих утилит. Он также очень эффективен с точки зрения использования памяти во время сжатия и распаковки, и не требует памяти при оптимизации для наилучшего сжатия. В то время как gzip использует алгоритм Deflate, bzip2 является реализацией алгоритма Берроуза-Уилера.
Важный момент для пользователей – большее сжатие за счет более длительного времени сжатия. bzip2 может создавать более компактные файлы, чем gzip, но для достижения результатов требуется много времени из-за более сложного алгоритма. Требуемое время распаковки меньше по сравнению со временем сжатия, поэтому может быть преимуществом использование формата файла bzip2, так как в этом случае нужно только понести временные потери во время сжатия и иметь возможность использовать сжатые файлы меньшего размера, которые можно распаковать в сравнительно короткие сроки. Время, необходимое для распаковки, все еще намного больше, чем gzip, но не оказывает такого большого влияния, как операция сжатия. Также следует отметить, что требования к памяти у bzip2 больше, чем у gzip.
Утилиты сжатия xz влияют на алгоритм сжатия [11.], известный как LZMA2. Этот алгоритм имеет большую степень сжатия по сравнению с двумя приведенными выше примерами, и это предпочтительный формат, когда требуется хранить данные на ограниченном дисковом пространстве. Он дает сравнительно меньшие файлы, что снова приводит к тем же нюансам, которые есть у bzip2. В то время как сжатые файлы, которые создает xz, меньше, чем у других инструментов, для сжатия требуется значительно больше времени. У утилиты сжатия xz также больше требований к памяти, иногда она на порядок выше, чем у других утилит. При работе в системе с достаточным объемом памяти, это может не быть значительной проблемой, но стоит подумать над этим нюансом.
Основное отличие между этими форматами состоит в том, что bzip2 использует алгоритм сжатия текста с сортировкой блоков алгоритмом Берроуза-Уилера в сочетании с кодированием Хаффмана вместо алгоритма LZ77, который используется в gzip. Техника сжатия bzip2 дает более эффективное сжатие, чем gzip, однако метод сжатия bzip2 обычно является более сложным и занимает больше времени (т.е. использует больше циклов ЦП), чем сжатие gzip [17.].
Формат RAR использует необязательное шифрование AES, которое является типом блочного шифра и задействует алгоритм, который шифрует данные в каждом блоке. Существуют различные типы стандартов AES и реализаций, используемых RAR, которые меняются в зависимости от версии. RAR5 (текущая версия) использует AES-256, а не AES-128, используемый в RAR4 [18.]. Формат RAR стал более популярным с годами по сравнению с конкурирующими форматами архивов, такими как 7Z, zip и т. д., поскольку он имеет более высокую скорость сжатия данных, чем ZIP, и использует метод сжатия без потерь [19.].
Что касается .jpg, .mp3, .mp4 и подобных им форматов, то практически общеизвестно, что это сжатые файлы данных. Менее известным является тот факт, что все они используют деструктивное сжатие. Это означает, что невозможно воспроизвести точно такое же изображение после технологии сжатия JPEG. Из-за этого обстоятельства сжатие изображений JPEG или файлов MP3 / MP4 не принесет значительных результатов.
На сегодняшний день есть возможность свободно использовать любой формат файла архива как в Linux, так и в Windows. Но формат файла zip имеет встроенную поддержку в Windows, и это особенно используется в кроссплатформенных средах. Также можно обнаружить формат файла zip в разных местах. Например, он также использовался Sun для JAR-архивов при распространении скомпилированных программ Java или для файлов Open Document (.odf, .odp и т.д.), используемых LibreOffice и некоторыми другими офисными пакетами. Все эти форматы файлов являются ничем иным, как zip-архивами.
Все еще в пользу формата архива tar говорит тот факт, что формат файла zip в полной мере не поддерживает все метаданные файловой системы Unix. По некоторым причинам следует иметь в виду, что формат файла ZIP определяет только ограниченный набор обязательных атрибутов файла: имя файла, дата изменения, разрешения [19.]. Помимо этих основных атрибутов, архиватор может хранить некоторые дополнительные метаданные в дополнительных полях заголовка ZIP-файла, но эти дополнительные поля зависят от реализации, и даже у эффективных архиваторов нет гарантий хранения или извлечения одного и того же набора метаданных.
Алгоритмы сжатия данных
Алгоритм RLE (Run Length Encoding). Основная идея алгоритма RLE состоит в выявления повторяющихся последовательностей данных и замены их более простой структурой, в которой указывается код данных и коэффициент повторения. Несмотря на то, что кодер RLE, как правило, дает очень незначительное сжатие, он может работать очень быстро. А скорость работы декодера RLE вообще близка к скорости простого копирования блока информации. К положительным сторонам алгоритма, можно отнести то, что он не требует дополнительной памяти при работе, и быстро выполняется. Алгоритм применяется в форматах РСХ, TIFF, ВМР. Интересная особенность группового кодирования в PCX заключается в том, что степень архивации для некоторых изображений может быть существенно повышена всего лишь за счет изменения порядка цветов в палитре изображения.
Алгоритмы группы KWE (KeyWord Encoding). В основу алгоритма сжатия по ключевым словам положен принцип кодирования лексических единиц группами байт фиксированной длины. Примером лексической единицы может быть обычное слово. На практике на роль лексических единиц выбираются повторяющиеся последовательности символов, которые кодируются цепочкой символов (кодом) меньшей длины. Результат кодирования помещается в таблице, образовывая так называемый словарь. Алгоритмы сжатия этой группы наиболее эффективны для текстовых данных больших объемов и малоэффективны для файлов небольших размеров (за счет необходимости сохранение словаря).
Алгоритм Хаффмана. В основе алгоритма Хаффмана лежит идея кодирования битовыми группами. Сначала проводится частотный анализ входной последовательности данных, то есть устанавливается частота вхождения каждого символа, встречающегося в ней. После этого, символы сортируются по уменьшению частоты вхождения.
Основная идея состоит в следующем: чем чаще встречается символ, тем меньшим количеством бит он кодируется. Результат кодирования заносится в словарь, необходимый для декодирования.
Сравнение алгоритмов приведено в таблице ниже.
Сравнение алгоритмов сжатия данных
|
Название |
Выходная структура |
Сфера применения |
Явные плюсы |
Явные минусы |
|
RLE |
Список |
Графические данные |
1. Не требует дополнительной памяти при работе 2. Эффективность не зависит от объема 3. Высокая скорость работы |
1.Ограниченный круг применения. 2. Низкая степень сжатия |
Сравнение алгоритмов сжатия данных (продолжение таблицы)
|
Название |
Выходная структура |
Сфера применения |
Явные плюсы |
Явные минусы |
|
KWE |
Таблица словаря |
Текстовые данные |
2. Хорошая скорость работы. |
1.Ограниченный круг применения 2.Малоэффективны при работе с маленькими объемами данных |
|
Алгоритм Хаффмана |
Дерево кодировки |
Любые данные |
1.Универсальность 2. Не увеличивает объем при неудаче (не считая таблицы) |
1. Эффективен для большого объема данных. 2. Двухэтапная обработка |
Теория циклических избыточных кодов
Основные положения
Теория циклических избыточных кодов, несмотря на свое давнее появление (конец 60-х годов XX столетия) по-прежнему остается актуальной. Циклические избыточные коды широко использовались на протяжении десятилетий в компьютерной индустрии для того, чтобы можно было гарантировать правильную запись блоков на дисках и магнитных лентах. Они также широко используются для кодирования и декодирования пакетных ошибок канала связи, где временный сбой может вызвать сразу несколько смежных ошибок данных. Кроме того, циклические избыточные коды принимают участие в механизме встроенного самотестирования (англ. built-in self-testing – BIST) и для тестирования ПЗУ памяти.
Циклический избыточный код (англ. Cyclic Redundancy Check, CRC) – это код проверки ошибок, который широко используется в системах передачи данных и других системах последовательной передачи. CRC представляет собой алгоритм нахождения контрольной суммы, проверяющий целостность данных. Он основан на полиномиальных манипуляциях с использованием модульной арифметики. Некоторыми из распространенных стандартов проверки циклическим избыточным кодом являются CRC-8, CRC-12, CRC-16, CRC-32 и CRC-CCIT.
Методы обнаружения ошибок предназначены для выявления искажений в сообщениях при их передаче по зашумленным каналам. Для этого передающее устройство вычисляет некоторое число, называемое контрольной суммой и являющееся функцией сообщения, и добавляет его к этому сообщению. Приемное устройство, используя тот же самый алгоритм, рассчитывает контрольную сумму принятого сообщения и сравнивает ее с переданным значением [15.].
Под контрольной суммой CRC (Cyclic Redundancy Check) понимается некоторое значение, рассчитанное по набору данных путем применения математических алгоритмов, обеспечивающих устойчивость к хэш-коллизиям [7.]. Под хэш-коллизией понимается равенство контрольных сумм для различных входных данных. Контрольные суммы широко применяются для осуществления контроля правильности хранимой и передаваемой информации.
Логической предпосылкой использования контрольной суммы этого типа явилось то, что размер контрольной суммы значительно меньше формата преобразуемых чисел/сообщений, следовательно, вероятность искажения контрольной суммы (при передаче информации по какому-либо каналу или при ее хранении на носителе) значительно ниже вероятности искажения массива информации.
Циклические избыточные коды (CRC) являются подклассом блочных кодов и применяются в протоколах HDLC, Token Ring, Token Bus, в семействах протоколов Ethernet и других протоколах канального уровня. Популярность CRC-кодов обусловлена тем, что процедуры кодирования и декодирования достаточно просты и не требуют больших вычислительных ресурсов.
В сетевых системах значительная роль уровня канала передачи данных заключается в преобразовании потенциально ненадежного физического канала между двумя компьютерами в максимально надежный канал. Это достигается путем включения избыточной информации в каждый передаваемый фрейм данных. В зависимости от характера канала и данных, можно включить достаточно избыточности, чтобы можно было обнаружить ошибки и затем организовать повторную передачу поврежденных кадров. Проверка при помощи CRC является широко используемой схемой обнаружения ошибок на основе битов четности в приложениях последовательной передачи данных. Этот код основан на полиномиальной арифметике. Биты данных, которые должны быть переданы, являются коэффициентами полинома. В качестве примера, битовый поток 1101011011 имеет 10 битов, представляющих полином десятой степени:
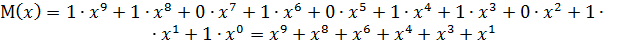
Для того, чтобы вычислить CRC сообщения, выбирается другой многочлен, называемый порождающим полиномом G(x). G(x) должен иметь степень больше нуля и меньше, чем у многочлена M(x). Другое требование для G(x) – это ненулевой коэффициент члена x0. Это приводит к нескольким возможным вариантам полинома-генератора и, следовательно, к необходимости стандартизации. CRC-16 является одним из таких стандартов, который использует генерирующий полином:
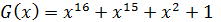
CRC-16 обнаруживает все единичные и двойные ошибки, все ошибки с нечетным числом битов, все пакетные ошибки длиной 16 или менее и большинство ошибок для более длинных пакетов.
CRC-32 использует другой генераторный полином:
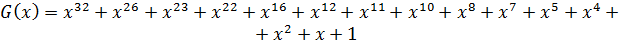
В общем случае n-битный CRC вычисляется путем представления потока данных в виде полинома M(x), умножения M(x) на xn (где n – степень полинома G(x)) и деления результата на порождающий полином G(x). Полученный остаток добавляется к многочлену M(x) и передается по каналу. Полный переданный полином затем делится на этот же порождающий полином на стороне получателя. Если результат этого деления не имеет остатка, это означает, что нет ошибок передачи. Математически это можно представить так:
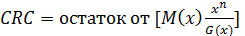
Выбор порождающего полинома является одной из важнейших задач построения CRC-кодов. Как правило, этот выбор обусловлен рекомендациями и стандартами реально существующих организаций, которые используют те или иные спецификации алгоритмов CRC.
Самый популярный и рекомендуемый IEEE полином для CRC-32 используется в Ethernet, FDDI; также этот многочлен является генератором кода Хемминга [8.]. Использование другого полинома – CRC-32C – позволяет достичь такой же производительности при длине исходного сообщения от 58 бит до 131 кбит, а в некоторых диапазонах длины входного сообщения может быть даже выше – поэтому в наши дни он тоже пользуется популярностью [13.]. К примеру, стандарт ITU-T G.hn использует CRC-32C с целью обнаружения ошибок в полезной нагрузке.
Полином (3) в шестнадцатеричном виде выглядит как 0x04C11DB7 – этот многочлен является рекомендованным для стандарта IEEE 802 с подгруппой 802.3. Эта подгруппа является основой семейства технологий пакетной передачи данных Ethernet. IEEE 802.3 определяет многочлен M(x) как адрес назначения, адрес источника, длину / тип и данные фрейма с добавлением первых 32-битных данных. Остаток от вычисления CRC выше дополняется, и в результате получается 32-битный CRC IEEE 802.3, называемый полем Frame Check Sequence (FCS). FCS добавляется в конец кадра Ethernet и передается первым битом высшего порядка (x31, x30, …, x1, x0).
Одним из основных условий для выбора многочлена является то, что коэффициенты в старшем и младшем битах равны единице. Математическая модель нахождения контрольной суммы может быть записана следующим образом:
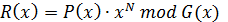
где
R(x) – полином, представляющий значение CRC;
P(x) – полином, коэффициенты которого представляют входные данные;
G(x) – порождающий полином;
N – степень порождающего полинома (1 ≤ N ≤ 256).
Алгоритмы вычисления циклических избыточных кодов
Прямой алгоритм вычисления CRC определяет контрольную CRC побитно [9.], его можно описать следующим образом в соответствии с (5):
1) дополнить исходное сообщение нулями для выравнивания (количество нулей обусловливается степенью порождающего полинома). P(x)´ = P(x)000…N;
2) выполнять операцию сдвига влево последовательности бит сообщения P(x)´ до тех пор, пока бит в ячейке не станет равным единице или количество бит станет меньше, чем в делителе;
3) если старший бит станет равным единице, то произвести операцию XOR между сообщением и порождающим полиномом и повторить шаг 2;
4) конечный остаток от последовательности P(x)´ является CRC-остатком.
В приведенном описании G(x) – полином, N – степень полинома, P(x) – исходное сообщение, а P(x)´ – дополненное исходное сообщение.
Необходимость выполнения множества итераций при генерации контрольной суммы CRC приводит к значительным временным затратам.
Табличный алгоритм вычисления CRC используется для ускорения расчета контрольной суммы CRC [10.].
Ускорение осуществляется за счет замены восьми операций сдвига одной операцией поиска по таблице, которая содержит 256 значений. Поэтому при расчете контрольной суммы CRC выполняется цикл по 256 значениям.
Предпосылкой появления таблицы явилось то, что при выполнении операции XOR содержимого с постоянной величиной при различных ее сдвигах всегда будет существовать некоторое значение, которое при применении операции XOR с исходным содержимым даст тот же самый результат [2.]. Следовательно, можно составить таблицу таких величин, где индексом является исходное содержимое [15.].
Алгоритм составления таблицы:
1) вычислить значение в таблице для каждого байта от 0x00 до 0xff:
а) выполнять 8 раз операцию «сдвиг вправо», причем, если младший бит равен 1, то выполняется операция XOR с полиномом G;
б) все что осталось от двух байт, становится значением в таблице.
Алгоритм вычисления контрольной суммы CRC по таблице:
1) просматривается каждый байт сообщения P(x):
а) над младшим байтом текущего значения CRC и текущим байтом сообщения проводится операция XOR – это индекс в таблице;
б) старший байт текущего значения CRC сдвигается вправо на 8 и становится младшим, затем объединяется по XOR со значением таблицы – это будет новое значение CRC;
2) в результате получено значение CRC.
Практическая реализация алгоритмов
Выбор языка и среды разработки
Данный раздел посвящен разработке простых прикладных программ с графическим интерфейсом пользователя. Учитывая цели данной курсовой работы, в качестве языка программирования был выбран язык высокого уровня C# версии 7.0 как один из наиболее популярных среди современных языков программирования, предназначенных для обучения. В качестве среды разработки выбрана Visual Studio 2019 Community. Выбор среды разработки для реализации программного приложения был мотивирован тем, что выбираемая среда должна быть простой в использовании, чтобы позволить сосредоточиться на изучении концепций программирования, а также многофункциональной для того, чтобы научиться создавать простые программы для решения прикладных задач [16.].
В качестве проектируемых приложений рассматриваются две программы с графическим пользовательским интерфейсом. Первая из рассматриваемых программ позволяет вычислять контрольные суммы файлов, выбранных пользователем, при помощи алгоритма CRC-32, вторая – выполнять шифрование и дешифрование текста, заданного пользователем, при помощи алгоритма RSA. Для реализации был выбран интерфейс программирования приложений Windows.Forms, являющийся частью Microsoft .NET Framework. С помощью Windows.Forms можно создавать приложения с полнофункциональным графическим интерфейсом, в то же время простые в использовании и обновлении [4.]. Выбранный язык программирования вместе со средой разработки позволяет полностью реализовать программу, отвечающую всем предъявленным ей требованиям [12.].
Разработка программного кода для алгоритма CRC-32
При разработке приложения учитывалась специфика алгоритма; его основные принципы легли в основу поставленной задачи. Пользователь имеет возможность выбрать входной файл (один или несколько) для того, чтобы получить результат вычисления его контрольной суммы. Файл передается на вход программе в виде байтового потока.
Вычисление контрольной суммы производится в соответствии с алгоритмами, рассмотренными в подразделе 3.2. В листинге 1 приведен фрагмент программы, выполняющий построение таблицы, в листинге 2 – фрагмент программы, выполняющий вычисление CRC в соответствии с построенной таблицей.
Листинг 1. Исходный код для реализации алгоритма построения таблицы CRC-32
for (int i = 0; i< 256; i++)
{
Crc32 = (uint) i;
for (int j = 8; j > 0; j—)
if ((Crc32 & 1) == 1)
Crc32 = (Crc32 >> 1) ^ POLYNOMIAL;
else
Crc32 >>= 1;
table_CRC32[i] = Crc32;
}
Листинг 2. Исходный код для реализации вычисления контрольной суммы в соответствии с таблицей CRC-32
int count = stream.Read(buffer, 0, buffer_size);
while (count > 0)
{
for (int i = 0; i < count; i++)
result = ((result) >> 8) ^ table_CRC32[(buffer[i]) ^ ((result) & 0x000000FF)];
count = stream.Read(buffer, 0, buffer_size);
}
Полный исходный код программы приведен в приложении 1.
Тестовый пример, приведенный в данном подразделе, можно рассматривать как руководство пользователя. Для запуска программы достаточно запустить файл CRC32List.exe. Программа корректно работает в MS Windows 7/8/10. Установка не требуется.
Пример работы программы после запуска и перетаскивания файлов в область экрана (в список на форме приложения) приведен на рисунке 2. Для проверки были взяты файлы текущего проекта программы.
На рисунке 3 приведен результат вычисления контрольных сумм при помощи программы WinRAR (проект приложения был архивирован в формате .zip). Как следует из рисунка 3, контрольные суммы всех файлов одинаковы. Таким образом, программа работает корректно.
Рисунок 2 – Результат работы программы
Рисунок 3 – Результат вычисления контрольных сумм при помощи программы WinRAR
Разработка программного кода для алгоритма RSA
При разработке приложения учитывалась специфика алгоритма; его основные принципы легли в основу поставленной задачи. Пользователь имеет возможность дешифровать введенный текст, используя закрытый ключ 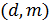
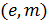
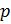
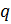
При вводе чисел 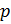
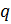
Листинг 3. Исходный код функции Миллера-Рабина
public static bool MillerRabin(int n, int k)
{
for (int i = 0; i < k; i++) // цикл по количеству раундов
{
// проверка элементарных случаев:
if (n % 2 == 0)
return false;
if (n == 2)
return true;
if (n <= 1)
return false;
// представление n — 1 как 2 ^ s * m
int s = 0;
int m = n — 1;
while (m % 2 == 0)
{
s++;
m = m / 2;
}
// выбор случ. целого числа a в отрезке [2, n − 2]
Random r = new Random();
int a = r.Next(n — 1) + 1;
// поиск mod = a ^ m % n
int temp = m;
long mod = 1;
for (int j = 0; j < temp; j++)
mod = (mod * a) % n;
// вычислить в цикле mod как mod ^ 2 % n
while (temp != n — 1 && mod != 1 && mod != n — 1)
{
mod = (mod * mod) % n;
temp *= 2;
}
// если mod = 1, то составное
// если mod != n — 1, то составное
if (mod != n — 1 && temp % 2 == 0)
return false;
}
return true; // вернуть «вероятно простое»
}
В основной программе для реализации шифрования и дешифрования используется две основных функции – getEncryptedText и getDecryptedText соответственно. Каждая из них является методом класса RSA, в котором реализована основная логика приложения. В зависимости от способа задания значений 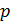
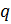
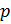
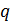
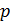
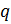
Листинг 4. Исходный код методов шифрования и дешифрования
private string encrypt(int symbol, BigInteger keyE, BigInteger keyN)
{
return BigInteger.ModPow(symbol, keyE, keyN).ToString();
}
private int decrypt(int symbol, BigInteger keyD, BigInteger keyN)
{
return (int)(BigInteger.ModPow(symbol, keyD, keyN));
}
private string textEncrypt(string text, BigInteger e, BigInteger n)
{
string eText = «»;
foreach (var symbol in text)
eText += encrypt(symbol, e, n) + this.blockSep;
return eText;
}
private string textDecrypt(string text, BigInteger d, BigInteger n)
{
string[] arr = text.Split(this.blockSep);
string dText = «»;
foreach (var symbol in arr)
if (symbol != string.Empty)
dText += Convert.ToChar(decrypt(int.Parse(symbol), d, n));
return dText;
}
Для работы с длинными числами здесь используется тип данных BigInteger. Этот целочисленный тип данных отображается на тип System.Numerics.BigInteger библиотеки Microsoft .NET Framework, позволяющий записывать и обрабатывать целые числа практически неограниченной длины. Для данных типа BigInteger реализованы арифметические операции сложения, вычитания, умножения и деления. Операция деления, в отличие от других целочисленных типов данных, возвращает не вещественное значение, а результат целочисленного деления, имеющий тип BigInteger. Метод класса BigInteger.ModPow(p, q, k) возвращает остаток от целочисленного деления на k значения p в степени q.
Функция generatePQ генерирует значения 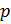
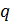
Простые числа выбираются из диапазона (10000, 20000) – генерируется пара чисел, каждое из которых проверяется на простоту при помощи алгоритма Миллера-Рабина с 10 раундами до тех пор, пока оба выбранных числа не окажутся простыми. Исходный код функции представлен в листинге 5.
Листинг 5. Исходный код функции генерации p и q
private void getPrimeNum(Random rnd, out int n1, out int n2)
{
int firstNumber;
int secondNumber;
do
{
firstNumber = rnd.Next(10000, 20000);
secondNumber = rnd.Next(10000, 20000);
}
while (!Utilities.MillerRabin(firstNumber, 10) || !Utilities.MillerRabin(secondNumber, 10));
n1 = firstNumber;
n2 = secondNumber;
}
Набор методов для алгоритма RSA получения открытого и закрытого ключей, описанного в разделе 1, приводится в листинге 6. Функция NOD вычисляет НОД (Наибольший Общий Делитель) для проверки взаимной простоты в методе нахождения числа e. Вызов методов осуществляется внутри функции generatePQ, которая инициализирует поля класса RSA значениями для открытого и закрытого ключей.
Листинг 6. Набор методов для получения открытого и закрытого ключей в соответствии с алгоритмом RSA
// 2. найти модуль
private BigInteger getN(int p, int q)
{
return p * q;
}
// 3. найти значение функции Эйлера fi
private BigInteger getFi(int p, int q)
{
return (p — 1) * (q — 1);
}
// 4. выбрать число е, взаимное простое с fi
private BigInteger getPrime(Random rnd, BigInteger fi)
{
BigInteger e = rnd.Next(1, Math.Abs((int)fi));
do
{
if (NOD(e, fi) == 1)
break;
else e++;
} while (true);
if (e >= fi)
{
e—;
do
{
if (NOD(e, fi) == 1)
break;
else e—;
} while (true);
}
return e;
}
// 5. найти d при помощи расширенного алгоритма Евклида
private BigInteger getD(BigInteger e, BigInteger fi)
{
BigInteger i = fi, v = 0, d = 1;
while (e > 0)
{
BigInteger t = i / e, x = e;
e = i % x;
i = x;
x = d;
d = v — t * x;
v = x;
}
v %= fi;
if (v < 0)
v = (v + fi) % fi;
return v;
}
Полный исходный код программы приведен в приложении 1.
Тестовый пример, приведенный в данном подразделе, можно рассматривать как руководство пользователя. Для запуска программы достаточно запустить файл RSAForm.exe. Программа корректно работает в MS Windows 7/8/10. Установка не требуется.
Пример шифрования при помощи ввода текста в верхнее текстовое и нажатия кнопки «Зашифровать» приведен на рисунке 4.
Рисунок 4 – Шифрование текста с генерацией p и q
При выборе ручного ввода значений 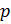
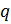
Рисунок 5 – Сообщение об ошибке при попытке ручного ввода чисел
Функции приложения могут быть проверены без ввода секретного ключа. Для этого необходимо, не меняя результат шифрования текста в нижнем текстовом поле, нажать кнопку «Расшифровать» в левой верхней части окна (рисунок 6). Результат представлен на рисунке 7.
Рисунок 6 – Выбор дешифрования только что зашифрованного текста
Рисунок 7 – Результат дешифрования только что зашифрованного текста
На рисунке 8 приведен результат шифрования при помощи значений p и q, заданных вручную.
Рисунок 8 – Шифрование текста при помощи заданных вручную значений p и q
Для дешифрования этого текста необходимо использовать закрытый ключ. Результат такого дешифрования приведен на рисунке 9.
Рисунок 9 – Результат дешифрования при помощи закрытого ключа
ЗАКЛЮЧЕНИЕ
В работе были изучены методы кодирования данных, среди которых подробно рассмотрены сжатие данных и шифрование информации. Получено представление о теории циклических избыточных кодов.
Сжатие и архивация данных являются удобными способами использовать связанные между собой файлы вместе, позволяя при этом значительно сэкономить занимаемое пространство. Однако при работе с различными форматами архивов важно осознавать недостатки производительности и проблемы совместимости, которые могут встречаться в каждом из этих решений. Насколько большое внимание конечные пользователи должны уделять этим деталям, полностью зависит от устройств, на которых они работают.
Сжатие файлов экономит место для хранения и ускоряет передачу данных, но оно также может занять много времени. Сжатие данных требует значительных ресурсов процессора, а сжатие набора данных в несколько терабайт может потребовать огромных вычислительных мощностей.
В ходе выполнения работой было выполнено ознакомление с понятием шифрования с открытым ключом и подробно рассмотрены алгоритмы RSA и Диффи-Хеллмана. Также было выполнено ознакомление с ключевыми понятиями теории циклических избыточных кодов, подробно рассмотрен алгоритм CRC, сформулированы алгоритмы построения таблицы и вычисления контрольной суммы по этому алгоритму. Также было выполнено обоснование выбора языка программирования и среды разработки, итогом которого стала реализация алгоритмов RSA и CRC на языке высокого уровня C# в виде оконных приложений Windows.Forms в среде Visual Studio 2019.
Разработанные программы имеют понятный графический интерфейс, выводят все необходимые пояснения и подсказки, являются законченными и удобными для использования. Таким образом, цели и задачи курсовой работы выполнены в полном объеме.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
- Аршинов М. Н. Коды и математика / М.: Наука, 1983. – 257 с.
- Буркатовская Ю. Б. Быстродействующие алгоритмы деления полиномов в арифметике по модулю два / Ю. Б. Буркатовская, А. Н. Мальчуков, А. Н. Осокин // Изв. Томск. политехн. ун-та. – 2006. – № 1 (309). – с. 19–24.
- Демидович, Е.М. Основы алгоритмизации и программирования. Учебное пособие / Е. М. Демидович. — 2-е изд., испр. и доп. — СПб. : БХВ — Петербург, 2008. — 440 с.
- Документация по семейству продуктов Visual Studio [Электронный ресурс]. – Режим доступа: https://docs.microsoft.com/ru-ru/visualstudio/?view=vs-2019 – (Дата обращения – 25.04.2020).
- Коробейников А. Г, Ю.А.Гатчин. Математические основы криптологии. Учебное пособие / СПб: СПб ГУ ИТМО, 2004. – 106 с.
- Коутинхо С. Введение в теорию чисел. Алгоритм RSA / М.: Постчаркет, 2001. – 328 с.
- Мыцко Е. А. Особенности программной реализации вычисления контрольной суммы CRC32 на примере PKZIP, WINZIP, ETHERNET / Е. А. Мыцко, А. Н. Мальчуков // Вестн. науки Сибири. – 2011. – № 1 (1). – с. 279–282.
- Олифер В. Г. Компьютерные сети. Принципы, технологии, протоколы / В. Г. Олифер, Н. А. Олифер. ‒ СПб.: Питер, 2008. ‒ 958 с.
- Темников Ф. Е. Теоретические основы информационной техники: учеб. пособие. – 2-е изд., испр. и доп. / Ф. Е. Темников, В. А. Афонин, В. И. Дмитриев. – М.: Энергия, 1979. – 512 с.
- Яковлев В. В. Оценка влияния помех на производительность протоколов канального уровня / В. В. Яковлев, Ф. И. Кушназаров // Изв. Петерб. гос. ун-та путей сообщения. – СПб.: ПГУПС, 2015. – Вып. 1 (42). – с. 133–138.
- Arthur-Durett K. The Weakness Of Winrar Encrypted Archives To Compression Side-channel Attack, Open Access Theses, Purdue University, 2014
- C# docs [Электронный ресурс]. – Режим доступа: https://docs.microsoft.com/ru-ru/dotnet/csharp/ – (Дата обращения – 19.04.2020).
- Halsall F. Data communications, computer networks and open systems / F. Halsall. – Addison-Wesley: Pearson Education, 1996. ‒ 907 р.
- Hamilton J. Creating ZIP Files with ODS, Division of Research, Kaiser Permanente, Oakland, California, Paper 131-2013, SAS Global Forum 2013
- Ross N. W. A Painless guide to CRC error detection algorithms / N. W. Ross. – 16 Lerwick Avenue, Hazelwood Park, 5066. – Australia, 1993. – URL: http://www.ross.net/crc/download/crc_v3.txt (дата обращения: 18.04.2020).
- Systems Engineering and Software Development Life Cycle Framework [Электронный ресурс]. – Режим доступа: http://opensdlc.org/mediawiki/index.php?title=Main_Page – (Дата обращения – 25.04.2020).
- Tar Vs Zip VsGz: Difference And Efficiency [Электронный ресурс] / URL: https://itsfoss.com/category/linux/ (Дата обращения: 22.04.2020)
- WinRAR Download and Support [Электронный ресурс] / URL: http://www.win-rar.com/rarproducts.html (Дата обращения: 24.04.2020)
- ZIP Format Specification [Электронный ресурс] / URL: http://www.pkware.com/documents/casestudies/APPNOTE.TXT (Дата обращения: 23.04.2020)
Приложение 1. Исходные коды программ
Листинг А1. RSA.cs
using System;
using System.Collections.Generic;
using System.Numerics;
namespace RSAForm
{
public class RSA
{
private char blockSep = ‘*’;
private static Random rnd;
private BigInteger e;
private BigInteger d;
private BigInteger n;
public RSA()
{
this.initParams();
}
public RSA(char blockSep)
{
this.blockSep = blockSep;
this.initParams();
}
private void initParams()
{
rnd = new Random();
int p = 0, q = 0;
generatePQ(out p, out q);
}
private void getPrimeNum(Random rnd, out int n1, out int n2)
{
int firstNumber;
int secondNumber;
do
{
firstNumber = rnd.Next(10000, 20000);
secondNumber = rnd.Next(10000, 20000);
}
while (!Utilities.MillerRabin(firstNumber, 10) || !Utilities.MillerRabin(secondNumber, 10));
n1 = firstNumber;
n2 = secondNumber;
}
private BigInteger NOD(BigInteger a, BigInteger b)
{
while (a != 0 && b != 0)
{
if (a > b)
a %= b;
else
b %= a;
}
return a == 0 ? b : a;
}
// 2. найти модуль
private BigInteger getN(int p, int q)
{
return p * q;
}
// 3. найти значение функции Эйлера fi
private BigInteger getFi(int p, int q)
{
return (p — 1) * (q — 1);
}
// 4. выбрать число е, взаимное простое с fi
private BigInteger getPrime(Random rnd, BigInteger fi)
{
BigInteger e = rnd.Next(1, Math.Abs((int)fi));
do
{
if (NOD(e, fi) == 1)
break;
else e++;
} while (true);
if (e >= fi)
{
e—;
do
{
if (NOD(e, fi) == 1)
break;
else e—;
} while (true);
}
return e;
}
// 5. найти d при помощи расширенного алгоритма Евклида
private BigInteger getD(BigInteger e, BigInteger fi)
{
BigInteger i = fi, v = 0, d = 1;
while (e > 0)
{
BigInteger t = i / e, x = e;
e = i % x;
i = x;
x = d;
d = v — t * x;
v = x;
}
v %= fi;
if (v < 0)
v = (v + fi) % fi;
return v;
}
private string encrypt(int symbol, BigInteger keyE, BigInteger keyN)
{
return BigInteger.ModPow(symbol, keyE, keyN).ToString();
}
private int decrypt(int symbol, BigInteger keyD, BigInteger keyN)
{
return (int)(BigInteger.ModPow(symbol, keyD, keyN));
}
private string textEncrypt(string text, BigInteger e, BigInteger n)
{
string eText = «»;
foreach (var symbol in text)
eText += encrypt(symbol, e, n) + this.blockSep;
return eText;
}
private string textDecrypt(string text, BigInteger d, BigInteger n)
{
string[] arr = text.Split(this.blockSep);
string dText = «»;
foreach (var symbol in arr)
if (symbol != string.Empty)
dText += Convert.ToChar(decrypt(int.Parse(symbol), d, n));
return dText;
}
public string getEncryptedText(string originalText)
{
return textEncrypt(originalText, this.e, this.n);
}
public string getEncryptedText(string originalText, int p, int q)
{
BigInteger fi = getFi(p, q);
this.n = getN(p, q);
this.e = getPrime(rnd, fi);
this.d = getD(e, fi);
Console.WriteLine(«d = {0}, n = {1}», this.d.ToString(), this.n.ToString());
return textEncrypt(originalText, this.e, this.n);
}
public string getDecryptedText(string encryptedText)
{
return textDecrypt(encryptedText, this.d, this.n);
}
public string getDecryptedText(string encryptedText, BigInteger d, BigInteger n)
{
this.d = d;
this.n = n;
return textDecrypt(encryptedText, this.d, this.n);
}
public void generatePQ(out int p, out int q)
{
getPrimeNum(rnd, out q, out p);
BigInteger fi = getFi(p, q);
this.n = getN(p, q);
this.e = getPrime(rnd, fi);
this.d = getD(e, fi);
}
}
}
Листинг А2. Utilities.cs
using System;
using System.Collections.Generic;
using System.Linq;
using System.Numerics;
using System.Text;
namespace RSAForm
{
public class Utilities
{
public static bool MillerRabin(int n, int k)
{
for (int i = 0; i < k; i++) // цикл по количеству раундов
{
// проверка элементарных случаев:
if (n % 2 == 0)
return false;
if (n == 2)
return true;
if (n <= 1)
return false;
// представление n — 1 как 2 ^ s * m
int s = 0;
int m = n — 1;
while (m % 2 == 0)
{
s++;
m = m / 2;
}
// выбор случ. целого числа a в отрезке [2, n − 2]
Random r = new Random();
int a = r.Next(n — 1) + 1;
// поиск mod = a ^ m % n
int temp = m;
long mod = 1;
for (int j = 0; j < temp; j++)
mod = (mod * a) % n;
// вычислить в цикле mod как mod ^ 2 % n
while (temp != n — 1 && mod != 1 && mod != n — 1)
{
mod = (mod * mod) % n;
temp *= 2;
}
// если mod = 1, то составное
// если mod != n — 1, то составное
if (mod != n — 1 && temp % 2 == 0)
return false;
}
return true; // вернуть «вероятно простое»
}
}
}
Листинг А3. Form1.cs
using System;
using System.Windows.Forms;
namespace RSAForm
{
public partial class Form1 : Form
{
RSA rsa;
public Form1()
{
InitializeComponent();
rsa = new RSA();
}
private void TextBox_p_KeyPress(object sender, KeyPressEventArgs e)
{
if (!char.IsControl(e.KeyChar) && !char.IsDigit(e.KeyChar))
{
e.Handled = true;
}
}
private void ButtonEncrypt_Click(object sender, EventArgs e)
{
string plaintext = textBox_plaintext.Text;
int p, q;
if (!generatePQ.Checked)
{
if (!int.TryParse(textBox_p.Text, out p) || !Utilities.MillerRabin(p, 10))
{
MessageBox.Show(«Не удалось считать простое число p!», «Ошибка», MessageBoxButtons.OK, MessageBoxIcon.Error);
return;
}
if (!int.TryParse(textBox_q.Text, out q) || !Utilities.MillerRabin(q, 10))
{
MessageBox.Show(«Не удалось считать простое число q!», «Ошибка», MessageBoxButtons.OK, MessageBoxIcon.Error);
return;
}
textBox_ciphertext.Text = rsa.getEncryptedText(plaintext, p, q);
}
else
{
rsa.generatePQ(out p, out q);
textBox_p.Text = p.ToString();
textBox_q.Text = q.ToString();
textBox_ciphertext.Text = rsa.getEncryptedText(plaintext);
}
sameDecipherButton.Enabled = true;
}
private void ButtonDecipher_Click(object sender, EventArgs e)
{
string cipherText = textBox_ciphertext.Text;
int d, n;
if (!int.TryParse(textBox_d.Text, out d))
{
MessageBox.Show(«Не удалось считать число d!», «Ошибка», MessageBoxButtons.OK, MessageBoxIcon.Error);
return;
}
if (!int.TryParse(textBox_n.Text, out n))
{
MessageBox.Show(«Не удалось считать число n!», «Ошибка», MessageBoxButtons.OK, MessageBoxIcon.Error);
return;
}
textBox_plaintext.Text = rsa.getDecryptedText(cipherText, d, n);
}
private void SameDecipherButton_Click(object sender, EventArgs e)
{
string cipherText = textBox_ciphertext.Text;
textBox_plaintext.Text = rsa.getDecryptedText(cipherText);
sameDecipherButton.Enabled = false;
}
private void TextBox_ciphertext_TextChanged(object sender, EventArgs e)
{
sameDecipherButton.Enabled = false;
}
}
}
Листинг B1. Form1.cs
using System;
using System.Collections.Generic;
using System.Drawing;
using System.IO;
using System.Windows.Forms;
namespace CRC32List
{
public partial class FormMain : Form
{
List<string> files = new List<string>(); // список имен файлов
string folder = null; // директория с файлами
int mouseWindowX = 0;
int mouseWindowY = 0;
public FormMain()
{
InitializeComponent();
}
// открытие файла(-ов):
private void button1_Click(object sender, EventArgs e)
{
// выбор начальной директории:
if (folder != null)
{
if (Directory.Exists(folder))
openFileDialog1.InitialDirectory = folder;
}
else
openFileDialog1.InitialDirectory = Environment.GetFolderPath(Environment.SpecialFolder.Desktop);
// открытие файлов при помощи файлового диалога:
DialogResult result = openFileDialog1.ShowDialog();
if (result == DialogResult.OK)
{
folder = Path.GetDirectoryName(openFileDialog1.FileName);
listView2.Items.Clear();
files.Clear();
files.AddRange(openFileDialog1.FileNames);
funcGet();
}
}
// получение списка контрольных сумм и добавление его на форму рядом со списком файлов:
private void funcGet()
{
int count = 0;
foreach (string file in files)
if (File.Exists(file))
{
string[] row = { Path.GetFileName(file), getCRC(file) };
var listViewItem = new ListViewItem(row);
listView2.Items.Add(listViewItem);
count++;
}
filesName.Text = «Файлы (» + count.ToString() + «):»;
}
// получение контрольной суммы для переданного файла:
private string getCRC(string file)
{
FileStream streamFile = File.OpenRead(file);
string record = string.Format(«{0:X}», calculateCRC(streamFile));
streamFile.Close();
while (record.Length != 8)
record = «0» + record;
return record;
}
// вычисление контрольной суммы:
private uint calculateCRC(Stream stream)
{
const int buffer_size = 1024;
const uint POLYNOMIAL = 0xEDB88320;
uint result = 0xFFFFFFFF;
uint Crc32;
byte[] buffer = new byte[buffer_size];
uint[] table_CRC32 = new uint[256];
unchecked
{
for (int i = 0; i < 256; i++)
{
Crc32 = (uint)i;
for (int j = 8; j > 0; j—)
if ((Crc32 & 1) == 1)
Crc32 = (Crc32 >> 1) ^ POLYNOMIAL;
else
Crc32 >>= 1;
table_CRC32[i] = Crc32;
}
int count = stream.Read(buffer, 0, buffer_size);
while (count > 0)
{
for (int i = 0; i < count; i++)
result = ((result) >> 8) ^ table_CRC32[(buffer[i]) ^ ((result) & 0x000000FF)];
count = stream.Read(buffer, 0, buffer_size);
}
}
stream.Close();
return ~result;
}
private void listView2_DragDrop(object sender, DragEventArgs e)
{
listView2.Items.Clear();
files.Clear();
files.AddRange((string[])e.Data.GetData(DataFormats.FileDrop));
funcGet();
}
private void listView2_DragEnter(object sender, DragEventArgs e)
{
if (e.Data.GetDataPresent(DataFormats.FileDrop, false))
e.Effect = DragDropEffects.All;
}
private void button2_Click(object sender, EventArgs e)
{
Application.Exit();
}
private void pictureBox1_MouseDown(object sender, MouseEventArgs e)
{
mouseWindowX = e.X + 147;
mouseWindowY = e.Y + 344;
pictureBox1.MouseMove += pictureBox1_MouseMove;
}
private void pictureBox1_MouseMove(object sender, MouseEventArgs e)
{
Location = new Point(Cursor.Position.X — mouseWindowX, Cursor.Position.Y — mouseWindowY);
}
private void pictureBox1_MouseUp(object sender, MouseEventArgs e)
{
pictureBox1.MouseMove -= pictureBox1_MouseMove;
}
}
}
- Процессы принятия решений в организации ООО «Компания «Омская Недвижимость»
- Основы работы с операционной системой Windows 7.(История ОС Windows. Семейства 4)
- Интеллектуальная собственность как объект правовой охраны
- Организационное проектирование
- Моделирование предметной области «Управление домашними финансами» с помощью UML
- Основы алгоритмизации и программирования (рассмотрение критериев выбора средств разработки)
- Основные понятия объектно-ориентированного программирования
- Роль мотивации в поведении организации АО ’’Концерн ”НПО ”Аврора”
- Потребительские свойства и показатели качества товаров (Расчет комплексных показателей)
- Коммерческая деятельность розничного торгового предприятия и ее совершенствование (на примере конкретной организации)
- Функция менеджмента (ЗАО «Ваша мебель»)
- Кадровая стратегия в системе стратегического управления организацией (ООО «СЕРВИС»)
Каждый из нас знает такое слово как «шифрование». Шифрование входит в состав криптографии. Криптографии уже более 4-х тысяч лет. Она появилась впервые в Древнем Египте. Имеются свидетельства, что криптография как техника защиты текста возникла вместе с письменностью, и способы тайного письма были известны уже древним цивилизациям Индии, Египта и Месопотамии.
СОДЕРЖАНИЕ
Введение……………………………………………………………………… 3
Глава 1 Шифрование с закрытым ключом………………………………… 4
1.1 Определение……………………………………………………………… 5
1.2 Закрытый ключ…………………………………………………………… 6
1.3 Примеры использования закрытого ключа…………………………….. 6
1.4 Ключевые носители……………………………………………………… 7
1.5 Генерация закрытого ключа…………………………………………….. 8
1.6 Преимущества использования смарт-карты……………………………. 8
1.7 Научная основа шифрования с закрытым ключом…………………… 10
1.8 Основные принципы шифрования с закрытым ключом………………. 10
1.9 Преимущество использования шифрования с закрытым ключом…….. 10
1.10 Вывод……………………………………………………………………. 11
Глава 2 Шифрование с закрытым ключом в нашей жизни……………….. 12
2.1 Ключевая особенность…………………………………………………… 13
2.2 Использование шифрования в Windows……………………………….. 15
2.3 Социальные сети и шифрование с закрытым ключом…………………. 15
2.4 Шифрование с закрытым ключом на Интернет сайтах……………… 16
2.5 Принцип работы закрытого ключа в Веб сайтах………………………. 17
Заключение…………………………………………………………………… 19
Список используемой литературы …………………………………………. 20
ВВЕДЕНИЕ
Каждый из нас знает такое слово как «шифрование». Шифрование входит в состав криптографии. Криптографии уже более 4-х тысяч лет. Она появилась впервые в Древнем Египте. Имеются свидетельства, что криптография как техника защиты текста возникла вместе с письменностью, и способы тайного письма были известны уже древним цивилизациям Индии, Египта и Месопотамии. В древнеиндийских текстах среди 64 искусств названы способы изменения текста, некоторые из них можно отнести к криптографическим.
Сегодня, в век цифровых технологий, каждый из нас сталкивается с шифрованием даже не замечая этого. Мы ежедневно пользуемся разными Интернет-ресурсами, которые зашифровывают данные для того, чтобы избежать получения этих данных третьими лицами. Набирая текст в поисковой строке, поисковик шифрует доступные ему данные. В наш век очень ценна информация. Вряд ли Вы хотите, чтобы Ваше сообщение прочитал кто-то другой, а не получатель. Многие передают в сообщениях очень много конфиденциальной и ценной информации. Как раз, чтобы эта информация не попала злоумышленнику, большинство сервисов обмена сообщений поддерживают шифрование. А самые безопасные— шифрование с закрытым ключом. Было издано много технической литературы на эту тему, а также много материалов в Интернете. Все вышесказанное предопределяет актуальность этой темы.
Я ставлю перед собой задачу: раскрыть тему шифрования с закрытым ключом, рассказать принципы работы и области применения. Для достижения моей цели я буду использовать свои личные знания и опыт, материал из технической литературы и, конечно, материалы из Интернета.
Я выбрал эту тему, потому что она мне была интересно и сейчас очень актуальна. Это именно та тема, про которую слышали все, но всего лишь часть знает принцип её работы.
Нужна помощь в написании курсовой?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Подробнее
Глава 1. Шифрование с закрытым ключом
1.1. Определение
Существует несколько методов шифрования, которые различны в принципах взаимодействиях и методах работы. Это симметричное шифрование, при котором для шифрования и расшифровывания используется один и тот же ключ. Отсюда название — симметричные. Алгоритм и ключ выбирается заранее и известен обеим сторонам. Сохранение ключа в секретности является важной задачей для установления и поддержки защищённого канала связи. В связи с этим, возникает проблема начальной передачи ключа (синхронизации ключей). И второй —асимметричное шифрование или шифрование с закрытым ключом, в котором используются два ключа — открытый и закрытый, связанные определённым математическим образом друг с другом. Открытый ключ передаётся по открытому (то есть незащищённому, доступному для наблюдения) каналу и используется для шифрования сообщения и для проверки ЭЦП. Для расшифровки сообщения и для генерации ЭЦП используется секретный ключ.Данная схема решает проблему симметричных схем, связанную с начальной передачей ключа другой стороне. Если в симметричных схемах злоумышленник перехватит ключ, то он сможет как «слушать», так и вносить правки в передаваемую информацию. В асимметричных системах другой стороне передается открытый ключ, который позволяет шифровать, но не расшифровывать информацию.
Если подробнее, то шифрование с закрытым ключом(разновидность асимметричного шифрования, асимметричного шифра) — система шифрования и/или электронной подписи (ЭП), при которой открытый ключ передаётся по открытому (то есть незащищённому, доступному для наблюдения) каналу и используется для проверки ЭП и для шифрования сообщения. Для генерации ЭП и для расшифровки сообщения используется закрытый ключ. Криптографические системы с открытым ключом в настоящее время широко применяются в различных сетевых протоколах, в частности, в протоколах TLS и его предшественнике SSL (лежащих в основе HTTPS), в SSH. Также используется в PGP, S/MIME.
Таким образом решается проблема симметричных систем, связанная с синхронизацией ключей. Первыми исследователями, которые изобрели и раскрыли понятие шифрования с открытым кодом, были УитфилдДиффи и Мартин Хеллман из Стэнфордского университета и Ральф Меркле из Калифорнийского университета в Беркли. В 1976 году их работа «Новые направления в современной криптографии» открыла новую область в криптографии, теперь известную как криптография с открытым ключом.
1.2 Закрытый ключ
1.3 Примеры использования закрытого ключа
Существует несколько методов использования закрытого ключа. Один из них — электронная подпись. При которой закрытый ключ применяется при вычислении электронной цифровой подписи (ЭП). При проверке ЭП применяется открытый ключ, соответствующий использованному при вычислении ЭЦП закрытому ключу. При условии использования стойкого алгоритма цифровой подписи без обладания закрытым ключом нельзя подделать цифровую подпись. Второй — шифрование сообщений. При использовании этого метода применяется открытый ключ, соответствующий закрытому ключу получателя шифрограммы. При расшифровке сообщения получатель использует свой закрытый ключ. Если применяется стойкий асимметричный шифр, без обладания закрытым ключом нельзя прочесть шифрограмму.
Нужна помощь в написании курсовой?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Заказать курсовую
1.4 Ключевые носители
Сохранение закрытого ключа в тайне — важнейшее условие его безопасного использования. Наилучшим способом хранения электронного закрытого ключа является использование носителя, с которого закрытый ключ невозможно скопировать. К таким носителям относятся смарт-карты и их аналоги, а также устройства HardwareSecurityModule (HSM).
1.5 Генерация закрытого ключа
Помимо применения надёжных шифров и ключевых носителей, важным условием обеспечения безопасности при использовании закрытого ключа является его непредсказуемость, которая достигается путём использования качественных датчиков случайных чисел. Как правило, смарт-карты и HSM содержат в себе качественные датчики случайных чисел и механизмы, позволяющие осуществлять асимметричные криптографические преобразования. Благодаря этому закрытый ключ может генерироваться и использоваться только внутри смарт-карты или HSM.
1.6 Преимущества использования смарт-карты
Преимуществом использования таких аппаратных средств, как смарт-карты и HSM, для генерации и применения закрытого ключа является то, что при условии надёжности этих средств и неприменения высоко-технологического аппаратного взлома обеспечивается 100%-ная гарантия сохранения закрытого ключа в тайне. Недостатком же является то, что утрата или поломка смарт-карты или HSM ведёт к безвозвратной потере закрытого ключа и невозможности расшифровать сообщения, зашифрованные с использованием открытого ключа, соответствующего утраченному закрытому ключу.
1.7 Научная основа шифрования с закрытым ключом
Начало асимметричным шифрам было положено в работе «Новые направления в современной криптографии» УитфилдаДиффи и Мартина Хеллмана, опубликованной в 1976 году. Находясь под влиянием работы Ральфа Меркла о распространении открытого ключа, они предложили метод получения секретных ключей, используя открытый канал. Этот метод экспоненциального обмена ключей, который стал известен как обмен ключами Диффи — Хеллмана, был первым опубликованным практичным методом для установления разделения секретного ключа между заверенными пользователями канала. В 2002 году Хеллман предложил называть данный алгоритм «Диффи — Хеллмана — Меркле», признавая вклад Меркле в изобретение криптографии с открытым ключом. Эта же схема была разработана МалькольмомВильямсоном(англ. Malcolm J. Williamson) в 1970-х, но держалась в секрете до 1997 года. Метод Меркле по распространению открытого ключа был изобретён в 1974 и опубликован в 1978 году, его также называют загадкой Меркле.
В 1977 году учёными Рональдом Ривестом, Ади Шамиром и Леонардом Адлеманом из Массачусетского технологического института был разработан алгоритм шифрования, основанный на проблеме о разложении на множители. Система была названа по первым буквам их фамилий (RSA — Rivest, Shamir, Adleman). Эта же система была изобретена в 1973 году Клиффордом Коксом (англ. CliffordCocks), работавшим в центре правительственной связи (GCHQ), но эта работа хранилась лишь во внутренних документах центра, поэтому о её существовании не было известно до 1977 года. RSA стал первым алгоритмом, пригодным и для шифрования, и для цифровой подписи.
Вообще, в основу известных асимметричных криптосистем кладётся одна из сложных математических проблем, которая позволяет строить односторонние функции и функции-лазейки. Например, криптосистемы Меркля — Хеллмана и Хора — Ривеста опираются на так называемую задачу об укладке рюкзака.
1.8 Основные принципы работы шифрования с закрытым ключом
Нужна помощь в написании курсовой?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Подробнее
1. Начинаем с трудной задачи P{displaystyle P}. Она должна решаться сложно в смысле теории: не должно быть алгоритма, с помощью которого можно было бы перебрать все варианты решения задачи P {displaystyle P} за полиномиальное время относительно размера задачи. Более правильно сказать: не должно быть известного полиномиального алгоритма, решающего данную задачу — так как ни для одной задачи ещё пока не доказано, что для неё подходящего алгоритма нет в принципе.
2. Можно выделить легкую подзадачу {displaystyle P’}P1 из {displaystyle P}P. Она должна решаться за полиномиальное время и лучше, если за линейное.
3. «Перетасовываем и взбалтываем» {displaystyle P’}P1, чтобы получить задачу P2 {displaystyle P»}, совершенно не похожую на первоначальную. Задача {displaystyle P»}P2 должна по крайней мере выглядеть как оригинальная труднорешаемая задача P {displaystyle P}.
4. P2 открывается с описанием, как она может быть использована в роли ключа зашифрования. Как из {displaystyle P»}P2 получить P1 {displaystyle P’}, держится в секрете как секретная лазейка.
5. Криптосистема организована так, что алгоритмы расшифрования для легального пользователя и криптоаналитика существенно различны. В то время как второй решаетP2 {displaystyle P»}-задачу, первый использует секретную лазейку и решает {displaystyle P’}P1задачу.
1.9 Преимущества использования шифрования с закрытым ключом
· Не нужно предварительно передавать секретный ключ по надёжному каналу;
· только одной стороне известен ключ дешифрования, который нужно держать в секрете (в симметричной криптографии такой ключ известен обеим сторонам и должен держаться в секрете обеими);
· в больших сетях число ключей в асимметричной криптосистеме значительно меньше, чем в симметричной.
Нужна помощь в написании курсовой?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Заказать курсовую
1.10 Недостатки использования шифрования с закрытым ключом
· в алгоритм сложнее внести изменения;
· более длинные ключи — ниже приведена таблица, сопоставляющая длину ключа симметричного алгоритма с длиной ключа RSA с аналогичной криптостойкостью.
1.11 История
Криптография прошлых веков имела одну огромную проблему — проблема передачи ключей. В те времена существовали только так называемые «симметричные» шифры — шифры при котором данные шифруются и расшифровываются одним и тем же ключом.
К примеру, Алиса зашифровала некоторое сообщение и хочет отправить его Бобу. Естественно, чтобы Боб его прочитал, ему нужен ключ которым было зашифровано данное сообщение. И тут возникает проблема, как передать ключ чтобы его никто не смог перехватить. Пытливые умы предложат — пусть передают при личной встрече, а потом общаются сколько захотят. Да, не спорю, выход. А теперь представьте на секунду, что ваша интернет почта, перед тем как вы авторизируетесь в ней, потребует вашей поездки до физического местоположения сервера с почтой. Удобно? Пожалуй не очень.
Конечно ключ можно передавать по другому каналу связи. Но криптография рассматривает все незащищенные каналы связи как небезопасные. То есть передача ключа Бобу по телефону, например, считается небезопасной так, как ничто не мешает Еве прослушивать и телефон в том числе.
До 70-ых годов, эта проблема настолько стала привычной, что считался аксиомой тот факт, что для передачи сообщения нужно передавать и ключ которым сообщение зашифровано (причем некоторых люди до сих пор считают именно так). Но в 76 году Диффи и Хеллман предложили свой «метод экспоненциального обмена ключей». С этих годов и началось развитие асимметричных криптосистем.
Нужна помощь в написании курсовой?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Заказать курсовую
1.12 Вывод
Таким образом, стало ясно, что шифрование с закрытым ключом используется повсеместно. Существует несколько технологий использования шифрования с закрытым ключом, каждый из которых имеет свои плюсы и минусы. Каждый из методов шифрования имеет разные принципы. Многие из названных выше технологий активно используются и сейчас. Действительно, закрытый ключ активно используется в большинстве самых популярных сервисов. Криптография прошлых веков имела одну огромную проблему — проблема передачи ключей. В те времена существовали только так называемые «симметричные» шифры — шифры при котором данные шифруются и расшифровываются одним и тем же ключом.Преимуществом использования таких аппаратных средств, как смарт-карты и HSM, для генерации и применения закрытого ключа является то, что при условии надёжности этих средств и неприменения высоко-технологического аппаратного взлома обеспечивается 100%-ная гарантия сохранения закрытого ключа в тайне.
Глава 2. Шифрование с закрытым ключом в нашей жизни
2.1Ключевая особенность
Долгое время традиционная криптография использовала шифрование стайным или симметричным ключом — один и тот же ключ использовался как для зашифровывания, так и для расшифровки (дешифрования) данных.Наглядно это можно представить в виде замка, которым запирался сундук с тайным сообщением. Пара одинаковых ключей к этому замку была как у отправителя сообщения (шифровальщика), так и у получателя (дешифровальщика).Разумеется, в действительности никто не отправлял сообщения в запертых сундуках. Тексты, которые надо было зашифровать, особым образом видоизменялись с использованием тайногоключа (шифра) — последовательностисимволов, которая смешиваясь с передаваемым сообщением особым образом (называемым алгоритмом шифрования), приводила к получению шифровки (шифротекста) — сообщения, которое невозможно было прочитать, не зная алгоритма и шифра (ключа).
2.2Визуальное представление
Представим себе навесной замок с двумя замочными скважинами и двумя ключами левый ключ через левую замочную скважину может снимать фиксацию с левой половинки дуги замка, освобождая ее и открывая весь замок. Правый ключ через правую замочную скважину может фиксировать правую половинку дуги в замке, тем самым закрывая замок. Но, после закрытия, этот ключ не может уже освободить от фиксации правую часть дуги и тем самым открыть замок.
Первоначально замок с зафиксированной левой половинкой дуги ирасфиксированной правой , а также с ключом 2 (открытым) доставляется лицу, которое должно отправить тайное послание.
Получив замок и открытый ключ , отправитель навешивает его на сундук с тайным посланием и запирает его полученным ключом 2. Теперь сундук закрыт и даже отправитель не может его открыть, поскольку его ключ может только зафиксировать правую часть дуги в замке, но не может освободить от фиксации.
Получатель открывает замок ключом и тайное послание прочитано!
Нужна помощь в написании курсовой?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена курсовой
Пользуясь терминологией ассиметричной криптографии с открытым ключом, ключ 1 — это закрытый (приватный) ключ, а ключ 2 — это открытый (публичный) ключ.
2.3 Использование шифрования в Windows
PGP (от англ. PrettyGoodPrivacy) означает «вполне хорошая приватность». На самом деле это очень хорошая приватность. При правильном использовании PGP может защитить содержимое ваших сообщений, текстов и даже файлов от самых серьезных правительственных средств слежки. Когда Эдвард Сноуден говорил «шифрованиеработает», он подразумевал именно PGP и связанные с ней программы.
К сожалению, PGP – не самый лёгкий для освоения и использования инструмент. Стойкое шифрование, реализованное в PGP (шифрование с открытым ключом) – мощное, но довольно мудрёное средство защиты. Сама программа PGP существует с 1991 года и является ровесником самых первых версий MicrosoftWindows. С тех давних пор внешний вид PGP не особенно изменился.
2.4Социальные сети и шифрование с закрытым ключом
Многие социальные сети используют эту технологию шифрования.
Используют из-за ряда причин, названных выше. Это, действительно, безопасно. Такие социальные сети гиганты, как ВКонтакте, Facebook, Twitter и др. используют шифрование с закрытым ключом. При каждом отправленном сообщении, оно шифруется с закрытым ключом, по технологии описанным выше и отправляется на сервер, Вы, как получатель, получаете зашифрованное сообщение, а на Вашем устройстве оно уже расшифровывается.
2.5Шифрование с закрытым ключом наИнтернет сайтах.
Нужна помощь в написании курсовой?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Подробнее
Основной целью применения SSL сертификатов является шифрование данных, передаваемых на сервер от клиента и клиенту от сервера. Для обеспечения безопасности такого соединения современные браузеры используют алгоритм TLS, основанный на сертификатах формата X.509. Данный алгоритм применяет ассиметричное шифрование, чтобы создать ключ сессии для симмертичного шифрования. Последнее используется непосредственно для передачи данных после установления защищенного соединения.
2.6Принцип работы закрытого ключа в Веб-сайтах
В ассиметричном шифровании применяется пара ключей: открытый (Publickey) и закрытый, также называемый секретным (Privatekey). Открытый и закрытый ключи в данном случае позволяют криптографическому алгоритму шифровать и дешифровать сообщение. При этом сообщения, зашифрованные открытым ключом, расшифровать можно только с помощью закрытого ключа. Открытый ключ публикуется в сертификате владельца и доступен подключившемуся клиенту, а закрытый – хранится у владельца сертификата.
Открытый и закрытый ключ между собой связаны математическими зависимостями, поэтому подобрать открытый или закрытый ключ невозможно за короткое время (срок действия сертификата). Именно поэтому максимальный срок действия SSL сертификатов более высого уровня защиты всегда ниже. Так, сертификаты EV можно заказать максимум на 2 года. При этом заказывая новый SSL сертификат или продлевая старый, важно генерировать новый CSR запрос, так как к нему привязывается Ваш закрытый ключ и при выпуске нового SSL сертификата лучше его обновлять.
Взаимодействие клиента с сервером происходит следующим образом:
1. Браузер на основе открытого ключа шифрует запрос и отправляет его на сервер;
2. сервер, применяя закрытый ключ, расшифровывает полученное сообщение;
3. сервер шифрует закрытым ключом свой цифровой идентификатор и передает его клиенту;
4. клиент сверяет идентификатор сервера и передает свой;
Нужна помощь в написании курсовой?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Подробнее
5. после взаимной аутентификации клиент шифрует открытым ключом ключ будущей сессии и передает его на сервер;
6. все последующие сообщения, которые передаются между клиентом и сервером, подписываются ключом сессии и шифруются с использованием открытого и закрытого ключа.
Таким образом обеспечиваются несколько пунктов безопасности:
§ исключается возможность утечки информации – при перехвате её нельзя будет расшифровать;
§ сервер подтверждает свой адрес и идентификатор, отсекается возможность перенаправления на другой сайт (фишинг);
§ клиенту присваивается индивидуальная сессия, что позволяет отличать его от других клиентов более надежно;
§ после установки защищенной сессии все сообщения шифруются с использованием идентификатора клиента, и не могут быть незаметно перехвачены или изменены.
В общем случае шифрование открытым и закрытым ключом можно рассматривать как кейс, для которого используются два ключа: одним можно только закрыть, другим – открыть. Если кейс закрыли первым ключом, открыть его может только второй, если закрыли вторым, чтобы открыть – потребуется первый.
Нужна помощь в написании курсовой?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена курсовой
2.7Пошаговое примененияRSA шифрования
2.6.1 Шаг первый. Подготовка ключей
Я должен проделать предварительные действия: сгенерировать публичный и приватный ключ.
· Выбираю два простых числа. Пусть это будет p=3 и q=7.
· Вычисляем модуль — произведение наших p и q: n=p×q=3×7=21.
· Вычисляем функцию Эйлера: φ=(p-1)×(q-1)=2×6=12.
Теперь пара чисел {e, n} — это мой открытый ключ. Я отправляю его вам, чтобы вы зашифровали своё сообщение. Но для меня это ещё не всё. Я должен получить закрытый ключ.
Мне нужно вычислить число d, обратное е по модулю φ. То есть остаток от деления по модулю φ произведения d×e должен быть равен 1. Запишем это в обозначениях, принятых во многих языках программирования: (d×е)%φ=1. Или (d×5)%12=1. d может быть равно 5 ((5×5)%12=25%12=1), но чтобы оно не путалось с e в дальнейшем повествовании, давайте возьмём его равным 17. Можете проверить сами, что (17×5)%12 действительно равно 1 (17×5-12×7=1). Итак d=17. Пара {d, n} — это секретный ключ, его я оставляю у себя. Его нельзя сообщать никому. Только обладатель секретного ключа может расшифровать то, что было зашифровано открытым ключом.
Нужна помощь в написании курсовой?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Подробнее
2.6.2 Шаг второй. Шифрование
Теперь пришла ваша очередь шифровать ваше сообщение. Допустим, ваше сообщение это число 19. Обозначим его P=19. Кроме него у вас уже есть мой открытый ключ: {e, n} = {5, 21}. Шифрование выполняется по следующему алгоритму:
· Возводите ваше сообщение в степень e по модулю n. То есть, вычисляете 19 в степени 5 (2476099) и берёте остаток от деления на 21. Получается 10 — это ваши закодированные данные.
Строго говоря, вам вовсе незачем вычислять огромное число «19 в степени 5». При каждом умножении достаточно вычислять не полное произведение, а только остаток от деления на 21. Но это уже детали реализации вычислений, давайте не будем в них углубляться.
Полученные данные E=10, вы отправляете мне.
Здесь надо заметить, что сообщение P=19 не должно быть больше n=21. иначе ничего не получится.
2.6.3. Шаг третий. Расшифровка
Я получил ваши данные (E=10), и у меня имеется закрытый ключ {d, n} = {17, 21}.
Нужна помощь в написании курсовой?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Подробнее
Обратите внимание на то, что открытый ключ не может расшифровать сообщение. А закрытый ключ я никому не говорил. В этом вся прелесть асимметричного шифрования.
Начинаем раскодировать:
· Я делаю операцию, очень похожую на вашу, но вместо e использую d. Возвожу E в степень d: получаю 10 в степень 17 (позвольте, я не буду писать единичку с семнадцатью нулями). Вычисляю остаток от деления на 21 и получаю 19 — ваше сообщение.
Заметьте, никто, кроме меня (даже вы!) не может расшифровать ваше сообщение (E=10), так как ни у кого нет закрытого ключа.
2.6.4 В чём гарантия надёжности шифрования?
Надёжность шифрования обеспечивается тем, что третьему лицу (старающемуся взломать шифр) очень трудно вычислить закрытый ключ по открытому. Оба ключа вычисляются из одной пары простых чисел (p и q). То есть ключи связаны между собой. Но установить эту связь очень сложно. Основной загвоздкой является декомпозиция модуля n на простые сомножители p и q. Если число является произведением двух очень больших простых чисел, то его очень трудно разложить на множители.
Постараюсь это показать на примере. Давайте разложим на множители число 360:
· сразу ясно. что оно делится на два (получили 2)
Нужна помощь в написании курсовой?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Подробнее
· оставшееся 180 тоже, очевидно чётное (ещё 2)
· 90 — тоже чётное (ещё двойка)
· 45 не делится на 2, но следующая же попытка оказывается успешной — оно делится на три (получили 3)
· 15 тоже делится на 3
· 5 — простое.
Мы на каждом шагу, практически без перебора, получали всё новые и новые множители, легко получив полное разложение 360=2×2×2×3×3×5
Давайте теперь возьмём число 361. Тут нам придётся помучиться.
· оно не чётное
Нужна помощь в написании курсовой?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена курсовой
· три — нет, не делится
· пять (допустим, мы поступаем умно и перебираем только простые числа, хотя, на практике, поиск больших простых чисел, сам по себе, является сложной задачей) — не подходит
· семь? — нет.
· …
· и только 19 даст нам ответ: 361=19×19.
При использовании больших чисел, задача становится очень сложной. Это позволяет надеяться, что у взломщика просто не хватит вычислительных ресурсов, чтобы сломать ваши шифр за обозримое время.
2.6.5 А как это всё работает на практике?
Давайте рассмотрим чуть более приближенный к жизни пример. Зашифруем и расшифруем слово «КРОТ», предложенное одним из читателей. А заодно, бегло рассмотрим, какие проблемы при этом встречаются и как они решаются.
Нужна помощь в написании курсовой?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Подробнее
Сперва сгенерируем ключи с чуть большими числами. Они не так наглядны, но позволят нам шифровать не только числа от нуля до 20.
Оттолкнёмся от пары простых чисел {p, q} = {17, 19}. Пусть наш открытый ключ будет {e, n} = {5, 323}, а закрытый {d, n} = {173, 323}.
Мы готовы к шифрованию. Переведём наше слово в цифровое представление. Мы можем взять просто номера букв в алфавите. У нас получится последовательность чисел: 11, 17, 15, 19.
Мы можем зашифровать каждое из этих чисел открытым ключом {e, n} = {5, 323} и получить шифровку 197, 272, 2, 304. Эти числа можно передать получателю, обладающему закрытым ключом {d, n} = {173, 323} и он всё расшифрует.
2.6.6 Сложности использования
На самом деле, изложенный способ шифрования очень слаб и никогда не используется. Причина проста — шифрование по буквам. Одна и та же буква будет шифроваться одним и тем же числом. Если злоумышленник перехватит достаточно большое сообщение, он сможет догадаться о его содержимом. Сперва он обратит внимание на частые коды пробелов и разделит шифровку на слова. Потом он заметит однобуквенные слова и догадается, как кодируются буквы «a», «и», «o», «в», «к»… Путём недолгого перебора, он вычислит дополнительные буквы по коротким словам, типа «но», «не», «по». И по более длинным словам без труда восстановит все оставшиеся буквы.
Таким образом, злоумышленнику не придётся отгадывать ваши секретные ключи. Он взломает ваше сообщение, не зная их.
Чтобы этого не происходило, используются специальные дополнительные алгоритмы, суть которых в том, что каждая предыдущая часть сообщения начинает влиять на следующую.
Нужна помощь в написании курсовой?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Заказать курсовую
Упрощённо, это выглядит так. Перед шифрованием, мы применяем к сообщению правило: b := (b + a) % n. Где a — предыдущая часть сообщения, а b — следующая. То есть наше сообщение (11, 17, 15, 19) изменяется. 11 остаётся без изменений. 17 превращается в (11 + 17) % 323 = 28. 15 становится (15 + 28) % 323 = 43. A 19 превращается в 62.
Последовательность (11, 28, 43, 62) получается «запутанной». Все буквы в ней как бы перемешаны, в том смысле, что на каждый код влияет не одна буква, а все предыдущие.
Тот, кто получит ваше сообщение, должен будет проделать обратную операцию, со знаком «минус»: b := (b - a) % n. И только тогда он получит коды букв.
На практике, в исходное сообщение специально добавляются случайные и бессмысленные буквы в начало. Чтобы даже по первому коду было невозможно ничего понять. Получатель просто отбрасывает начало сообщения.
То есть мы можем добавить случайное число в начало и получить (299, 11, 17, 15, 19). После перемешивания получится: 299, 310, 4, 19, 38. После шифрования уже невозможно будет догадаться где была какая буква.
В реальной жизни всё ещё немного сложнее. Блоки, на которые бьётся сообщение длиннее одной буквы. Поэтому, сперва применяются алгоритмы выравнивания, потом алгоритмы разбиения на блоки с перепутыванием, и только
ЗАКЛЮЧЕНИЕ
Я рассмотрел все возможные варианты шифрования с закрытым ключом и вывел их все. Таким образом, злоумышленнику не придётся отгадывать ваши секретные ключи. Он взломает ваше сообщение, не зная их.
Нужна помощь в написании курсовой?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Подробнее
Чтобы этого не происходило, используются специальные дополнительные алгоритмы, суть которых в том, что каждая предыдущая часть сообщения начинает влиять на следующую. Сегодня, в век цифровых технологий, каждый из нас сталкивается с шифрованием даже не замечая этого. Мы ежедневно пользуемся разными Интернет-ресурсами, которые зашифровывают данные для того, чтобы избежать получения этих данных третьими лицами. Набирая текст в поисковой строке, поисковик шифрует доступные ему данные. Когда вы заходите на любой сайт в интернете, информация о Вашем устройстве, IP адресе, MAC адресе и идентификатор сессии так же шифруется. Многие люди не интересуются этой темой и для кого-то это покажется слишком сложным. Действительно, отправляя сообщение своему другу в мессенджере, мы не хотим знать каким образом он его получает, нам важно, чтобы он его получил. В наш век очень ценна информация. Вряд ли Вы хотите, чтобы Ваше сообщение прочитал кто-то другой, а не получатель. Многие передают в сообщениях очень много конфиденциальной и ценной информации. Как раз, чтобы эта информация не попала злоумышленнику, большинство сервисов обмена сообщений поддерживают шифрование. А самые безопасные — шифрование с закрытым ключом. Было издано много технической литературы на эту тему, а также много материалов в Интернете. Все вышесказанное предопределяет актуальность этой темы.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
Книги:
1. Саломаа А. Криптография с открытым ключом. — М.: Мир, 1995. — 318 с. — ISBN 5-03-001991-X.
A. J. Menezes, P. C. van Oorschot, S. A. Vanstone. Handbook of Applied Cryptography. — 1997. — ISBN 0-8493-8523-7.
2. Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си = AppliedCryptography. Protocols, Algorithms and Source Code in C. — М.: Триумф, 2002. — 816 с. — 3000 экз. — ISBN 5-89392-055-4.
3. Э. Мэйволд. Безопасность сетей. — 2006. — 528 с. — ISBN 978-5-9570-0046-9.
4. Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си = AppliedCryptography. Protocols, Algorithms and Source Code in C / Подред. А. Б. Васильева. — М.: Триумф, 2002. — 816 с. — ISBN 5-89392-055-4.
Интернет-ресурсы:
1. https://ru.wikipedia.org/wiki/История_криптографии
2. https://ru.wikipedia.org/wiki/Шифрование
Нужна помощь в написании курсовой?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Подробнее
3. https://ru.wikipedia.org/wiki/Закрытый_ключ
4. https://ru.wikipedia.org/wiki/Криптосистема_с_открытым_ключом
5. https://medium.com/bitcoin-review/шифрование-с-открытым-ключом-наглядная-иллюстрация-fbea974f5896
6.https://ssd.eff.org/ru/module/введение-в-шифрование-с-открытым-ключом-и-pgp
7. https://www.emaro-ssl.ru/blog/public-and-private-key/
8. https://intsystem.org/security/asymmetric-encryption-how-it-work/
9. http://www.michurin.net/computer-science/rsa.html
10. http://www.sql.ru/forum/494305/shifrovanie-zakrytym-kluchom-v-net











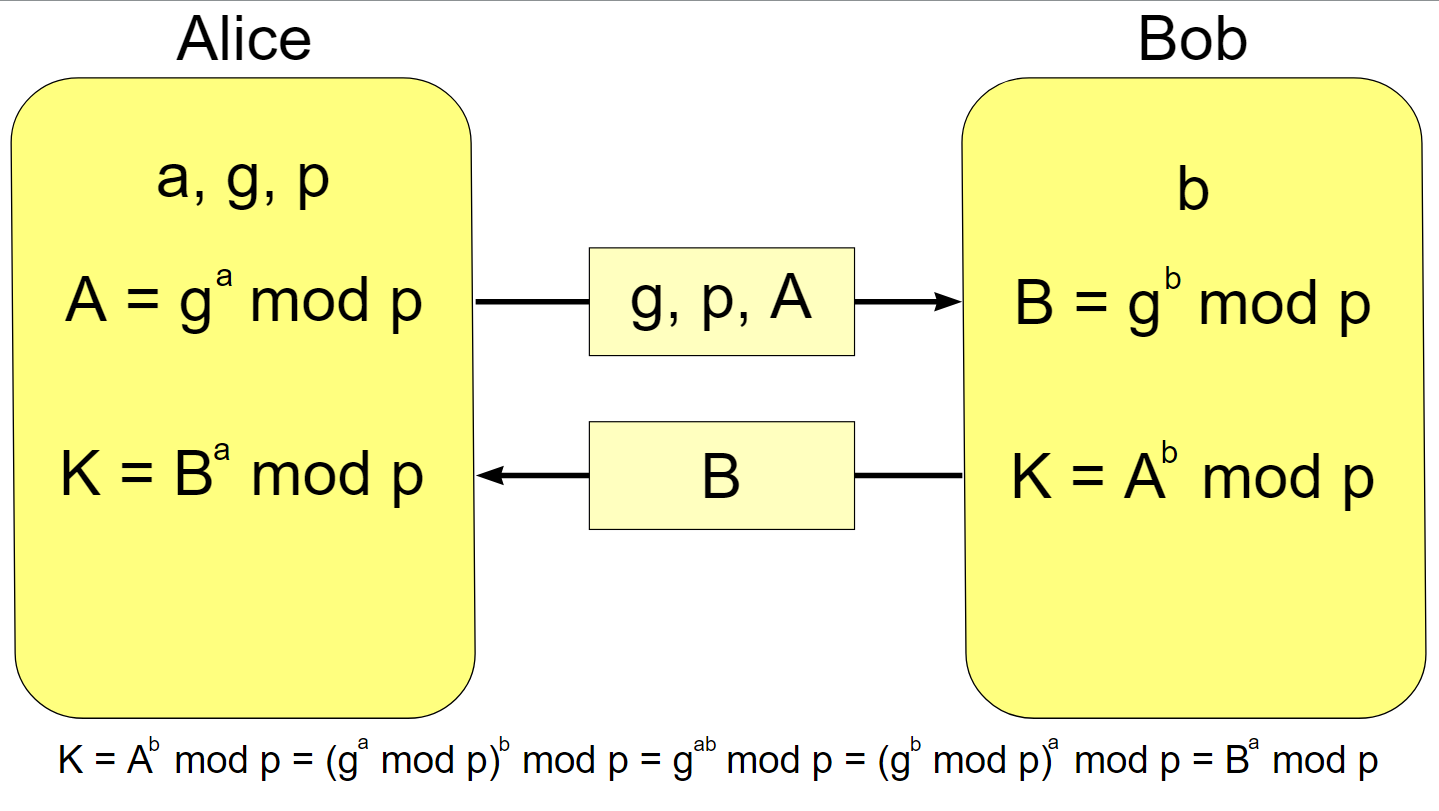
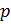 и
и 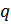 .
.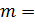
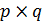 , которое называется модулем.
, которое называется модулем.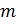 :
: 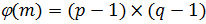 .
.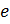 :
: 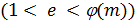 , взаимно простое со значением функции
, взаимно простое со значением функции 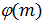 .
.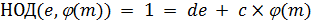 и вычислить число
и вычислить число 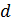 (например, при помощи расширенного алгоритма Евклида).
(например, при помощи расширенного алгоритма Евклида).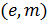
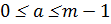
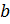 :
: 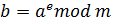
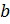
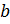 .
.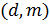 для расшифровки сообщения
для расшифровки сообщения 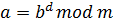 .
.