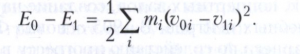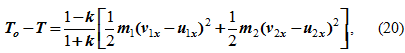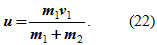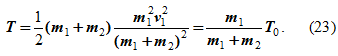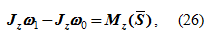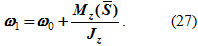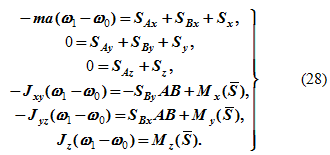18 удар двух тел потеря кинетической энергии при ударе теорема карно

Из-за
остаточных деформаций и нагревания тел
при ударе проис­ходит частичная потеря
начальной кинетической энергии
соударяющихся тел. Определим потерю
кинетической энергии при упругом ударе
тел, имеющих коэффициент восстановления
k.
Начальная кинетическая энергия тел

.

Кинетическая энергия тел в конце удара

.

Потеря кинетической энергии тел за время удара

.
(3.41)

В этом
выражении величины (v₁—u₁)
и (v₂—u₂)
представляют собой скорости, потерянные
телами при ударе. Обозначим кинетическую
энергию тел, соответствующую их
потерян­ным скоростям, Т*.
Если числовая величина

,
(3.42)

тогда выражение (3.41),
определяющее потерю кинетической
энергии тел при ударе, примет вид

Таким
образом, кинетическая энергия, потерянная
телами при упругом ударе, равна
произведению коэффициента (1-k)/(1+k)
на кинетическую энергию тел Т*,
соответствующую их потерянным ско­ростям.
При неупругом ударе, когда k=0
и и₁=и₂=и,
формула (3.41) принимает вид

.
(3.43)

Формула
(3.43) выражает теорему Карно: кинетическая
энергия, потерянная телами при неупругом
ударе, равна кинетической энергии тел,
соответствующей их потерянным скоростям.

15.5. Теорема об изменении кинетического момента

механической
системы при ударе

Теорема
об изменении кинетического момента
механической системы при ударе: изменение
кинетического момента механической
системы относительно любого неподвижного
центра при ударе равно геометрической
сумме моментов всех внешних ударных
импульсов, приложенных к точкам системы,
относительно того же центра.

.
(3.44)

Здесь

— кинетический момент системы относительно
центра О
в момент окончания действия ударных
сил;

— кинетический момент системы относительно
центра О в
момент начала действия ударных сил;


— главный
момент всех внешних ударных импульсов,
приложенных к точкам системы, относи­тельно
центра О.

Из
уравнения (3.44) при отсутствии внешних
ударных импульсов, т.е.
при

имеем

.

Таким
образом, если
к точкам
механической системы приложены только
внутренние ударные импульсы, то
кинетический момент системы относительно
любого центра не изменяется.

Векторному уравнению (3.44) соответствуют
три уравнения в проекциях на оси
координат:

т.
е. изменение
кинетического момента механической
системы относи­тельно любой оси при
ударе равно сумме моментов всех внешних
ударных импульсов, приложенных к точкам
системы относительно той же оси.

15.6. Действие ударных сил на твердое тело, вращающееся вокруг неподвижной оси и совершающее плоское движение

Вращение
тела вокруг неподвижной оси.
Предположим, что твердое тело вращается
вокруг неподвижной оси z.
В момент, когда оно имело угловую скорость
ω₀,
на него подей­ствовали внешние ударные
силы. Определим изменение угловой
скорости тела под действием этих сил.
Для этого воспользуемся уравнением

.

Кинетический
момент твердого тела относительно оси
вращения равен произведению момента
инерции тела относительно этой оси на
угловую скорость тела , т. е.

.

Подставим эти
значения в уравнение:

,

откуда

.

Таким
образом, изменение
угловой скорости твердого тела,
вращаю­щегося вокруг неподвижной
оси, под действием внешних ударных сил
равно сумме моментов импульсов этих
сил относительно той же оси.

Плоское
движение тела. Выясним
влияние внешних ударных сил на плоское
движение твердого тела. Рассмотрим это
движение тела как совокупность двух
движений: поступательного движения
вместе с центром масс и враще­ния
вокруг оси,
проходящей
через центр
масс перпендикулярно той плоскости, в
которой он
движется. В плоскости движения центра
масс проведем оси х
и у.
Предполо­жим, что в момент начала
действия ударных сил скорость центра
масс была

а угловая скорость –

Обозначим скорость центра масс в момент
конца действия ударных сил

а угловую скорость тела — ω.
Изменение проекций скорости центра
масс определяют два уравнения:

,
(3.45)

где

— проекции внешнего ударного импульса

на оси х
и у.

Так
как dL_ζr/dt
= dL_r/dt,
то изменение угловой скорости тела
определяет уравнение:

,
(3.46)

где

— момент инерции тела относительно
подвижной оси ζ,
проходя­щей через центр тяжести
перпендикулярно плоскости ху;

— момент внешнего ударного импульса

относительно той же оси.

Таким
образом, внешние
ударные силы, действующие на
твердое
тело,
совершающее
плоское
движение,
вызывают конечное изменение скорости
центра масс тела, определяемое уравнениями
(3.45), и конечное
изменение угловой скорости тела,
определяемое уравнением
(3.46).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Из рассуждений, приведенных в § 153, следует, что при неупругом ударе происходит потеря кинетической энергии соударяющихся тел. Наибольшей эта потеря будет при абсолютно неупругом ударе. Подсчитаем, какую кинетическую энергию теряет система при абсолютно неупругом ударе двух тел.

Считая, что соударяющиеся тела движутся поступательно, и обозначая их общую скорость после абсолютно неупругого удара через и, получим для кинетической энергии системы в начале и в конце удара значения:

(162)

Потерянная при ударе кинетическая энергия равна Представим эту разность в виде

Так как из формулы (160) следует, что

то отсюда

Подставляя в правую часть равенства (163) вместо их значения из формул (162), а вместо правую часть выражения (164), получим:

или

Разности показывают, насколько уменьшилась при ударе скорость каждого из соударяющихся тел. Их можно назвать потерянными при ударе скоростями. Тогда из формулы (165) вытекает следующая теорема Карно кинетическая энергия, потерянная системой тел при абсолютно неупругом ударе, равна той кинетической энергии, которую имела бы система, если бы ее тела двигались с потерянными скоростями.

Если удар не является абсолютно неупругим то аналогичными преобразованиями можно найти, что кинетическая энергия, потерянная при ударе двух тел, определяется равенством

Рассмотрим частный случай абсолютно неупругого удара по первоначально неподвижному телу. В этом случае и

Тогда

или

Формула (166) показывает, какая энершя остается у системы после удара. Отметим два интересных предельных случая.

Рис. 380

1. Масса ударяющего тела много больше массы ударяемого . В этом случае можно считать и формула (166) дает

Следовательно, хотя удар и является абсолютно нспругим, потеря кинетической энергии при ударе почти не происходит, и система после удара начнет двигаться почти с той же кинетической энергией, которая у нее была в начале удара.

На практике такой результат нужно, очевидно, получать при забивании гвоздей, свай и т. п. Следовательно, в этом случае нужно, чтобы масса молотка была намного больше массы гвоздя (рис. 380, а).

2. Масса ударяемого тела много больше массы ударяющего . В этом случае можно считать и формула (166) дает . Таким образом, здесь при ударе почти вся кинетическая энергия расходуется на деформацию соударяющихся тел, по окончании удара тела можно считать неподвижными.

Практически такой результат нужно, очевидно, получать при ковке, клепке и т. п. Следовательно, в этих случаях нужно, чтобы масса поковки вместе с наковальней (или масса заклепки вместе с поддержкой) была много больше массы молота (рис. 380, б).

КАРНО ТЕОРЕМА в теории удара, теорема о потере кинетической энергии при абсолютно неупругом ударе. Названа по имени Л. Н. М. Карно. При ударе система теряет часть кинетической энергии: до удара кинетическая энергия системы равнялась Е₀= ¹/₂∑_i m_iυ²_{0 i},    после   удара    —     Е₁ = ¹/₂∑_i m_iυ²_1i ,где m_i — масса i-й точки системы, υ_0i и υ_1i — скорости i-й точки до и после удара. Величина этой потери в точности равна кинетической энергии, которую имела бы система, если бы её точки двигались с так называемыми потерянными скоростями (υ_0i – υ_1i), то есть

Карно теорема является прямым следствием применения законов сохранения импульса и энергии для изолированной механической системы к явлению неупругого удара. В ряде случаев Карно теорема позволяет определять скорости тел после неупругого удара.

Удар двух тел, потеря кинетической энергии 488
 [c.551]

При абсолютно упругом ударе двух тел А = 1 и Tq = T, г. е. потери кинетической энергии не происходи . При абсолютно неупругом ударе к = 0 и
 [c.536]

Если использовать потерянные телами за время удара скорости v —u и V2 — U, го потерю кинетической энергии можно также получить в форме теоремы Карно для удара двух тел  [c.536]

ПОТЕРЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ПРИ УДАРЕ ДВУХ ТЕЛ.
 [c.267]

Потеря кинетической энергии при ударе двух тел. При неупругом ударе двух тел происходит потеря кинетической энергии, которая расходуется на остаточную деформацию и нагревание тел.
 [c.565]

При частично упругом ударе двух тел на первом этапе при возрастании деформации кинетическая энергия переходит в другие формы энергии. На втором этапе в процессе восстановления недеформиро-ванного состояния снова приобретается кинетическая энергия. При частично упругом ударе потеря кинетической энергии меньше чем при соответствующем неупругом ударе.
 [c.565]

Решение задач на подсчет потери кинетической энергии при ударе двух тел следует выполнять по приведенным выше формулам.
 [c.566]

После прямого центрального удара двух тел, массы которых = = 3 кг, Ш2 = 1 кг и скорости Uio = 5 м/с, U20 О, их скорости стали равными 1<1 = U2 = 3,75 м/с. Определить потери кинетической энергии. (9,38)
 [c.353]

ПОТЕРЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ПРИ ПРЯМОМ ЦЕНТРАЛЬНОМ УДАРЕ ДВУХ ТЕЛ. ТЕОРЕМА КАРНО
 [c.829]

ТЛы получили формулу для потери кинетической энергии соударяющихся тел при произвольном прямом центральном ударе двух тел.
 [c.415]

Потеря кинетической энергии при ударе двух тел. Возьмем снова разрешающие формулы общей задачи об ударе двух тел S ,
 [c.488]

При абсолютно неупругом ударе двух тел происходит потеря кинетической энергии, которая расходуется на остаточную деформацию и нагревание тел.
 [c.613]

Пусть Ti — кинетическая энергия системы в начале удара, Тг — кинетическая энергия системы в конце удара, mi и m2 — массы соударяющихся тел, Vi и V2 — скорости тел в начале удара, к — коэффициент восстановления недеформированного состояния при ударе. Тогда потеря кинетической энергии при прямом центральном упругом ударе двух поступательно движущихся тел вычисляется по формуле
 [c.613]

Из общей механики известно, что такой же формулой выражается потеря кинетической энергии при неупругом ударе твердых тел. Поэтому прежде часто говорили, что при внезапном расширении потока происходит потеря давления на удар, хотя в действительности при смешении двух потоков жидкости не происходит никакого удара. Единственная общая черта этих двух явлений состоит в том, что при обоих явлениях происходит некоторая потеря скорости.
 [c.119]

Выше было указано, что при неупругом и не вполне упругом ударе происходит потеря кинетической энергии. Вычислим эту потерю кинетической энергии сначала для случая неупругого прямого центрального удара двух твердых тел.
 [c.581]

Потеря кинетической энергии при неупругом ударе двух тел. Теорема Карно. Из рассуждений, приведенных в 161, следует, что при неупругом ударе происходит потеря кинетической энергии соударяющихся тел. Наибольшую величину эта потеря имеет при абсолютно неупругом ударе. Подсчитаем величину потерянной системой кинетической энергии при абсолютно неупругом ударе двух тел.
 [c.420]

Потеря кинетической энергии п 1И неупругом ударе двух тел
 [c.475]

По формуле (161) можно определить потерю кинетической энергии для случая неупругого п р я м о г о «Т1 е н т р а л ь н о г о удара двух твердых тел.
 [c.136]

Определить потерю кинетической энергии при прямом центральном ударе двух тел. Массы тел /П1 и /Пг, скорости до удара VI и 2, после удара щ и П2 коэффициент восстановления к.
 [c.147]

Потеря кинетической энергии при ударе двух тел. Теорема Карно……..479
 [c.13]

Динамика системы, состоящей из двух сталкивающихся масс молота в условиях так называемого жесткого удара лишь с определенной степенью приближения, может быть охарактеризована скоростными соотношениями (15.1)-(15.4). В нормальных условиях эксплуатации между сталкивающимися массами закладывают металл и развивающиеся ударные силы вызывают в нем пластическое течение. Это уже не соударение твердых упругих тел, а упругопластический удар со своими закономерностями. Однако можно полагать, что система замкнута, так как силы, действующие на металл, уравновешены реакцией связи основания (шабота), встречных подвижных частей или рамы. Следовательно, количество движения осталось без изменения, произошло только его перераспределение между столкнувшимися массами. Однако после удара общий уровень кинетической энергии в системе уменьшается вследствие необратимых потерь, обусловленных пластической деформацией (не учитывая рассеяния энергии на колебания и т. п.). Поэтому для реального удара вводят эмпирический коэффициент восстановления (отскока), устанавливающий соотношение между проекциями скоростей на линию центров до и после удара  [c.365]

Соотношение (4.7) составляет содержание теоремы Карно при неупругом ударе двух тел потеря кинетической энергии равна ки нетической энергии потерянных скоростец, умноженной на полоа жительный коэффициент (1 — к)/ + к). При к= 1 (абсолютно уп ругий удар) кинетическая энергия сохраняется, а при к = 0 (абсолютно неупругий удар) потеря кинетической энергии наибольшая и равна кинетической энергии потерянных скоростей.
 [c.226]

Из рассуждений, приведенных в 153, 9ледует, что при неупругом ударе происходит потеря кинетической энергии соударяющихся тел. Наибольшей эта потеря будет при абсолютно неупругом ударе. Подсчитаем, какую кинетическую энергию теряет система при абсолютно неупругом ударе двух тел.
 [c.403]

Задача № 168. Определить потерю кинетической энергии при прямом центральном ударе двух тел, а также их скорости после удара, если= тз = 2/сг, Vi = A uj eK, t)2 = 0, А = 0,5.
 [c.389]

При ударе двух тел происходит потеря кинетической энергии, т. е. оби1ая кинетическая энергия Т обоих тел после удара будет меньше их кинетической энергии Т в начале удара. Потерянная кингтическая
 [c.387]

Удар двух тел. Если два тела соударяются между собой, то, согласно п. 172, можно найти величину приращения или потери кинетической энергии. Пусть 5 — величина ударного импульса, который будем предполагать неизменно направленным в пространстве и отрицательным для ударяющего тела в течение всего удара (см. п. 172а). Тогда приращение кинетической энергии равно
 [c.154]

---

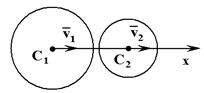
Центральным ударом тела о неподвижную преграду называют удар, при котором нормаль к поверхности преграды в точке соприкосновения проходит через центр масс тела. В противном случае удар называется нецентральным.

При рассмотрении явления удара необходимо отказаться от понятия абсолютно твердого тела.

Рассмотрим прямой центральный удар двух тел, движущихся поступательно (рисунок 2): ν₁,ν₂ – скорости тел до удара, C₁, C₂ – центры масс тел.

Рисунок 2

Внешние ударные импульсы отсутствуют, поэтому для системы двух тел количество движения системы не изменяется

m₁ν₁ + m₂ν₂ = m₁u₁ + m₂u₂. (13)

Коэффициент восстановления

k = (u₂ — u₁)/(ν₁ — ν₂). (14)

Решая совместно эти два уравнения, находим:

u₁ = ν₁ + (1+k)(v₂ — v₁)m₂ /(m₁+m₂) (15)
u₂ = ν₂ + (1+k)(v₁ — v₂)m₂ /(m₁+m₂) (16)

Если k = 0, то u₁ = u₂ = u. Отсюда скорость системы двух тел в конце неупругого удара

u = (m₁ν₁ + m₂ν₂)/(m₁+m₂) (17)

Для определения ударного импульса воспользуемся теоремой об изменении количества движения за время удара для одного из тел

m₁u₁ — m₁ν₁ = -S. (18)

Откуда:

S = (1+k)(v₁ — v₂)m₁ m₂ /(m₁+m₂) (19)

При абсолютно упругом ударе ударный импульс в два раза больше, чем при абсолютно неупругом.

Из-за остаточных деформаций и нагревания тел при ударе происходит частичная потеря начальной кинетической энергии соударяющихся тел.

При прямом центральном ударе двух тел потерю кинетической энергии можно представить в виде теоремы Карно: кинетическая энергия, потерянная при прямом центральном не вполне упругом ударе двух тел, равна (1-k)/(1+k)-той части той кинетической энергии, которую имела бы система, если бы ее тела двигались с потерянными скоростями

где m₁ и m₂ – массы соударяющихся тел, ν_1x и ν_2x – проекции скоростей соударяющихся тел на ось Ox до удара, u_1x и u_2x – проекции скоростей соударяющихся тел на ось Ox после удара.

Величины (ν_1x — u_1x) и (ν_2x — u_2x) называются потерянными скоростями и показывают, насколько уменьшилась при ударе скорость каждого из соударяющихся тел.

Если при неупругом ударе (k = 1) одно из тел (например, второе) до удара находилось в покое, то

ν₂ = 0,
T₀ = ½m₁v₁²,
T = ½(m₁ + m₂)u₁² (21)

Формула (17) принимает вид

При этом

Потеря кинетической энергии при ударе

T₀ — T = T₀ — T₀∙m₁ /(m₁+m₂), (24)

откуда

T₀ — T = T₀∙m₂/(m₁+m₂). (25)

При действии ударного импульса на твердое тело, вращающееся вокруг неподвижной оси, для определения угловой скорости используется теорема об изменении кинетического момента (7) или

где J_z – момент инерции вращающегося тела,
M_z(S) – момент ударного импульса относительно оси вращения тела,
ω₀, ω₁ – угловая скорость вращающегося тела соответственно до и после действия ударных импульсов.

Отсюда угловая скорость тела

При действии ударного импульса на вращающееся тело угловая скорость изменяется на величину, равную отношению момента этого импульса относительно оси вращения к моменту инерции тела относительно той же оси.

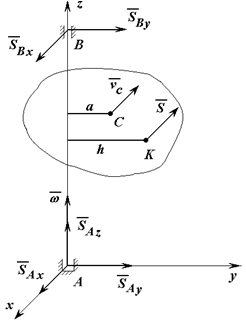
Рисунок 3

Для определения импульсов ударных реакций в подшипниках (рисунок 3) введем подвижную систему координат, проведя плоскость через центр масс, и воспользуемся теоремами об изменении количества движения (6) и об изменении кинетического момента (8). При этом:

ν_cx = -ω₀a; ν_cy = ν_cz = 0;
u_cx = -ωa;  u_cy = u_cz = 0;
L_x⁽¹⁾ = -J_zxω₀;  L_y⁽¹⁾ = -J_yzω₀;  L_z⁽¹⁾ = J_zω₀;
L_x⁽²⁾ = -J_zxω;   L_y⁽²⁾= -J_yzω;   L_z⁽²⁾ = J_zω;

здесь J_z – момент инерции тела относительно оси z, J_zx, J_yz – центробежные моменты инерции тела относительно осей z, x и осей y, z.

Получим шесть уравнений для определения импульсов ударных реакций и угловой скорости после удара:

Примеры решения задач по теме >