From Wikipedia, the free encyclopedia
In thermodynamics, Carnot’s theorem, developed in 1824 by Nicolas Léonard Sadi Carnot, also called Carnot’s rule, is a principle that specifies limits on the maximum efficiency that any heat engine can obtain.
Carnot’s theorem states that all heat engines operating between the same two thermal or heat reservoirs can’t have efficiencies greater than a reversible heat engine operating between the same reservoirs. A corollary of this theorem is that every reversible heat engine operating between a pair of heat reservoirs is equally efficient, regardless of the working substance employed or the operation details. Since a Carnot heat engine is also a reversible engine, the efficiency of all the reversible heat engines is determined as the efficiency of the Carnot heat engine that depends solely on the temperatures of its hot and cold reservoirs.
The maximum efficiency (i.e., the Carnot heat engine efficiency) of a heat engine operating between cold and hot reservoirs, denoted as 

where 




Carnot’s theorem is a consequence of the second law of thermodynamics. Historically, it was based on contemporary caloric theory, and preceded the establishment of the second law.[1]
Proof[edit]
An impossible situation: A heat engine cannot drive a less efficient (reversible) heat engine without violating the second law of thermodynamics. Quantities in this figure are the absolute values of energy transfers (heat and work).
The proof of the Carnot theorem is a proof by contradiction or reductio ad absurdum (a method to prove a statement by assuming its falsity and logically deriving a false or contradictory statement from this assumption), based on a situation like the right figure where two heat engines with different efficiencies are operating between two thermal reservoirs at different temperature. The relatively hotter reservoir is called the hot reservoir and the other reservoir is called the cold reservoir. A (not necessarily reversible) heat engine 







where 







The above expression means that heat into the hot reservoir from the engine pair (can be considered as a single engine) is greater than heat into the engine pair from the hot reservoir (i.e., the hot reservoir continuously gets energy). A reversible heat engine with a low efficiency delivers more heat (energy) to the hot reservoir for a given amount of work (energy) to this engine when it is being driven as a heat pump. All these mean that heat can transfer from cold to hot places without external work, and such a heat transfer is impossible by the second law of thermodynamics.
Let’s find the values of work 





The definition of the efficiency is 
The denominator of the second expression, 

For each engine, the absolute value of the energy entering the engine, 

In the second expression, 

Having established that the right figure values are correct, Carnot’s theorem may be proven for irreversible and the reversible heat engines as shown below.[3]
Reversible engines[edit]
To see that every reversible engine operating between reservoirs at temperatures 



- All reversible heat engines that operate between the same two thermal (heat) reservoirs have the same efficiency.
The reversible heat engine efficiency can be determined by analyzing a Carnot heat engine as one of reversible heat engine.
This conclusion is an important result because it helps establish the Clausius theorem, which implies that the change in entropy 
as the entropy change, that is made during a transition from a thermodynamic equilibrium state 

Irreversible engines[edit]
Let’s think two engines, one is 



- No irreversible heat engine is more efficient than a Carnot heat engine operating between the same two thermal reservoirs.
Definition of thermodynamic temperature[edit]
The efficiency of a heat engine is the work done by the engine divided by the heat introduced to the engine per engine cycle or
-
(1)
where 



Because all reversible heat engines operating between temperatures 

-
.
(2)
In addition, a reversible heat engine operating between temperatures 






-
.
(3)
Specializing to the case that 


Therefore, if thermodynamic temperature is defined by
then the function viewed as a function of thermodynamic temperature, is
It follows immediately that
-
.
(4)
Substituting this equation back into the above equation 
-
.
(5)
Applicability to fuel cells and batteries[edit]
Since fuel cells and batteries can generate useful power when all components of the system are at the same temperature (

A Carnot battery is a type of energy storage system that stores electricity in heat storage and converts the stored heat back to electricity through thermodynamic cycles.[9]
See also[edit]
- Chambadal–Novikov efficiency
- Heating and cooling efficiency bounds
References[edit]
- ^ John Murrell (2009). «A Very Brief History of Thermodynamics». Retrieved May 2, 2014. Archive copy at the Internet Archive PDF (142 Archived November 22, 2009, at the Wayback Machine KB)
- ^ Tipler, Paul; Mosca, G. (2008). «19.2, 19.7». Physics for Scientists and Engineers (6th ed.). Freeman. ISBN 9781429201322.
- ^ «Lecture 10: Carnot theorem» (PDF). Feb 7, 2005. Retrieved October 5, 2010.
- ^ Ohanian, Hans (1994). Principles of Physics. W.W. Norton and Co. p. 438. ISBN 039395773X.
- ^ http://faculty.wwu.edu/vawter/PhysicsNet/Topics/ThermLaw2/ThermalProcesses.html Archived 2013-12-28 at the Wayback Machine, and http://www.itp.phys.ethz.ch/education/hs10/stat/slides/Laws_TD.pdf Archived 2013-12-13 at the Wayback Machine. Both retrieved 13 December 2013.
- ^ The sign of qC > 0 for the waste heat lost by the system violates the sign convention of heat.
- ^ «Fuel Cell versus Carnot Efficiency». Retrieved Feb 20, 2011.
- ^ Jacob, Kallarackel T; Jain, Saurabh (July 2005). Fuel cell efficiency redefined : Carnot limit reassessed. Q1 — Ninth International Symposium on Solid Oxide Fuel Cells (SOFC IX). USA. Archived from the original on 2016-03-04. Retrieved 2013-04-23.
- ^ Dumont, Olivier; Frate, Guido Francesco; Pillai, Aditya; Lecompte, Steven; De paepe, Michel; Lemort, Vincent (2020). «Carnot battery technology: A state-of-the-art review». Journal of Energy Storage. 32: 101756. doi:10.1016/j.est.2020.101756. ISSN 2352-152X. S2CID 225019981.
Наиболее
часто встречающимися и, безусловно,
самопроизвольными являются процессы
передачи теплоты от горячего тела к
холодному (теплопроводность) и перехода
работы в теплоту (трение). Многовековая
житейская, техническая и научная практика
человечества показали повседневную
реальность этих процессов, а также
невозможность самопроизвольного
протекания обратных процессов. Это дает
основание утверждать, что единственным
результатом любой совокупности процессов
не может быть переход теплоты от менее
нагретого тела к более нагретому
(постулат
Клаузиуса).
Другое
общее положение утверждает следующее:
единственным результатом любой
совокупности процессов не может быть
превращение теплоты в работу или теплота
наиболее холодного тела из участвующих
в круговом процессе не может служить
источником работы (постулат
Томсона).
Оба
изложенных положения являются
формулировками второго закона
термодинамики и эквивалентны друг
другу.
Цикл
Карно является простейшим круговым
процессом, рассматривает сжатие и
расширение идеального газа, дающее
механическую работу. Существенным
является то, что теплообмен в этом цикле
совершается при двух постоянных
температурах. Путем исследования цикла
Карно с помощью второго закона
термодинамики могут быть доказаны две
важнейшие теоремы.
Коэффициент
полезного действия тепловой машины,
работающей по циклу Карно, не зависит
от природы рабочего тела машины, а лишь
от температур нагревателя и холодильника.
Коэффициент полезного действия тепловой
машины, работающей необратимо, меньше
коэффициента полезного действия машины,
работающей по обратимому циклу Карно
между теми же температурами. Полученные
результаты являются общими для любых
циклических процессов, так как любой
цикл можно заменить бесконечно большим
числом бесконечно малых циклов Карно,
ограниченных бесконечно малыми отрезками
изотерм и конечными отрезками адиабат.
Таким
образом, коэффициент полезного действия
цикла Карно больше коэффициента полезного
действия любого цикла между теми же
температурами (теорема
Карно).
Следовательно, выражение для коэффициента
полезного действия циклического
процесса, записанного в виде:
,
(4.25)
(где
и
– максимальная и минимальная температуры
теплообмена рабочего тела с источником
теплоты) является общим законом.
ЭНТРОПИЯ
Из
уравнения (4.19) для коэффициента полезного
действия цикла Карно следует, что
(4.26)
Отношение
поглощенной
системой теплоты к температуре называется
приведенной
теплотой.
Уравнение показывает, что алгебраическая
сумма приведенных теплот по обратимому
циклу Карно равна нулю.
Для
бесконечно малого обратимого цикла
Карно, очевидно:
,
(4.27)
где
— элементарная приведенная теплота.
Любой цикл может быть заменен совокупностью
бесконечно малых циклов Карно, поэтому,
суммируя выражение (4.27)для всех бесконечно
малых циклов, получаем для любого
обратимого цикла:
(4.28)
Разность
интегралов поглощенных и выделенных
приведенных теплот является алгебраической
суммой всех приведенных теплот по
обратимому циклу:
(4.29)
Для
необратимого цикла Карно, принимая во
внимание уравнение (4.25), получаем:
<0
и для любого необратимого цикла
<
0. Это – так называемоенеравенство
Клаузиуса.
Интеграл по контуру можно разбить на
два интеграла рис. 4.2:
(4.30)
Таким
образом, сумма приведенных теплот
(интеграл элементарных приведенных
теплот) при переходе системы равновесным
путем из состояния (1) в состояние (2) не
зависит от пути процесса, а только от
начального (1) и конечного (2) состояний.
|
Рис. |
Следовательно,
а |
дифференциал
функции
:
.
Выражение (4.31) являются определением
функции
,
которая являетсяэнтропией.
Энтропия
системы есть функция состояния системы:
ее изменение равно сумме приведенных
теплот, поглощенных системой в равновесном
процессе. Энтропия является однозначной,
непрерывной и конечной функцией
состояния. Энтропия измеряется в тех
же единицах, что и теплоемкость
кал/град∙моль или кал/град∙г.
Для
неравновесного процесса, исходя из
уравнения (4.30), получим:
<
0 (4.31)
Полученное
выражение не означает, что в результате
неравновесного кругового процесса
изменяется энтропия системы. Энтропия
системы как функция состояния принимает
первоначальное значение, и ее изменение
равно нулю. Сумма же приведенных теплот,
полученных системой, меньше нуля,
следовательно, окружающая среда в
результате цикла получает от системы
некоторое количество приведенной
теплоты.
Из
уравнения (4.31) получаем:
<
или
<
(4.32)
Соответствующее
неравенство может быть записано в
дифференциальной форме:
>
.
Обобщая выражения (4.31) и последнее,
получаем
.
(4.33)
В
том случае, если отсутствует теплообмен
системы с окружающей средой
,
т. е. система является адиабатной,
уравнение принимает вид:
0 или в интегральной форме
0.
Таким образом, энтропия адиабатной
системы постоянна в равновесных процессах
и возрастает в неравновесных.
Исследуя
энтропию, можно предсказать направление
процесса. Если в изолированной системе
энтропия возрастает, то процесс возможен.
Если энтропия, согласно расчету должна
убывать, то процесс невозможен. При
постоянстве энтропии процесс равновесен
и система бесконечно близка к равновесию.
В изолированной системе процессы
прекратятся, когда энтропия системы
достигнет максимального значения,
возможного для данной системы при
постоянстве некоторых ее параметров,
а именно при постоянстве внутренней
энергии
и объема
(условия изолированности системы).
МЕТОДЫ
РАСЧЕТА ЭНТРОПИИ
Уравнение
(4.31), определяющее энтропию, является
единственными исходным уравнением для
термодинамического расчета изменений
энтропии системы, который возможен
только
путем подсчета приведенных
теплот в
равновесных процессах. Заменяя
элементарную теплоту в уравнении (4.31)
ее выражениями через калорические
коэффициенты (4.10), получаем для равновесных
процессов:
и
(4.34)
Уравнения
(4.34) являются полными дифференциалами
энтропии как функции переменных
,
или
,
.
Коэффициенты этих уравнений – частные
производные энтропии по соответствующим
производным. Подставив в уравнение
(4.34) значения калорических коэффициентов
для моля идеального газа (уравнение
состояния идеального газа)и
и
полагая
и
независимыми от температуры (лишь в
небольших интервалах), получим после
интегрирования в известных пределах:
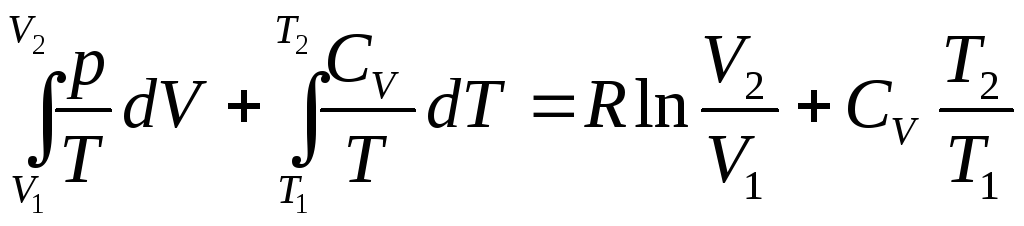
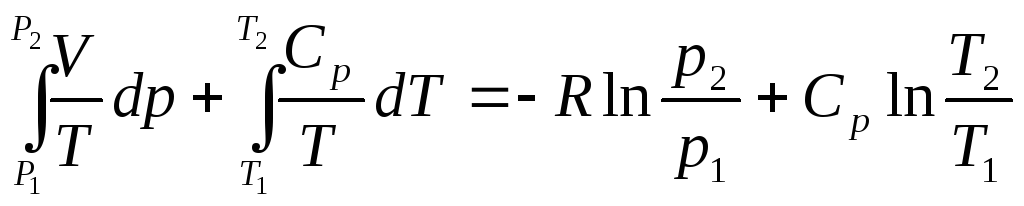
Фиксируя
величины
и
(или
и
),
а, следовательно, и
,
и объединяя постоянные члены, получим:
Обозначив
символами
и
суммы в скобках (являющиеся постоянными)
и опустив индекс2,
получим для одного моля идеального
газа:
(4.37)
Здесь
и
— константы интегрирования.
Уравнение,
используемое для идеального газа в
любом интервале температур, имеет вид:
,
(4.38)
где
(сумма
постоянной и переменной теплоемкости,
связанной с внутримолекулярным
движением). Здесь–энтропийная
константа идеального газа,
которая имеет совершенно определенную
величину для каждого газа.
Применим
полученные выше соотношения для расчетов
изменения энтропии при некоторых
процессах.
УПРАЖНЕНИЕ
4.1
Фазовые
превращения (изотермические процессы;
):
Удельная
теплота плавления бензола равна 29,92
кал/г; температура плавления
=
5,50С.
Следовательно изменение энтропии 1 г
бензола при плавлении (энтропия плавления)
равно:
кал/г∙град.
УПРАЖНЕНИЕ
4.2
Нагревание
при постоянном давлении (изобарный
процесс;
).
Из
уравнения
(4.34)
получаем:
Найдем
изменение энтропии 1 грамм-атома алюминия
при нагревании от 25 до 6000С.
Истинная атомная теплоемкость алюминия
может быть выражена уравнением:
5,006
+ 0,002564
По
уравнению (4.39) изменение энтропии будет
равно:
∙
кал/г∙град.
УПРАЖНЕНИЕ
4.3
Смешение
двух идеальных газов (изотермически-изобарный
процесс).
В
смеси идеальных газов компоненты ведут
себя независимо друг от друга. Поэтому
энтропия равновесных смесей идеальных
газов является аддитивной функцией
состава.
При
смешении двух газов в количестве
и
молей при постоянной температуре
и общем давлении
каждый газ изменяет свой объем от
первоначального до объема смеси, равного
сумме объемов газа. Изменение энтропии
при смешении является суммой изменений
энтропий каждого газа при его изотермическом
расширении. В соответствии с уравнением
(4.35) это изменение равно:
Рассчитаем
изменение энтропии, происходящее при
смешении двух молей азота и одного моля
водорода (значение температуры и
суммарного давления безразличны для
расчета).
Так
как объемы азота, водорода и смеси
находятся в отношениях
,
то изменение энтропии составит:
кал/г∙град.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Первый закон термодинамики – закон сохранения тепловых процессов, устанавливающий связь между количеством теплоты Q и изменением ∆U внутренней энергии и работой А, совершенной над внешними телами:
Q=∆U+A.
Исходя из закона, энергия не может быть создана или уничтожена: производится процесс передачи от одной системы к другой, принимая другую форму. Еще не было получено процессов, нарушающих первый закон термодинамики. Рисунок 3.12.1 показывает устройства, противоречащие первому закону.
Рисунок 3.12.1. Циклически работающие тепловые машины, запрещаемые первым законом термодинамики: 1 – вечный двигатель 1 рода, совершающий работу без потребления энергии извне; 2 – тепловая машина с коэффициентом полезного действия η>1.
Обратимый и необратимый процессы
Первый закон термодинамики не устанавливает направления тепловых процессов. Опыты показывают, что большинство тепловых процессов протекают в одном направлении. Их называют необратимыми.
Если имеется тепловой контакт двух тел с разными температурами, тогда направление теплового потока направляется от теплого к холодному. Самопроизвольной передачи тепла от тела с низкой температуры к телу с высокой не наблюдается. Отсюда следует, что теплообмен с конечной разностью температур считается необратимым.
Обратимым процессом называется переход системы из одного равновесного расстояния в другое, которые возможно проводить в обратном направлении в той же последовательности промежуточных равновесных состояний. Она вместе с окружающими телами возвращаются к исходному состоянию.
Если система находится в состоянии равновесия во время процесса, она называется квазистатической.
Когда рабочее тело тепловой машины контактирует с тепловым резервуаром, температура которого неизменна во время всего процесса, то только изотермический квазистатический процесс считается обратимым, так как протекает с бесконечно малой разницей температур рабочего резервуара. Если имеется два резервуара, причем с разными температурами, тогда обратимым путем можно провести процессы на двух изотермических участках.
Так как адиабатический процесс проводится в обоих направлениях (сжатие и расширение), наличие кругового процесса с двумя изотермами и двумя адиабатами (цикл Карно) говорит о том, что это и есть единственный обратимый круговой процесс, где рабочее тело контактируется с двумя тепловыми резервуарами. Остальные при наличии 2 тепловых резервуаров считаются необратимыми.
Превращение механической работы во внутреннюю энергию считаются необратимыми при наличии силы трения, диффузии в газах и жидкостях, а процесс перемешивания по причине начальной разности давлений и так далее. Все реальные процессы считаются необратимыми, даже если значения будут максимально приближены к обратимым. Обратимые рассматриваются как пример реальных процессов.
Первый закон термодинамики не различает их. Правило требует от термодинамического процесса определенного энергетического баланса, но не говорит о том, возможен ли он. Установка направления прохождения процесса определяется вторым законом термодинамики. Его формулировка может звучать как запрет на определенные термодинамические процессы.
Второй закон был трактован У. Кельвином в 1851.
В циклически действующей тепловой машине невозможно прохождение процесса, единственным результатом которого было бы преобразование в механическую работу всего количества теплоты, полученного от единственного теплового резервуара.
Предположительно, машина с такими процессами могла бы получить название вечного двигателя второго рода.
При земных условиях могла бы быть отбита энергия Мирового океана и полностью превратилась бы в ее работу. Масса воды Мирового океана – 1021 кг. Для его охлаждения хотя бы на 1 градус потребуется огромное количество энергии ≈1024 Дж, которое сравнимо с сжиганием 1017 кг угля. Вырабатываемая энергия на Земле за год в 104 раз меньше. Отсюда и вывод о том, что вечный двигатель второго рода мало вероятен, как и двигатель первого, потому как оба они недопустимы, исходя из первого закона термодинамики.
Второй закон термодинамики
Формулировка 2-го закона термодинамики была дана физиком Р. Клаузиусом.
Невозможно прохождение процесса, единственным результатом которого была бы передача энергии при помощи теплообмена от тела с низкой температуры к телу с более высокой.
Рисунок 3.12.2 объясняет процессы, которые запрещены вторым законом, но разрешены согласно первому. Они соответствуют трактовкам второго закона термодинамики.
Рисунок 3.12.2. Процессы, не противоречащие первому закону термодинамики, но запрещаемые вторым законом: 1 – вечный двигатель второго рода; 2 – самопроизвольный переход тепла от холодного тела к более теплому (идеальная холодильная машина).
Формулировки обоих законов считаются эквивалентными.
Когда тело без помощи внешних сил переходит при теплообмене от холодного к горячему, то возникает мысль о возможности создания вечного двигателя второго рода. Если такая машина получит количество теплоты Q1 от нагревателя и отдаст холодильнику Q2, тогда совершается работа A=Q1-Q2. Если бы Q2 самопроизвольно перешло к нагревателю, то конечный результат тепловой машины и идеальной холодильной машины выглядело бы таким образом Q1-Q2. Причем сам переход происходил бы без изменений холодильника. Отсюда вывод – комбинация тепловой машины и идеальной холодильной машины равноценна двигателю второго рода.
Прослеживается связь между вторым законом термодинамики и необратимостью реальных тепловых процессов. Энергия теплового движения молекул отлична от механической, электрической и так далее. Она способна превратиться в другой вид энергии только частично. Поэтому при наличии энергии теплового движения молекул любой процесс считается необратимым, так как полностью в обратном направлении он не осуществим.
Свойство, относящееся к необратимым процессам, говорит о том, что они проходят в термодинамически неравновесной системе, а результат получается в виде замкнутой системы, приближающейся к состоянию термодинамического равновесия.
Теоремы Карно
Имеются теоремы Карно, которые могут быть доказаны, исходя из второго закона термодинамики.
КПД тепловой машины, работающей при данных значениях температур нагревателя холодильника, не может иметь значение больше, чем КПД действия машины, работающей согласно обратимому циклу Карно с теми же значениями температур нагревателя и холодильника.
КПД действия тепловой машины, работающей по циклу Карно, не зависит от рода рабочего тела, а только от температур нагревателя и холодильника.
Отсюда следует, что КПД действия машины с циклом Карно считается максимальным.
η=1-Q2Q1≤ηmax=ηКарню=1-T2T1.
Знак равенства данной записи говорит об обратимости процесса. Если машина работает по циклу Карно, тогда:
Q2Q1=T2T1 или Q2T2=Q1T1.
Знаки Q1 и Q2 всегда отличаются независимо от направления цикла. Поэтому получаем:
Q1T1+Q2T2=0.
Рисунок 3.12.3 говорит о том, что данное соотношение обобщается и представляется в виде последовательности малых изометрических и адиабатических участков.
Рисунок 3.12.3. Произвольный обратимый цикл как последовательность малых изотермических и адиабатических участков.
Полный обход замкнутого обратимого цикла имеет вид:
∑∆QiTi=0 (обратимый цикл).
Откуда ∆Qi=∆Q1i+∆Q2i – количество теплоты, полученное рабочим телом на двух изотермических участках с температурой Ti. Чтобы данный цикл провести наоборот, нужно рабочее тело сконтактировать со многими тепловыми резервуарами с Ti.
Энтропия
Отношение QiTi получило название приведенного тепла. Формула показывает, что полное приведенное тепло на любом обратимом цикле равно нулю. Благодаря ей вводится еще одно понятие – энтропия, обозначаемая S. Ее открыл Р. Клаузиус в 1865 году.
При переходе из одного равновесного состояние в другое изменяется и ее энтропия. Разность энтропий двух состояний равняется приведенному теплу, полученному системой во время обратного перехода состояния.
∆S=S2-S1=∑(1)(2)∆QiобрT.
Если рассматривается адиабатический процесс ∆Qi=0, тогда энтропия S не изменяется.
Изменение энтропии ∆S во время перехода в другое состояние фиксируется как формула:
∆S=∫(1)(2)dQобрT.
Определение энтропии достаточно точное. Разность ∆S двух состояний системы подразумевает физический смысл. Если имеется необратимый переход, а необходимо найти энтропию, тогда нужно придумать обратимый процесс, который свяжет начальное и конечное состояние. После этого перейти к нахождению приведенного тепла, полученного системой.
Рисунок 3.12.4 Модель энтропии и фазовых переходов.
Рисунок 3.12.5 показывает необратимый процесс расширения шага с отсутствием теплообмена. Равновесными считаются начальное и конечное значение, изображаемые на диаграмме p, V. Точки a и b соответствуют состояниям и располагаются на одной изотерме. Чтобы найти ∆S, следует перейти к рассмотрению обратимого изотермического перехода из a в b. При изопроцессе газ получает определенное количество теплоты окружающих тел Q>0, тогда при необратимом расширении энтропия возрастет до ∆S>0.
Рисунок 3.12.5. Расширение газа в «пустоту». Изменение энтропии ∆S=QT=AT>0 где A=Q – работа газа при обратимом изотермическом расширении.
Еще одним примером необратимого процесса считается теплообмен при конечной разности температур. Рисунок 3.12.6 и показывает два тела, заключенные в адиабатическую оболочку, где начальные температуры обозначаются как T1 и T2<T1. Течение процесса теплообмена способствует выравниванию температур. Очевидно, что теплое тело отдает, а холодное принимает. Холодное тело превосходит по модулю приведенное тепло, отдаваемое горячим. Отсюда вывод – изменение энтропии в замкнутой системе необратимого процесса ∆S>0.
Рисунок 3.12.6. Теплообмен при конечной разности температур: a – начальное состояние; b – конечное состояние системы. Изменение энтропии ΔS>0.
Все самопроизвольно протекающие процессы в изолированных термодинамических процессах характеризуются ростом энтропии.
Обратимые процессы имеют постоянную энтропию ∆S≥0. Соотношение называют законом возрастания энтропии.
При любых процессах, протекающих в термодинамических изолированных системах, энтропия либо не меняется, либо возрастает.
Наличие энтропии говорит о самопроизвольно протекающем процессе, а ее рост – приближение всей системы к термодинамическому равновесию, где S принимает максимальное значение. Возрастание энтропии можно трактовать как формулировку второго закона термодинамики.
В 1878 году Л. Больцман дал вероятностное определение понятию энтропии, так как было предложено рассматривать ее в качестве меры статистического беспорядка замкнутой термодинамической системы. Все самопроизвольно протекающие процессы в таких системах приближают ее к равновесному состоянию, так как сопровождаются ростом энтропии, и направляют в сторону увеличения вероятности состояния.
Если состояние макроскопической системы содержит большое число частиц, то его реализация может предусматривать несколько способов.
Термодинамическая вероятность W системы – это количество способов, которыми реализуется данное состояние макроскопической системы, макросостояний, осуществляющих его.
Из определения имеем, что W≫1.
При наличии 1 моль газа в емкости существует число N способов размещения молекулы по двум половинам емкости: N=2NА, где NА — число Авогадро. Каждое из них – это микросостояние.
Одно из них соответствует случаю с молекулами, собранными в одной половине сосуда. Вероятность такого события приравнивается к нулю. Большое количество состояний соответствует такому, где молекулы распределяются равномерно по всей площади емкости.
Тогда равновесное состояние является наиболее вероятным.
Равновесное состояние считается состоянием наибольшего беспорядка в термодинамической системе с максимальной энтропией.
Исходя из трактовок Больцмана, энтропия S и термодинамическая вероятность W связаны:
S=k·ln W, где k=1,38·10-23 Дж/К является постоянная Больцмана. Отсюда следует, что определение энтропии определяется логарифмом числа микросостояний. Именно они способствуют реализации данного макросостояния. Тогда энтропия может быть рассмотрена в качестве меры вероятности состояния термодинамической системы.
Вероятностная трактовка второго закона термодинамики допускает самопроизвольное отклонение системы от состояния термодинамического равновесия. Их называют флуктуациями.
В системах с большим числом частиц отклонения от состояния равновесия имеют достаточно малую вероятность на существование.
Закон физики
Второй закон термодинамики гласит, что общая энтропия изолированной системы никогда не может уменьшаться с течением времени и является постоянной тогда и только тогда, когда все процессы обратимы. Изолированные системы спонтанно эволюционируют к термодинамическому равновесию, состоянию с максимальной энтропией.
Полная энтропия системы и ее окружения может оставаться постоянной в идеальных случаях, когда система находится в термодинамическом равновесии или претерпевает (фиктивный) обратимый процесс. Во всех происходящих процессах, включая спонтанные процессы, общая энтропия системы и ее окружения увеличивается, и процесс необратим в термодинамическом смысле. Увеличение энтропии объясняет необратимость природных процессов и асимметрию между будущим и прошлым.
Исторически вторым законом был эмпирический вывод, который был принят в качестве аксиомы термодинамическая теория. Статистическая механика, классическая или квантовая, объясняет микроскопическое происхождение закона.
Второй закон выражался по-разному. Его первая формулировка приписывается французскому ученому Сади Карно, который в 1824 году показал, что существует верхний предел эффективности преобразования тепла в работу теплового двигателя. Этот аспект второго закона часто назван в честь Карно.
Содержание
- 1 Введение
- 2 Различные положения закона
- 2.1 Принцип Карно
- 2.2 Утверждение Клаузиуса
- 2.3 Утверждения Кельвина
- 2.4 Эквивалентность утверждений Клаузиуса и Кельвина
- 2.5 Предложение Планка
- 2.6 Связь между утверждением Кельвина и утверждением Планка
- 2.7 Утверждение Планка
- 2.8 Принцип Каратеодори
- 2.9 Принцип Планка
- 2.10 Утверждение для системы, у которой есть известное выражение ее внутренней энергии как функции ее обширных переменных состояния
- 3 Следствия
- 3.1 Вечное движение второго рода
- 3.2 Теорема Карно
- 3.3 Неравенство Клаузиуса
- 3.4 Термодинамическая температура
- 3.5 Энтропия
- 3.6 Энергия, доступная полезная работа
- 3.7 Второй закон химической термодинамики
- 4 История
- 4.1 Рассказ Клаузиуса
- 5 Статистическая механика
- 6 Вывод из статистической механики
- 6.1 Вывод изменения энтропии для обратимых процессов
- 6.2 Вывод для систем, описываемых каноническим ансамблем
- 7 Живые организмы
- 8 Гравитационные системы
- 9 Неравновесные состояния
- 10 Стрелка времени
- 11 Необратимость
- 11.1 Парадокс Лошмидта
- 11.2 Теорема Пуанкаре о повторяемости
- 11.3 Демон Максвелла
- 12 Цитаты
- 13 См. Также
- 14 Ссылки
- 14.1 Источники
- 15 Дополнительная литература
- 16 Внешние ссылки
Введение

Первый закон термодинамики дает определение внутренней энергии термодинамической системы, и выражает закон сохранения энергии. Второй закон касается направления природных процессов. Он утверждает, что естественный процесс протекает только в одном смысле и не является обратимым. Например, когда доступен путь для проводимости и излучения, тепло всегда спонтанно перетекает от более горячего тела к более холодному. Такие явления учитываются с помощью энтропии. Если изолированная система первоначально поддерживается во внутреннем термодинамическом равновесии за счет внутреннего разделения непроницаемых стенок, а затем какая-то операция делает стенки более проницаемыми, то система спонтанно эволюционирует, чтобы достичь окончательного нового внутреннего термодинамического равновесия, и ее общая энтропия S увеличивается.
В фиктивном обратимом процессе бесконечно малое приращение энтропии (dS) системы определяется как результат бесконечно малой передачи тепла (δQ) в замкнутую систему (что позволяет вход или выход энергии — но не перенос вещества), деленный на общую температуру (T) системы в равновесии и окружающей среды, поставляющей тепло:
- d S = δ QT (замкнутая система, идеализированный фиктивный обратимый процесс). { Displaystyle mathrm {d} S = { frac { delta Q} {T}} , , , , , , , , , , , , , , , , , , , , , , , { text {(замкнутая система, идеализированный фиктивный обратимый процесс)}}.}
Для бесконечно малых количеств тепла используются разные обозначения (δ) и бесконечно малые количества энтропии (d), потому что энтропия является функцией состояния, в то время как тепло, как и работа, нет. Для фактически возможного бесконечно малого процесса без обмена массой с окружающей средой второй закон требует, чтобы приращение энтропии системы удовлетворяло неравенству
- d S>δ Q T s u r r (замкнутая система, фактически возможный, необратимый процесс). { displaystyle mathrm {d} S>{ frac { delta Q} {T_ {surr}}} , , , , , , , , , , , , , , , , , , , , , , , { text {(замкнутая система, реально возможный, необратимый процесс).}}}
Это связано с тем, что общий процесс для этого случая может включать в себя работу, выполняемую в системе ее окружением, что может иметь фрикционные или вязкие эффекты внутри системы, потому что может происходить химическая реакция или потому что теплопередача на самом деле происходит необратимо из-за конечной разницы между температурой системы (T) и температурой окружающей среды (T surr). Обратите внимание, что равенство по-прежнему применяется для чистого теплового потока,
- d S = δ QT (фактически возможна квазистатическая необратимая процедура сс без изменения состава). { Displaystyle mathrm {d} S = { frac { delta Q} {T}} , , , , , , , , , , , , , , , , , , , , , , , { text {(фактически возможный квазистатический необратимый процесс без изменения состава).}}}
что является основой точного определения абсолютного энтропия чистых веществ по измеренным кривым теплоемкости и изменение энтропии при фазовых переходах, т. е. калориметрическим методом. Введение набора внутренних переменных ξ { displaystyle xi}
- d S = δ QT — 1 T ∑ j Ξ j δ ξ j (замкнутая система, фактически возможный квазистатический необратимый процесс). { displaystyle mathrm {d} S = { frac { delta Q} {T}} — { frac {1} {T}} sum _ {j} , Xi _ {j} , дельта xi _ {j} , , , , , , , , , , , , , , , , , , , , , , , { text {(замкнутая система, фактически возможный квазистатический необратимый процесс).}}}
Второй член представляет работу внутренних переменных, которые могут быть возмущены внешними воздействиями, но система не может выполнять какую-либо положительную работу через внутренние переменные. Это утверждение вводит невозможность обращения эволюции термодинамической системы во времени и может рассматриваться как формулировка второго принципа термодинамики — формулировка, которая, конечно, эквивалентна формулировке принципа в терминах энтропии..
. нулевой закон термодинамики в его обычном кратком изложении позволяет распознать, что два тела в отношении теплового равновесия имеют одинаковую температуру, особенно то, что тестовое тело имеет ту же температуру, что и эталонное термометрическое тело.. Для одного тела, находящегося в тепловом равновесии с другим, существует неограниченное количество эмпирических температурных шкал, как правило, в зависимости от свойств конкретного эталонного термометрического тела. Второй закон допускает выделенную температурную шкалу, которая определяет абсолютную термодинамическую температуру, независимо от свойств любого конкретного эталонного термометрического тела.
Различные положения закона
Второй закон термодинамики может быть выражен многими определенными способами, наиболее известные классические утверждения — это утверждение Рудольфа Клаузиуса (1854 г.), утверждение лорда Кельвина (1851 г.), и утверждение в аксиоматической термодинамике Константина Каратеодори (1909). Эти утверждения формулируют закон в общих физических терминах, ссылаясь на невозможность определенных процессов. Утверждения Клаузиуса и Кельвина эквивалентны.
Принцип Карно
Историческое происхождение второго закона термодинамики лежит в принципе Карно. Он относится к циклу тепловой машины Карно, фиктивно работающей в предельном режиме экстремальной медленности, известном как квазистатический, так что тепло и работа передаются между подсистемами, которые всегда находятся в своих внутренних состояниях. термодинамического равновесия. Двигатель Карно — это идеализированное устройство, представляющее особый интерес для инженеров, которым важна эффективность тепловых двигателей. Принцип Карно был признан Карно в то время, когда теория теплоты серьезно рассматривалась, до признания первого закона термодинамики и до математического выражения концепции энтропия. Интерпретируемый в свете первого закона, он физически эквивалентен второму закону термодинамики и остается в силе сегодня. Первоначальные аргументы Карно были сделаны с точки зрения теории теплоты еще до открытия первого закона термодинамики. Вот некоторые примеры из его книги:
-
- … везде, где существует разница температур, может быть произведена движущая сила.
-
- Производство движущей силы в паровых двигателях происходит не за счет фактического потребления калорий, а к его транспортировке от теплого тела к холодному…
-
- Движущая сила тепла не зависит от агентов, используемых для его реализации; его количество определяется исключительно температурами тел, между которыми осуществляется, наконец, передача тепла.
. Говоря современным языком, принцип Карно может быть сформулирован более точно:
-
- Эффективность квазистатического или обратимого Цикл Карно зависит только от температур двух тепловых резервуаров и одинаков для любого рабочего тела. Двигатель Карно, работающий таким образом, является наиболее эффективным из возможных тепловых двигателей, использующих эти две температуры.
Заявление Клаузиуса
Немецкий ученый Рудольф Клаузиус заложил основы второго закона термодинамики. в 1850 году, исследуя связь между теплопередачей и работой. Его формулировка второго закона, опубликованная на немецком языке в 1854 году, известна как утверждение Клаузиуса:
Тепло никогда не может перейти от более холодного тела к более теплому без каких-либо других связанных с этим изменений, происходящих в то же время.
В заявлении Клаузиуса используется концепция «прохождения тепла». Как обычно в дискуссиях по термодинамике, это означает «чистую передачу энергии в виде тепла» и не относится к способствующей передаче в ту или иную сторону.
Тепло не может спонтанно течь из холодных областей в горячие без выполнения внешней работы в системе, что очевидно из обычного опыта охлаждения, например. В холодильнике тепло перетекает из холодного в горячее, но только под воздействием внешнего агента, холодильной системы.
Заявления Кельвина
Лорд Кельвин выразил второй закон в нескольких формулировках.
-
- Для самодействующей машины без посторонней помощи невозможно передать тепло от одного тела к другому при более высокой температуре.
-
- Невозможно с помощью неодушевленного материала вызвать механический эффект из любой части материи, охлаждая ее ниже температуры самого холодного из окружающих объектов.
Эквивалентность утверждений Клаузиуса и Кельвина
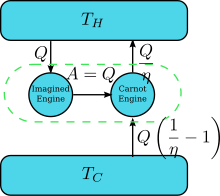
Предположим, что есть двигатель, нарушающий Кельвин. Утверждение: то есть тот, который отводит тепло и полностью преобразует его в работу циклически без какого-либо другого результата. Теперь соедините его с перевернутым двигателем Карно, как показано на рисунке. КПД нормального теплового двигателя равен η, поэтому КПД реверсивного теплового двигателя равен 1 / η. Чистый и единственный эффект объединенной пары двигателей заключается в передаче тепла Δ Q = Q (1 η — 1) { displaystyle Delta Q = Q left ({ frac {1} { eta}} -1 right)}


Предложение Планка
Планк предложил следующее предложение, выведенное непосредственно из опыта. Иногда это считают его утверждением второго закона, но он рассматривал его как отправную точку для вывода второго закона.
-
- Невозможно сконструировать двигатель, который работал бы в полном цикле и не производил бы никакого эффекта, кроме увеличения веса и охлаждения теплового резервуара.
Связь между утверждением Кельвина и предложением Планка
В учебниках почти принято говорить о «утверждении Кельвина-Планка » закона, как, например, в тексте тер Хаара и Вергеланда.
Утверждение Кельвина – Планка (или утверждение теплового двигателя) второго закона термодинамики гласит, что
-
- невозможно изобрести циклически работающее устройство, единственное действие которого состоит в том, чтобы поглощать энергию в виде тепла от единственного теплового резервуара и обеспечивать эквивалентное количество работы.
Утверждение Планка
Планк сформулировал второй закон следующим образом.
-
- Каждый процесс, происходящий в природе, происходит в том смысле, что сумма энтропий всех тел, участвующих в процессе, увеличивается. В пределе, то есть для обратимых процессов, сумма энтропий остается неизменной.
Скорее всего, как и утверждение Планка, это утверждение Уленбека и Форда для необратимых явлений.
-
- … при необратимом или спонтанном переходе от одного состояния равновесия к другому (например, при выравнивании температур двух тел A и B при контакте) энтропия всегда увеличивается.
Принцип Каратеодори
Константин Каратеодори сформулировал термодинамику на чисто математической аксиоматической основе. Его утверждение второго закона известно как принцип Каратеодори, который можно сформулировать следующим образом:
В каждой окрестности любого состояния S адиабатически замкнутой системы есть состояния, недоступные для S.
С этой формулировкой, он впервые описал концепцию адиабатической доступности и заложил основу для нового раздела классической термодинамики, часто называемого геометрической термодинамикой. Из принципа Каратеодори следует, что количество энергии, квазистатически передаваемой в виде тепла, является голономной функцией процесса, другими словами, δ Q = T d S { displaystyle delta Q = TdS}
Хотя в учебниках почти принято говорить, что принцип Каратеодори выражает второй закон, и рассматривать его как эквивалент утверждений Клаузиуса или Кельвина-Планка, это не так. Чтобы получить полное содержание второго закона, принцип Каратеодори должен быть дополнен принципом Планка, согласно которому изохорная работа всегда увеличивает внутреннюю энергию замкнутой системы, которая изначально находилась в собственном внутреннем термодинамическом равновесии.
Принцип Планка
В 1926 году Макс Планк написал важную статью по основам термодинамики. Он указал на принцип
-
- Внутренняя энергия замкнутой системы увеличивается за счет адиабатического процесса, в течение которого объем системы остается постоянным.
В этой формулировке не упоминается тепло и не упоминается температура, ни даже энтропия, и не обязательно неявно полагается на эти концепции, но подразумевает содержание второго закона. Тесно связанное с этим утверждение состоит в том, что «давление трения никогда не дает положительного результата». Планк писал: «Производство тепла трением необратимо».
Не говоря уже об энтропии, этот принцип Планка выражен в физических терминах. Это очень близко связано с утверждением Кельвина, приведенным выше. Важно, что для системы с постоянным объемом и числом молей энтропия является монотонной функцией внутренней энергии. Тем не менее, этот принцип Планка на самом деле не является предпочитаемым Планком утверждением второго закона, цитируемого выше в предыдущем подразделе настоящего раздела настоящей статьи, и основывается на концепции энтропии.
Утверждение, в некотором смысле дополняющее принцип Планка, сделано Боргнакке и Зоннтаг. Они не предлагают это как полную формулировку второго закона:
-
- … есть только один способ, которым энтропия [закрытой] системы может быть уменьшена, и это передача тепла от системы.
В отличие от только что изложенного выше принципа Планка, этот принцип явно выражается в изменении энтропии. Удаление вещества из системы также может уменьшить ее энтропию.
Утверждение для системы, у которой есть известное выражение ее внутренней энергии как функции ее обширных переменных состояния
Было показано, что второй закон эквивалентен внутренней энергии U является слабо выпуклой функцией, если записать ее как функцию экстенсивных свойств (масса, объем, энтропия,…).
Следствия
Вечное движение второго рода
До установления второго закона многие люди, заинтересованные в изобретении вечного двигателя, пытались обойти ограничения первого закона термодинамики, извлекая массивные внутренняя энергия окружающей среды как мощность машины. Такая машина называется «вечным двигателем второго рода». Второй закон декларировал невозможность создания таких машин.
Теорема Карно
Теорема Карно (1824) — это принцип, ограничивающий максимальную эффективность любого возможного двигателя. Эффективность зависит исключительно от разницы температур между горячим и холодным тепловыми резервуарами. Теорема Карно утверждает:
- Все необратимые тепловые двигатели между двумя тепловыми резервуарами менее эффективны, чем двигатель Карно, работающий между одними и теми же резервуарами.
- Все обратимые тепловые двигатели между двумя тепловыми резервуарами одинаково эффективен с двигателем Карно, работающим между одними и теми же резервуарами.
В его идеальной модели теплота калорий, преобразованная в работу, может быть восстановлена путем обращения движения цикла, концепция, впоследствии известная как термодинамическая обратимость. Карно, однако, предположил, что некоторая часть калорий теряется, а не превращается в механическую работу. Следовательно, ни одна настоящая тепловая машина не могла реализовать обратимость цикла Карно и была признана менее эффективной.
Хотя этобыло сформулировано с точки зрения калорийности (см. Устаревшую теорию калорий ), а не энтропии, это было ранним пониманием второго закона.
Неравенство Клаузиуса
теорема Клаузиуса (1854) утверждает, что в циклическом процессе
- ∮ δ QT ≤ 0. { displaystyle oint { frac { delta Q} {T}} leq 0.}
Равенство выполнено в обратимом случае и строгое неравенство выполнено в необратимом случае. Обратимый случай используется для введения функций состояния энтропия. Это связано с тем, что в циклических процессах изменения функций состояния равно нулю от функций состояния.
Термодинамическая температура
Для произвольного теплового двигателя эффективность составляет:
- η = W nq H = q H — q C q H = 1 — q C q H (1) { displaystyle eta = { frac {W_ {n}} {q_ {H}}} = { frac {q_ {H} -q_ {C}} {q_ {H}}} = 1 — { frac {q_ { C}} {q_ {H}}} qquad (1)}
где W n — это чистая работа, выполненная за цикл. Таким образом, эффективность зависит только от q C/qH.
. Теорема Карно утверждает, что все реверсивные двигатели, работающие между одними и теми же тепловыми резервуарами, одинаково эффективны. Таким образом, любой реверсивный тепловой двигатель, работающий между температурами T 1 и T 2, должен иметь одинаковый КПД, то есть есть КПД зависит только от температуры: q C q H = f (TH, TC) (2). { displaystyle { frac {q_ {C}} {q_ {H}}} = f (T_ {H}, T_ {C}) qquad (2).}
Кроме того, работает обратимая тепловая машина. между температурами T 1 и T 3 должен иметь такую же эффективность, как и цикл, состоящий из двух циклов, один между T 1 и другой (промежуточной) температурой T 2, а второй — между T 2 и T 3. Это может быть только в том случае, если
- f (T 1, T 3) = q 3 q 1 = q 2 q 3 q 1 q 2 = f (T 1, T 2) f (T 2, T 3). { displaystyle f (T_ {1}, T_ {3}) = { frac {q_ {3}} {q_ {1}}} = { frac {q_ {2} q_ {3}} {q_ {1 } q_ {2}}} = f (T_ {1}, T_ {2}) f (T_ {2}, T_ {3}).}
Теперь рассмотрим случай, когда T 1 { displaystyle T_ {1}}
- f (T 2, T 3) = f (T 1, T 3) f (T 1, T 2) = 273,16 ⋅ f (T 1, Т 3) 273,16 ф (Т 1, Т 2). { displaystyle f (T_ {2}, T_ {3}) = { frac {f (T_ {1}, T_ {3})} {f (T_ {1}, T_ {2})}} = { frac {273.16 cdot f (T_ {1}, T_ {3})} {273.16 cdot f (T_ {1}, T_ {2})}}.}
Следовательно, если термодинамическая температура определяется
- T = 273,16 ⋅ f (T 1, T) { displaystyle T = 273.16 cdot f (T_ {1}, T) ,}
тогда функция f, рассматриваемая как функция термодинамической температуры, просто
- е (Т 2, Т 3) = Т 3 Т 2, { displaystyle f (T_ {2}, T_ {3}) = { frac {T_ {3}} {T_ {2}}},}
и эталонная температура T 1 будет иметь значение 273,16. (Можно использовать любую эталонную температуру и любое положительное числовое значение — выбор здесь соответствует шкале Кельвина.)
Энтропия
Согласно равенству Клаузиуса, для обратного процесса
- ∮ δ QT = 0 { displaystyle oint { frac { delta Q} {T}} = 0}
Это означает линейный интеграл ∫ L δ QT { displaystyle int _ { L} { frac { delta Q} {T}}}
Итак, мы можем определить функцию состояния S, называемую энтропией, которая для обратного процесса или для теплопередачи удовлетворяет
- d S = δ QT { displaystyle dS = { frac { delta Q} {T }} !}
Таким образом мы можем получить разность энтропии, только интегрировав приведенную выше формулу. Чтобы получить абсолютное значение, нам нужен третий закон термодинамики, который гласит, что S = 0 при абсолютном нуле для идеальных кристаллов.
для любого необратимого процесса, поскольку энтропия является функцией состояния, мы всегда можем связать начальное и конечное состояния с воображаемым производственным процессом и интегрировать по этому пути, чтобы вычислить разницу в энтропии.
Теперь измените обратимый процесс и объедините его с упомянутым необратимым процессом. Применяя неравенство Клаузиуса к этому циклу,
- — Δ S + ∫ δ QT = ∮ δ QT < 0 {displaystyle -Delta S+int {frac {delta Q}{T}}=oint {frac {delta Q}{T}}<0}
Таким образом,
- Δ S ≥ ∫ δ QT { displaystyle Delta S geq int { frac { delta Q} {T}} , !}
где равенство выполнено, если преобразование обратимо.
Обратите внимание, что если процесс является адиабатическим процессом, то δ Q = 0 { displaystyle delta Q = 0}

Энергия, доступная полезная работа
Важным и показательным идеализированным частным случаем является рассмотрение применения Второго закона к сценарию изолированной (называемой целостной системой или вселенной), состоящий из двух частей: представляющая интерес подсистемы и окружения подсистемы. Эти окружения кажутся настолько большими, что их можно рассматривать как неограниченный резервуар тепла при температуре T R и давлении P R — так что независимо от того, сколько тепла передается (или из) подсистемы, температура окружающей среды останется T R ; и независимо от того, насколько объем подсистемы расширяется (или сжимается), давление окружающей среды будет оставаться P R.
Какие бы изменения в dS и dS R ни происходили в энтропиях подсистемы системы, и окружающей среды индивидуально, согласно Второму закону энтропия S tot изолированной полной системы не должна уменьшаться:
- d S tot = d S + d SR ≥ 0 { displaystyle dS _ { mathrm {tot}} = dS + dS_ {R } geq 0}
Согласно первому закону термодинамики, изменение dU внутренней энергии подсистемы является суммой тепло δq, добавленное к подсистеме, за вычетом любой работы δw, выполненной подсистемой, плюс любая чистая химическая энергия, поступающая в подсистему d ∑μ iRNi, так что:
- d U = δ q — δ вес + d (∑ μ я RN я) { displaystyle dU = delta q- delta w + d ( sum mu _ {iR} N_ {i}) ,}
где μ iR — это химический потенциал химических во внешней среде.
Теперь тепло, покидающий резервуар и поступающее в подсистему, равно
- δ q = TR (- d SR) ≤ TR d S { displaystyle delta q = T_ {R} (- dS_ {R}) leq T_ {R} dS}
где мы впервые использовали определение энтропии в классической термодинамике (альтернативно, в статистической термодинамике можно вывести связь между изменением энтропии, температурой и поглощенным теплом); а затем неравенство Второго закона сверху.
Из этого следует, что любая сетевая работа δw, выполняемая подсистема, должна подчиняться
- δ w ≤ — d U + TR d S + ∑ μ i R d N i { displaystyle delta w leq -dU + T_ {R} dS + sum mu _ {iR} dN_ {i} ,}
Полезно разделить работу δw, выполняемую подсистемой, на полезную работу δw u, что может быть выполнено подсистемой сверх работы p R dV, выполняемой просто путем расширения подсистемы против окружающего внешнего давления, что дает следующее соотношение для полезной работы (эксергия), что можно сделать:
- δ wu ≤ — d (U — TRS + п RV — ∑ μ я RN я) { Displaystyle delta w_ {u} leq -d (U-T_ {R} S + p_ {R} V- sum mu _ {iR} N_ {i}) ,}
Правую часть удобно определить как точную производную термодинамическую систему, называемую доступностью или эксергия E = U — TRS + p RV — ∑ μ i RN i { displaystyle E = U-T_ {R} S + p_ {R} V- sum mu _ {iR} N_ {i}}
Следовательно, Второй закон подразумевает, чт о для любого процесса, может рассматриваться как просто разделен на подсистему и неограниченный резервуар температуры и давления, с которым он контактирует,
- d E + δ wu ≤ 0 { displaystyle dE + delta w_ {u} leq 0 ,}
т.е. изменение эксергии подсистемы плюс полезная работа, выполняемая подсистема (или изменение эксергии подсистемы за вычетом какой-либо работы, которая выполняется резервуаром давления, выполненной в системе), должно быть меньше или равно нулю.
В итоге, если в качестве окружения системы в реальном мире выбрано надлежащее эталонное состояние, подобное бесконечному резервуару, то второй закон предсказывает уменьшение E для необратимого процесса и отсутствие изменений для обратимого процесса..
- d S tot ≥ 0 { displaystyle dS_ {tot} geq 0}
эквивалентно d E + δ wu ≤ 0 { displaystyle dE + delta w_ {u} leq 0 }
Это выражение вместе со эталонным состоянием позволяет инженеру-проектировщику , работающему в макроскопическом масштабе (выше термодинамического предела ), использовать Второй закон без непосредственного измерения или рассмотрение энтропии в полностью изолированной системе. (Также см. инженер-технолог ). Эти рассматриваемые системы могут достичь равновесия с эталонным состоянием без изменения эталонного состояния. Также может быть обнаружена эффективность процесса или набора процессов, которая сравнивает его с обратимым идеалом (см. эффективность второго закона.)
Этот подход используется второму закону широко в инженерная практика, экологический учет, системная экология и другие дисциплины.
Второй закон химической термодинамики
Для спонтанного химического процесса в замкнутой системе при постоянной и постоянной нагрузке без работы, не использует фотоэлектрическую систему, неравенство Клаузиуса ΔS>Q / T surr преобразуется в условие изменения свободной энергии Гиббса
- Δ G < 0 {displaystyle Delta G<0}
или dG < 0. For a similar process at constant temperature and volume, the change in свободной энергии Гельмгольца должно быть отрицательным, Δ А < 0 {displaystyle Delta A<0}
История

Первая Теория преобразования тепла в механическую работу принадлежит Николя Леонар Сади Карно в 1824 году. Он был первым, кто правильно понял, что эффективность этого преобразования зависит от разницы температур двигателя и окружающей среды..
Признавая важная работа Джеймса Прескотта Джоуля по сохранению энергии, Рудольф Клаузиус был первым, кто сформулировал второй закон в 1850 году в такой форме: тепло не переходит самопроизвольно от холодных тел к горячим. Хотя сейчас общеизвестно, это противоречило теории теплоты, популярной в то время, которая рассматривала тепло как жидкость. Отсюда он смог вывести принцип Сади Карно и определение энтропии (1865 г.).
Основанное в 19 веке утверждение Кельвина-Планка о втором законе гласит: «Ни одно устройство, работающее в цикле, не может получать тепло из одного резервуара и произвести чистый объем работы «. Было показано, что это эквивалентно утверждению Клаузиуса.
эргодическая гипотеза также важна для подхода Больцмана. говорит, что в течение длительных периодов времени время, проведенное в некоторой области фазового пространства микросостояний с одинаковой энергией, пропорционально объему этой области, т.е. что все доступные микросостояния равновероятны в течение длительного периода времени., в нем говорится, что среднее по времени и среднее по статистическому ансамблю одинаковы.
Существует традиционная доктрина, начиная с Клаузиуса, что энтропию можно понять с точки зрения молекулярного «беспорядка» в макроскопическом система. Эта доктрина устарела.
Отчет Клаузиуса

В 1856 году немецкий физик Рудольф Клаузиус сформулировал то, что он назвал «второй фундаментальной теоремой в механической теории тепла », в следующей форме:
- ∫ δ QT = — N { displaystyle int { frac { delta Q} {T}} = — N}
где Q — тепло, T — температура, а N — «значение эквивалентности» всех некомпенсированных преобразований, участвующих в циклический процесс. Позже, в 1865 году, Клаузиус определил «эквивалентность-ценность» как энтропию. Вслед за этим определением в том же году самая известная версия второго закона была прочитана на презентации в Цюрихском философском обществе 24 апреля, в которой в конце своей презентации Клаузиус заключает:
Энтропия вселенной стремится к максимуму.
Это утверждение — самая известная формулировка второго закона. Из-за расплывчатости его языка, например вселенная, а также отсутствие определенных условий, например открытый, закрытый или изолированный, многие люди принимают это простое утверждение за то, что второй закон термодинамики применим практически ко всем вообразимым предметам. Это неправда; это утверждение — только упрощенная версия более расширенного и точного описания.
С точки зрения изменения времени математическая формулировка второго закона для изолированной системы, подвергающейся произвольному преобразованию:
- d S dt ≥ 0 { displaystyle { frac { dS} {dt}} geq 0}
где
- S — энтропия системы, а
- t — время.
Знак равенства применяется после уравновешивания. Альтернативный способ формулировки второго закона для изолированных систем:
- d S dt = S ˙ i { displaystyle { frac {dS} {dt}} = { dot {S}} _ {i}}
с S ˙ я ≥ 0 { displaystyle { dot {S}} _ {i} geq 0}
с S ˙ i { displaystyle { dot { S}} _ {i}}


Выражение второго закона для закрытых систем (т.е. допускающих теплообмен и подвижные границы, но не обмен вещества):
- d S dt знак равно Q ˙ T + S ˙ я { displaystyle { frac {dS} {dt}} = { frac { dot {Q}} {T}} + { dot {S}} _ {i} }
с S ˙ я ≥ 0 { displaystyle { dot {S}} _ {i} geq 0}
Здесь
- Q ˙ { displaystyle { dot { Q}}}
— тепловой поток в систему.
- T { displaystyle T}
— температура в точке, где тепло входит в систему.
Равенство знак имеет место в том случае, если внутри системы происходят только обратимые процессы. Если имеют место необратимые процессы (что имеет место в реальных действующих системах), знак>сохраняется. Если тепло поступает в систему в нескольких местах, мы должны вычислить алгебраическую сумму соответствующих членов.
Для открытых систем (также допускающих обмен веществами):
- d S dt = Q ˙ T + S ˙ + S ˙ i { displaystyle { frac {dS} {dt}} = { frac { dot {Q}} {T}} + { dot {S}} + { dot {S}} _ {i}}
с S ˙ i ≥ 0 { displaystyle { dot {S}} _ {i} geq 0}
Здесь S ˙ { displaystyle { dot {S}}}
Статистическая механика
Статистическая механика объясняет второй, постулируя, что материал из атомов и молекул, находящихся в постоянном движении. Конкретный набор положений и скоростей для каждой частицы в системе называется микросостоянием системы, и из-за постоянного движения система постоянно меняет свое микросостояние. Статистическая механика постулирует, что в состоянии равновесия находится система, которая может находиться, имеет одинаковую вероятность, и когда это предположение делается, оно непосредственно приводит к выводу, что второй закон должен в статистическом смысле. То есть второй закон будет в среднем со статистической вариацией порядка 1 / √N, где N — количество частиц в системе. Для повседневных (макроскопических) вероятность второго нарушения практически равна нулю. Однако для систем с небольшим количеством частиц термодинамические параметры, включая энтропию, могут показывать статистические отклонения от предсказываемых вторым законом. Классическая термодинамическая теория не выполняет этих статистическими вариациями.
Вывод из статистической механики
Первый механический аргумент кинетической теории газов о том, что столкновения молекул влекут за собой выравнивание температур и, следовательно, тенденция к равновесию объясняется Джеймс Клерк Максвелл в 1860 г.; Людвиг Больцман со своей H-теоремой 1872 г. также утвержден, что из-за столкновения газы со временем должны стремиться к Максвеллу– Распределение Больцмана.
Из-за парадокса Лошмидта, при выводе Второго закона необходимо сделать предположение относительно прошлого, а именно, что система некоррелирована когда-то в прошлом; это позволяет проводить простую вероятностную обработку. Это предположение обычно рассматривается как граничное условие, таким образом, второе в конечном итоге является следствием начальных условий где-то в прошлом, вероятно, в начале среды (Большой взрыв ), хотя предлагались и другие сценарии.
Эти допущения, в статистической механике Второй закон не является следствием фундаментального постулат, также известный как постулатной равной априорной вероятности, при условии, что ясно, что простые аргументы вероятности применяются только к будущему, в то время как для прошлого существуют вспомогательные источники информации, которые говорят нам, что это была низкая энтропия. Первая часть второго закона, которая гласит, является энтропией термически изолированной системы может увеличиваться, является тривиальным следствием постулата равной априорной вероятности, если мы ограничим понятие энтропии системы, находящимися в тепловом равновесии. Энтропия изолированной системы в тепловом равновесии, имеющее количество энергии E { displaystyle E}
- S = k B ln [Ω (E)] { displaystyle S = К _ { mathrm {B}} ln left [ Omega left (E right) right] ,}
где Ω (E) { displaystyle Omega left (E right) }





Предположим, у нас есть изолированная система, макроскопическое состояние задается рядом. Эти макроскопические переменные могут, например, относиться к общему объему, положению поршней в системе и т.д. Тогда Ω { displaystyle Omega}

Если переменная изначально была зафиксирована на каком-то значении, то после выпуска и когда будет достигнуто новое равновесие, переменная саморегулируется так, чтобы Ω { displaystyle Omega}


Вывод изменения энтропии для обратимых процессов
Вторая часть Второго закона гласит, что изменение энтропии системы, претерпевающей обратимый процесс, определяется выражением:
- d S = δ QT { displaystyle dS = { frac { delta Q} {T}}}
где температура определяется как:
- 1 k BT ≡ β ≡ d ln [Ω (E)] d E { Displaystyle { гидроразрыва {1} {к _ { mathrm {B}} T}} эквив бета экв { гидроразрыва {d ln left [ Omega left (E right) right]} { dE}}}
См. здесь для обоснования этого определения. Предположим, что в системе есть некоторый внешний параметр x, который можно изменить. В общем, собственные энергетические состояния системы будут зависеть от x. Согласно адиабатической теореме квантовой механики, в пределе бесконечно медленного изменения гамильтониана системы система останется в том же собственном энергетическом состоянии и, таким образом, изменит свою энергию в соответствии с изменением энергии собственное состояние энергии, в котором оно находится.
Обобщенная сила X, соответствующая внешней переменной x, определяется таким образом, что X dx { displaystyle Xdx}

- X = — d E rdx { displaystyle X = — { frac {dE_ {r}} {dx}}}
Поскольку система может находиться в любом собственном энергетическом состоянии в интервале δ E { displaystyle delta E}
- X = — ⟨d E rdx⟩ { displaystyle X = — left langle { frac {dE_ {r}} {dx}} right rangle ,}
Чтобы оценить среднее значение, мы разделяем Ω (E) { displaystyle Omega left (E right)}




- Ω (E) = ∑ Y Ω Y (E) { displaystyle Omega left (E right) = sum _ {Y} Omega _ {Y} left (E right) ,}
Среднее значение, определяющее обобщенную силу, теперь может быть написано:
- X = — 1 Ω (E) ∑ YY Ω Y (E) { displaystyle X = — { frac {1} { Omega left (E right)}} sum _ {Y} Y Omega _ {Y} left (E right) ,}
Мы можем связать это с производной энтропии по x при постоянной энергии E следующим образом. Предположим, мы заменим x на x + dx. Тогда Ω (E) { displaystyle Omega left (E right)}





- NY (E) = Ω Y (E) δ EY dx { displaystyle N_ {Y} left (E right) = { frac { Omega _ {Y} left (E right)} { delta E}} Ydx ,}
такие собственные состояния энергии. Если Y dx ≤ δ E { displaystyle Ydx leq delta E}






- NY (E) — NY (E + δ E) { displaystyle N_ {Y} left (E right) -N_ {Y} left (E + delta E right) ,}
, таким образом, является чистым вкладом в увеличение Ω { displaystyle Omega}




Выражение вышеприведенного выражения как производную по E и суммирование по Y дает выражение:
- (∂ Ω ∂ x) E = — ∑ YY (∂ Ω Y ∂ E) x = (∂ (Ω Икс) ∂ E) Икс { Displaystyle влево ({ frac { partial Omega} { partial x}} right) _ {E} = — sum _ {Y} Y left ({ frac { partial Omega _ {Y}} { partial E}} right) _ {x} = left ({ frac { partial left ( Omega X right)} { partial E}} right) _ {x} ,}
Таким образом, логарифмическая производная от Ω { displaystyle Omega}
- (∂ ln ( Ω) ∂ Икс) Е знак равно β Икс + (∂ Икс ∂ E) Икс { Displaystyle влево ({ гидроразрыва { partial ln left ( Omega right)} { partial x}} right) _ {E} = beta X + left ({ frac { partial X} { partial E}} right) _ {x} ,}
Первый член является интенсивным, т. Е. Не масштабируется вместе с системой размер. Напротив, последний член масштабируется как обратный размер системы и, таким образом, обращается в нуль в термодинамическом пределе. Таким образом, мы обнаружили, что:
- (∂ S ∂ x) E = XT { displaystyle left ({ frac { partial S} { partial x}} right) _ {E} = { frac { X} {T}} ,}
Объединяя это с
- (∂ S ∂ E) x = 1 T { displaystyle left ({ frac { partial S} { partial E}} right) _ {x} = { frac {1} {T}} ,}
Дает:
- d S = (∂ S ∂ E) xd E + (∂ S ∂ x) E dx = d ET + XT dx = δ QT { displaystyle dS = left ({ frac { partial S} { partial E}} right) _ {x} dE + left ({ frac { partial S} { partial x}} right) _ {E} dx = { frac {dE} {T}} + { frac {X} {T}} dx = { frac { delta Q} {T}} ,}
Вывод для систем, описываемых каноническим ансамблем
Если система находится в тепловом контакте с термостатом при некоторой температуре T, то в равновесии распределение вероятностей по собственным значениям энергии определяется выражением канонический ансамбль :
- P j = exp (- E jk BT) Z { displaystyle P_ {j} = { frac { exp left (- { frac {E_ {j}} {k _ { mathrm) {B}} T}} right)} {Z}}}
Здесь Z — коэффициент, нормализующий сумму всех вероятностей к 1, эта функция известна как функция распределения . Теперь рассмотрим бесконечно малое обратимое изменение температуры и внешних параметров, от которых зависят уровни энергии. Это следует из общей формулы для энтропии:
- S = — k B ∑ j P j ln (P j) { displaystyle S = -k _ { mathrm {B}} sum _ {j} P_ { j} ln left (P_ {j} right)}
, что
- d S = — k B ∑ j ln (P j) d P j { displaystyle dS = -k _ { mathrm { B}} sum _ {j} ln left (P_ {j} right) dP_ {j}}
Вставка формулы для P j { displaystyle P_ {j}}
- d S = 1 T ∑ j E jd P j = 1 T ∑ jd (E j P j) — 1 T ∑ j P jd E j = d E + δ WT = δ QT { displaystyle dS = { frac {1} {T}} sum _ {j} E_ {j} dP_ {j} = { frac {1} {T}} sum _ {j} d left (E_ {j} P_ {j} right) — { frac {1} {T}} sum _ {j} P_ {j} dE_ {j} = { frac {dE + delta W} { T}} = { frac { delta Q} {T}}}
Живые организмы
Есть два основных способа формулирования термодинамики: (а) через переходы от одного состояния термодинамического равновесия к другому, и (б) посредством циклических процессов, с помощью которых система остается неизменной, в то время как общая энтропия окружающей среды увеличивается. Эти два способа помогают понять процессы жизни. Термодинамика живых организмов рассматривалась многими авторами, такими как Эрвин Шрёдингер, Леон Бриллюэн и Исаак Азимов.
В справедливом приближении живые организмы можно рассматривать как примеры (б). Приблизительно физическое состояние животного меняется день ото дня, оставляя животное почти неизменным. Животные потребляют пищу, воду и кислород и в результате метаболизма выделяют продукты распада и тепло. Растения получают лучистую энергию от солнца, которую можно рассматривать как тепло, а также углекислый газ и воду. Они выделяют кислород. Таким образом они растут. В конце концов они умирают, а их останки гниют, превращаясь в основном обратно в углекислый газ и воду. Это можно рассматривать как циклический процесс. В целом, солнечный свет исходит от источника с высокой температурой, солнца, и его энергия передается в поглотитель с более низкой температурой, то есть излучается в космос. Это увеличение энтропии окружающей среды растения. Таким образом, животные и растения подчиняются второму закону термодинамики, рассматриваемому с точки зрения циклических процессов.
Живые организмы можно рассматривать как открытые системы, потому что материя входит в них и выходит из них. Термодинамика открытых систем в настоящее время часто рассматривается с точки зрения переходов от одного состояния термодинамического равновесия к другому или с точки зрения потоков в приближении локального термодинамического равновесия. Проблема для живых организмов может быть дополнительно упрощена путем приближения, предполагающего установившееся состояние с неизменными потоками. Общие принципы производства энтропии для таких приближений являются предметом нерешенных текущих споров или исследований.
Гравитационные системы
Обычно системы, для которых гравитация не важна, имеют положительную теплоемкость, что означает, что их температура повышается вместе с их внутренней энергией. Следовательно, когда энергия течет от высокотемпературного объекта к низкотемпературному объекту, температура источника уменьшается, а температура стока увеличивается; следовательно, разница температур со временем уменьшается.
Это не всегда так для систем, в которых важна гравитационная сила: системы, которые связаны своей собственной гравитацией, такие как звезды, могут иметь отрицательную теплоемкость. По мере того как они сжимаются, их общая энергия и энтропия уменьшаются, но их внутренняя температура может повышаться. Это может быть значительным для протозвезд и даже для планет газовых гигантов, таких как Юпитер.
. Поскольку гравитация является самой важной силой, действующей в космологических масштабах, может быть трудно или невозможно применить второй закон к Вселенная в целом.
Неравновесные состояния
Теория классической или равновесной термодинамики идеализирована. Главный постулат или предположение, часто даже не сформулированное явно, — это существование систем в их собственных внутренних состояниях термодинамического равновесия. В общем, область пространства, содержащая физическую систему в данный момент времени, которая может быть обнаружена в природе, не находится в термодинамическом равновесии, если читать в самых строгих терминах. Говоря проще, ничто во всей Вселенной не находится или никогда не находилось в истинном термодинамическом равновесии.
Для целей физического анализа часто бывает достаточно удобно сделать предположение о термодинамическом равновесии. Такое предположение может быть обосновано методом проб и ошибок. Если предположение обосновано, оно часто может быть очень ценным и полезным, поскольку делает доступным теорию термодинамики. Элементы предположения о равновесии состоят в том, что система остается неизменной в течение неопределенно долгого времени и что в системе так много частиц, что ее дисперсную природу можно полностью игнорировать. При таком предположении о равновесии, как правило, нет никаких макроскопически обнаруживаемых флуктуаций. Существует исключение, случай критических состояний, которые демонстрируют невооруженным глазом явление критической опалесценции. Для лабораторных исследований критических состояний требуется исключительно длительное время наблюдения.
Во всех случаях допущение термодинамического равновесия, сделанное однажды, подразумевает, как следствие, то, что никакая предполагаемая «флуктуация» не изменяет энтропию системы.
Легко может случиться так, что физическая система демонстрирует внутренние макроскопические изменения, достаточно быстрые, чтобы опровергнуть предположение о постоянстве энтропии. Или что в физической системе так мало частиц, что природа частиц проявляется в наблюдаемых флуктуациях. Тогда следует отказаться от предположения о термодинамическом равновесии. Не существует безоговорочного общего определения энтропии для неравновесных состояний.
Есть промежуточные случаи, в которых предположение о локальном термодинамическом равновесии является очень хорошим приближением, но, строго говоря, все же приближение, не теоретически идеальное.
Для неравновесных ситуаций в целом может быть полезно рассмотреть статистические механические определения других величин, которые можно удобно назвать «энтропией», но их не следует путать или смешивать с термодинамической энтропией, правильно определенной для второй закон. Эти другие величины действительно принадлежат статистической механике, а не термодинамике, первичной области второго закона.
Физика макроскопически наблюдаемых флуктуаций выходит за рамки данной статьи.
Стрела времени
Второй закон термодинамики — это физический закон, не симметричный изменению направления времени на противоположное. Это не противоречит симметриям, наблюдаемым в фундаментальных законах физики (в частности, CPT-симметрия ), поскольку второй закон статистически применяется к асимметричным по времени граничным условиям. Второй закон связан с разницей между движением вперед и назад во времени или с принципом, согласно которому причина предшествует следствию (причинная стрела времени, или причинность ).
Необратимость
Необратимость термодинамических процессов является следствием асимметричного характера термодинамических операций, а не каких-либо внутренне необратимых микроскопических свойств тел. Термодинамические операции — это макроскопические внешние воздействия на участвующие тела, а не производные от их внутренних свойств. Существуют известные «парадоксы», которые возникают из-за неспособности признать это.
Парадокс Лошмидта
Парадокс Лошмидта, также известный как парадокс обратимости, является возражением, что он не должен можно вывести необратимый процесс из симметричной во времени динамики, описывающей микроскопическую эволюцию макроскопической системы.
По мнению Шредингера, «теперь совершенно очевидно Не важно, каким образом вы должны переформулировать закон энтропии — или, если уж на то пошло, все другие необратимые утверждения — чтобы их можно было вывести из обратимых моделей. Вы не должны говорить об одной изолированной системе, а, по крайней мере, о двух, которые вы можете на данный момент считать изолированными от остального мира, но не всегда друг от друга ». Эти две системы изолированы друг от друга стеной, пока она устраняется термодинамической операцией, как это предусмотрено законом. Термодинамическая операция накладывается извне, не подчиняется обратимым микроскопическим динамическим законам, которые управляют составными частями систем. Это причина необратимости. Формулировка закона в данной статье соответствует совету Шредингера. Причинно-следственная связь логически предшествует второму закону, а не выводится из него.
Теорема Пуанкаре о возвращении
Теорема Пуанкаре о возвращении рассматривает теоретическое микроскопическое описание изолированной физической системы. Его можно рассматривать как модель термодинамической системы после того, как термодинамическая операция удалила внутреннюю стенку. Система будет после достаточно длительного время вернуться в микроскопически определяемое состояние, очень близкое к исходному. Время повторения Пуанкаре — это промежуток времени, прошедший до возвращения. Это чрезвычайно долго, вероятно, дольше, чем время жизни Вселенной, и сильно зависит от геометрии стены, которая была удалена в результате термодинамической операции. Теорема о возвращении может восприниматься как явно противоречащая второму закону термодинамики. Однако более очевидно, что это просто микроскопическая модель термодинамического равновесия в изолированной системе, образованной удалением стены между двумя системами. Для типичной термодинамической системы время повторения настолько велико (во много раз больше, чем время жизни Вселенной), что практически невозможно наблюдать повторение. Тем не менее можно было бы вообразить, что можно дождаться повторения Пуанкаре, а затем снова вставить стенку, которая была удалена термодинамической операцией. Тогда очевидно, что появление необратимости происходит из-за полной непредсказуемости повторения Пуанкаре, учитывая только то, что начальное состояние было одним из термодинамических равновесий, как это имеет место в макроскопической термодинамике. Даже если бы можно было дождаться этого, у человека нет практической возможности выбрать подходящий момент, в который снова вставить стену. Теорема Пуанкаре о возвращении дает решение парадокса Лошмидта. Если бы изолированную термодинамическую систему можно было контролировать на протяжении все большего числа кратных среднему времени повторения Пуанкаре, термодинамическое поведение системы стало бы инвариантным по отношению к обращению времени.

демон Максвелла
Джеймс Клерк Максвелл представил себе один контейнер, разделенный на две части, A и B. Обе части заполнены одним и тем же газом при одинаковых температурах и размещены рядом друг с другом, разделены стеной.Наблюдая за молекулами с обеих сторон, воображаемый демон охраняет микроскопический люк в стене. Когда молекула со скоростью выше средней из A летит к люку, демон открывает его, и молекула летит из A в B. Средняя скорость молекул в B будет увеличиваться, пока в A в среднем они замедлятся. Поскольку средняя скорость молекул соответствует температуре, температура в A уменьшается, а в B увеличивается, что противоречит второму закону термодинамики.
Один ответ на этот вопрос был предложен в 1929 году Лео Сцилардом, а затем Леоном Бриллюэном. Сцилард указал, что реальный демон Максвелла должен иметь какие-то средства измерения молекулярной скорости и что получение информации потребует затрат энергии.
«демон» Максвелла неоднократно изменяет проницаемость стены между A и B. Поэтому он выполняет термодинамические операции в микроскопическом масштабе, а не просто наблюдает за обычными спонтанными или естественными макроскопическими термодинамическими процессами.
Цитаты
Я думаю, что закон, согласно которому энтропия всегда увеличивается, занимает высшее положение среди законов Природа. Если кто-то укажет вам, что ваша любимая теория вселенной не согласуется с уравнениями Максвелла — тогда это будет хуже для уравнений Максвелла. Если наблюдение противоречит этому — что ж, экспериментаторы иногда ошибаются. Но если окажется, что ваша теория противоречит второму закону термодинамики, я не могу дать вам никакой надежды; ему ничего не остается, как рухнуть в глубочайшем унижении.
— Сэр Артур Стэнли Эддингтон, Природа физического мира (1927)
Было почти столько же формулировок второго закона, сколько и это обсуждалось.
— Философ / Физик PW Бриджмен, (1941)
Клаузиус является автором сибиллического высказывания: «Энергия Вселенной постоянна; энтропия Вселенной стремится к максимуму». Цели континуальной термомеханики не ограничиваются объяснением «вселенной», но в рамках этой теории мы можем легко вывести явное утверждение, в некотором роде напоминающее Клаузиуса, но относящееся только к скромному объекту: изолированному телу конечных размеров
— Truesdell, C., Muncaster, RG (1980). Основы кинетической теории Максвелла простого одноатомного газа, рассматриваемого как раздел рациональной механики, Academic Press, Нью-Йорк, ISBN 0-12-701350-4 , с. 17.
См. Также
- Неравенство Клаузиуса-Дюгема
- Теорема флуктуаций
- Тепловая смерть Вселенной
- История термодинамики
- Равенство Ярзинского
- Законы термодинамики
- Термодинамика с максимальной энтропией
- Квантовая термодинамика
- Размышления о движущей силе огня
- Релятивистская теплопроводность
- Тепловой диод
- Термодинамическое равновесие
Ссылки
Источники
| Thermodynamics | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|

The classical Carnot heat engine |
|||||||||||||||||||||
|
Branches
|
|||||||||||||||||||||
|
Laws
|
|||||||||||||||||||||
|
Systems
|
|||||||||||||||||||||
|
System properties Note: Conjugate variables in italics
|
|||||||||||||||||||||
|
Material properties
|
|||||||||||||||||||||
|
Equations
|
|||||||||||||||||||||
|
Potentials
|
|||||||||||||||||||||
|
|||||||||||||||||||||
|
Scientists
|
|||||||||||||||||||||
|
|||||||||||||||||||||
|
Carnot’s theorem, developed in 1824 by Nicolas Léonard Sadi Carnot, also called Carnot’s rule, is a principle that specifies limits on the maximum efficiency any heat engine can obtain. The efficiency of a Carnot engine depends solely on the temperatures of the hot and cold reservoirs.
Carnot’s theorem states that all heat engines between two heat reservoirs are less efficient than a Carnot heat engine operating between the same reservoirs. Every Carnot heat engine between a pair of heat reservoirs is equally efficient, regardless of the working substance employed or the operation details.
The maximum efficiency is the ratio of the temperature difference between the reservoirs and the temperature of the hot reservoir, expressed in the equation 
where TC and TH are the absolute temperatures of the cold and hot reservoirs, respectively, and the efficiency 
Carnot’s theorem is a consequence of the second law of thermodynamics. Historically, it was based on contemporary caloric theory, and preceded the establishment of the second law.
Proof
An impossible situation: A heat engine cannot drive a less efficient (reversible) heat engine without violating the second law of thermodynamics.
The proof of the Carnot theorem is a proof by contradiction, or reductio ad absurdum, as illustrated by the figure showing two heat engines operating between two reservoirs of different temperature. The heat engine with more efficiency (


It is generally agreed that this is impossible because it violates the second law of thermodynamics.
We begin by verifying the values of work and heat flow depicted in the figure. First, we must point out an important caveat: the engine with less efficiency (

By restricting our discussion to cases where engine (






The figure is also consistent with the definition of efficiency as 
It may seem odd that a hypothetical heat pump with low efficiency is being used to violate the second law of thermodynamics, but the figure of merit for refrigerator units is not efficiency, 
which is 

Having established that the heat flow values shown in the figure are correct, Carnot’s theorem may be proven for irreversible and the reversible heat engines.
Reversible engines
To see that every reversible engine operating between reservoirs 


- All reversible engines that operate between the same two heat reservoirs have the same efficiency.
This is an important result because it helps establish the Clausius theorem, which implies that the change in entropy is unique for all reversible processes.,
over all paths (from a to b in V-T space). If this integral were not path independent, then entropy, S, would lose its status as a state variable.
Irreversible engines
If one of the engines is irreversible, it must be the (M) engine, placed so that it reverse drives the less efficient but reversible (L) engine. But if this irreversible engine is more efficient than the reversible engine, (i.e., if 
- No irreversible engine is more efficient than the Carnot engine operating between the same two reservoirs.
Definition of thermodynamic temperature
- Main articles: Thermodynamic temperature#Definition of thermodynamic temperature
The efficiency of the engine is the work divided by the heat introduced to the system or
-
(1)
where wcy is the work done per cycle. Thus, the efficiency depends only on qC/qH.
Because all reversible engines operating between the same heat reservoirs are equally efficient, all reversible heat engines operating between temperatures T1 and T2 must have the same efficiency, meaning the efficiency is a function only of the two temperatures:
-
(2)
In addition, a reversible heat engine operating between temperatures T1 and T3 must have the same efficiency as one consisting of two cycles, one between T1 and another (intermediate) temperature T2, and the second between T2 and T3. This can only be the case if
Specializing to the case that 
Therefore, if thermodynamic temperature is defined by
then the function viewed as a function of thermodynamic temperature, is
and the reference temperature T1 has the value 273.16. (Of course any reference temperature and any positive numerical value could be used—the choice here corresponds to the Kelvin scale.)
It follows immediately that
-
(3)
Substituting Equation 3 back into Equation 1 gives a relationship for the efficiency in terms of temperature:
-
(4)
Applicability to fuel cells and batteries
Since fuel cells and batteries can generate useful power when all components of the system are at the same temperature (

References

|
This page uses content that though originally imported from the Wikipedia article Carnot’s_theorem_(thermodynamics) might have been very heavily modified, perhaps even to the point of disagreeing completely with the original wikipedia article. The list of authors can be seen in the page history. The text of Wikipedia is available under the Creative Commons Licence. |
















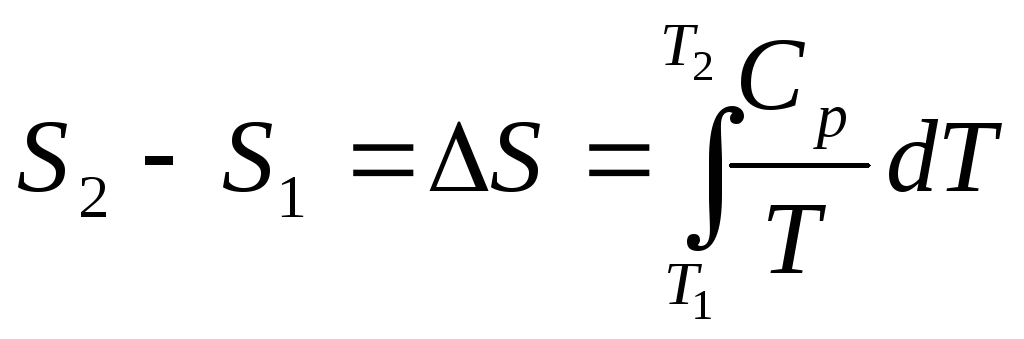
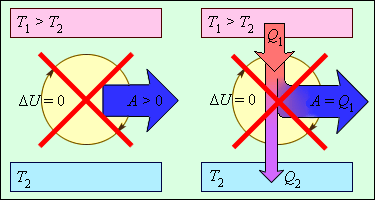
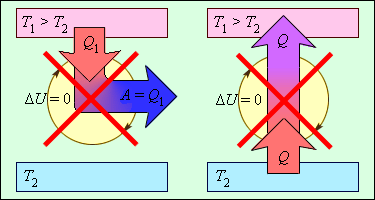
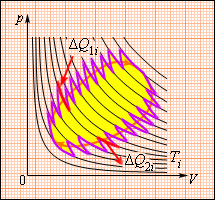
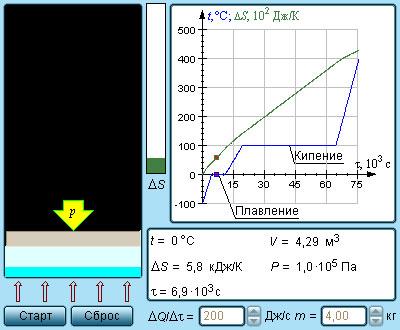
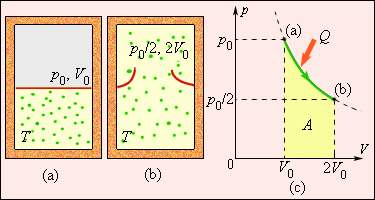
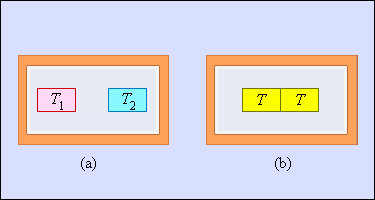




















 эквивалентно d E + δ wu ≤ 0 { displaystyle dE + delta w_ {u} leq 0 }
эквивалентно d E + δ wu ≤ 0 { displaystyle dE + delta w_ {u} leq 0 }



 с S ˙ я ≥ 0 { displaystyle { dot {S}} _ {i} geq 0}
с S ˙ я ≥ 0 { displaystyle { dot {S}} _ {i} geq 0}
 с S ˙ я ≥ 0 { displaystyle { dot {S}} _ {i} geq 0}
с S ˙ я ≥ 0 { displaystyle { dot {S}} _ {i} geq 0} — тепловой поток в систему.
— тепловой поток в систему. — температура в точке, где тепло входит в систему.
— температура в точке, где тепло входит в систему. с S ˙ i ≥ 0 { displaystyle { dot {S}} _ {i} geq 0}
с S ˙ i ≥ 0 { displaystyle { dot {S}} _ {i} geq 0}![S = k _ { mathrm B} ln left [ Omega left (E right) right] ,](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb924dffe4f5c2c580cd40461cf5bfc5159ac881)

![frac {1} {k _ { mathrm B} T} Equiv beta Equiv frac {d ln left [ Omega left (E right) right]} {dE}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e720432da60639a2f9cdcefb4ac56845da4f36b0)





































