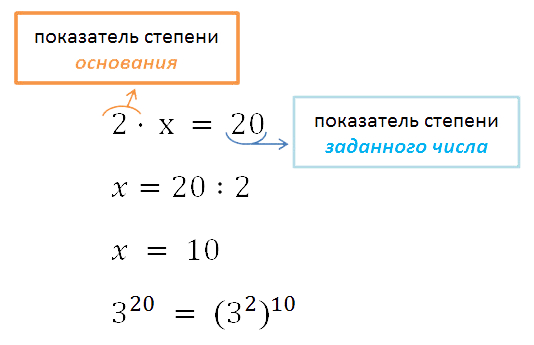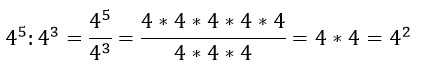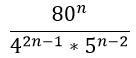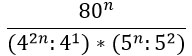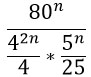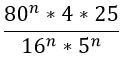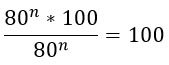5 формул степеней 7 класс алгебра

Напоминаем, что в данном уроке разбираются свойства степеней
с натуральными показателями и нулём.
Степени с рациональными показателями и их свойства будут рассмотрены в уроках
для 8 классов.

Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют
упрощать вычисления в примерах со степенями.

Свойство № 1
Произведение степеней

Данное свойство степеней также действует на произведение трёх и более степеней.

Примеры.

• Упростить выражение.
  
  b · b² · b³ · b⁴ · b⁵ =
  b ^{1 + 2 + 3 + 4 + 5} = b¹⁵
• Представить в виде степени.
  
  
  6¹⁵ · 36 = 6¹⁵ · 6² = 6¹⁵ · 6² =
  6¹⁷
• Представить в виде степени.
  
  
  (0,8)³ · (0,8)¹² = (0,8)^{3 + 12} = (0,8)¹⁵

Свойство № 2
Частное степеней

Примеры.

• Записать частное в виде степени
  
  (2b)⁵ : (2b)³ = (2b)^{5 − 3} = (2b)²
• Вычислить.
  

  =
  11^{3 − 2} · 4 ^{2 − 1} = 11 · 4 = 44

• Пример. Решить уравнение. Используем свойство частного степеней.
  
  
  3⁸ : t = 3⁴

  t = 3⁸ : 3⁴

  t = 3^{8 − 4}

  t = 3⁴

  
  Ответ: t = 3⁴ = 81

Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.

• Пример. Упростить выражение.
  
  
  4^{5m + 6} · 4^{m + 2} : 4^{4m + 3} =
  4^{5m + 6 + m + 2} : 4^{4m + 3} =
  4^{6m + 8 − 4m − 3} = 4^{2m + 5}
• Пример. Найти значение выражения, используя свойства степени.
  

  =
  =

  =

  =

  =

  2^{11 − 5} = 2 ⁶ = 64
  

Свойство № 3
Возведение степени в степень

• Пример.
  (a⁴)⁶ = a^{4 · 6} = a²⁴
• Пример. Представить 3²⁰ в виде степени с основанием
  3².

  По свойству возведения степени в степень известно, что при возведении
  в степень показатели перемножаются, значит:

  

Свойства 4
Степень произведения

• Пример 1.
  (6 · a² · b³ · c )² =
  6² · a^{2 · 2} · b^{3 · 2}
  · с ^{1 · 2} = 36 a⁴ · b⁶
  · с ²
  
• Пример 2.
  
  (−x² · y)⁶ =

  ( (−1)⁶ · x^{2 · 6} · y^{1 · 6}) =

  x¹² · y⁶
  

То есть, чтобы перемножить степени с одинаковыми
показателями можно перемножить основания, а показатель степени оставить неизменным.

• Пример. Вычислить.
  2⁴ · 5⁴ = (2 · 5)⁴ =
  10⁴ = 10 000
• Пример. Вычислить.
  0,5¹⁶ · 2¹⁶ = (0,5 · 2)¹⁶ =
  1

В более сложных примерах могут встретиться случаи, когда умножение и деление
надо выполнить над степенями с разными основаниями и разными показателями.
В этом случае советуем поступать следующим образом.

Например,

4⁵ · 3² = 4³ ·
4² · 3² = 4³ · (4 · 3)² =

64 · 12² = 64 · 144 = 9216

Пример возведения в степень десятичной дроби.

4²¹ · (−0,25)²⁰ = 4 · 4 ²⁰ ·
(−0,25) ²⁰ = 4 · (4 · (−0,25))²⁰ = 4 · (−1)²⁰ =
4 · 1 = 4

Свойства 5
Степень частного (дроби)

• Пример. Представить выражение в виде частного степеней.
  
  (5 : 3)¹² = 5¹² : 3¹²

Напоминаем, что частное можно представить в виде дроби. Поэтому
на теме
возведение дроби в степень
мы остановимся более подробно на следующей странице.

---

Ваши комментарии

Оставить комментарий:

---

Степени и их свойства

Данная тема очень легкая, если выучить все свойства степеней. Они, кстати, достаточно просты для запоминания.

Перед тем, как перейти в свойствам степеней, разберемся, что такое степень.

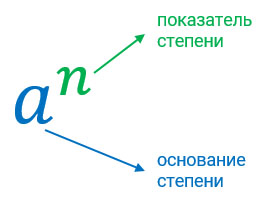
Степень — это произведение одинаковых множителей, состоящая из основания и показателя. Наглядно это можно рассмотреть на рисунке ниже.

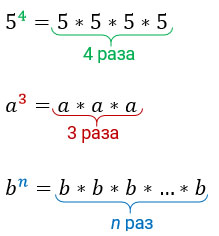
Показатель степени показывает (масло масляное) сколько раз мы умножаем основание на себя. Это очень хорошо проглядывается на следующих примерах:

Вроде бы ничего сложного нет, правда?

Что ж, время перейти к свойствам.

Свойства степеней.

1. Любое число в первой степени равно самому себе: a¹ = a.

Сразу рассмотрим примеры.

2¹ = 2;

(-10)¹ = -10;

0¹ = 0.

2. Любое число в нулевой степени равно 1: а⁰ = 1.

Примеры:

2⁰ = 1;

(-3)⁰ = 1;

0⁰ = 1.

3. Единица в любой степени равна 1: 1ⁿ = 1.

4. При умножении степеней с одинаковыми основаниями показатели складываются: aⁿ · a^m = a^{n + m}.

Почему так?

Это свойство легко доказать на числовом примере.

2³ · 2² = 2 · 2 · 2 · 2 · 2 = 2⁵.

Конечно, так никто не расписывает, а сразу пользуется готовой формулой. Вот еще несколько примеров:

3⁴ · 3⁹ · 3¹⁵ = 3^{4 + 9 + 15} = 3²⁸;

(-2)³ · (-2)⁴ = (-2)^{3 + 4} = (-2)⁷.

5. При делении степеней с одинаковыми основаниями показатели вычитаются: aⁿ : a^m = a^{n — m} (a ≠ 0).

Доказывается эта формула тоже очень просто с помощью числового примера: три четверки из числителя сокращаем с тремя четверками из знаменателя и остаются две четверки в числителе, т.е. 4².

Еще парочка примеров:

15¹⁰ : 15³ : 15⁵ = 15^{10 — 3 — 5} = 10²;

(-3)¹¹ : (-3)⁵ = (-3)^{11 — 5} = (-3)⁶.

6. При возведении степени в степень показатели умножаются: (аⁿ)^m = a^nm.

Примеры:

(2²)³ = 2^{2 · 3} = 2⁶;

(5³)¹⁰ = 5^{3 · 10} = 5³⁰.

7. При возведении произведения в степень каждый множитель возводится в эту степень: (ab)ⁿ = aⁿbⁿ.

Примеры:

(5 · 4)² = 5² · 4²;

(2 · 3  · 4 · 5)^а = 2^а · 3^а · 4^а ·5^а.

8. Чтобы возвести дробь в степень надо и числитель, и знаменатель возвести в эту степень:.

Пример:

9. Степень с дробным показателем можно представить в виде корня некоторой степени по формуле (а > 0, n ≥ 2).

Пример:

10. Чтобы возвести число, отличное от нуля, в степень с отрицательным показателем надо взять число, обратное данному, и возвести его в ту же степень, только без минуса: (a ≠ 0).

Это же правило работает и для дробей:  (a ≠ 0, b ≠ 0).

Примеры:

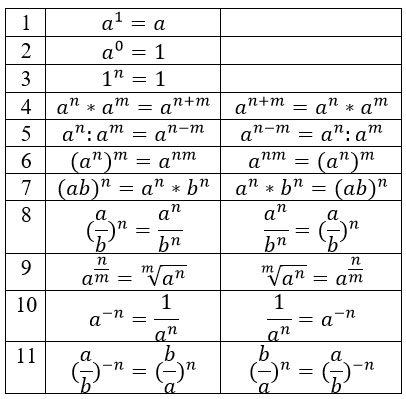
Все эти свойства срабатывают как в одну сторону, так и в другую. Соберем их в аккуратную табличку.

Напоследок, разберем пример, который может встретиться во второй части ОГЭ по математике. Он, конечно, не охватывает сразу все формулы — только несколько из них.

Нам нужно сократить такую дробь:

Преобразуем знаменатель дроби, дважды использовав формулу по номером 5 из второго столбика таблицы.

Получившиеся частные в знаменателе запишем в виде дробей.

Получилась трехярусная дробь (можно произведение дробей в знаменателе переписать под одну черту). Нижний ярус этой дроби перейдет в верхний. Это не магия вне Хогвартса, но описывать эти преобразования текстом очень грустно. Если коротенько, то при делении на дробь мы ее переворачиваем и получается, что знаменатель заползает наверх 🙂

К тому же здесь можно воспользоваться свойством 6 из второго столбика и 4²ⁿ превратится в 16ⁿ.

Переходим к финалу. Преобразуем знаменатель по свойству 7 из второго столбика таблицы (снова) и, наконец-таки, сокращаем дробь!

Успехов в учебе!

С уважением, Васильева Анна.

Свойства степени с натуральным показателем

Примеры

Пример 1. Запишите в виде степени с основанием 2

а) $ 2cdot4cdot16 = 2^1cdot2^2cdot2^4 = 2^{1+2+4} = 2^7 $

б) $4cdot 32^2 = 2^2 cdot (2^5)^2 = 2^2cdot2^{5cdot2} = 2^{2+10} = 2^{12}$

в) $4cdot8:32 = 2^2 cdot 2^3:2^5 = 2^{2+3-5} = 2^0$

г) $ frac{2^{10}}{(2^3)^2} = frac{2^{10}}{2^{3 cdot 2}} = 2^{10-6} = 2^4 $

Пример 2. Запишите в виде степени:

а) $ left(-frac{3}{7}right)^5 : left(-frac{3}{7}right)^3 = left(-frac{3}{7}right)^{5-3} = left(-frac{3}{7}right)^2 $

б) $ y^{22}: (y^2)^5 = y^{22}: y^{2cdot5} = y^{22-10} = y^{12} $

в) $ (a+2b)^14:(a+2b)^8 = (a+2b)^{14-8} = (a+2b)^6 $

г) $ (3a+5)^2cdot(3a+5)^7:(3a+5)^4 = (3a+5)^{2+7-4} = (3a+5)^5 $

Пример 3. Найдите значение выражения:

а) $ frac{7cdot3^3}{3^2} = 7cdot3^{3-2} = 7cdot3 = 21 $

б) $ frac{2^4cdot3^3}{4cdot9} = frac{2^4}{2^2} cdot frac{3^3}{3^2} = 2^{4-2}cdot3^{3-2} = 2^2cdot3^1 = 4cdot3 = 12$

в) $ frac{5^6cdot5}{25cdot125} = frac{5^{6+1}}{5^2cdot5^3} = frac{5^7}{5^5} = 5^{7-5} = 5^2 = 25 $

г) $ frac{11^3cdot4^7}{11^2cdot16cdot64} = frac{11^3}{11^2} cdot frac{4^7}{4^2cdot4^3} = 11^{3-2} cdot 4^{7-5} = 11^1cdot4^2 = 11cdot16 = 176 $

д) $ left(frac{3^5}{10^2}right)^2 cdot left(frac{2}{5}right)^5 cdot left(frac{5}{3}right)^4 = frac{(3^5 )^2}{((5cdot2)^2)^2}^2 cdot frac{2^5}{3^5} cdot frac{5^4}{3^4} = frac{3^{10}}{5^4 cdot 2^4} cdot frac{2^5 cdot 5^4}{3^{5+4}} = frac{3^{10}}{3^9} cdot frac{2^5}{2^4} cdot frac{5^4}{5^4} = frac{3^{10}}{3^9} cdot frac{2^5}{2^4} cdot frac{5^4}{5^4} = 3^1 cdot 2^1 cdot 5^0 = 6 $

е) $ left(frac{5}{3}right)^5 cdot left(1frac{4}{5}right)^2 cdot (1,5)^2 = frac{5^5}{3^5} cdot left(frac{9}{5}right)^2 cdot left(frac{3}{2}right)^2 = frac{5^5}{3^5} cdot frac{(3^2 )^2}{5^2} cdot frac{3^2}{2^2} = frac{5^5}{5^2} cdot frac{3^{4+2}}{3^5} cdot frac{1}{2^2} = frac{5^3cdot3}{2^2} = frac{725}{4} = 181 frac{1}{4} $

ж) $ frac{3^3cdot7{22}-3^2cdot7^{21}}{49^{10}} = frac{7{21}cdot3^2(3cdot7-1)}{(7^2)^{10}} = 7^{21-20}cdot3^2cdot20 = 7cdot9cdot20 = 1260 $

з) $ frac{(7^3cdot5^2-7^2cdot5^3 )cdot77}{(11cdot49)^2} = frac{7^2cdot5^2 (7-5)cdot11cdot7}{11^2cdot(7^2)^2} = frac{5^2cdot2}{11cdot7} = frac{50}{77} $

Пример 4. Возведите в степень выражение:

а) $ (a^2 b^3)^4 = (a^2)^4cdot(b^3)^4 = a^{2cdot4} cdot b^{3cdot4} = a^8 b^12 $

б) $ (-2x^5 y)^4 = (-2)^4 cdot (x^5)^4 cdot y^4 = 16x^{20}y^4 $

в) $ left(frac{10x^2}{y^3}right)^5 = left(frac{10^5cdot(x^2)^5}{(y^3 )^5}right)^5 = frac{100000x^{10}}{y^15} $

г) $ left(-frac{3y^8}{m^4 n}right)^3 = -frac{3^3cdot(y^8 )^3}{(m^4 )^3cdot n^3} = -frac{27y^{24}}{m^{12} n^3} $

Пример 5. Представьте в виде степени и вычислите:

а) $ frac{3^{10}cdot6^{10}}{2^{10}cdot9^{10}} = frac{(3cdot6)^{10}}{(2cdot9)^{10}} = frac{18^{10}}{18^{10}} = 1 $

б) $ 3^{n+2}:3^{n-1} = 3^{(n+2)-(n-1)} = 3^3 = 27 $

в) $ frac{4^{20}}{8^{13}} = frac{(2^2)^{20}}{(2^3)^{13}} = frac{2^{40}}{2^{39}} = 2^{40-39} = 2 $

г) $ 0,125^{10}cdot8^{10} = (0,125cdot8)^{10} = 1^{10} = 1 $

Пример 6. Сравните значения выражений:

а) $ 2,5^3 и 2,5^0 $

$ left. begin{array}{l} 2,5^3 = left(frac{5}{2}right)^3 = frac{125}{8} gt 1 \ 2,5^0 = 1 end{array} right} Rightarrow 2,5^3 gt 2,5^0 $

б) $ 0,7^3 и 0,7^0 $

$ left. begin{array}{l} 0,7^3 = left(frac{7}{10}right)^3 = frac{343}{1000} lt 1 \ 0,7^0 = 1 end{array} right} Rightarrow 0,7^3 gt 0,7^0 $

в) $ (-0,8)^5 и 0,8^0 $

$ left. begin{array}{l} (-0,8)^5 lt 0 \ 0,8^0 = 1 gt 0 end{array} right} Rightarrow (-0,8)^5 lt 0,8^0 $

Пример 7*. Какое из чисел больше?

а) $ 10^{20}$ или $ 20^{10} $

$ 10^{20} = (10^2)^{10} = 100^{10} $

$ 100 gt 20 Rightarrow 100^{10} gt 20^{10} Rightarrow 10^{20} gt 20^{10} $

б) $ 6^{20}$ или $2^{60} $

$2^{60} = (2^3)^{20} = 8^{20}$

$ 6 lt 8 Rightarrow 6^{20}lt 8^{20} Rightarrow 6^{20} lt 2^{60} $

в) $ 2^{300}$ или $3^{200} $

$ 2^{300} = (2^3)^{100} = 8^{100} $

$ 3^{200} = (3^2)^{100} = 9^{100} $

$ 8lt 9 Rightarrow 8^{100} lt 9^{100} Rightarrow 2^{300} lt 3^{200} $

«Алгебра 7 класс Все формулы и определения» — это краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского) — М.: Просвещение.

---

Выражения и их преобразования

☑ 1. Степенью числа а с натуральным показателем n, большим 1, называют произведение n множителей, каждый из которых равен а:
Степенью числа а с показателем 1 называют само число а:  а¹ = а.
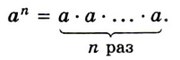
Степень числа а ≠ 0 с показателем 0 равна 1:  а⁰ = 1.

☑ 2. Свойства степеней с натуральными показателями:

 а^m • аⁿ = а^m+n

При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.

а^m : аⁿ = а^m-n, где а ≠ 0, m ≥ n

(а^m)ⁿ = а^mn

При возведении степени в степень основание оставляют прежним, а показатели перемножают.

(ab)ⁿ = аⁿbⁿ

При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.

☑ 3. Одночленами называют произведения чисел, переменных и их степеней, а также сами числа, переменные и их степени. Например, 5а²х, –3а²b³, 4, х, у⁵ — одночлены.

 Степенью одночлена называют сумму показателей степеней всех переменных, входящих в одночлен. Например, степень одночлена –8а²b⁴ равна 6.

☑ 4. Многочленом называют сумму одночленов. Например, 3х⁵ – 4х² + 1, 7a³b – ab² + ab + 6—многочлены. Одночлены считают многочленами, состоящими из одного члена.

Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Например, степень многочлена 5х³у + 3х²у⁵ + ху равна степени одночлена 3х²у⁵, т. е. равна 7.

Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.

☑ 5. При сложении многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки. Например,

(3аb + 5с²) + (ab – с²) = 3ab + 5с² + ab – с² = 4аb + 4с²

При вычитании многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки. Например,

(6x² – у) – (2x² – 8у) = 6х² – у – 2х² + 8у = 4х² + 7у

Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Например,

а² (3аb – b³ + 1) = 3а³b – а²b³ + а²

Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. Например,

(5х – 1)(3х + 2) = 15x² – Зx + 10x – 2 = 15x² + 7x – 2

☑ 6. Формулы сокращённого умножения:

(а + b)² = а² + 2аb + b²

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.

(а – b)² = а² – 2аb + b²

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.

(а + b)³ = а³ + 3а²b + 3ab² + b³

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

(а – b)³ = а³ – 3а²b + Заb² – b³

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(а – b)(а + b) = а² – b²

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

а³ + b³ = (а + b)(a² – аb + b²)

Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

а³ – b³ = (а – b)(a² + ab + b²)

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

☑ 7. Разложением многочлена на множители называют представление многочлена в виде произведения многочленов.

Для разложения многочленов на множители применяют вынесение общего множителя за скобки, группировку, формулы сокращённого умножения. Например, многочлен 5х³ – х²у можно разложить на множители, вынеся за скобки х²:

5х³ – х²у = х² (5х – у).

Многочлен 3х – 3у – ах + ау можно разложить на множители, используя способ группировки:

3х – 3у – ах + ау = (3x – 3у) – (ах – ау) = 3(х – у) – а (х – у) = (х – у)(3 – а).

Многочлен а⁴ – 25x² можно разложить на множители, используя формулу разности квадратов двух выражений:

а⁴ – 25x² = (а²)² – (5x)² = (а² – 5x)(а² + 5x).

Иногда многочлен удаётся разложить на множители, применив последовательно несколько способов.

Алгебра 7 класс Все формулы

Уравнения

☑ 8. Корнем уравнения с одной переменной называют значение переменной, при котором уравнение обращается в верное равенство. Например, число 8 — корень уравнения 3x + 1 = 5х – 15, так как верно равенство 3 • 8 + 1 = 5 • 8 – 15.

Решить уравнение с одной переменной — значит найти все его корни или доказать, что корней нет.

☑ 9. Уравнения с одной переменной, имеющие одни и те же корни, называют равносильными. Например, уравнения x² = 25 и (х + 5)(х – 5) = 0 равносильны. Каждое из них имеет два корня: –5 и 5. Уравнения, не имеющие корней, также считают равносильными.

При решении уравнений с одной переменной используются следующие свойства:

• если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;
• если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

☑ 10. Линейным уравнением с одной переменной называют уравнение вида ах = b, где х — переменная, а и b — числа.

Если а ≠ 0, то уравнение ах = b имеет единственный корень b/a.

Например, уравнение 7х = 2 имеет корень 2/7.

Если а = 0 и b ≠ 0, то уравнение ах = b не имеет корней. Например, уравнение 0 • х = 7 не имеет корней.

Если а = 0 и b = 0, то корнем уравнения ах = b является любое число.

☑ 11. Решением уравнения с двумя переменными называют пару значений переменных, обращающую это уравнение в верное равенство. Например, пара чисел х = -1, у = 4 — решение уравнения 5х + 3у = 7.

Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения с двумя переменными, не имеющие решений, также считают равносильными.

В уравнении с двумя переменными можно переносить слагаемые из одной части в другую, изменяя их знаки, и обе части уравнения можно умножать или делить на одно и то же число, не равное нулю. При этом получаются уравнения, равносильные исходному.

☑ 12. Линейным уравнением с двумя переменными называют уравнение вида ах + by = с, где х и у — переменные, а, b и с — числа.

☑ 13. Графиком уравнения с двумя переменными называют множество точек координатной плоскости, координаты которых являются решениями этого уравнения.

Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.

☑ 14. Решением системы уравнений с двумя переменными называют пару значений переменных, обращающую каждое уравнение системы в верное равенство. Например, пара чисел х = 7, у = –1 — решение системы
так как является верным каждое из равенств   7 + (–1) = 6   и   2 • 7 – (–1) = 15.

Решить систему уравнений — значит найти все её решения или доказать, что решений нет.

Системы уравнений с двумя переменными, имеющие одни и те же решения, называют равносильными. Системы, не имеющие решений, также считают равносильными.

☑ 15. Для решения систем линейных уравнений с двумя переменными используются графический способ, способ подстановки, способ сложения.

При графическом способе строят графики линейных уравнений (прямые) и анализируют их расположение:

• если прямые совпадают, то система имеет бесконечно много решений, причём координаты любой точки прямой являются решением системы;
• если прямые параллельны, то система не имеет решений; если прямые пересекаются, то система имеет единственное решение, причём координаты точки пересечения прямых являются решением системы.

При решении системы двух линейных уравнений с двумя переменными способом подстановки поступают следующим образом:

• выражают из какого–либо уравнения системы одну переменную через другую;
• подставляют в другое уравнение системы вместо этой переменной полученное выражение;
• решают получившееся уравнение с одной переменной; подставляют значение найденной переменной в одно из уравнений и находят соответствующее значение другой переменной.

При решении системы двух линейных уравнений с двумя переменными способом сложения поступают следующим образом:

• умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали в уравнениях противоположными числами;
• складывают почленно левые и правые части уравнений системы; решают получившееся уравнение с одной переменной; подставляют значение найденной переменной в одно из уравнений и находят соответствующее значение другой переменной.

Алгебра 7 класс Все формулы

Функции

☑ 16. Функциональная зависимость, или функция, — это такая зависимость между двумя переменными, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной.

Независимую переменную иначе называют аргументом, а о зависимой переменной говорят, что она является функцией этого аргумента. Все значения, которые принимает независимая переменная, образуют область определения функции.

Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

☑ 17. Линейной функцией называют функцию, которую можно задать формулой вида у = kx + b, где х — независимая переменная, k и b — числа.

Графиком линейной функции у = kx + b является прямая. Число k называют угловым коэффициентом прямой, являющейся графиком функции у = kx + b.

Если k ≠ 0, то график функции у = kx + b пересекает ось х; если k = 0 и b ≠ 0, то прямая — график функции у = kx + b, параллельна оси х; если k = 0 и b = 0, то график функции совпадает с осью х.

Графики двух линейных функций пересекаются, если их угловые коэффициенты различны, и параллельны, если их угловые коэффициенты одинаковы.

Линейную функцию, задаваемую формулой у = kx при k ≠ 0, называют прямой пропорциональностью.

 График прямой пропорциональности есть прямая, проходящая через начало координат. При k > 0 график расположен в первой и третьей координатных четвертях, а при k < 0 — во второй и четвёртой координатных четвертях.

☑ 18. График функции у = х² — парабола. Этот график проходит через начало координат и расположен в первой и второй координатных четвертях. Он симметричен относительно оси у.

График функции у = х³ проходит через начало координат и расположен в первой и третьей координатных четвертях. Он симметричен относительно начала координат.

Статистические характеристики

 ☑ Средним арифметическим ряда чисел называют частное от деления суммы этих чисел на число слагаемых.

 Модой ряда чисел называют число, которое встречается в данном ряду чаще других. Ряд чисел может иметь более одной моды или не иметь моды совсем.

 Медианой упорядоченного ряда чисел с нечётным числом членов называют число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называют среднее арифметическое двух чисел, записанных посередине.

Например, медиана ряда чисел  17, 21, 27, 29, 32, 37, 41 равна 29, а медиана ряда чисел  28, 43, 54, 56, 58, 62 равна 55.

 Медианой произвольного ряда чисел называют медиану соответствующего упорядоченного ряда.

Размахом ряда чисел называют разность между наибольшим и наименьшим из этих чисел.

---

Вы смотрели Конспект «Алгебра 7 класс Все формулы и определения» — краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского). Выберите дальнейшие действия:

• Посмотреть Краткий курс Геометрии за 7 класс 
• Вернуться к Списку конспектов по алгебре
• Онлайн-учебник алгебры 7 кл УМК Мерзляк Полонский Якир (с ответами)
• Онлайн-учебник алгебры 7 кл УМК Макарычев (с ответами)
• Онлайн-учебник алгебры 7 кл УМК Мордкович (с ответами)
• Онлайн-учебник алгебра 8 класс УМК Макарычев (с ответами)

Алгебра

7 класс

Урок № 2

Степень числа

Перечень вопросов, рассматриваемых в теме:

Понятие степени числа.

Свойства степеней.

Тезаурус

Степенью числа a с натуральным показателем n, бóльшим 1, называется произведение n одинаковых множителей, каждый из которых равен числу a.

Свойства степеней:

Произведение степеней с одним и тем же показателем равно степени с тем же показателем и основанием, равным произведению оснований.

Произведение степеней с одним и тем же основанием – это степень с тем же основанием и показателем, равным сумме показателей этих степеней.

Степень степени числа равна степени того же числа с показателем, равным произведению показателей этих степеней.

Основная литература:

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

Дополнительная литература:

1. Макарычев Ю. Н. Алгебра: 7 класс. // Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. – М.: Просвещение, 2019. – 256 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение.

Произведение шести множителей, каждый из которых равен 8, называют шестой степенью числа 8 и обозначают 8⁶, т.е.

8 ∙ 8 ∙ 8 ∙ 8 ∙ 8 ∙ 8 = 8⁶.

При этом число 8 называют основанием степени, а число 6 – показателем степени.

А теперь давайте сформулируем общее определение степени числа, опираясь на предыдущий пример:

степенью числа a с натуральным показателем n, бóльшим 1, называется произведение n одинаковых множителей, каждый из которых равен числу a.

Запись aⁿ читается как: а в степени n, или n-ая степень числа a.

А вот следующие записи можно произносить по-разному:

a²– её можно произносить «а в квадрате» или «а во второй степени»;

a³ – её можно произносить «а в кубе» или «а в третьей степени».

Стоит отметить, что особые случаи возникают, если показатель степени равен нулю или единице:

степенью числа а с показателем n = 1 является само это число:

a¹ = a;

любое число в нулевой степени равно единице:

a⁰ = 1;

ноль в любой натуральной степени равен нулю:

0ⁿ = 0;

единица в любой степени равна 1:

1ⁿ = 1.

Выражение 0⁰ (ноль в нулевой степени) считают неопределенным.

Примеры. Возведём в степени:

(−91)⁰ = 1

0¹⁴⁴ = 0

1²³⁶ = 1.

При решении задач, нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в степень.

Рассмотрим несколько примеров.

Возведём в степень

2⁵ = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 = 32

2,5³ = 2,5 ∙ 2,5 ∙ 2,5 = 15,625

Основание степени может быть любым числом – положительным, отрицательным или нулём.
При возведении в степень положительного числа получается положительное число.

При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа, в результате может получиться как положительное число, так и отрицательное число. Это зависит от того, чётным или нечётным числом был показатель степени.

Например, (-2)⁵. Ответ будет отрицательным, так как показатель степени, 5- нечётное число. (-2)⁵ = (-2) ∙ (-2) ∙ (-2) ∙ (-2) ∙ (-2) = -32.

(-5)⁴. А вот в этом примере ответ будет положительным, так как показатель степени, 4 – чётное число.

(-5)⁴ = (-5) ∙ (-5) ∙ (-5) ∙ (-5) = 625.

Рассмотрим такой пример: 4² ∙ 5² = 4 ∙ 4 ∙ 5 ∙ 5 = (4 ∙ 5) ∙ (4 ∙ 5) = (4 ∙ 5)² = 20² = 400.

Данный пример подтверждает справедливость следующего свойства степеней:

Произведение степеней с одним и тем же показателем равно степени с тем же показателем и основанием, равным произведению оснований:

aⁿ∙ bⁿ = (a ∙ b)ⁿ

Приведём еще такой пример: 5² ∙ 5⁵ = (5 ∙ 5) ∙ (5 ∙ 5 ∙ 5 ∙ 5 ∙ 5) = 5 ∙ 5 ∙ 5 ∙ 5 ∙ 5 ∙ 5 ∙ 5 = 5⁷.

Этот пример подтверждает справедливость следующего свойства степеней:

Произведение степеней с одним и тем же основанием это степень с тем же основанием и показателем, равным сумме показателей этих степеней, т.е.

aⁿ ∙ a^m = a^n+m

Наконец, рассмотрим равенство:

(7²)³ = (7 ∙ 7)³ = (7 ∙ 7) ∙ (7 ∙ 7) ∙ (7 ∙ 7) = 7 ∙ 7 ∙ 7 ∙ 7 ∙ 7 ∙ 7 = 7⁶.

Это равенство подтверждает справедливость следующего свойства степеней:

Степень степени числа равна степени того же числа с показателем, равным произведению показателей этих степеней, т.е.

(aⁿ)^m = a^n∙m

Разбор решения заданий тренировочного модуля

№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте

Заполните таблицу:

	Число	Основание	Показатель степени
1.	255
2.	1113
3.	1356

Для заполнения пропусков вспомним, что такое основание и показатель степени.

	Число	Основание	Показатель степени
1.	255	25	5
2.	1113	11	13
3.	1356	135	6

№2. Тип задания: Чему равно произведение 5⁴ ∙ 5¹¹ ∙ 4² ∙ 4¹³?

Варианты ответов:

(4 ∙ 5)¹⁵

4¹³ ∙ 5¹⁴

(4 ∙ 5)³⁰

4¹⁵ ∙ 5³⁰

Для решения задания, воспользуемся свойствами степеней: aⁿ∙a^m= a^n+m и aⁿ∙bⁿ= (a ∙ b)ⁿ

5⁴ ∙ 5¹¹ ∙ 4² ∙ 4¹³ = 5¹⁵ ∙ 4¹⁵ = (4 ∙ 5)¹⁵.

Верный ответ: (4 ∙ 5)¹⁵.

Подробности

Категория: Алгебра 7-9 классы

СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ

ОПРЕДЕЛЕНИЕ СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ

Произведение нескольких одинаковых множителей можно записать в виде степени. Например,

 Выражение 5⁷ читают по-разному: «Пять в седьмой степени», «Седьмая степень числа пять», «Степень числа пять с показателем семь».

Определение. Степенью числа а с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен а. Степенью числа а с показателем 1 называется само число а.

Степень числа а с показателем n обозначают так: аⁿ. Выражение аⁿ называют степенью, число а — основанием степени, число n — показателем степени.

По определению степени:

Вообще,

Нахождение значения степени называют возведением в степень. Приведем примеры возведения в степень:

При возведении в степень отрицательного числа может получиться как положительное число, так и отрицательное. Например,

Степень отрицательного числа с четным показателем есть число положительное, так как произведение четного числа отрицательных множителей положительно. Степень отрицательного числа с нечетным показателем есть число отрицательное, так как произведение нечетного числа отрицательных множителей отрицательно.

Квадрат любого числа есть число положительное или нуль, т. е. при любом а.

Вычислим значения нескольких выражений, содержащих степени.

Пример 1. Найдем значение выражения  :

Значит,

Пример 2. Найдем значение выражения

Значит,

УМНОЖЕНИЕ И ДЕЛЕНИЕ СТЕПЕНЕЙ

Выражение а²а³ представляет собой произведение двух степеней с одинаковыми основаниями. Это произведение можно записать в виде степени с тем же основанием:

Значит,

Мы видим, что произведение а²а³ равно степени с тем же основанием и показателем, равным сумме показателей перемножаемых степеней.

Докажем, что для любого числа а и произвольных натуральных чисел m и n

Для этого, используя определение степени и свойства умножения, представим выражение а^mаⁿ сначала в виде произведения множителей, каждый из которых равен а, а затем в виде степени:

Таким образом,

Доказанное равенство выражает свойство произведения степеней. Его называют основным свойством степени. Оно распространяется на произведение трех и более степеней.

Например,

Отсюда следует правило умножения степеней: при умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают.

Приведем примеры:

Выражение а⁷:а³ является частным двух степеней с одинаковыми основаниями. Это частное при можно представить в виде степени с тем же основанием. Действительно, так как , то по определению частного

Мы видим, что частное а⁷:а³ равно степени с тем же основанием и показателем, равным разности показателей делимого и делителя.

Докажем, что для любого числа и произвольных натуральных чисел тип, таких, что ,

Покажем, что .

Действительно, по основному свойству степени

Значит, по определению частного

Итак, при делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

Приведем примеры:

Мы вывели правило деления ат на а^m для случая, когда . Если это правило применить к частному aⁿ:aⁿ, то получится

Степень с нулевым показателем не была определена. Так как при всяком   и любом натуральном n

то считают, что при

Определение. Всякое число (кроме нуля) в нулевой степени равно единице.

 ВОЗВЕДЕНИЕ В СТЕПЕНЬ ПРОИЗВЕДЕНИЯ И СТЕПЕНИ

Выражение является степенью произведения множителей а и b. Это выражение можно представить в виде произведения степеней а и b:

Значит,

Мы видим, что четвертая степень произведения аb равна произведению четвертых степеней множителей а и b.

Докажем, что для любых а и b и произвольного натурального числа n

По определению степени

Сгруппировав отдельно множители а и множители b, получим :

Воспользовавшись определением степени, находим:

Следовательно,

Свойство степени произведения, выраженное равенством , распространяется на степень произведения трех и более множителей. Например,

Отсюда следует правило: (пpu возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.

Выражение есть степень, основание которой само является степенью. Это выражение можно представить в виде степени с основанием а:

В результате возведения степени а⁵ в третью степень мы получили степень с тем же основанием и показателем, равным произведению показателей 5 и 3.

Докажем, что для любого числа а и произвольных натуральных чисел m и n

По определению степени

Согласно основному свойству степени

Заменим сумму  произведением mn.

Тогда получим:

Следовательно,

Из равенства следует правило: при возведении степени в степень основание оставляют тем же, а показатели перемножают.

Свойства степеней, выраженные формулами и , имеют место и для степеней с нулевым показателем (если основания отличны от нуля).