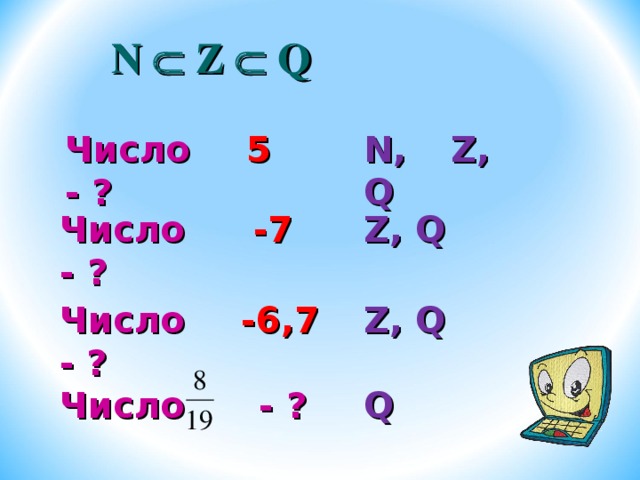По теме: методические разработки, презентации и конспекты
Презентация к уроку алгебры в 8 классе по теме «Квадратные уравнения» Презентация к уроку «Действительные числа»
Презентация к уроку объяснения нового материала по теме «Определение квадратных уравнений» Урок 8 класс.Презентация к уроку закрепления по теме «Действительные числа» в 8 классе….
Урок алгебры 7класс «Степень числа»
Это презентация к уроку алгебры для 7 класса по теме «Степень числа»….
Презентация к уроку по теме «Натуральные числа. Числа великаны»
Предлагаемый материал расширяет понятие о натуральных числах, выводит ученика за рамки школьного учебника…
Презентация к уроку алгебры в 10 классе по теме «Действительные числа»
Данная презентация содержит основные понятия по теме «Действительные числа» и задания для отработки практических навыков и умений….
Технологическая карта урока алгебры в 7 классе по теме «Раскрытие скобок», презентация к уроку алгебры в 7 классе по теме «Раскрытие скобок»
«Раскрытие скобок». Этот материал является подготовительным для решения уравнений новым способом, по программе на его усвоение отводится три часа. Данный урок первый.
Нужно изучить и научиться примен…
презентация к уроку алгебры по теме «Стандртный вид числа»
презентация к уроку алгебры по теме «Стандртный вид числа» 8 класс (Муравин)…
Презентация к уроку алгебры и начала анализа «Комплексные числа» 10 класс
laquo;Комплексные числа – это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием». Г. Лейбниц…
Алгебра. 8 класс.
РАЦИОНАЛЬНЫЕ ЧИСЛА.
« Числа не управляют миром, но они показывают, как управлять им».
( И. Гёте).
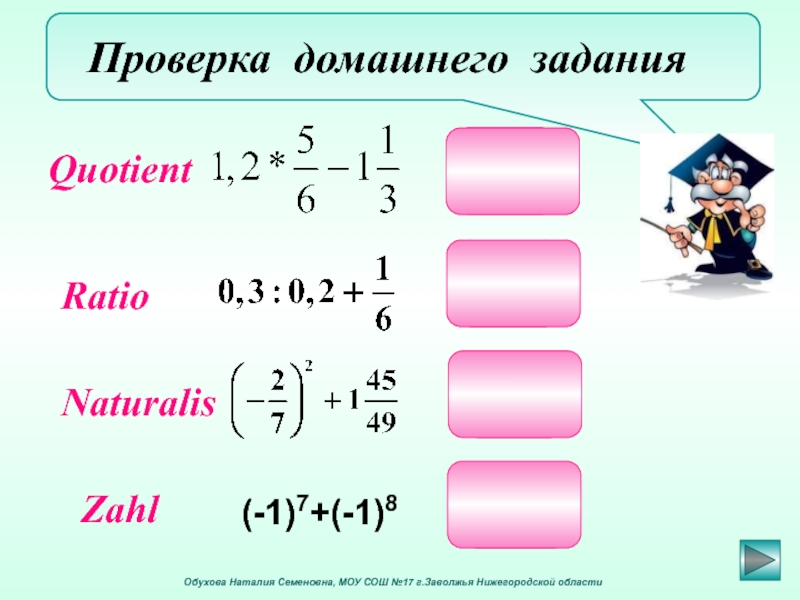
(-1)7+(-1)8
Naturalis
Quotient
Ratio
Zahl
Проверка домашнего задания
Множество чисел, которое можно представить в виде ,
называется множеством рациональных чисел и обозна-
чается- Q первой буквой французского слова Quotient
— «отношение».
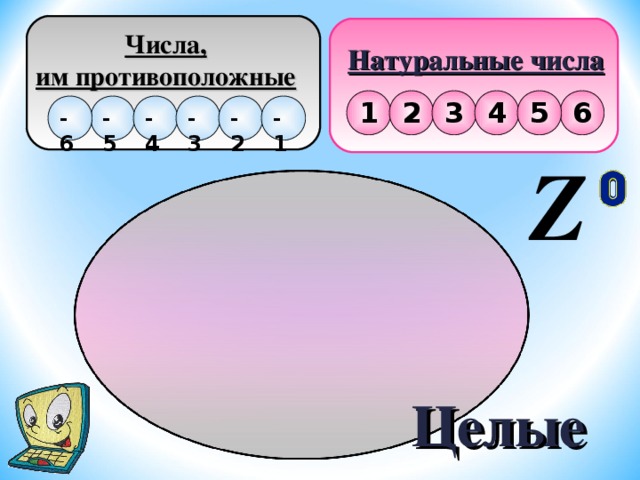
Для счета предметов используются числа , которые называются натуральными. Для обозначения множества натуральных чисел употребляется буква N -первая буква латинского слова Naturalis, «естественный», «натуральный»
Натуральные числа, числа им противоположные
и число нуль, образуют множество целых чисел,
которое обозначается Z — первой буквой
немецкого слова Zahl — «число».
Тема урока:
РАЦИОНАЛЬНЫЕ ЧИСЛА
Цель урока:
систематизировать знания о
рациональных числах;
познакомиться с историей возникновения рациональных чисел;
выделить общее свойство рациональных чисел.
Натуральные числа несут ещё
другую функцию –
характеристика порядка предметов,
расположенных в ряд.
Натуральные числа возникли в силу необходимости вести счет любых предметов.
1 2 3 4 5 6 7 8 9 10…
О натуральном,в смысле естественном,
ряде чисел говорится во «Введении в арифметику» греческого математика
( неопифагорийца) Никомаха из Геразы.
В современном смысле
понятие и термин
«Натуральное число»
встречается у французского
философа и математика Ж.Даламбера (1717-1783)
Натуральные числа
1, 2, 3, 4, 5, 6…
Сумма и произведение натуральных
чисел есть число натуральное.
n — натуральное
Дроби естественно возникли при решении
задач о разделе имущества, измерении
земельных участков, исчислении времени.
Дробные числа
Сумма, произведение и частное
дробных чисел есть число дробное.
1) доли или единичные дроби,
у которых числитель единица,
знаменателем же может быть
любое целое число;
3)дроби общего вида, у которых числители и знаменатели могут быть любыми числами.
2) дроби систематические, у которых
числителями могут быть любые числа,
знаменателями же – только числа некоторого
частного вида, например,
степени десяти или шестидесяти;
Десятичные дроби в XV веке
ввел самаркандский ученый
ал — Каши.
Ничего, не зная об открытии ал – Коши,
десятичные дроби открыл второй раз,
приблизительно через 150 лет, после него,
фламандский ученый математик и инженер
Симон Стевин в труде «Децималь» (1585 г).
Отрицательные числа трактовались
так же как долг при финансовых и
бартерных расчетах.
Понятие отрицательных чисел
возникло в практике решения алгебраических уравнений.
Отрицательные числа ввели
в математический обиход
Михаэль Штифель (1487—1567)
в книге «Полная арифметика» (1544),
и Никола Шюке (1445—1500)-
его работа была обнаружена в 1848 году.
Натуральные числа
Числа,
им противоположные
1
2
3
4
6
5
-5
-4
-3
-2
-1
-6
Целые
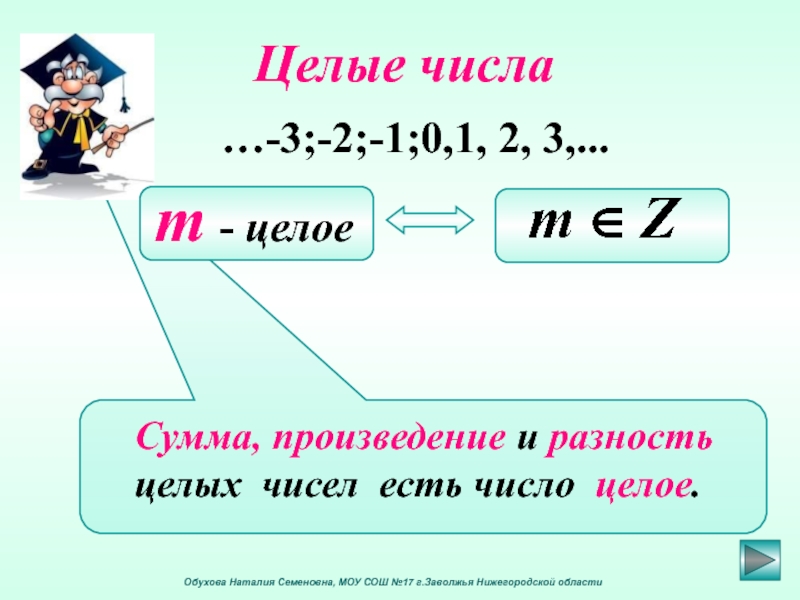
Сумма, произведение и разность
целых чисел есть число целое.
Целые числа
…-3;-2;-1;0,1, 2, 3,…
m — целое
Целые числа
Дробные числа
1
0
-4
9
10
58
7,1
3,2
0,(2)
0,1
2/7
Рациональные
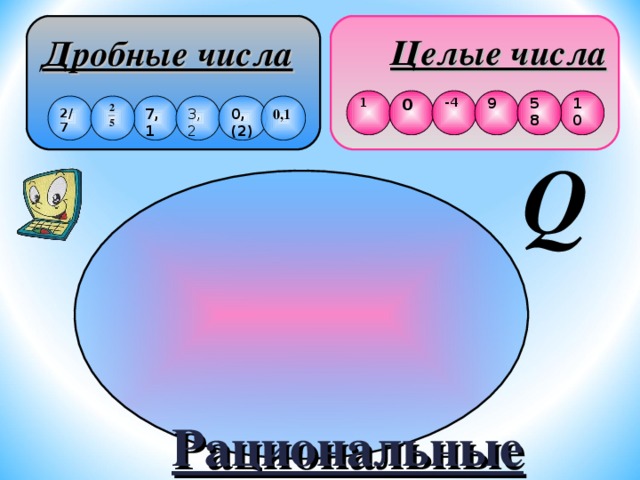
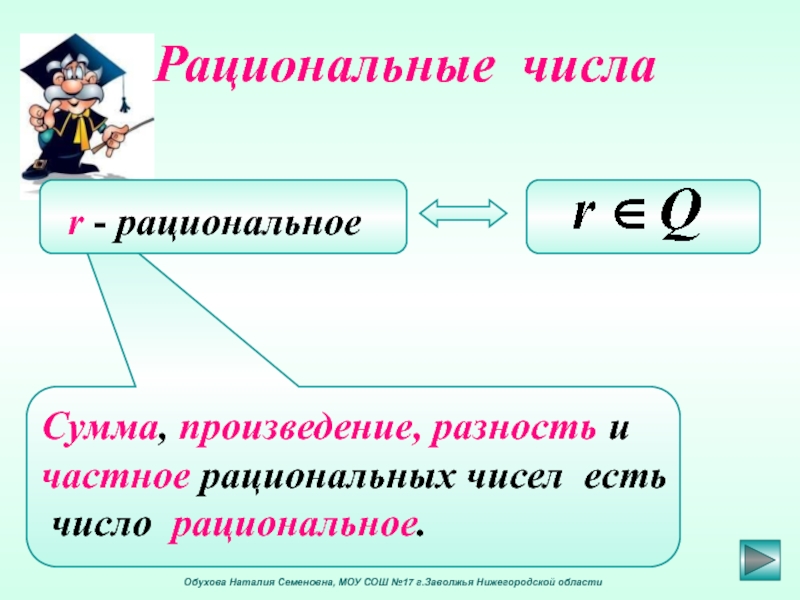
Сумма, произведение, разность и
частное рациональных чисел есть
число рациональное.
Рациональные числа
r — рациональное
Леонард Эйлер жил в России в
середине XYΙΙΙ века и внес большой вклад
в развитие математики.
Отношения между множествами натуральных,
целых и рациональных чисел наглядно демонстрирует
геометрическая иллюстрация – круги Эйлера.
Задание 1.
Вычислите значения числовых выражений и изобразите их на диаграмме Эйлера.
Вместо недостающего числа впишите букву к.
а
в
с
d
m
k
л
Выясните, какие из высказываний
истинные:
л
и
молодец
и
молодец
и
молодец
и
молодец
и
молодец
молодец
л
молодец
л
молодец
и
ошибся
и
молодец
и
ошибся
и
ошибся
ошибся
л
ошибся
л
ошибся
л
ошибся
л
ошибся
л
ошибся
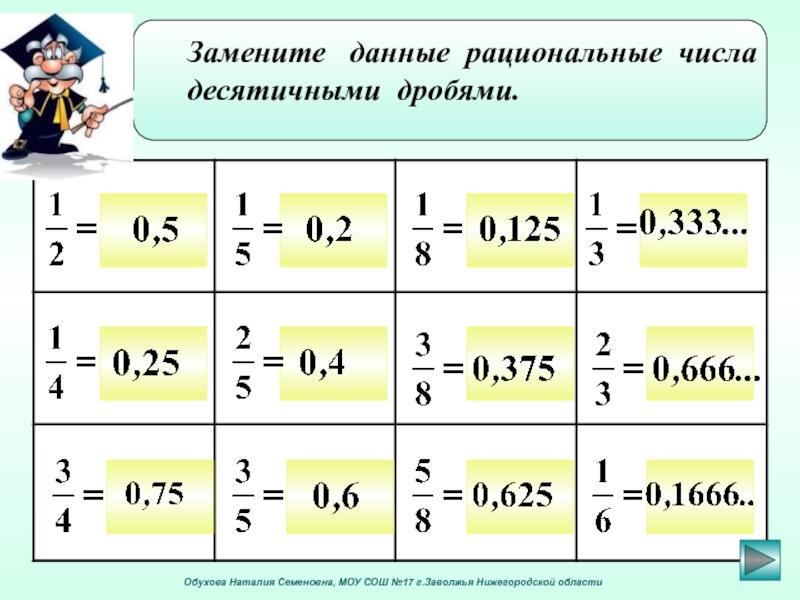
Замените данные рациональные числа
десятичными дробями.
чисто периодические
смешанные периодические
- 0,(2) 2) 2,(21) 3) 1,(1)
Прочитайте дроби:
4) -3,0(3) 5) -0,1(6) 6) 12,45(7)
Пусть х = 0,222…
10х = 2,222…
х =0,222…
10х = 2,222…
10х – х = 2,222…- 0,222
9х= 2
0,222…
Пусть х = 0,4666…
10х = 4,666…
10х =4,666…
100х = 46,666…
100х – 10х = 46,666…- 4,666
90х= 42
0,4666..
Чтобы обратить чисто периодическую дробь
в обыкновенную, нужно в числителе обыкновенной дроби поставить число,
образованное из цифр, стоящих в периоде,
а в знаменателе – написать цифру 9 столько раз,
сколько цифр в периоде.
0,(2)=
2
9
1 цифра
0,(81)=
81
2 цифры
99
Чтобы обратить смешанную периодическую дробь
в обыкновенную, нужно в числителе обыкновенной дроби
поставить число, равное разности числа, образованного цифрами, стоящими после запятой до начала второго периода, и числа, образованного из цифр, стоящих после запятой до начала первого периода;
а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, и со столькими нулями, сколько цифр между запятой и началом периода.
0,4(6)=
4
6
4
1 цифра
9
1 цифра
0
Проверь соседа
нет
да
Проверь себя
МОЛОДЦЫ !
ТВОЕ НАСТРОЕНИЕ
http://www.free-lancers.net/users/vixen/
http://www.librus.ru/childrens-corner/scientifically-cognitive-literature
/5676-mir-chisel.html
http://odur.let.rug.nl/magazijn/decennia/1745-1754_45.htm
http://project-gym6.narod.ru/1/62/euler.htm
http://sferica.by.ru/history/pi.html
http://www.peoples.ru/science/mathematics/simon_stevin/
http://www.proshkolu.ru/user/galrybo/file/455559/
Ресурсы интернета:
http://www.15a20.com.mx/images/sections/thumbs/thumb_7312558.jpg
http://gr-matem.narod.ru/
http://www.i-u.ru/biblio/archive/depman_mir/01.aspx
Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
Для счета предметов используются числа, которые называются натуральными . Для обозначения множества натуральных чисел употребляется буква N — первая буква латинского слова Naturalis — «естественный», «натуральный»
N — натуральные
1 , 2, 3, 4, 5, …
Числа,
им противоположные
Натуральные числа
5
3
6
4
2
1
-5
-4
-3
-2
-6
-1
Целые
Натуральные числа, числа им противоположные и число нуль, образуют множество целых чисел, которое обозначается Z — первой буквой немецкого слова Zahl — «число».
Z — целые
… , -3, -2, — 1 , 0,
1 , 2, 3, …
Целые числа
Дробные числа
58
10
9
-4
0
1
7,1
0,1
2/7
3,2
0,(2)
Рациональные
Множество чисел, которое можно представить в виде , называется множеством рациональных чисел и обозначается буквой Q — первой буквой французского слова Quotient — «отношение». Есть также версия, что название рациональных чисел связано с латинским словом ratio – разум.
Q — рациональные
… , -3, -2, — 1 , 0, 1, 2, 3, …
+ дроби
Отношения между множествами натуральных,
целых и рациональных чисел наглядно демонстрирует
геометрическая иллюстрация – круги Эйлера .
N Z Q
Математический символ ∈ называют знаком принадлежности ( элемент принадлежит множеству ) .
«n — натуральное число»
можно писать n ∈ N
«m — целое число»
можно писать m ∈ Z
«r — рациональное число»
можно писать r ∈ Q
Математический символ ⊂ называют знаком включения ( одно множество содержится в другом ).
«N — часть множества Z»
можно писать N ⊂ Z ,
«Z — часть множества Q»
можно писать Z ⊂ Q
Множества обозначают большими буквами,
элементы множества — маленькими буквами.
«x не принадлежит множеству X»
можно писать x ∉ X
«A не является частью (подмножеством) B»
можно писать A B .
N Z Q
Число 5 — ?
N, Z, Q
Число -7 — ?
Z, Q
Z, Q
Число -6,7 — ?
Число — ?
Q
Переведите обыкновенные дроби в десятичные:
= 0,375 – конечная десятичная дробь
Если в знаменателе стоят 2, 5, их произведение или произведение комбинацийэтих чисел – всегда КОНЕЧНАЯ ДЕСЯТИЧНАЯ ДРОБЬ!
Переведите обыкновенные дроби в десятичные:
= 0,272727272727272727… — бесконечная периодическая десятичная дробь
Для краткости написания – ПЕРИОД (круглые скобки)
0,272727272727272727…= 0,(27)
Прочитайте дроби:
- 0,(2) 2) 2,(21) 3) 1,(1)
- 0,(2) 2) 2,(21) 3) 1,(1)
4) -3,0(3) 5) -0,1(6) 6) 12,45(7)
4) -3,0(3) 5) -0,1(6) 6) 12,45(7)
чисто периодические
смешанные периодические
Любое рациональное число можно записать в виде бесконечной десятичной периодической дроби?
N Z Q
5 = 5,000… = 5,(0)
-8,37 = -8,37000… = -8,37(0)
Дроби — ?
Алгоритмы перевода рациональных чисел
в бесконечную десятичную периодическую дробь
= 0,375 = 0,375(0)
= 0,272727… = 0,(27)
Делим числитель
на знаменатель
Любое рациональное число можно записать в виде бесконечной десятичной периодической дроби?
Переведем б.п.д. дробь 0,(2)
в обыкновенную
Пусть х = 0,(2)
Это для
чисто периодической !!!
10х = 2,(2)
10х = 2,(2)
10 ( число цифр в периоде )
х = 0,(2)
10х – х = 2,(2) — 0,(2)
9х = 2
0,(2)
Переведем б.п.д. дробь 0,4(6)
в обыкновенную
Это для
смешанной периодической !!!
Пусть х = 0,4(6)
10х = 4,(6)
100х = 46,(6)
10 ( число цифр в периоде )
10х = 4,(6)
100х – 10х = 46,(6) — 4,(6)
90х = 42
0,4(6)
21
Действительные числа
Рациональные числа
Натуральные числа (N- naturalis)
- — это числа, возникающие естественным образом при счёте предметов (как в смысле перечисления, так и в смысле исчисления).
- Иногда в иностранной и переводной литературе начинают счёт с нуля. В этом случае нуль считается натуральным числом.
- В русской литературе обычно нуль исключён из числа натуральных чисел N , а множество натуральных чисел с нулём обозначается как N 0 .
Множества чисел:
- Натуральные числа, противоположные им числа и число нуль составляют множество целых чисел (Z – zahl – ( нем.) число ) .
- Кроме целых, вам известны дробные числа (положительные и отрицательные). Целые и дробные числа составляют множество рациональных чисел (Q – quotinent – (фр.) отношение ).
Математические обозначения
- ∈ — «принадлежит», символ принадлежности — ∈ (от греч. εστι — быть)
- ∪ — «объединение»,
- ∩ — «пересечение»,
- ⊂ — «содержится».
Для того чтобы записать, что какое-либо число принадлежит рассматриваемому множеству, используют знак ∈. Например, утверждение, что число 2 является натуральным (или что число 2 принадлежит множеству натуральных чисел), можно записать так: 2 ∈ N . Число –2 не является натуральным; это можно записать с помощью знака ∉: −2 ∉ N .
Математические обозначения:
Пусть каждый элемент множества B является элементом множества A . В таких случаях множество B называют подмножеством множества A .
Это записывают так: B ⊂ A (читают: B — подмножество множества A ).
Джузеппе Пеано продолжил развитие теории логики Шрёдера. Работы Шрёдера считали основополагающими для современной высшей алгебры и истории логики.
Эрнст Шрёдер (1841—1902) — немецкий математик и логик
Джузеппе Пеано (1858—1932) — итальянский математик и логик.
Запись числа
- Рациональное число записывается в виде
m/n
где m – целое число, n – натуральное.
Одно и то же рациональное число можно записать в таком виде разными способами.
- Правильной называется дробь, у которой модуль числителя меньше модуля знаменателя.
- Правильные дроби представляют рациональные числа, по модулю меньшие единицы.
- Дробь называется неправильной и представляет рациональное число, большее или равное единице по модулю.
- Неправильную дробь можно представить в виде суммы целого числа и правильной дроби, называемой смешанной дробью.
- Среди дробей, с помощью которых записывается данное рациональное число, всегда можно указать дробь с наименьшим знаменателем. Эта дробь несократима. Для целых чисел такая дробь имеет знаменатель, равный 1.
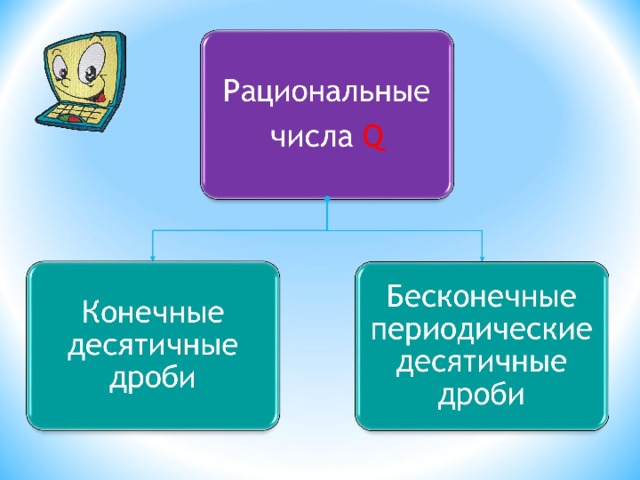
Десятичные дроби
- Конечная десятичная дробь — это дробь, знаменатель которой равен 10 n . Эта дробь записывается с помощью десятеричной позиционной системы счисления.
- Бесконечные десятичные дроби с повторяющимися группами цифр называются периодическими. Для целей сокращения повторяющаяся группа цифр (период) записывается в скобках, начиная с того места, откуда начинается повторяющаяся последовательность.
- Если период начинается сразу после запятой, то дробь называется чисто периодической . Если же период не начинается сразу после запятой, а ему предшествуют несколько цифр, то такая десятичная дробь называется смешанной периодической.
Десятичные дроби
- Период десятичной дроби — это повторяющаяся группа цифр после запятой.
- Чтобы представить обыкновенную дробь в виде десятичной , нужно числитель дроби разделить на её знаменатель.
В данной презентации присутствует как теоретический материал, так и дидактика по указанной теме.
Урок «Рациональные числа»
(8 класс)
Цели урока:
Создать условия, при которых ученик:
— расширит представления о числе, сформирует понятие «рациональное число»;
— систематизирует знания о числовых множествах;
— приобретет навыки перевода рациональных чисел в десятичную (конечную или бесконечную) дробь; бесконечных десятичных периодических дробей в рациональные числа; различные способы перевода бесконечной десятичной периодической дроби в обыкновенную дробь;
— приобретет умения работать в парах,
— разовьет навыки самостоятельной работы, умения анализировать, сравнивать, внимательно выполнять необходимые действия.
В результате ученик:
— знает, как определить вид числа, его принадлежность к числовым множествам;
— умеет правильно пользоваться математической символикой в процессе выполнения заданий;
— умеет представлять рациональное число в виде конечной или бесконечной периодической дроби;
— сможет научиться представлять бесконечную периодическую дробь в виде обыкновенной дроби;
- Организационный этап, повторение ранее изученного.
Приветствие, проверка готовности к уроку, работа в тетради – число, тема урока (слайд).
Учащиеся работают на трех уровнях сложности. Чтобы было проще организовать работу, каждый знает свой «вариант» — уровень.
Ученики получают задание на 3 варианта (от самого простого – базового, потом средний уровень и самый сложный).
как вариант: Тест проходит в режиме on-line по ссылке: http://onlinetestpad.com/ru-ru/Go/Racionalnye-chisla-8-klass-18935/Default.aspx
Я делаю тесты сама в программе INDIGO.
Учащиеся сидят по рядам в соответствии с вариантом, но у них всегда есть право выбора при проверочных работах. Такая форма рассадки хороша тем, что легко организовать работу в парах «равноценных» учеников. Ученики 1 варианта (самый легкий – базовый) работают с учителем — игра «Верю – не верю». У учащихся на бланках распечатаны вопросы. Они точно такие же, как у учителя, но напечатаны вразброс и на отдельных полосках. Задача учеников – найти тот вопрос, который сейчас задал учитель и ответить на него прямо на этом листе. Такая форма объясняется тем, что слабые ученики, как правило – это кинестетики, поэтому для них и добавляется движение во время работы. Учитель зачитывает вопросы в следующем порядке:
Верите ли вы:
- что число -5 — натуральное?
- что натуральные числа использовали для счета предметов?
- что самое маленькое натуральное число – это 0?
- что любое натуральное число (например, 4) можно записать в виде обыкновенной дроби?
- что дроби появились, когда люди стали делить между собой имущество, измерять земельные участки, исчислять время?
- что — это натуральное число?
- что любое целое число (например, -67) можно записать в виде десятичной дроби?
- что знак Î означает «принадлежит»?
- что запись «(3;5) Ì (2;9)» означает «промежуток от 3 до пяти является частью промежутка от 2 до 9»?
- что утверждение «2 Ï Z» — верное?
- что -7 > 0?
- что знак Ë означает «является частью»?
- что — это дробь?
- что дробь и рациональное число – это одно и то же?
- что множество целых чисел – самое маленькое?
Выполнение тестов заканчивается в одно время для всех учащихся (не более 10 минут с учетом орг. момента). 2 и 3 варианты не запускают проверку результатов.
2. Основной этап урока с сообщение нового блока теории и проверки имеющихся знаний.
Далее учитель рассказывает блок теории, в это время ученики должны в это время откорректировать свои ответы или убедиться в их правильности.
Блок теории – на слайдах и к ним комментарии учителя:
После этого дается время ученикам последний раз просмотреть свои ответы и проверить результаты. Для 1 варианта на слайде появляются правильные ответы. После этого еще раз вопрос: остались ли неправильные ответы и они обсуждаются вслух вместе со всеми учениками.
Следующий блок теории учащиеся фиксируют в тетрадях одновременно с объяснением учителя. Демонстрация идет на слайдах с краткими пояснениями.
3. Рефлексивно-оценочный этап
Теперь необходимо самостоятельно или с помощью соседа по парте или учителя попробовать воспроизвести алгоритмы на конкретных примерах. Работа в парах, по необходимости, с привлечением учителя. Задания для каждого варианта составлены по суммирующему принципу – чем больше решишь, тем выше отметка.
«НА 3»:
1. Определите какое множество является подмножеством множества [8;21]
а) (6;21] б) (9;20) в) [6;21] г) (6;8)
2. Для записи используется математический символ
а) ⊂ б) ∈ в) ∩ г) ∅
3. Отметьте числа -72; 6; -35,13; 106,4 на координатной оси
4. Соотнесите обыкновенные дроби с равными им десятичными.
А. Б. В. Г.
1) 0,5 2) 0,02 3) 0,12 4) 0,625
5. Сравните числа:
а) -5,7 и 0,334 б) 5,(7) и 5, 773
«НА 4»:
6. Переведите в бесконечную периодическую десятичную дробь число
8. Представьте в виде обыкновенной дроби число 1,(72)
«НА 5»:
9. Представьте в виде обыкновенной дроби число 2,9(12)
Работы сдаются учителю. Самопроверка будет осуществлена на следующем уроке после выполнения домашнего задания и повторения теории. Работа обучающего характера, поэтому важна не отметка. а понимание материала.
Подведем итог урока. Какие цели ставились в начале урока? (слайд). В тетради запишите то, в чем вы уверены, что научились делать
Давайте проговорим то, что вы написали:
— знаем, что все числа объединены во множество рациональных чисел;
— умеем пользоваться символикой и определять принадлежность чисел и промежутков;
— умеем любое число представлять в виде дроби , где или в виде бесконечной периодической дроби;
— получили возможность научиться переводить бесконечные периодические дроби в обыкновенные двумя способами, заметили, что второй способ трудно формулировать, но его применение ускорит получение результата).
4. Домашнее задание (презентация и слайды домашнего задания вывешиваются в специально для этого созданной группе в Контакте или фотографируются учащимися).
1. Дана фраза: «28 — рациональное число». Как можно записать иначе?
а) 28 ∈ N б) 28 ∈ Q в) 28 ∈ Z
2. Вычисли значение дроби − d, если a = 13; b = 36; c = 0,9; d=1,76;
3. Утверждение «−17∈(−17;5]» является: а) ложным; б) истинным
4. Выясни при каком наименьшем целом значение p число 3p+15p+2 является целым
5. Вычислить значение выражения:
Просмотр содержимого документа
«урок алгебры 8 класс «Рациональные числа» »
Слайд 1Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
Алгебра. 8
класс.
РАЦИОНАЛЬНЫЕ ЧИСЛА.
« Числа не управляют миром, но они показывают,
как управлять им».
( И. Гёте).

Слайд 2Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
(-1)7+(-1)8
Naturalis
Quotient
Ratio
Zahl
Проверка домашнего задания
Слайд 3Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
Для счета
предметов используются числа , которые называются натуральными. Для обозначения множества
натуральных чисел употребляется буква N -первая буква латинского слова Naturalis, «естественный», «натуральный»

Слайд 4Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
Тема урока:
Цель
урока:
систематизировать знания о
рациональных числах;
познакомиться с историей возникновения рациональных чисел;
выделить
общее свойство рациональных чисел.

Слайд 5Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
1

Слайд 6Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области

Слайд 7Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
Натуральные числа
1,
2, 3, 4, 5, 6…
Слайд 8Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области

Слайд 9Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
Дробные числа
Слайд 10Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
1)
доли или единичные дроби,
у которых числитель единица,
знаменателем же
может быть
любое целое число;
3)дроби общего вида, у которых числители и знаменатели могут быть любыми числами.

Слайд 11Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
Ничего, не
зная об открытии ал – Коши,
десятичные дроби открыл второй раз,
приблизительно через 150 лет, после него,
фламандский ученый математик и инженер
Симон Стевин в труде «Децималь» (1585 г).

Слайд 12Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
Отрицательные числа
трактовались
так же как долг при финансовых и
бартерных расчетах.
Понятие отрицательных чисел
возникло в практике решения алгебраических уравнений.

Слайд 13Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
Отрицательные числа
ввели
в математический обиход
Михаэль Штифель (1487—1567)
в книге «Полная арифметика»
(1544),
и Никола Шюке (1445—1500)-
его работа была обнаружена в 1848 году.

Слайд 14Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
Натуральные числа
Числа,
им
противоположные
Целые
Слайд 15Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
Целые числа
…-3;-2;-1;0,1,
2, 3,…
m — целое
Слайд 16Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
Целые числа
Дробные
числа
Рациональные

Слайд 17Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
Рациональные числа
Слайд 18Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
Леонард Эйлер
жил в России в
середине XYΙΙΙ века и внес большой
вклад
в развитие математики.
Отношения между множествами натуральных,
целых и рациональных чисел наглядно демонстрирует
геометрическая иллюстрация – круги Эйлера.

Слайд 19Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
Задание 1.
Вычислите
значения числовых выражений и изобразите их на диаграмме Эйлера.
Вместо недостающего
числа впишите букву к.
а
в
с
d
m
k

Слайд 20Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
Выясните, какие
из высказываний
истинные:
Слайд 21Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
Замените
данные рациональные числа
десятичными дробями.
Слайд 22Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
0,(2)
2) 2,(21) 3)
1,(1)
Прочитайте дроби:
4) -3,0(3) 5) -0,1(6) 6) 12,45(7)

Слайд 23Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
Пусть
х = 0,222…
10х = 2,222…
х =0,222…
10х = 2,222…
10х – х
= 2,222…- 0,222
9х= 2

Слайд 24Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
Пусть
х = 0,4666…
10х = 4,666…
10х =4,666…
100х = 46,666…
100х – 10х
= 46,666…- 4,666
90х= 42
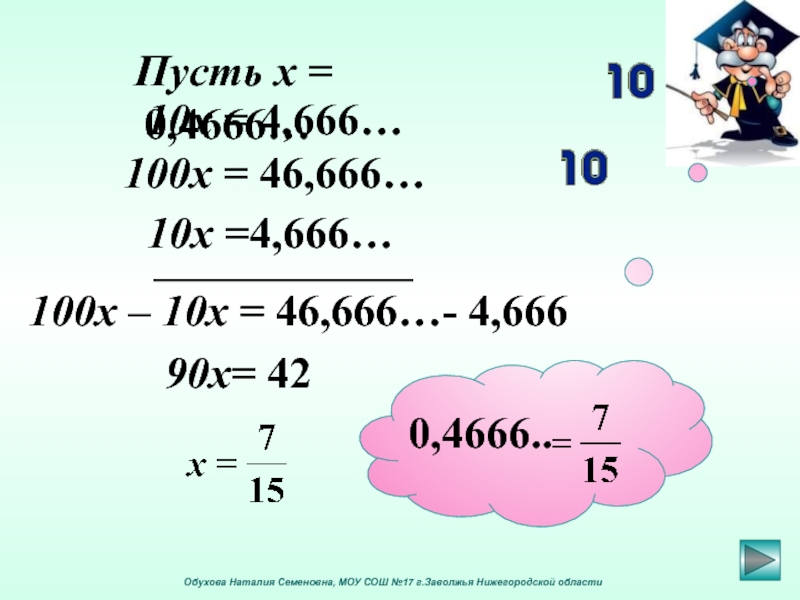
Слайд 25Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
0,(2)=
2
9
1 цифра
0,(81)=
81
2
цифры
99

Слайд 26Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
Чтобы обратить
смешанную периодическую дробь
в обыкновенную, нужно в числителе обыкновенной дроби
поставить число, равное разности числа, образованного цифрами, стоящими после запятой до начала второго периода, и числа, образованного из цифр, стоящих после запятой до начала первого периода;
а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, и со столькими нулями, сколько цифр между запятой и началом периода.
0,4(6)=
4
6
4
1 цифра
9
1 цифра
0

Слайд 27Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области

Слайд 28Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
нет
да

Слайд 29Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
ТВОЕ НАСТРОЕНИЕ

Слайд 30Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области
http://www.free-lancers.net/users/vixen/
http://www.librus.ru/childrens-corner/scientifically-cognitive-literature
/5676-mir-chisel.html
http://odur.let.rug.nl/magazijn/decennia/1745-1754_45.htm
http://project-gym6.narod.ru/1/62/euler.htm
http://sferica.by.ru/history/pi.html
http://www.peoples.ru/science/mathematics/simon_stevin/
http://www.proshkolu.ru/user/galrybo/file/455559/
Ресурсы интернета:
http://www.15a20.com.mx/images/sections/thumbs/thumb_7312558.jpg
http://gr-matem.narod.ru/
http://www.i-u.ru/biblio/archive/depman_mir/01.aspx

Слайд 3Множество натуральных чисел. (N)
3
4
1
2

Слайд 5Множество целых чисел. (Z)
0
1
2
3
4
-1
-2
-3
-4

Слайд 6Множество рациональных чисел. (Q)
0
1
2
-1
0,5
-2
-2,1
1,8
1
— _
2

Слайд 7
Целые и дробные числа образуют множество рациональных чисел.

Слайд 8Определение:
Число, которое можно записать в виде отношения ,
где а-целое число, а n-натуральное число, называют рациональным числом.
Любое целое число «а» является рациональным числом, так как его можно записать в виде а=
а
_
n
а
_
1

Слайд 9Примеры:
8
_
1
-6
_
1
0
_
1
2
_
3
—
=
-2
_
3
-4
2
_
5
=
—
22
_
_
5
=
-22
__
5
=
=
-6
8
=
0

Слайд 10Вывод:
Все числа, с которыми мы знакомы, являются рациональными

Слайд 11Из истории возникновения рациональных чисел.
В жизни, как и в сказке, люди
«открывали» рациональные числа постепенно. Вначале возникли натуральные числа. Первыми были 1 и 2. Долго не было других числительных. Вместо «3» говорили «один-два», вместо 4 «два-два».И так до шести. Потом шло «много».
С дробями люди столкнулись при разделе добычи. Для облегчения работы с дробями были придуманы десятичные дроби. В Европе их ввел в 1585 году голландский математик Симон Стевин.