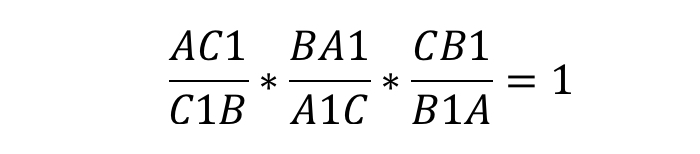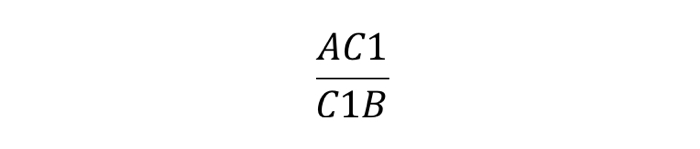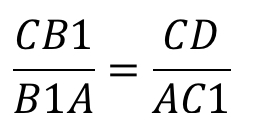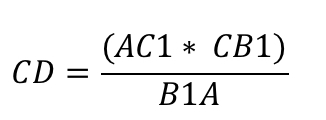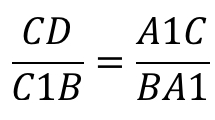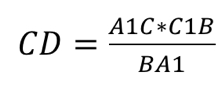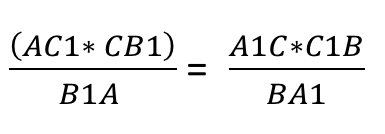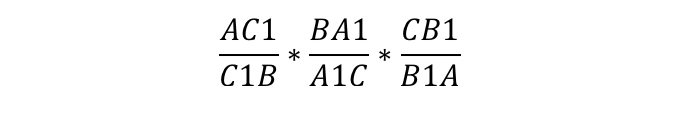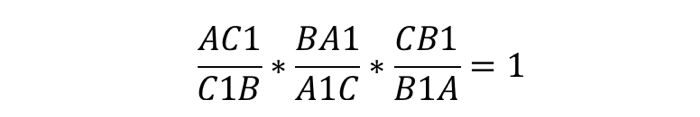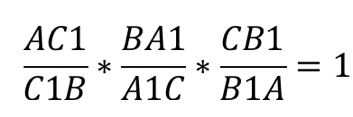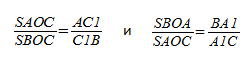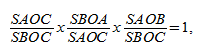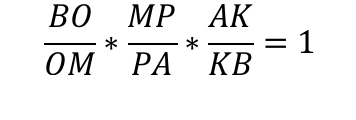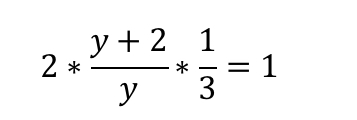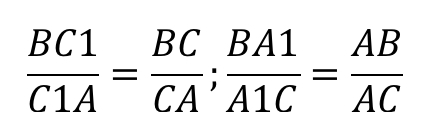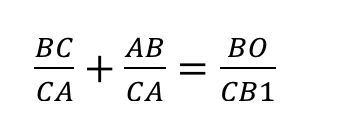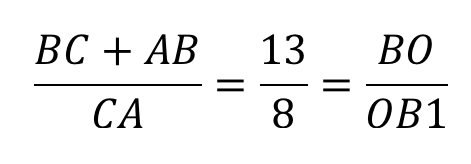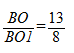������ �� ����:
������ �. �������� «������� ���� � �������»
��������� �� ���� ����:
- �����, �������, �������� �.�., ������ �� �����������, ����� 5. ������������, �������� 7. ������� �������
- �����, �������, �������� �.�., ������ �� �����������, ����� 5. ������������, �������� 8. ������� ����
��������: 1 2 3 4 5 6 7 >> [����� �����: 173]
����� M � N ����������� �������������� �� �������� AB � AC ������������ ABC, ���ޣ� AM : MB = 1 : 2, AN : NC = 3 : 2. ������ MN ���������� ����������� ������� BC � ����� F. ������� CF : BC.
����� ����� P, ������� �� ������� CC1 ������������ ABC, ��������� ������ AA1 � BB1 (����� A1 � B1 ����� �� �������� BC � CA ��������������).
��������, ��� A1B1 || AB.
������ 66969 |
���������: 3+ ������: 8,9,10,11 |
����� ����� ������ ������������ ������� ��� �������. ���������, ��� ����� ����� ��������, �� ������� ��� ��������� ������� ������������, �������� � �����-�� ������� �������������� ����������. ��������, ��� ����� ������ ���� �������� �������������� ����������.
������ 66686 |
���������: 3+ ������: 8,9,10,11 |
� ������������ $ABC$ ����� ����� $I$ ��������� ���������� $w$ ������� ������, ������������ ������� $BC$, �� ����������� � ��������� ����������� � ������ $A_B$ � $A_C$ ($A_B$ ��������� � ��� �� ������������� ������������ ������ $AI$, ��� � ����� $B$). ����� ����� ����� ����� ����������� ������ $BA_B$ � $CA_C$ � ���������� ţ ����� $A_1$. ���������� ��������� ����� $B_1$ � $C_1$. ��������, ��� ������ $AA_1$, $BB_1$, $CC_1$ ������������ � ����� �����.
������ 66813 |
���������: 3+ ������: 9,10,11 |
����� $AA_1$, $BB_1$, $CC_1$ – ������ ������������ $ABC$; $A_0$, $C_0$ – ����� ����������� ��������� ���������� ������������ $A_1BC_1$ � ������� $A_1B_1$ � $C_1B_1$ ��������������. ��������, ��� ������ $AA_0$ � $CC_0$ ������������ �� ������� ������������ $ABC$ ��� ����������� ��.
��������: 1 2 3 4 5 6 7 >> [����� �����: 173]
��������: 1 2 3 4 >> [����� �����: 16]
���������� S �������� ����������� S1 � S2 � ������ A1 � A2.
��������, ��� ������ A1A2 �������� ����� ����� ����������� ����� ������� ��� ����� ���������� ����������� � ����������� S1 � S2.
������ 56898 |
���������: 5 ������: 9 |
�� �������� BC, CA � AB ������������ ABC (���
�� �� ������������) ����� ����� A1, B1 � C1 ��������������.
��������, ��� ����� A1, B1 � C1 ����� �� ����� ������ ����� �
������ �����, �����
.
.
= 1 (������� �������).
������ 56899 |
���������: 5 ������: 9 |
�) � ������������ ABC ��������� ����������� ������� ����� AA1, BB1 �
CC1 (����� A1, B1 � C1 ����� �� ������ BC, CA � AB).
��������, ��� ����� A1, B1 � C1 ����� �� ����� ������.
�) � ������������ ABC ��������� ����������� AA1 � BB1 � �����������
�������� ���� CC1. ��������, ��� ����� A1, B1 � C1 ����� �� �����
������.
������ 56900 |
���������: 5 ������: 9 |
����������� � ��������� ���������� ����������������� ������������ ABC � ������ A, B � C
���������� ����������� ������ � ������ A1, B1 � C1. ��������, ���
����� A1, B1 � C1 ����� �� ����� ������.=-1
������ 56901 |
���������: 5 ������: 9 |
������ ������ 5.85, �) � ������� ������� �������.
��������: 1 2 3 4 >> [����� �����: 16]
Всего: 47 1–20 | 21–40 | 41–47
Добавить в вариант
Каждое из ребер треугольной пирамиды ABCD имеет длину 1. Точка P на ребре AB, точка Q на ребре BC, точка R на ребре CD взяты так, что Плоскость PQR пересекает прямую AD в точке S. Найти величину угла между прямыми SP и SQ.
Источник: А. Ларин: Тренировочный вариант № 42.
Объем пирамиды ABCD равен 5. Через середины ребер AD и BC проведена плоскость, пересекающая ребро CD в точке M. При этом DM : MC = 2 : 3. Найти площадь сечения, если расстояние от плоскости сечения до вершины A равно 1.
Источник: А. Ларин: Тренировочный вариант № 54.
На сторонах AB, BC и CA треугольника ABC отложены соответственно отрезки
а) Докажите, что где
б) Найдите, какую часть от площади треугольника ABC составляет площадь треугольника MNK.
Источник: А. Ларин: Тренировочный вариант № 67.
В правильной четырехугольной пирамиде SABCD с вершиной S, точка M — середина ребра BS. Найдите площадь сечения, проведенного через прямую AM параллельно одной из диагоналей основания, указанная диагональ не принадлежит сечению. Стороны основания пирамиды равны а высота пирамиды равна 9.
Источник: А. Ларин: Тренировочный вариант № 19.
В треугольной пирамиде SABC на ребре SB взята точка M, делящая отрезок SB в отношении 3 : 5, считая от вершины S. Через точки A и M параллельно медиане BD треугольника ABC проведена плоскость. В каком отношении эта плоскость делит объем пирамиды?
Источник: А. Ларин: Тренировочный вариант № 27.
В треугольнике ABC на стороне AB расположена точка K так, что AK : KB = 3 : 5. На прямой AC взята точка E так, что AE = 2CE. Известно, что прямые BE и CK пересекаются в точке O. Найдите площадь треугольника ABC, если площадь треугольника BOC равна 20.
Источник: А. Ларин: Тренировочный вариант № 36.
Плоскость пересекает боковые ребра SA и SB треугольной пирамиды SABC в точках K и L соответственно и делит объем пирамиды пополам
а) Постройте сечение пирамиды плоскостью, если SK : SA = 2 : 3, SL : SB = 4 : 5.
б) В каком отношении эта плоскость делит медиану SN грани SBC?
Источник: А. Ларин: Тренировочный вариант № 93.
Сторона основания правильной четырехугольной пирамиды SABCD равна 6, а высота 4. Точки K, P, M — середины ребер AB, BC, SD.
а) Постройте сечение пирамиды плоскостью, проходящей через точки K, M, P.
б) Найдите площадь этого сечения.
Источник: А. Ларин: Тренировочный вариант № 102.
В правильной треугольной пирамиде SABC точка М — середина ребра SC, точка K — середина ребра AB.
а) Докажите, что прямая MK делит высоту SH пирамиды в отношении 1 : 3.
б) Найдите угол между прямой MK и плоскостью ABC, если известно, что AB = 6, SA = 5.
Источник: А. Ларин: Тренировочный вариант № 121.
В правильной четырехугольной пирамиде PABCD все ребра равны между собой. На ребре PC отмечена точка K.
а) Докажите, что сечение пирамиды плоскостью ABK является трапецией.
б) Найдите угол, который образует плоскость ABK с плоскостью основания пирамиды, если известно, что PK : KC = 3 : 1.
Источник: А. Ларин: Тренировочный вариант № 128.
Даны треугольники ABC и A1B1C1. Прямые AA1, BB1, CC1 пересекаются в одной точке. Прямые AB и A1B1 пересекаются в точке C2. Прямые АС и A1C1 пересекаются в точке B2. Прямые BC и B1C1 пересекаются в точке A2.
а) Докажите, что точки A2, B2, C2 лежат на одной прямой.
б) Найдите отношение площади треугольника A1B1C1 и площади треугольника ABC, если высоты треугольника ABC равны а высоты треугольника A1B1C1 равны
Источник: А. Ларин: Тренировочный вариант № 134.
В правильной треугольной пирамиде PABC к основанию ABC проведена высота РО. Точка K — середина СО.
а) Докажите, что плоскость, проходящая через точки А, P и K делит ребро BC в отношении 1:4.
б) Найдите объем большей части пирамиды PABC, на которые ее делит плоскость APK, если известно, что
Источник: А. Ларин: Тренировочный вариант № 145.
Дана правильная шестиугольная пирамида SABCDEF с вершиной S.
а) Докажите, что плоскость, проходящая через середины рёбер SA и SD и вершину C, делит апофему грани ASB в отношении 2 : 1, считая от вершины S.
б) Найдите отношение, в котором плоскость, проходящая через середины рёбер SA и SD и вершину C, делит ребро SF, считая от вершины S.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016
На отрезке BD взята точка C. Биссектриса BL равнобедренного треугольника ABC с основанием BC является боковой стороной равнобедренного треугольника BLD с основанием BD.
а) Докажите, что треугольник DCL равнобедренный.
б) Известно, что В каком отношении прямая DL делит сторону AB?
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016
В правильной шестиугольной пирамиде SABCDEF с вершиной S боковое ребро вдвое больше стороны основания.
а) Докажите, что плоскость, проходящая через середины рёбер SA и SE и вершину C, делит ребро SB в отношении 3 : 1, считая от вершины S.
б) Найдите отношение, в котором плоскость, проходящая через середины рёбер SA и SE и вершину C, делит ребро SF, считая от вершины S.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016
На сторонах AD и BC параллелограмма AВCD взяты соответственно точки M и N, причем ВN : NC = 1 : 3. Оказалось, что прямые AN и АС разделили отрезок BM на три равные части.
а) Докажите, что точка M — середина стороны АD параллелограмма.
б) Найдите площадь параллелограмма ABCD, если известно, что площадь четырехугольника, ограниченного прямыми АN, AС, BM и BD равна 16.
Источник: А. Ларин: Тренировочный вариант № 152.
В прямоугольном треугольнике АВС с прямым углом С точки М и N — середины катетов АС и ВС соответственно, СН — высота.
а) Докажите, что прямые МН и NH перпендикулярны.
б) Пусть Р — точка пересечения прямых АС и NH, а Q — точка пересечения прямых BC и МН. Найдите площадь треугольника PQM, если АН = 12 и ВН = 3.
Источник: ЕГЭ по математике 06.06.2016. Основная волна. Вариант 601 (C часть).
В прямоугольном треугольнике АВС с прямым углом С точки М и N — середины катетов АС и ВС соответственно, СН — высота.
а) Докажите, что прямые МН и NH перпендикулярны.
б) Пусть Р — точка пересечения прямых АС и NH, а Q — точка пересечения прямых BC и МН. Найдите площадь треугольника PQM, если АН = 4 и ВН = 2.
Источники:
Задания 16 (С4) ЕГЭ 2016;
ЕГЭ по математике 06.06.2016. Основная волна. Вариант 605 (C часть). .
На отрезке BD взята точка C. Биссектриса BL равнобедренного треугольника ABC с основанием BC является боковой стороной равнобедренного треугольника BLD с основанием BD.
а) Докажите, что треугольник DCL равнобедренный.
б) Известно, что В каком отношении прямая DL делит сторону AB?
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016
На диагонали AC параллелограмма АВСD отмечены точки Е и Р, причем АЕ : ЕР : РС = 1 : 2 : 1. Прямые DЕ и DР пересекают стороны АВ и ВС в точках К и М соответственно.
А) Докажите, что КМ параллельна АС.
Б) Найдите площадь параллелограмма АВСD, если известно, что площадь пятиугольника ВКЕРМ равна 30.
Источник: А. Ларин: Тренировочный вариант № 171.
Всего: 47 1–20 | 21–40 | 41–47
§2. Задачи о делении отрезка. Теорема Менелая
Задача о «делении отрезка», как правило, решаются дополнительным построением – проведением прямой, параллельной рассекающей, и использованием подобия или теоремы о пересечении сторон угла параллельными прямыми. Общий подход к решению таких задач даёт теорема Менелая (далее напомним формулировку и доказательство, в задании 9-го класса это уже было сделано).
Точка $$ D$$ лежит на стороне $$ BC$$, точка $$ K$$ — на стороне $$ AB$$ треугольника $$ ABC$$, прямые $$ AD$$ и $$ CK$$ пересекаются в точке $$ O$$ (рис. 15). Найти отношение $$ AO:OD$$, если $$ AK:KB=1:3$$ и $$ BD:DC=2:3$$.
 |
| Рис. 15 |
Расставим на рисунке данные о делении сторон. Чтобы решение стало более понятным, сделаем ещё один рисунок (рис. 15а), на нём проведём $$ DSleft|right|CK$$.
Рассматриваем треугольник $$ KBC$$. Из `DS«||«CK`$$ $$по утверждению $$ 2°$$
(второй признак подобия треугольников) следует $$ KS:KB=CD:CB$$, откуда $$ KS={displaystyle frac{3}{5}}·3x={displaystyle frac{9}{5}}x$$. (Ставим это на рисунке). На этом этапе удобно сделать ещё один рисунок (рис. 15б), либо на рисунке 15а провести прямую `AD` и отметить точку $$ O$$.
В треугольнике $$ ASD$$ по построению $$ SDleft|right|KO$$, По утверждению $$ 2°$$ имеем $$ AO:OD=AK:KS$$, откуда следует $$ AO:OD=5:9$$
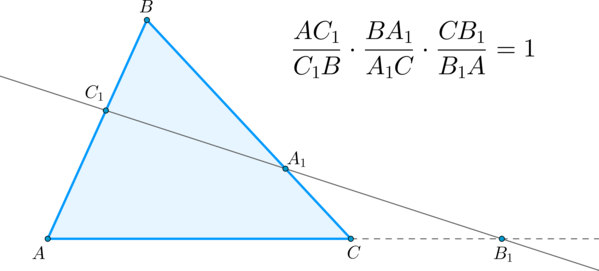
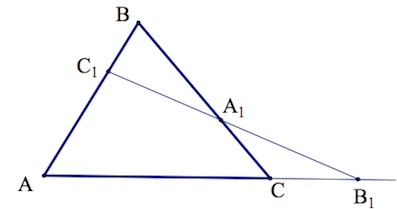
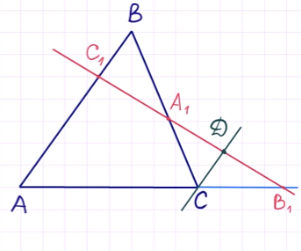
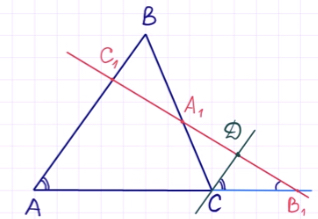
Точки `A_1` и `C_1`, расположенные на сторонах `BC` и `AB` треугольника `ABC`, и точка `B_1`, расположенная на продолжении стороны `AC` за точку `C`, лежат на одной прямой тогда и только тогда, когда имеет место равенство:
$$ {displaystyle frac{A{C}_{1}}{{C}_{1}B}}·{displaystyle frac{B{A}_{1}}{{A}_{1}C}}·{displaystyle frac{C{B}_{1}}{{B}_{1}A}}=1$$. (`**`)
1. Пусть точки $$ {B}_{1},{A}_{1},{C}_{1}$$ лежат на одной прямой.
Проводим $$ CKleft|right|AB$$ (рис. 16а):
$$begin{array}{l}left.triangle A_1CKsimtriangle A_1BC_1right|Rightarrowdfrac{CK}{C_1B}=dfrac{A_1C}{BA_1};\left.triangle B_1AC_1simtriangle B_1CKright|Rightarrowdfrac{AC_1}{CK}=dfrac{B_1A}{B_1C}.end{array}$$
Почленно перемножив, получим
$$ {displaystyle frac{A{C}_{1}}{{C}_{1}B}}={displaystyle frac{{A}_{1}C}{B{A}_{1}}}·{displaystyle frac{{B}_{1}A}{C{B}_{1}}}$$,
откуда и следует
$$ {displaystyle frac{A{C}_{1}}{{C}_{1}B}}·{displaystyle frac{B{A}_{1}}{{A}_{1}C}}·{displaystyle frac{C{B}_{1}}{{B}_{1}A}}=1$$
(стрелочки на рис. 16а показывают последовательность взятия отрезков, движение начинается в точке `A` и в ней же заканчивается).
2. Пусть имеет место равенство (`**`). Через две точки $$ {B}_{1}$$ и $$ {A}_{1}$$ проводим прямую, точку пересечения с отрезком $$ AB$$ обозначаем $$ {C}_{2}$$ (рис. 16б). Точки $$ {A}_{1},{B}_{1}$$ и $$ {C}_{2}$$ лежат на одной прямой, по доказанному имеет место
$$ {displaystyle frac{A{C}_{1}}{{C}_{1}B}}·{displaystyle frac{B{A}_{1}}{{A}_{1}C}}·{displaystyle frac{C{B}_{1}}{{B}_{1}A}}=1.$$
Сравнивая с равенством (`**`), устанавливаем, что $$ {displaystyle frac{A{C}_{2}}{{C}_{2}B}}={displaystyle frac{A{C}_{1}}{{C}_{1}B}}$$ и показываем, что точки $$ {C}_{2}$$ и $$ {C}_{1}$$ совпадают, т. к. делят отрезок $$ AB$$ на равные отрезки.
Применим теорему Менелая к решению примера 7 (см. рис. 15): рассматриваем треугольник $$ BAD$$ и секущую $$ CK$$ (она определяет три точки: $$ K,O,C$$ ). Имеем: $$ {displaystyle frac{BK}{KA}}·{displaystyle frac{AO}{OD}}·{displaystyle frac{DC}{CB}}=1$$,
т. е. $$ {displaystyle frac{3x}{x}}·{displaystyle frac{AO}{OD}}·{displaystyle frac{3y}{5y}}=1$$ откуда $$ {displaystyle frac{AO}{OD}}={displaystyle frac{5}{9}}$$.
Если при тех же условиях задачи 7 требуется определить, какую часть площади треугольника составляет, например, площадь четырёхугольника $$ KODB$$ то полезно сначала решить задачу о «делении отрезка» и найти, например, $$ AO:OD=5:9$$, а затем использовать тот факт, что площади треугольников с одинаковыми высотами относятся как длины их оснований:
$$ {S}_{ABC}=S; {S}_{ADC}={displaystyle frac{3}{5}}S$$ $$ ($$ т. к. $$ DC={displaystyle frac{3}{5}}BC$$$$ )$$;
$$ {S}_{OCD}={displaystyle frac{9}{14}}{S}_{ADC}={displaystyle frac{9}{14}}left({displaystyle frac{3}{5}}Sright)={displaystyle frac{27}{70}}S$$ $$ ($$ т. к. $$ OD={displaystyle frac{9}{14}}AD$$$$ )$$;
$$ {S}_{KCB}={displaystyle frac{3}{4}}S$$ $$ ($$ т. к. $$ BK={displaystyle frac{3}{4}}AB$$$$ )$$, поэтому
$$ {S}_{KODB}={S}_{KCB}-{S}_{OCD}={displaystyle frac{3}{4}}S-{displaystyle frac{27}{70}}S={displaystyle frac{51}{140}}S$$.
16. Задачи по планиметрии
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на теоремы Менелая, Чевы и Стюарта
(blacktriangleright) Теорема Менелая: пусть прямая пересекает треугольник в точке (C_1) на стороне (AB), в точке (A_1) на стороне (BC) и в точке (B_1) на продолжении стороны (AC). Тогда имеет место следующее соотношение:
(blacktriangleright) Теорема, обратная теореме Менелая: пусть в треугольнике точка (B_1) лежит на продолжении стороны (AC), а точки (A_1, C_1) — на сторонах (BC) и (AB) соответственно. Тогда, если выполнено равенство [dfrac{AB_1}{B_1C}cdot dfrac{CA_1}{A_1B}cdot dfrac{BC_1}{C_1A}=1,] то точки (A_1, B_1, C_1) лежат на одной прямой.
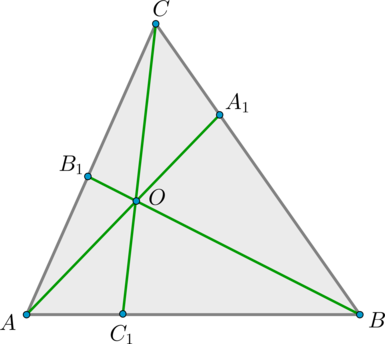
Теорема Чевы: пусть на сторонах треугольника (ABC) выбраны точки (A_1in BC, B_1in AC, C_1in AB). Отрезки (AA_1, BB_1, CC_1) пересекаются в одной точке тогда и только тогда, когда выполнено равенство [{large{dfrac{AB_1}{B_1C}cdot dfrac{CA_1}{A_1B}cdot
dfrac{BC_1}{C_1A}=1}}]
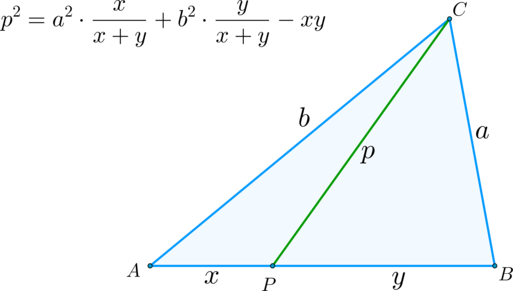
(blacktriangleright) Теорема Стюарта: пусть в треугольнике на стороне (AB) отмечена точка (P). Тогда, если (CP=p, AP=x,
BP=y,AC=b, BC=a), верно следующее соотношение:
(blacktriangleright) С помощью теоремы Стюарта выводятся формулы нахождения биссектрис и медиан треугольника:
I. Если (l_c) — биссектриса, проведенная к стороне (c) и разбивающая эту сторону на отрезки (x) и (y), а (a,b) — две другие его стороны, то [{large{l^2_c=ab-xy}}]
II. Если (m_c) — медиана, проведенная к стороне (c) треугольника, а (a,b) — две другие его стороны, то [{large{m^2_c=dfrac{2a^2+2b^2-c^2}4}}]
Задание
1
#2826
Уровень задания: Легче ЕГЭ
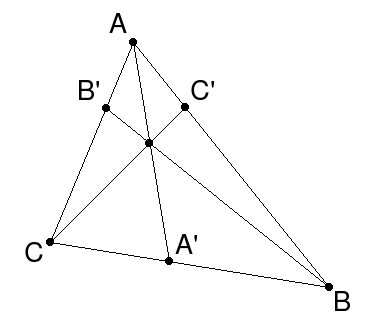
Докажите, что биссектрисы треугольника пересекаются в одной точке.
Пусть нам дан (triangle ABC), проведем в нем биссектрисы (AA_1,
BB_1, CC_1) и докажем что они пересекаются в одной точке.
Воспользуемся свойством биссектрисы для всех трех биссектрис:
Для биссектрисы (AA_1: dfrac{BA_1}{A_1C} =dfrac{AB}{AC})
Для биссектрисы (BB_1: dfrac{CB_1}{B_1A} =dfrac{BC}{BA})
Для биссектрисы (CC_1: dfrac{AC_1}{C_1B} =dfrac{CA}{CB})
Воспользуемся теоремой Чевы: [dfrac{BA_1}{A_1C} cdot dfrac{CB_1}{B_1A} cdot
dfrac{AC_1}{C_1B} = dfrac{AB}{AC} cdot dfrac{BC}{BA} cdot
dfrac{CA}{CB} = dfrac{ABcdot BC cdot CA}{ABcdot BC cdot CA} =1.]
Следовательно, биссектрисы треугольника пересекаются в одной точке.
Ответ:
Доказательство
Задание
2
#2827
Уровень задания: Легче ЕГЭ
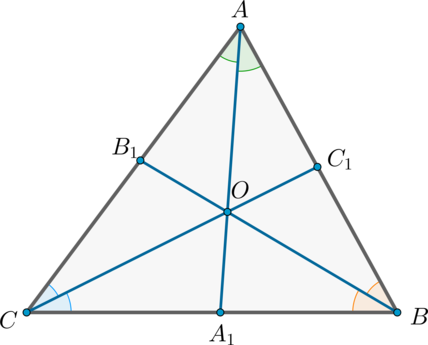
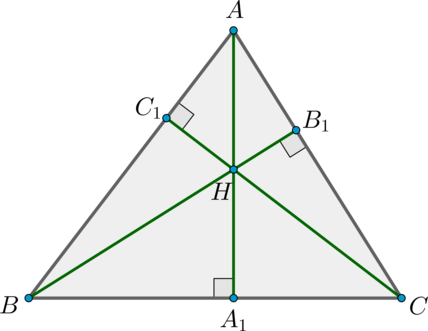
Докажите, что высоты треугольника пересекаются в одной точке.
Пусть нам дан (triangle ABC), проведем в нем высоты (AA_1,
BB_1, CC_1) и докажем что они пересекаются в одной точке.
Заметим, что: [begin{aligned}
&BA_1= cos{angle B} cdot AB,qquad
A_1C= cos{angle C} cdot AC,\
&CB_1= cos{angle C} cdot BC,qquad
B_1A= cos{angle A} cdot AB,\
&AC_1= cos{angle A} cdot AC,qquad
C_1B= cos{angle B} cdot BC.
end{aligned}] Воспользуемся теоремой Чевы: [begin{aligned}
&dfrac{BA_1}{A_1C} cdot dfrac{CB_1}{B_1A} cdot
dfrac{AC_1}{C_1B} = dfrac{cos{angle B} cdot AB}{cos{angle C}
cdot AC} cdot dfrac{cos{angle C} cdot BC}{cos{angle A}
cdot AB} cdot dfrac{cos{angle A} cdot AC}{cos{angle B}
cdot BC} =\[1.5ex]
= & dfrac{ABcdot BC cdot CA cdot cos{angle A} cdot cos{angle B} cdot cos{angle C}}{ABcdot BC cdot CA cdot cos{angle A} cdot cos{angle B} cdot cos{angle C}} =1,.
end{aligned}]
Следовательно, высоты треугольника пересекаются в одной точке.
Ответ:
Доказательство
Задание
3
#2828
Уровень задания: Легче ЕГЭ
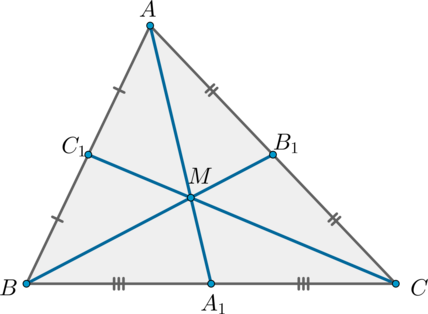
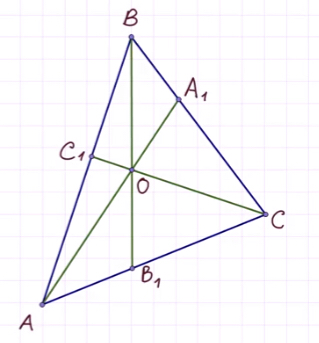
Докажите, что медианы треугольника пересекаются в одной точке.
Пусть нам дан (triangle ABC), проведем в нем медианы (AA_1, BB_1,
CC_1) и докажем что они пересекаются в одной точке.
Воспользуемся теоремой Чевы: [dfrac{AB_1}{B_1C} cdot
dfrac{CA_1}{A_1B} cdot dfrac{BC_1}{C_1A} =dfrac{1}{1} cdot
dfrac{1}{1} cdot dfrac{1}{1} =1,] так как (A_1, B_1, C_1) – середины сторон (BC, AC, AB) соответственно.
Следовательно, медианы треугольника пересекаются в одной точке.
Ответ:
Доказательство

Вся теория по №18 за 3 часа. ЕГЭ 2023 по профильной математике
Вся теория по №18 за 3 часа. ЕГЭ 2023 по профильной математике
Теоремы Чевы и Менелая – одни из базовых основ планиметрии и геометрии, которым репетиторы и школьные учителя уделяют особое внимание, а ученикам задают писать научные доклады и рефераты на эту тему в качестве домашнего задания.
Их изучение рекомендуется не только в том случае, если вы – математик, но и в помощь ученикам старшего уровня (по уровню сложности может подойти и любой средний класс) и студентам профильных специальностей, которые всерьёз интересуются данной наукой.
Именно для этого мы подготовили данный материал. В нем вы узнаете, чем интересны данные основы, принципы их доказательств и рассмотрите решения некоторых задач из ЕГЭ.
Формулировка теоремы Менелая
Менелай Александрийский — древнегреческий математик и астроном, живший в I в. Большой вклад внес в развитие сферической тригонометрии, где для получения формул использовал именно эту теорему, которую теперь изучают все школьники.
Прежде чем приступить к проработке, сделаем соответствующий рисунок.
Что мы имеем? Треугольник ABC и прямую, которая пересекает две его стороны и продолжение третьей стороны.
Особенность теоремы заключается и в том, что приведённый рисунок чаще всего встречается в заданиях формата ЕГЭ. Это – весьма распространённая геометрическая конструкция, когда какая-то прямая таким образом пересекает треугольник.
Если мы видим приведённый выше рисунок, можно записать формулу:
Запомнить отношение просто: действуем по принципу «вершина — точка, точка — вершина». То есть, если на стороне AB нам дана некоторая точка C1, их отношенное записывается следующим образом:
Доказательство теоремы
Для доказательства теоремы Менелая проведём через точку C прямую, параллельную AB, таким образом:
Обозначим точку пересечения данной прямой с B1C1
через точку D.
В таком случае мы получим несколько пар подобных треугольников.
Сторона CD параллельна AB. Тогда первой парой подобных треугольников будут треугольники B1CD и B1AC1. Они подобны по второму признаку подобия треугольников, то есть по двум пропорциональным сторонам и углу B1 между ними.
Углы B1CD и B1AC1 равны как соответственные при параллельных прямых CD, AB и секущей AC.
Анализируя данную пару подобных треугольников, можно записать условие пропорциональности сходственных сторон, а именно:
Так как сторона CD не является составляющей исходного равенства, для дальнейшего доказательства её нужно выразить.
Используя описанное равенства, применив свойства пропорции, запишем:
Запишем следующую пару подобных треугольников: треугольники CDA1 и BC1A1 подобны, так как углы CA1D и BA1C1 равны как вертикальные. Кроме этого, угол CDA1 равен углу BC1A1, как накрест лежащие при параллельных прямых CD, AB и секущей C1D.
Покажем это на рисунке:
Из данного подобия можно записать некоторую пропорциональность сходственных сторон:
Так же выразим CD:
Осталось лишь приравнять. Дроби, с помощью которых мы выразили CD – равны.
Таким образом получаем:
Умножив обе дроби на часть, обратную левой дроби, мы получили исходное равенство:
Что и требовалось доказать.
Формулировка теоремы Чевы
Джованни Чева — итальянский математик, инженер. Годы жизни 1648 — 1734 гг. Основные труды ученого в области геометрии и механики.
Рассматриваемая теорема была доказана ученым в 1678 г.
Рассмотрим приведённый ниже рисунок:
Теорема звучит так: любые произвольные отрезки, выходящие из вершин треугольника, (но с одним условием: они должны пересекаться в одной точке) делят противолежащие этим вершинам стороны таким образом, что истинно равенство:
В честь ученого, доказавшего эту теорему, данные отрезки называют «чевианами».
Доказательство теоремы
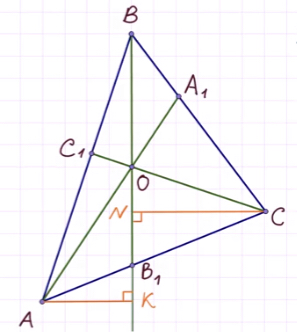
Рассмотрим рисунок:
Итак, мы имеем треугольник ABC и произвольные чевианы AA1 и BB1.
Третья чевиана CC1 обязательно должна проходить через точку пересечения первых двух. При этом получается, что:
Обозначим за O точку пересечения данных прямых.
Продлим медиану BB1.
Проведём перпендикуляры из вершин A и С таким образом:
Запишем соотношение:
Треугольники AKB1 и CNB1
подобны по острому углу.
Аналогично получаем:
Теперь перемножим равенства:
что и требовалось доказать.
Применение теорем Чевы и Менелая при решении задач ЕГЭ
Теорема Менелая (как и обратная) применима и в первой части экзаменационного бланка, и в 16-м задании. Рассмотрим пару таких задач.
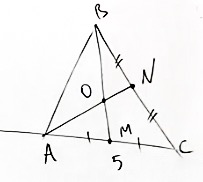
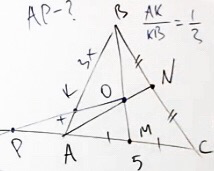
Задача 1
Дан треугольник ABC (см. рисунок ниже) с продолжением стороны CA. Также проведены медианы BM и AN. Точку их пересечения обозначим за O.
Возьмём точку K на стороне AB, такую, что AK относится к AB, как 1/3.
AC = 4 см, AM = 2 см.
Проведём прямую OK до пересечения со стороной AC. Точку их пересечения обозначим за P.
Сторону AP обозначим за y.
Найти: чему равен отрезок AP.
Решение:
Так как отношение сторон AB и AK равно 1/3, следовательно, AK = x, а KB = 3x.
Рассмотрим треугольник ABM. Для него берём прямую OP.
Таким образом мы нашли искомые точки P, A, M, O, K и B.
Запишем теорему Менелая к данному рисунку.
Подставляем в это соотношение известные данные:
В итоге мы получаем, что y = 4.
Ответ: отрезок AP = 4 см.
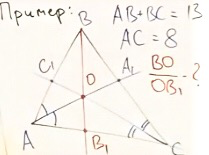
Задача 2
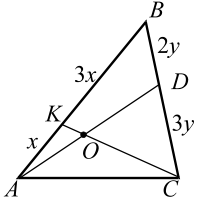
Задача, связанная со свойствами теоремы Чевы.
Рассмотрим рисунок:
Дано:
-
сумма AB и BC равна 13;
-
AC = 8 см.
Найти: отношение BO и OB1.
Итак, запишем отношение:
Подставляем:
Конечным результатом является дробь 13/8.
Ответ: