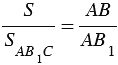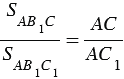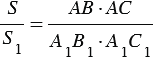Теорема о площади треугольника
Площадь треугольника равна половине произведения его сторон на синус угла между ними.
Доказательство:
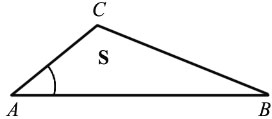
Рассмотрим произвольный треугольник ABC. Пусть в нем сторона BC = a, сторона CA = b и S – площадь этого треугольника. Необходимо доказать, что S = (1/2)*a*b*sin(C).
Для начала введем прямоугольную систему координат и поместим начало координат в точку С. Расположим нашу систему координат так, чтобы точка B лежала на положительном направлении оси Сх, а точка А имела бы положительную ординату.
Если все выполнить правильно, то должен получится следующий рисунок.
Площадь данного треугольника можно вычислить по следующей формуле: S = (1/2)*a*h, где h — это высота треугольника. В нашем случае высота треугольника h равна ординате точки А, то есть h = b*sin(C).
Учитывая полученные результат, формулу площади треугольника можно переписать следующим образом: S = (1/2)*a*b*sin(C). Что и требовалось доказать.
Решение задач
Задача 1. Найти площадь треугольника ABC, если а) AB = 6*√8 см, АС = 4 см, угол А = 60 градусов б) BC = 3 см, AB = 18*√2 см, угол B= 45 градусов в) AC = 14 см, CB = 7 см, угол C= 48 градусов.
Решение:
По доказанной выше теореме площадь S треугольника ABC равна:
S = (1/2)*AB*AC*sin(A).
Произведем вычисления.:
а) S = ((1/2) *6*√8*4*sin(60˚)) = 12*√6 см^2.
б) S = (1/2)*BC*BA*sin(B)=((1/2)* 3*18*√2 *(√2/2)) = 27 см^2.
в) S = (1/2)*CA*CB*sin(C) = ½*14*7*sin48˚ см^2.
Значение синуса угла считаем на калькуляторе либо используем значения из таблицы значений тригонометрических углов. Ответ:
а) 12*√6 см^2.
б) 27 см^2.
в) приблизительно 36.41 см^2.
Задача 2. Площадь треугольника ABC равна 60 см^2. Найдите сторону AB, если AC = 15 см, угол А = 30˚.
Решение:
Положим S – площадь треугольника ABC. По теореме о площади треугольника имеем:
S = (1/2)*AB*AC*sin(A).
Подставим в неё имеющиеся у нас значения:
60 = (1/2)*AB*15*sin30˚ = (1/2)*15*(1/2)*AB=(15/4)*AB.
Отсюда выражаем длину стороны AB: AB = (60*4)/15 = 16.
Ответ: 16 см.
Нужна помощь в учебе?
Предыдущая тема: Формулы для вычисления координат точки: алгоритмы и задачи
Следующая тема: Теорема синусов: доказательство и задача для примера
| Нравится | Нравится |
Теорема
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
(S=frac12abcdotsin C)
Вывод формулы с доказательством
Для доказательства теоремы возьмем произвольный треугольник ABC.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Пусть BC = a, CA = b, S — площадь треугольника ABC.
Докажем, что (S=frac12abcdotsin C)
Введем координатную плоскость и впишем в нее треугольник ABC так, чтобы:
- точка C совпадала с началом координат;
- точка B лежала на положительной оси Cx;
- точка A находилась в верхней полуплоскости.
С учетом описанных условий вычисление площади треугольника можно произвести по формуле:
(S=frac12ah)
где h — высота треугольника. В данном случае h равна ординате точки A.
Получается, что (h=bcdotsin C.)
Это связано с тем, что (sin C) равен отношению противолежащего катета (то есть h) к гипотенузе (то есть к b):
(sin C=frac hb)
Отсюда выражаем h и получаем:
(h=bcdotsin C)
Как следствие (S=frac12abcdotsin C), то есть вместо (h) подставляем (bcdotsin C). Теорема геометрии доказана.
Пример решения задачи
Задача
Дан прямоугольный треугольник (ABC), где (AB = 3), (AC = 4), (angle A=30).
Найти площадь треугольника.
Решение
Для того чтобы найти площадь треугольника, воспользуемся ранее доказанной теоремой.
В формулу (S=frac12ABcdot ACcdotsin A) подставляем записанные выше исходные показатели и производим расчет.
(S=frac12cdot3cdot4cdotsin30^circ=frac12cdot3cdot4cdot0,5=3)
Ответ: (;S=3.;)
Формулы площади треугольника
Докажем теорему о том, что площадь треугольника можно выразить формулой S = pr, где S – площадь треугольника, p – половина периметра, r – радиус вписанной в треугольник окружности.
Задан треугольник АВС, вершины которого соединены отрезками с точкой О, являющейся центром вписанной окружности. Таким образом, треугольник АВС разделяется на три треугольника: AOB, АОС и COB. Площадь каждого из трёх треугольников выражается половиной от произведения стороны на радиус вписанной окружности. Соответственно, площадь треугольника АВС равна сумме площадей трёх составляющих его треугольников:
Таким образом, доказанная формула выражает зависимость треугольника от радиуса вписанной в него окружности. Что и требовалось доказать.
Выразим ещё одну формулу площади треугольника, в которой отражена взаимосвязь площади треугольника с радиусом описанной около него окружности. Для этого необходимо доказать теорему, которая уточняет теорему синусов: если в треугольнике АВС стороны АВ = с, ВС = а, СА = b, то справедливы равенства 
, где R – радиус описанной около АВС окружности.
Для начала определим, какой из углов будет острым. Например, им будет являться угол А. Проведём диаметр окружности через центр в точке О из угла В. Обозначим его BD.
В полученном треугольнике DBC вписанные углы опираются на дугу BC. Поскольку она является общей для них, то можно говорить о равенстве углов А и D, а C – прямой угол. Выразим равенство: а = BC = BD sin A = 2R sin A. Из этого следует, что 
.
При помощи теоремы синусов выразим формулу, которая соответствует теореме: 
.
Из доказанной теоремы вытекают два следствия:
- Для треугольника со сторонами a, b и c формула площади выражается в виде S =abc/4R, где S – площадь треугольника, R – радиус описанной около треугольника окружности.
- Площадь треугольника АВС выражается по формуле S = 2R2sinA sinB sinC, где S – площадь треугольника, R – радиус описанной около треугольника окружности.
В первом случае, если допустить, что угол А является противолежащим стороне a, то sin A = a/2R. Тогда площадь треугольника будет выражаться формулой S = (1/2 bc) sin A. Если подставим в формулу значение sin A , то получим: 
Для доказательства второго следствия воспользуемся ранее доказанной теоремой синусов и формулой из первого следствия. Так, для треугольника АВС справедливо равенство 
Таким образом, a = 2 sinA, b = 2 sinB, c = 2 sinC. Согласно формуле первого следствия, можно выразить формулу площади треугольника АВС:
- Взрослым: Skillbox, Geekbrains, Хекслет, Eduson, XYZ, Яндекс.
- 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
- До 7 класса: Алгоритмика, Кодланд, Реботика.
- Английский: Инглекс, Puzzle, Novakid.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Площадь
- Площадь треугольника
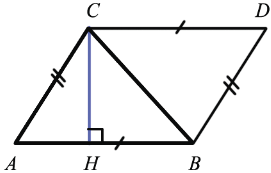
Одну из сторон треугольника часто называют основанием. Если основание выбрано, то под словом «высота» подразумевают высоту треугольника, проведенную к основанию.
Теорема
Площадь треугольника равна половине произведения его основания на высоту
Доказательство
Дано: 
АВС, СН — высота, S — площадь АВС
Доказать: S =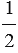 
АВ 
СН
Доказательство:
Достроим данный треугольник до параллелограмма ABCD так, как показано на рисунке. АВС = DCB (по трем сторонам (ВС — общая, AB = CD и АС = BD как противоположные стороны параллелограмма ABCD)), а у равных многоугольников равные площади, значит площади данных треугольников равны. Следовательно, площадь S — площадь АВС равна половине площади параллелограмма ABCD, т.е. S = АВ СН. Теорема доказана.
Следствие 1
Следствие 2
Если высоты двух треугольников равны, то их площади относятся как основания
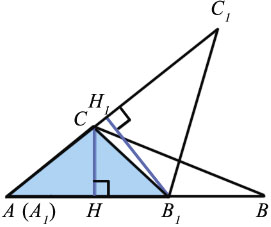
Теорема
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы
Доказательство
Дано: АВС, СН — высота, S — площадь АВС, А1В1С1, В1Н1 — высота, S1 — площадь А1В1С1, 
А = А1
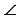
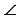
Доказать: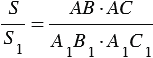 
Доказательство:
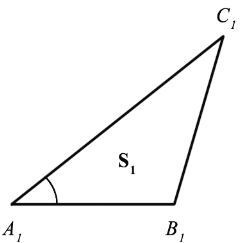
Наложим треугольник А1В1С1 на треугольник АВС так, чтобы вершина А1 совместилась с вершиной А, а стороны А1В1 и А1С1 наложились соответственно на лучи АВ и АС.
Треугольники АВС и АВ1С имеют общую высоту СН, поэтому
Треугольники АВ1С и АВ1С1 также имеют общую высоту — В1Н1, поэтому
Перемножая полученные равенства, находим:
или 
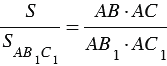
Теорема доказана.
Советуем посмотреть:
Понятие площади многоугольника
Площадь квадрата
Площадь прямоугольника
Площадь параллелограмма
Площадь трапеции
Теорема Пифагора
Теорема, обратная теореме Пифагора
Формула Герона
Площадь
Правило встречается в следующих упражнениях:
7 класс
Задание 490,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 511,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 598,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 619,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 830,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 832,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 846,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1138,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1142,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1304,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник